WSTĘP

W ciągu ostatnich około pięćdziesięciu lat postęp w dziedzinie komputerów i dostępność obrazów w formie cyfrowej umożliwiły ich automatyczne (lub półautomatyczne) przetwarzanie i analizę. Oprócz ogólnego przetwarzania sygnałów, dyscyplina przetwarzania obrazów zyskała ogromne znaczenie zarówno dla zastosowań praktycznych, jak i dla badań teoretycznych. Niektóre ogólne odniesienia do przetwarzania obrazów to: (Castleman, 1979) (Rosenfeld i Kak, 1982) (Jain, 1989) (Pratt, 1991) (Haralick i Shapiro, 1992) (Russ, 2002) (Gonzalez i Woods, 2006). Morfologia matematyczna, której twórcą był Serra i Matheron w latach 60. XX wieku, wyróżnia się spośród innych rodzajów przetwarzania obrazu tym, że między innymi koncentruje się na znaczeniu kształtów. Zasady morfologii matematycznej można znaleźć w licznych publikacjach, takich jak (Serra, 1982) (Serra, 1988) (Giardina i Dougherty, 1988) (Schmitt i Mattioli, 1993) (Maragos i Schafer, 1990) (Heijmans, 1994) (Soille, 2003) (Dougherty i Lotufo, 2003) (Ronse, 2005).

TŁO

Przetwarzanie morfologiczne wykorzystuje w szczególności podejścia oparte na zbiorach, a nie na częstotliwościach. Stanowi to w istocie ostry kontrast z liniowym przetwarzaniem sygnałów , które zajmuje się głównie częstotliwością sygnału wejściowego. Warto również wspomnieć, że morfologia matematyczna (jak sama nazwa wskazuje) zazwyczaj wykorzystuje formalizm matematyczny. Filtrowanie morfologiczne to rodzaj filtrowania obrazu, który koncentruje się na rosnących transformacjach. Kształty mogą być w zadowalający sposób przetwarzane za pomocą filtrów morfologicznych. Zaczynając od elementarnych transformacji opartych na operacjach na zbiorach Minkowskiego, można realizować inne, bardziej złożone transformacje. Teoria filtrowania morfologicznego jest solidnie oparta na matematyce. Niniejszy artykuł przedstawia przegląd filtrowania morfologicznego. Omówiono główne rodziny filtrów morfologicznych, biorąc pod uwagę możliwość obliczania hierarchicznych uproszczeń obrazu. Rozważono zarówno ramy funkcji binarnych (lub zbiorów), jak i ramę funkcji szarości. W dalszej części tej sekcji omówiono podstawowe pojęcia przetwarzania morfologicznego. Skomentowano podstawową strukturę algebraiczną i powiązane z nią operacje, które określają wyróżniające cechy przetwarzania morfologicznego.

PODSTAWOWA STRUKTURA ALGEBRAICZNA I PODSTAWOWE OPERACJE

W przetwarzaniu morfologicznym podstawową strukturą algebraiczną jest krata zupełna . Krata zupełna to zbiór elementów z relacją częściowego uporządkowania, oznaczaną jako ≤, i z dwiema zdefiniowanymi operacjami zwanymi supremum (sup) i infimum (inf):

o Operacja sup oblicza najmniejszy element, który jest większy lub równy operandom. Zatem, jeśli a, b są dwoma elementami kraty, "a sup b" jest elementem kraty, który jest większy zarówno od a, jak i b, i nie ma mniejszego elementu, który byłby większy.
o Operacja inf oblicza największy element, który jest mniejszy lub równy operandom. Ponadto każdy podzbiór kraty ma element infimum i element supremum. Dla zbiorów i obrazów w skali szarości, operacje te to:

o Zbiory (lub obrazy binarne)

o Relacja porządku: ⊆ (zawieranie zbiorów).
o "A sup B" jest równe "A ∪ B", gdzie A i B są zbiorami.
o "A inf B" jest równe "A ∩ B".
o Obrazy w skali szarości (obrazy o wartościach intensywności mieszczących się w zakresie liczb całkowitych)

o Relacja rzędu: Dla dwóch funkcji f, g:

f ≤ g => f(x) ≤ g(x),

dla wszystkich pikseli x, gdzie prawa strona ? odnosi się do relacji rzędu liczb całkowitych.

o Sup funkcji f i g to funkcja:

(f sup g)(x) = max {f(x), g(x)}

gdzie "max" oznacza obliczenie maksymalnej liczby liczb całkowitych.

o Inf funkcji f i g to funkcja: (f inf g)(x) = min {f(x), g(x)}

gdzie "min" symbolizuje obliczenie minimalnej liczby liczb całkowitych.

WŁAŚCIWOŚCI TRANSFORMACJI

Koncepcja uporządkowania jest kluczowa w nieliniowym przetwarzaniu morfologicznym, które koncentruje się szczególnie na transformacjach zachowujących uporządkowanie. Rosnąca transformacja ? zdefiniowana na siatce spełnia, że dla wszystkich a, b:

a ≤ b => Ψ(a) ≤ Ψ(b)

Poniższe dwie właściwości dotyczą uporządkowania między wejściem a wyjściem. Jeśli I oznacza obraz wejściowy, operator obrazu ? jest ekstensywny wtedy i tylko wtedy, gdy ∀I,

I ≤Ψ(I) Powiązaną właściwością jest właściwość anty-ekstensywności. Operator Ψ jest anty-ekstensywny wtedy i tylko wtedy, gdy ∀I,

I ≥Ψ (I)

Koncepcja idempotencji jest fundamentalnym pojęciem w morfologicznym przetwarzaniu obrazów. Operator ? jest idempotentny wtedy i tylko wtedy, gdy ∀I,

Ψ(I) = ΨΨ (I)

W ramach nieliniowej teorii morfologii, ważna zasada dualności głosi, że dla każdego operatora morfologicznego istnieje operator dualny względem operacji dopełnienia. Dwa operatory Ψ iΩ są dualne, jeśli Ψ = CΩ?C. Operacja dopełnienia C, dla zbiorów, oblicza dopełnienie sygnału wejściowego. W przypadku obrazów w skali szarości powiązaną operacją jest inwersja obrazu, która odwraca obraz, odwracając wartości intensywności względem punktu środkowego zakresu wartości intensywności. Poniższa koncepcja piramidy ma zastosowanie do transformacji wieloskalowych. Rodzina operatorów {Ψ_i}, gdzie i ∈ S = {1,…,n}, tworzy piramidę wielopoziomową, jeśli ∀j, k∈? S, j ≥ k, ∃l takie, że Ψ_j = Ψ_l Ψ_k.Innymi słowy, zbiór przekształceń { Ψ_i} tworzy piramidę, jeśli dowolny poziom j hierarchii można osiągnąć, stosując element { Ψ_i} do drobniejszego (o mniejszym indeksie) poziomu k.

ELEMENTY STRUKTURYZUJĄCE

Element strukturalny to podstawowe narzędzie używane przez operatorów morfologicznych do eksploracji i przetwarzania kształtów i form obecnych w obrazie wejściowym. Zazwyczaj stosuje się płaskie elementy strukturalne, które są zestawami definiującymi kształt. Następnie wyświetlane są dwa typowe kształty (kwadrat i romb) (symbol "x" oznacza środek):



Jeśli B oznacza element strukturalny, to jest on transponowany (tj. B odwrócony względem początku układu współrzędnych). Jeśli element strukturalny B jest wyśrodkowany i symetryczny, to ?.

DYLACJE I EROZJE

Dylacje i erozje to najbardziej podstawowe transformacje w przetwarzaniu morfologicznym. Dylacje δ to operatory rosnące, które spełniają równanie ∀I, I′, δ(I sup I′) = δ(I) supδ(I′). Odpowiednio, erozje ε to operatory rosnące, które spełniają równanie ∀I, I′, ε (I inf I′) = ε(I) inf ε(I′).Dylacje i erozje według elementu strukturyzującego wykonują odpowiednio operacje sup i inf na obrazie wejściowym, które zależą od elementu strukturyzującego B. Te dylacje i erozje są symbolizowane odpowiednio przez δ_B i ε_B i wywodzą się z dodawania i odejmowania zbiorów Minkowskiego. Omówmy najpierw strukturę zbiorów. W ramach zbioru, jeśli A oznacza zbiór wejściowy, dylatacja δ_B(A) oblicza zbiór punktów, w których element strukturyzujący B translowany do punktu (lub piksela) A ma niepuste przecięcie (tj. "dotyka"): δ_B(A) = {x | B_x∩ A ≠ Ø?} B_x symbolizuje element strukturyzujący B translowany do punktu (lub piksela) x (tj. B_x = {x′ | x′ - x ∈ B}, gdzie "-" symbolizuje odejmowanie wektorów). Rysunek1 przedstawia przykład zbioru w R².



Zbiór wejściowy A (złożony z dwóch spójnych komponentów) i element strukturyzujący B (koło) są pokazane w części (a). Dylatacja δ_B(A) jest pokazana w części (b). Poprzednie wyrażenie można sformułować za pomocą operacji sup w następujący sposób:



Korzystając z modelu kratowego, wyrażenie dla funkcji jest formalnie identyczne z wyrażeniem dla zbiorów: δ_B(I) = sup_b∈BI_-b Uwaga: operator sup jest operatorem kraty funkcyjnej. Wyrażenie funkcyjne można zapisać w inny sposób, który daje bardziej operacyjne wyrażenie do obliczenia wartości wyniku δ_B(I) dla każdego piksela x zbioru I: [δ_B(I)](x) = max_b∈B{I(x + b)}. Operacja sup została zastąpiona operacją "max", która oblicza maksimum zbioru liczb całkowitych. Należy zauważyć, że "[δ_B(I)](x)" to wartość intensywności piksela x na tym obrazie. Symbol "+" oznacza dodawanie wektorów. Oto kilka ważnych właściwości dylatacji ?_B:

o Dla zbiorów dylatacja ?_B jest przemienna, tj. jeśli A oznacza zbiór wejścowy, to δ_B(A) = δ_A(B).
o Jeśli element strukturalny B zawiera początek układu współrzędnych, to ?_B jest ekstensywny.
o Dylatacja przez element strukturalny jest asocjacyjna, tj. jeśli B jest wynikiem δ_C(D) (lub δ_D(C)), to ?_B(I) = δ_C(δ_D(I)) = δ_D(δ_C(I)). Jeśli A oznacza zbiór wejściowy, a B oznacza element strukturalny, erozja ?B(A) oblicza zbiór punktów, do których translowany element strukturalny B jest w całości zawarty w zbiorze wejściowym A: ε_B(A) = {x | B_x⊆ A}

Rysunek 2 przedstawia przykład zbioru ε_B(A), gdzie A jest przykładem poprzedniego przykładu dylatacji.



Poniższe wyrażenia erozji ε_B są analogiczne do tych wprowadzonych wcześniej dla dylatacji. Wyrażenie dla zbiorów sformułowanych za pomocą operacji inf to:



Wyrażenia dla funkcji to:



Niektóre ważne właściwości erozji ε_B to:

o Jeśli początek układu współrzędnych należy do elementu strukturalnego B, to ε_B jest anty-ekstensywny.

o Erozja przez element strukturalny jest asocjacyjna, tj. jeśli B jest wynikiem δ_C(D) (lub δ_D(C)), to ε_B(I) = ε_C (ε_D(I)) = ε_D (ε_C(I)).

W rzeczywistości wyrażenia dla erozji są dualne w stosunku do, odpowiednio, dylatacji; δ_B i ε_Bsą dualne w stosunku do siebie:

δ_B = C ε_B C

Prosty, jednowymiarowy przykład dylatacji i erozji w skali szarości (gdzie B ma 3 punkty) jest następujący:



OD OPERATORÓW ZBIOROWYCH DO OPERATORÓW FUNKCYJNYCH

Operatorzy płascy to operatory funkcyjne Ψ, które można wyprowadzić z operatora zbiorów Ψ′, spełniające następującą własność superpozycji progowej: [Ψ (I)](x) = sup{u:x ∈ Ψ?′ (U_u(I))}, gdzie U_u jest operatorem progowym na poziomie u, a I jest obrazem. Operator progowy na poziomie u jest zdefiniowany jako U_u(I) = {x : I(x) ≥ u}.Zdefiniujmy wariant operatora progowego, który zwraca funkcję binarną (zamiast zbioru): (U′_u(I))(x) wynosi 1, jeśli I(x)≥ u, i 0 w przeciwnym razie. Następnie operator płaski Ψ, który komutuje z progowaniem, spełnia warunek:

U′_uΨ = ΨU′_u

PODSTAWOWE FILTRY MORFOLOGICZNE

Otwarcia i domknięcia

W przetwarzaniu morfologicznym filtr jest rosnącą i idempotentną transformacją. Dwa najbardziej podstawowe filtry w przetwarzaniu morfologicznym powstają, gdy istnieje porządek między wejściem a wyjściem filtru. Są to tzw. otwarcia i domknięcia, symbolizowane odpowiednio przez γ i Phi;

o Otwarcie γ jest antyekstensywnym filtrem morfologicznym.
o Zamknięcie φ jest ekstensywnym filtrem morfologicznym.

Nazwy "otwarcia algebraiczne" i "domknięcia algebraiczne" są również używane w literaturze w odniesieniu do tych najogólniejszych typów otwarć i domknięć. Następnie omówiono obliczanie otwarć i zamknięć, które wykorzystują elementy strukturalne jako "sondy kształtu" do przetwarzania kształtów obrazu wejściowego. Są one definiowane w kategoriach dylatacji i erozji przez element strukturalny. Dla zbioru wejściowego A, otwarcie przez element strukturalny B, symbolizowane przez γ_B, to zbiór punktów x należących do translowanego elementu strukturalnego, który pasuje do zbioru A, tj. który jest zawarty w A. Ustalmy, jak γ_B jest obliczane w kolejnej definicji, która dotyczy zarówno zbiorów, jak i obrazów. Otwarcie przez element strukturalny B, symbolizowane przez γ_B, jest definiowane przez

γ_B = δ_B ε_B

tj. γ_B to sekwencyjna kompozycja erozji ε_B, po której następuje dylatacja , gdzie ? oznacza transpozycję B. Ten typ filtra najpierw eroduje obraz wejściowy poprzez Erozja ε_B, a następnie następująca dylatacja B, jest definiowany przez



tj. φ_B jest sekwencyjną kompozycją dylatacji δ_B, po której następuje erozja , gdzie ? oznacza transpozycję B.

Filtry naprzemienne

Sekwencyjne kompozycje otwarcia γ i zamknięcia φ nazywane są naprzemiennymi kompozycjami sekwencyjnymi. Morfologiczny filtr naprzemienny to sekwencyjna kompozycja otwarcia i zamknięcia, tj. φγ i γφ są filtrami naprzemiennymi. Ważnym faktem jest to, że generalnie nie ma uporządkowania między wejściem a wyjściem filtrów naprzemiennych, tj.



Ponadto generalnie nie ma uporządkowania między φγ i γφ. Filtry naprzemienne są bardzo przydatne w przetwarzaniu i analizie obrazu, ponieważ w pewien sposób łączą efekty zarówno otwarć, jak i zamknięć w jednym filtrze.

Właściwości kombinacji równoległej

Klasa otwarć (lub odpowiednio zamknięć) jest domknięta na mocy operacji sup (odpowiednio inf). Innymi słowy:

o Nadmiar otworów jest otworem.
o Nadmiar domknięć jest otworem.

Można łączyć różne elementy strukturalne, aby uzyskać pożądany efekt filtrowania kształtu. Na przykład, efekt nadmiaru otworów, takiego jak (γ_A sup γ_B), który sam jest otworem, może znacznie różnić się od efektu γ_A lub γ_B

GRANULOMETRIE I ANTYGRANULOMETRIE

Koncepcja granulometrii formalizuje pojęcie rozkładu wielkości. Rozkłady wielkości to rodziny przekształceń Ψ_i z parametrem rozmiaru i, które spełniają następujące aksjomaty:

o Rosnąco
o Anty-ekstensywność
o Absorpcja

Jeśli Ψ_i, Ψ_j należą do rozkładu wielkości, gdzie i ≤ j, to



W filtrowaniu morfologicznym tak zwane granulometrie to rodziny przekształceń, które spełniają powyższe aksjomaty rozkładu wielkości. Rodzina otworów {γ_i,}, gdzie i ∈ S = {1,…,n} jest granulometrią, jeśli dla każdego i, j ∈ S, i ≤ j => γ_i ≥ γ_j. tj. uporządkowana rodzina otworów stanowi granulometrię. Dualna koncepcja granulometrii nazywana jest anty-granulometrią, która jest uporządkowaną rodziną zamknięć, jak zdefiniowano poniżej. Rodzina domknięć {φ_i}, gdzie i ∈ S = {1,…,n} jest antygranulometrią, jeśli dla każdego i, j ∈ S, i ≤ j => φ_i ≤φ_j. Często oblicza się zarówno granulometrię, jak i antygranulometrię. Zwykle na każdym wyjściu oblicza się ilościowo rosnące miary. Te wartości miar tworzą krzywą, którą można wykorzystać do scharakteryzowania obrazu wejściowego, jeśli kryterium miary jest odpowiednie.



Przykładem kryterium rosnącego jest powierzchnia lub liczba pikseli w obrazach binarnych lub objętość w obrazach niebinarnych. Aby zbudować rodzinę otworów i rodzinę zamknięć poprzez elementy strukturalne, które stanowią odpowiednio granulometrię i antygranulometrię, potrzebna jest odpowiednia rodzina elementów strukturalnych {iB | i ∈ {0,…,N}}, które zapewniają kolejność otworów i zamknięć. W szczególności rodzina elementów strukturalnych musi spełniać następującą właściwość:

γ_(i-1)B(iB) = iB, dla i ≥ 1.

Rysunek 3 ilustruje koncepcję granulometrii.



W częściach (b), (c) i (d) przedstawiono trzy wyjścia otworów, w szczególności wyjścia odpowiadające otworom γ₄, γ₆ i γ₈, gdzie podindeks wskazuje rozmiar elementu strukturalnego . Podindeks i odnosi się do kwadratu o boku 2i+1. Istnieje uporządkowanie między czterema obrazami: część (a) ≥ część (b) ≥ część (c) ≥ część (d).

WIELOPOZIOMOWA FILTRACJA MORFOLOGICZNA

Filtry sekwencyjne naprzemienne

Granulometrie i antygranulometrie pozwalają na budowę filtrów złożonych, składających się z uporządkowanych otwarć i zamknięć. Filtr sekwencyjny naprzemienny ASF to uporządkowana sekwencyjna kompozycja filtrów naprzemiennych φ_jγ_j lub γ_jφ_j, takich jak



gdzie i ≥ j ≥ 1, a γ_i i φ_i należą odpowiednio do granulometrii i antygranulometrii. Filtry sekwencyjne naprzemienne spełniają następującą właściwość absorpcji: jeśli i ≥ j, to



Piramidy morfologiczne

Operatory wielopoziomowe (lub wieloskalowe) to rodziny transformacji zależnych od parametru skali i. W filtrach morfologicznych przypadki spełniające warunek piramidy to:

o granulometrie,
o antygranulometrie i
o filtry sekwencyjne naprzemienne.

TRENDY NA PRZYSZŁOŚĆ

Operatorzy uwzględniający aspekty łączności są aktywnym obszarem badań i pracy w dziedzinie przetwarzania morfologicznego. Łączność łatwo integruje się z ramami filtrowania morfologicznego, wykorzystując koncepcję klasy połączonej (i związane z nią otwarcie) wprowadzoną w (Serra, 1988). Klasa filtrów spójnych , które szczególnie dobrze zachowują kształty, została z powodzeniem wykorzystana w aplikacjach przetwarzania i analizy obrazu. W ostatnich latach pewne typy filtrów spójnych, takie jak tzw. poziomowanie których pochodzenie w ramach zbiorów można prześledzić do , stały się przedmiotem nowych wysiłków badawczych.

WNIOSKI

Niniejszy artykuł podsumowuje filtrowanie morfologiczne, które jakościowo różni się od filtrowania liniowego. Różnice te są wyraźne, gdy do filtrowania morfologicznego podejdzie się analizując leżące u jego podstaw ramy algebraiczne oraz kluczowe znaczenie porządkowania i zwiększania. Filtrowanie morfologiczne zapewnia charakterystyczny rodzaj analizy obrazu, odpowiedni do analizy kształtów. Chociaż pierwotnie filtrowanie morfologiczne było szczególnie związane z przetwarzaniem zbiorów (a wiele koncepcji pierwotnie opiera się na zbiorach), rozszerza się ono na niebinarne funkcje poziomów szarości.

WSTĘP

Niezamawiana poczta komercyjna, znana również jako spam, staje się poważnym problemem dla użytkowników i dostawców Internetu . Wielu badaczy zastosowało techniki uczenia maszynowego w celu usprawnienia wykrywania wiadomości spamowych. Najpopularniejsze są modele Naive Bayes , ale inni autorzy zastosowali maszyny wektorów nośnych (SVM), techniki boostingu i drzewa decyzyjne z imponującymi wynikami. SVM okazał się szczególnie atrakcyjny w tym zastosowaniu, ponieważ jest odporny na szum i obsługuje dużą liczbę funkcji . Błędy w filtrowaniu wiadomości antyspamowych są silnie asymetryczne. W związku z tym fałszywe alarmy lub blokowanie prawidłowych wiadomości są niezwykle kosztowne. Kilku autorów zaproponowało nowe wersje oryginalnego algorytmu SVM, które pomagają zmniejszyć liczbę błędów fałszywie dodatnich . W szczególności zasugerowano, że łączenie nieoptymalnych klasyfikatorów może pomóc w zmniejszeniu wariancji predyktora , a w konsekwencji błędów błędnej klasyfikacji. Aby osiągnąć ten cel, zazwyczaj buduje się różne wersje klasyfikatora poprzez próbkowanie wzorców lub cech . Jednak w naszym zastosowaniu oczekuje się, że agregacja silnych klasyfikatorów pomoże jeszcze bardziej zmniejszyć liczbę błędów fałszywie dodatnich . W niniejszym artykule zajmujemy się problemem redukcji błędów fałszywie dodatnich poprzez łączenie klasyfikatorów opartych na wielu odmiennościach. W tym celu budowana jest różnorodność klasyfikatorów, uwzględniająca odmienności odzwierciedlające różne cechy danych. Odmienności są najpierw osadzane w przestrzeni euklidesowej, gdzie SVM jest dostosowywany dla każdej miary. Następnie klasyfikatory są agregowane z wykorzystaniem strategii głosowania . Proponowana metoda została zastosowana do bazy danych uczenia maszynowego Spam UCI z imponującymi rezultatami.

PONOWNE ROZWAŻENIE PROBLEMU ODMIENNOŚCI

Ważnym krokiem w projektowaniu klasyfikatora jest wybór odpowiedniej odmienności, która odzwierciedla bliskość między obiektami. Wybór odpowiedniej odmienności dla danego problemu nie jest jednak łatwym zadaniem. Każda miara odzwierciedla różne cechy zbioru danych, a żadna odmienność nie przewyższa innych w szerokim zakresie problemów. W tej sekcji krótko omówimy główne różnice między kilkoma odmiennościami, które można zastosować do modelowania bliskości między wiadomościami e-mail. Aby uzyskać głębszy opis i definicje, zobacz na przykład . Odległość euklidesowa ocenia, czy cechy kodyfikujące spam różnią się znacząco między wiadomościami. Ta miara jest wrażliwa na rozmiar wiadomości e-mail. Niepodobieństwo cosinusa odzwierciedla kąt między wiadomościami spamowymi. Wartość jest niezależna od długości wiadomości. Różni się ona znacząco od odległości euklidesowej, gdy dane nie są znormalizowane. Miara korelacji sprawdza, czy cechy kodyfikujące spam zmieniają się w ten sam sposób w różnych wiadomościach e-mail. Miary oparte na korelacji mają tendencję do grupowania próbek, których cechy są liniowo powiązane. Korelacja różni się znacząco od cosinusa, jeśli średnia wektorów reprezentujących wiadomości e-mail jest różna od zera. Ta miara jest zniekształcona przez wartości odstające. Korelacja rang Spearmana pozwala uniknąć tego problemu, obliczając korelację między rangami cech. Innym rodzajem miary korelacji, która pomaga pokonać problem wartości odstających, jest indeks t Kendalla, który jest powiązany z probabilistyczną miarą wzajemnej informacji. Gdy wiadomości e-mail są kodowane w przestrzeniach wielowymiarowych i zaszumionych, wspomniane powyżej odmienności podlegają "klątwie wymiarowości". W związku z tym większość odmienności staje się niemal stała, a różnice między nimi zanikają. Problemu tego można uniknąć, wybierając niewielką liczbę cech przed obliczeniem odmienności.

ŁĄCZENIE KLASYFIKATORÓW OPARTYCH NA ODMIENNOŚCI

W tej sekcji wyjaśnimy, jak można rozszerzyć SVM, aby działał bezpośrednio na podstawie miary odmienności. Następnie zaprezentujemy zespół klasyfikatorów opartych na wielu odmiennościach. Na koniec krótko skomentujemy powiązaną pracę. SVM to potężna technika uczenia maszynowego, która jest w stanie poradzić sobie z danymi o dużej liczbie wymiarów i zaszumionymi danymi. Mimo to oryginalny algorytm SVM nie jest w stanie działać bezpośrednio z macierzy odmienności. Aby rozwiązać ten problem, stosujemy podejście . Najpierw odmienności są osadzane w przestrzeni euklidesowej w taki sposób, że odległości między wzorcami odzwierciedlają w przybliżeniu oryginalną macierz odmienności. Następnie punkty testowe są osadzane za pomocą operacji algebry liniowej, a na koniec SVM jest trenowany i oceniany. Krótko omówimy szczegóły matematyczne. Niech D ∈ R^nxn będzie macierzą odmienności utworzoną z bliskości obiektów dla zbioru treningowego. Konfigurację w niskowymiarowej przestrzeni euklidesowej można znaleźć za pomocą metrycznego algorytmu skalowania wielowymiarowego (MDS) , tak aby pierwotne odmienności były w przybliżeniu zachowane. Niech X = [x₁,…,x_n]^T∈ R^nxp będzie macierzą współrzędnych obiektów dla wzorców treningowych. Zdefiniuj B = X X^T jako macierz iloczynów skalarnych, która jest powiązana z macierzą niepodobieństwa za pomocą następującego równania:

B=-1/2JD⁽²⁾ J(1)

gdzie J = I - 1/n 1 1^T∈ R^nxn to macierz centrująca, I to macierz jednostkowa, a D⁽²⁾ = (δ_ij²) to macierz kwadratowych niepodobieństwa dla wzorców treningowych. Jeśli B jest dodatnio półokreślona, współrzędne obiektu w niskowymiarowej przestrzeni euklidesowej R^k można znaleźć poprzez rozkład na wartości osobliwe:

X_k =V_kA_k^1/2 (2)

gdzie V_k∈ R^nxk jest macierzą ortogonalną, której kolumny stanowią pierwsze k wektorów własnych XX^T, a Λ_k = diag(λ₁ … λ_k) ∈ R^kxk jest macierzą diagonalną, gdzie λ_i jest i-tą wartością własną. Kilka odmienności wprowadzonych w rozdziale 2 generuje macierze iloczynu skalarnego B niesemitycznie określone dodatnie. Na szczęście wartości ujemne są małe w naszym zastosowaniu i dlatego można je pominąć bez utraty istotnych informacji o danych . Po osadzeniu wzorców uczących w niskowymiarowej przestrzeni euklidesowej, wzorzec testowy można dodać do tej przestrzeni za pomocą projekcji liniowej .Następnie krótko skomentujemy wyprowadzenie. Niech X_k ∈ R_nxk będzie konfiguracją obiektu dla wzorców treningowych w R^k, a X_n = [x₁,…,x_s]^T ∈ R^sxk macierzą współrzędnych obiektu poszukiwanych dla wzorców testowych. Niech n⁽²⁾∈ R^sxn będzie macierzą kwadratowych różnic między s wzorcami testowymi a n wzorcami treningowymi, które zostały już rzutowane. Macierz B_n ∈ R^sxn iloczynów skalarnych wzorców testowych i treningowych można znaleźć jako:

B_n =-1/2(D_n²J -UD⁽²⁾J)(3)

gdzie J ?∈ R^nxn jest macierzą centrującą, a U = 1/n1^T1 ∈ R^sxn. Wyprowadzenie równania jest szczegółowo opisane w (Pekalska, 2001). Ponieważ macierz iloczynów skalarnych sprawdza

B_n = X_nX_k^T (4)

wówczas X_n można znaleźć jako rozwiązanie równania (4) o najmniejszym średnim błędzie kwadratowym, czyli:

X_n=B_nX_k(X_k^TX_k)^-1(5)

Biorąc pod uwagę, że X_k^T X_k = Λ_k i X_k = V_k Λ_k^1/2, współrzędne punktów testowych można uzyskać jako:

X_n = B_nV_kΛ_k^-1/2 (6)

co można łatwo oszacować za pomocą prostych liniowych operacji algebraicznych. Proponowana tutaj strategia łączenia opiera się na dowodach, że różne odmienności odzwierciedlają różne cechy zbioru danych. W związku z tym klasyfikatory oparte na różnych miarach będą błędnie klasyfikować inny zestaw wzorców. Rysunek pokazuje na przykład, że pogrubione wzorce są przypisywane do niewłaściwej klasy przez tylko jeden klasyfikator, ale przy użyciu strategii głosowania wzorce zostaną przypisane do właściwej klasy



Zatem nasz algorytm łączenia działa w następujący sposób: Najpierw obliczane są odmienności wprowadzone w sekcji 2. Każda odmienność jest osadzona w przestrzeni euklidesowej, a współrzędne wzorca uczącego i testującego są uzyskiwane odpowiednio za pomocą równań (2) i (6). Aby zwiększyć różnorodność klasyfikatorów, po osadzeniu odmienności losowana jest próbka bootstrapowa wzorców. Następnie trenujemy SVM dla każdej odmienności i próbki bootstrapowej. Oczekuje się zatem, że błędy błędnej klasyfikacji będą się różnić w zależności od klasyfikatora. Zatem połączenie klasyfikatorów za pomocą strategii głosowania pomoże zmniejszyć liczbę błędów błędnej klasyfikacji. Pokrewną techniką łączenia klasyfikatorów jest metoda Bagging . Metoda ta generuje różnorodność klasyfikatorów, które są trenowane z wykorzystaniem kilku próbek bootstrapowych. Następnie klasyfikatory są agregowane z wykorzystaniem strategii głosowania. Niemniej jednak istnieją trzy istotne różnice między metodą bagging a metodą proponowaną w tej sekcji. Po pierwsze, nasza metoda generuje różnorodność klasyfikatorów, uwzględniając różne odmienności, a tym samym indukuje większe zróżnicowanie wśród klasyfikatorów. Drugą zaletą naszej metody jest możliwość bezpośredniej pracy z macierzą odmienności. Wreszcie, połączenie kilku odmienności pozwala uniknąć problemu wyboru konkretnej odmienności dla danej aplikacji. Jest to trudne i czasochłonne zadanie. Należy zauważyć, że algorytm zaproponowany wcześniej można łatwo zastosować do innych klasyfikatorów, takich jak algorytm k najbliższych sąsiadów, opartych na odległościach.

WYNIKI EKSPERYMENTALNE

W tej sekcji zaproponowano zestaw klasyfikatorów do identyfikacji wiadomości spamowych. Rozważany zbiór spamu jest dostępny w bazie danych UCI Machine Learning .Korpus składa się z 4601 wiadomości e-mail, z czego 39,4% to spam, a 60,6% to wiadomości legalne. Liczba cech branych pod uwagę do kodyfikacji wiadomości e-mail wynosi 57 i została opisana w publikacji . Odmienności obliczono bez normalizacji zmiennych, ponieważ może to zwiększyć korelację między nimi. Po osadzeniu odmienności w przestrzeni euklidesowej, zmienne są normalizowane do wariancji jednostkowej i średniej zerowej. To wstępne przetwarzanie poprawia dokładność SVM i szybkość zbieżności. W odniesieniu do zespołu klasyfikatorów, istotną kwestią jest wymiarowość, w której osadzona jest macierz odmienności. W tym celu najpierw uruchamiany jest metryczny algorytm skalowania wielowymiarowego. Liczba rozpatrywanych wektorów własnych jest określana przez krzywą indukowaną przez wartości własne. Dla rozpatrywanego zbioru danych, rysunek 2 pokazuje, że pierwsze dwadzieścia wartości własnych zachowuje główną strukturę zbioru danych.



Strategia kombinacji zaproponowana w niniejszym artykule została również zastosowana do klasyfikatora k najbliższych sąsiadów. Ważnym parametrem tego algorytmu jest liczba sąsiadów, która została oszacowana przy użyciu 20% wzorców jako zbioru walidacyjnego. Klasyfikatory zostały ocenione z dwóch różnych punktów widzenia: z jednej strony obliczyliśmy błędy błędnej klasyfikacji. Jednak w naszej aplikacji błędy fałszywie dodatnie są bardzo kosztowne i należy ich unikać. Dlatego błędy fałszywie dodatnie są również obliczane.Na koniec błędy zostały ocenione z uwzględnieniem podzbioru 20% wzorców wylosowanych losowo bez zwracania z oryginalnego zbioru danych. Tabela przedstawia wyniki eksperymentalne dla zespołu klasyfikatorów z wykorzystaniem SVM.



Proponowaną metodę porównano z metodą baggingu wprowadzoną w rozdziale 3 oraz z klasyfikatorami opartymi na pojedynczej odmienności. Z analizy tabeli 1 można wyciągnąć następujące wnioski:

o Strategia kombinacji znacząco poprawia odległość euklidesową, która jest zazwyczaj uwzględniana przez większość algorytmów SVM.
o Strategia kombinacji z jądrem wielomianowym znacząco redukuje błędy fałszywie dodatnie najlepszego pojedynczego klasyfikatora. Poprawa jest mniejsza w przypadku jądra liniowego. Można to wyjaśnić, ponieważ jądro nieliniowe pozwala nam budować klasyfikatory o większej wariancji, a zatem strategia kombinacji może osiągnąć większą poprawę błędów fałszywie dodatnich. Stwierdzamy również, że w przypadku strategii kombinacji wraz ze wzrostem parametru C błędy fałszywie dodatnie zbiegają się do 0, mimo że liczba błędów fałszywie ujemnych rośnie.
o Proponowana strategia kombinacji przewyższa powszechnie stosowaną metodę agregacji, taką jak Bagging. Ta poprawa jest szczególnie istotna w przypadku jądra wielomianowego.

Tabela 2 przedstawia wyniki eksperymentalne dla zespołu klasyfikatorów k-NN.



Podobnie jak w poprzednim przypadku, proponowana strategia kombinacji poprawia w szczególności błędy fałszywie dodatnie klasyfikatorów opartych na pojedynczej odległości. Stwierdzamy również, że Bagging nie jest w stanie zmniejszyć błędów fałszywie dodatnich dla odległości euklidesowej. Ponadto nasza strategia kombinacji znacznie poprawia algorytm Bagging. Wreszcie obserwujemy, że błędy błędnej klasyfikacji są większe dla k-NN niż dla SVM. Można to wyjaśnić, ponieważ SVM ma większą zdolność generalizacji.

WNIOSKI I PRZYSZŁE TRENDY BADAWCZE

W niniejszym artykule zaproponowaliśmy zespół klasyfikatorów oparty na zróżnicowaniu odmienności. Nasze podejście ma na celu zmniejszenie w szczególności błędów fałszywie dodatnich klasyfikatorów opartych wyłącznie na pojedynczej odległości. Ponadto algorytm może działać bezpośrednio z macierzy odmienności. Algorytm został zastosowany do identyfikacji wiadomości spamowych. Wyniki eksperymentów sugerują, że proponowana metoda pomaga wyeliminować zarówno błędy błędnej klasyfikacji, jak i błędy fałszywie dodatnie. Donosimy również, że nasz algorytm przewyższa klasyfikatory oparte na pojedynczej odmienności i inne strategie łączone, takie jak bagging. W ramach przyszłych trendów badawczych postaramy się zastosować inne strategie łączone, które przypisują każdemu klasyfikatorowi inną wagę.

WSTĘP

Algorytmy genetyczne (GA) to stochastyczne techniki wyszukiwania oparte na koncepcjach naturalnej genetyki populacyjnej, służące do eksploracji ogromnej przestrzeni rozwiązań w celu identyfikacji rozwiązań optymalnych lub zbliżonych do optymalnych . Są one bardziej podatne na uniknięcie problemu lokalnych optimów niż tradycyjne techniki optymalizacji oparte na gradiencie i wspinaczce górskiej przy rozwiązywaniu złożonych problemów. W istocie, algorytmy genetyczne to rodzaj techniki uczenia się przez wzmacnianie , która pozwala na stopniowe ulepszanie rozwiązań na podstawie poprzednich rozwiązań. Algorytmy genetyczne charakteryzują się zdolnością do łączenia potencjalnych rozwiązań w celu efektywnego wykorzystania obiecującego obszaru w przestrzeni rozwiązań, jednocześnie stochastycznie eksplorując nowe obszary wyszukiwania z oczekiwaną poprawą wydajności. Wiele udanych zastosowań tej techniki jest często zgłaszanych w różnych gałęziach przemysłu i przedsiębiorstwach, w tym w optymalizacji funkcji , zarządzaniu ryzykiem finansowym i portfelem , handlu na rynkach , wizji maszynowej i rozpoznawaniu wzorców , wyszukiwaniu dokumentów , projektowaniu topologii sieci , harmonogramowaniu produkcji oraz optymalizacji dynamicznej konfiguracji pamięci systemu operacyjnego , między innymi. W niniejszym badaniu wprowadzamy koncepcję i komponenty algorytmów genetycznych, a następnie stosujemy technikę algorytmów genetycznych do modelowania problemu wyboru partii w elastycznych systemach produkcyjnych (FMS). Model opracowany w tym artykule stanowi podstawę eksperymentu opisanego w Deng.

ALGORYTMY GENETYCZNE

Algorytmy genetyczne to techniki symulacyjne zaproponowane przez Johna Hollanda w latach 60. XX wieku. Zasadniczo algorytmy genetyczne rozwiązują problemy poprzez utrzymywanie i modyfikowanie populacji potencjalnych rozwiązań za pomocą operatorów genetycznych. W trakcie tego procesu korzystne zmiany w rozwiązaniach nadrzędnych są łączone z ich potomkami, tworząc optymalne lub prawie optymalne rozwiązania dla danego zadania. Z natury rzeczy algorytmy genetyczne badają jednocześnie wiele potencjalnie obiecujących obszarów w przestrzeni rozwiązań i losowo przełączają się z jednego obszaru do drugiego w celu poprawy wydajności. Według Hollanda (1992) obszary w przestrzeni rozwiązań można zdefiniować za pomocą składniowych wzorców rozwiązań, a każdy wzorzec nazywany jest schematem. Schemat reprezentuje wzorzec wspólnych atrybutów lub cech rozwiązań w tym samym obszarze. Niech Σ będzie alfabetem symboli. Ciąg znaków nad alfabetem to skończony ciąg symboli z alfabetu. Schemat n-arny jest definiowany jako ciąg znaków w (Σ ∪ {#})ⁿ, gdzie # ∉ Σ jest używane jako oznaczenie wieloznaczne dla dowolnego symbolu w Σ. Koncepcyjnie schematy n-arne można traktować jako definiujące hiperpowierzchnie n-wymiarowego hipersześcianu, który reprezentuje przestrzeń wszystkich rozwiązań n-atrybutowych. Poszczególne rozwiązania w tym samym obszarze można traktować jako instancje schematu reprezentującego, a pojedyncze rozwiązanie może należeć do wielu schematów jednocześnie. W rzeczywistości rozwiązanie n-atrybutowe należy do 2ⁿ różnych schematów. Dlatego ocena rozwiązania ma podobny efekt, jak jednoczesne próbkowanie 2ⁿ obszarów (tj. schematów), co jest słynnym ukrytym paralelizmem przeszukiwania genetycznego. Populacja M rozwiązań będzie zawierać co najmniej 2ⁿ i co najwyżej M ⋅ 2ⁿ schematów. Nawet dla niewielkich wartości n i M, w populacji dostępna będzie duża liczba schematów do przetworzenia. Algorytmy genetyczne wykonują niejawne równoległe przeszukiwanie przestrzeni możliwych schematów w formie jawnego równoległego przeszukiwania przestrzeni pojedynczych rozwiązań. Proces rozwiązywania problemów w algorytmach genetycznych przebiega według pięciofazowego cyklu operacyjnego: generowanie, ocena, selekcja, rekombinacja (lub krzyżowanie) i mutacja. Najpierw generowana jest populacja rozwiązań kandydackich. Następnie definiowana jest funkcja dopasowania lub funkcja celu, a każde rozwiązanie kandydackie w populacji jest oceniane w celu określenia jego wydajności lub dopasowania. Na podstawie względnej wartości dopasowania, dwa rozwiązania kandydackie są wybierane probabilistycznie jako rodzice. Rekombinacja jest następnie stosowana probabilistycznie do dwojga rodziców, tworząc dwoje potomków, a każde z rozwiązań potomnych zawiera pewne cechy z rozwiązań macierzystych. Następnie mutacja jest stosowana oszczędnie do składników każdego rozwiązania potomnego. Nowo wygenerowane potomstwo jest następnie wykorzystywane do zastąpienia członków o niskiej sprawności w populacji. Proces ten jest powtarzany aż do utworzenia nowej populacji. Dzięki powyższym iteracyjnym cyklom operacji, algorytmy genetyczne są w stanie opracowywać lepsze rozwiązania poprzez kolejne generacje. Aby przygotować się do badania efektów operacji genetycznych w ramach dalszych badań, w następnej sekcji zastosujemy technikę algorytmów genetycznych do optymalizacji modelowania systemów produkcyjnych.

SYSTEM WYBORU PARTII OPARTY NA DIAGRAMIE GA

Wybór partii jest jednym z najważniejszych zadań w opracowywaniu głównego planu produkcji dla elastycznych systemów produkcyjnych (FMS). W procesie produkcyjnym każdy produkt wymaga obróbki za pomocą różnych zestawów narzędzi na różnych maszynach, z różnymi operacjami wykonywanymi w określonej kolejności. Każda maszyna ma ograniczoną przestrzeń montażową narzędzi i ograniczony czas przetwarzania. W przypadku różnego rodzaju ograniczeń zasobów, wybór optymalnej partii produktów do produkcji w ciągłym procesie operacyjnym, w celu maksymalizacji wykorzystania maszyn lub zysków, sprawił, że decyzja o wyborze partii stała się bardzo trudnym problemem. Chociaż problem ten jest zazwyczaj możliwy do rozwiązania w przypadku produkcji niewielkiej liczby produktów, szybko staje się nierozwiązywalny, gdy liczba produktów wzrośnie nawet nieznacznie. Czas potrzebny na wyczerpujące rozwiązanie problemu będzie rósł w sposób niedeterministyczny, wielomianowy, wraz z liczbą produktów do wytworzenia. Wybór partii wpływa na wszystkie późniejsze decyzje dotyczące harmonogramowania produkcji w warsztacie, mające na celu realizację głównego planu produkcji, i stanowi klucz do efektywnego wykorzystania zasobów przy tworzeniu planów produkcyjnych w celu realizacji zleceń produkcyjnych. W naszym sformułowaniu używamy następujących symboli denotacyjnych:

o M: liczebność zbioru dostępnych maszyn
o T: liczebność zbioru dostępnych narzędzi
o P: liczebność zbioru produktów do wytworzenia
o Wykorzystanie Maszyny: funkcja całkowitego wykorzystania maszyny
o czas_przetwarzania_{produkt, narzędzie ,maszyna}: czas potrzebny na wytworzenie produktu za pomocą narzędzia narzędzie na maszynie
o dostępny_czas_maszyna: całkowity dostępny czas przetwarzania na maszynie
o pojemność_maszyna: całkowita liczba slotów dostępnych na maszynie
o maszyna, narzędzie, produkt: wskaźniki maszyn, narzędzi i produktów do wytworzenia
o slot_tool: liczba slotów wymagana przez obrabiarkę narzędzie
o ilość_produktu: ilość produktu, która ma zostać wytworzona w jednej zmianie
o Q_produkt: ilość produktu zamówiona przez klientów, zgodnie z tabelą produkcji

Funkcja sprawności (lub celu)

Celem jest identyfikacja partii produktów do wytworzenia w taki sposób, aby zmaksymalizować całkowity wskaźnik wykorzystania maszyny.



Powyższa funkcja celu ma być maksymalizowana przy następujących ograniczeniach zasobów:

1. Ograniczenie wydajności maszyny .



Powyższa funkcja f( •?) służy do określenia, czy narzędzie musi być zamontowane na maszynie w celu przetworzenia bieżącej partii produktu.
2. Ograniczenie czasowe maszyny .



3. Ograniczenia nieujemności i liczby całkowite.

Koder/Dekoder

Koder/Dekoder to schemat reprezentacji używany do określenia struktury problemu w systemie algorytmów genetycznych. Sposób kodowania potencjalnych rozwiązań jest jednym z kluczowych czynników sukcesu algorytmów genetycznych. Ogólnie rzecz biorąc, kodowanie rozwiązania można zdefiniować na alfabecie Σ, który może składać się z cyfr binarnych, liczb ciągłych, liczb całkowitych lub symboli. Jednak wybór najlepszego schematu kodowania jest niemal równoznaczny z rozwiązaniem samego problemu . W niniejszych badaniach nasz system algorytmów genetycznych opiera się głównie na kanonicznym modelu Hollanda , który jest jednym z najczęściej stosowanych w praktyce schematów kodowania - kodowaniem binarnym. Rozwiązaniem kandydackim dla zadania wyboru partii jest wektor ilości, które mają zostać wyprodukowane dla P produktów. Niech cała przestrzeń rozwiązań będzie oznaczona jako rozwiązanie .



Funkcja kodowania koduje ilość, która ma zostać wyprodukowana dla każdego produktu jako l-bitowy ciąg binarny, a następnie tworzy konkatenację ciągów dla P produktów, które mają zostać zawarte w partii produkcyjnej. Każde rozwiązanie kandydackie (ilość₁,…, ilość_P) jest ciągiem o długości lP nad alfabetem binarnym Σ = {0, 1}. Tak zakodowany ciąg l-bitowy ma wartość równą



W powyższym wzorze 2^l - 1 to wartość ciągu l-bitowego ? , a φbull;κ to funkcja sufitowa. Załóżmy na przykład, że w partii produkcyjnej, gdzie 200 sztuk to największa możliwa ilość do wytworzenia dla każdego produktu, należy wybrać tylko dwa produkty. Rozwiązanie kandydackie składające się z ilości 100 i 51 dla produktów 1 i 2 będzie reprezentowane przez 16-bitowy ciąg jako 0110010000110011, przy czym pierwsze 8 bitów reprezentuje produkt 1, a drugie 8 bitów reprezentuje produkt 2. Po wygenerowaniu nowego ciągu rozwiązania jest on dekodowany z powrotem do formatu w celu obliczenia funkcji celu i sprawdzenia wykonalności rozwiązania. Niech każdy l-bitowy segment ciągu rozwiązania będzie oznaczony jako ciąg, gdzie ciąg[i] będzie wartością i-tego bitu w segmencie l-bitowym. Funkcja dekodująca konwertuje każdy ciąg l-bitowy zgodnie z następującym wzorem:



Pięciofazowe operacje genetyczne

Nasz system postępuje zgodnie z cyklami generacji-oceny-selekcji-krzyżowania-mutacji, poszukując odpowiednich ciągów rozwiązań dla zadania selekcji wsadowej. Rozpoczyna od wygenerowania losowo populacji początkowej, Pop, ciągów rozwiązań kandydackich pop_size. W każdej iteracji cyklu operacyjnego każdy ciąg rozwiązań kandydackich, si, w bieżącej populacji jest oceniany przez funkcję dopasowania. Ciągi rozwiązań kandydackich w bieżącej populacji są wybierane probabilistycznie na podstawie ich wartości dopasowania jako zalążki do generowania kolejnego pokolenia. Celem selekcji jest generowanie potomstwa o wysokiej wartości dopasowania na podstawie lepiej dopasowanych członków w bieżącej populacji. W rzeczywistości selekcja jest mechanizmem, który pomaga naszemu systemowi algorytmów genetycznych wykorzystać obiecujący region w przestrzeni rozwiązań. Istnieje kilka schematów selekcji opartych na dopasowaniu: selekcja koła ruletki, selekcja oparta na rangach, selekcja turniejowa i selekcja elitarna . Pierwsze trzy metody losowo wybierają kandydujące ciągi rozwiązań do reprodukcji na podstawie wartości dopasowania lub rangi pojedynczych ciągów. Najlepsi członkowie bieżącej populacji mogą zostać utraconi, jeśli nie zostaną wybrani do reprodukcji lub jeśli zostaną zmienieni przez crossover (tj. rekombinację) lub mutację. Elitarna strategia selekcji ma na celu zachowanie niektórych z najlepiej przystosowanych osobników z bieżącej populacji. Elitarna selekcja zachowuje ograniczoną liczbę "elitarnych" ciągów rozwiązań, tj. ciągów o najlepszych wartościach dopasowania, do przekazania następnemu pokoleniu bez żadnych modyfikacji. Ułamek zwany "przerwą pokoleniową" służy do określenia proporcji populacji, która ma zostać zastąpiona przez ciągi potomne po każdej iteracji. Nasz system GA zachowuje kopie pierwszych "elitarnych" członków populacji Pop w celu utworzenia kolejnej populacji, Pop_new. Aby wygenerować resztę członków dla Pop_new, moduł GA wybierze probabilistycznie:



pary ciągów rozwiązań z Pop do generowania ciągów potomnych. Prawdopodobieństwo wybrania ciągu rozwiązań, s_i, z Pop jest podane wzorem



Niech skumulowane prawdopodobieństwo pojedynczych ciągów rozwiązań w populacji będzie nazywane C_i, a



dla i = 1, 2,…, rozmiar_pow. Ciąg rozwiązań si zostanie wybrany do odtworzenia, jeśli C_i-1 < rand(0,1) ≤ C_i

Oprócz wykorzystania obiecującego obszaru rozwiązań poprzez proces selekcji, musimy również zbadać inne obiecujące obszary w celu znalezienia potencjalnie lepszych rozwiązań. Eksploatacja bez eksploracji spowoduje degenerację populacji ciągów rozwiązań i może spowodować problem lokalnych optimów dla systemu. W rzeczywistości możliwość utrzymania równowagi między eksploatacją a eksploracją jest główną zaletą podejścia algorytmów genetycznych w porównaniu z tradycyjnymi technikami optymalizacji. Funkcja eksploracji jest realizowana przez operatory krzyżowania i mutacji. Te dwa operatory generują rozwiązania potomne, które należą do nowych schematów, a tym samym pozwalają naszemu systemowi badać inne obiecujące obszary w przestrzeni rozwiązań. Ten proces pozwala również naszemu systemowi na stochastyczną poprawę wydajności. Krzyżowanie rekombinuje dobre ciągi rozwiązań w bieżącej populacji i stopniowo rozmnaża populację schematami o wysokiej wartości dopasowania. Krzyżowanie jest powszechnie uważane za najbardziej wyróżniający się operator algorytmów genetycznych i zazwyczaj oddziałuje w bardzo trudny do opanowania sposób z Funkcja dopasowania, kodowanie i inne szczegóły algorytmu genetycznego (Mitchell, 1996). Chociaż zaproponowano różne operatory krzyżowania, nie ma ogólnych wniosków dotyczących tego, kiedy używać którego typu krzyżowania (Michalewicz, 1994) (Mitchell, 1996). W niniejszym artykule przyjmujemy standardowe krzyżowanie jednopunktowe dla naszego systemu algorytmów genetycznych. Dla każdej pary ciągów rozwiązań wybranych do reprodukcji, wartość crossover_rate określa prawdopodobieństwo ich rekombinacji. Pozycja w obu kandydujących ciągach rozwiązań jest losowo wybierana jako punkt krzyżowania. Części dwóch ciągów macierzystych za pozycją krzyżowania są zamieniane, tworząc dwa potomstwo. Niech k będzie punktem krzyżowania wygenerowanym losowo z rozkładu jednostajnego w zakresie od 1 do lP, gdzie lP jest długością ciągu rozwiązań. Niech s_i = (x₁, x₂,…, x_k-1, x_k,…, x_lP) i s_j = (y₁, y₂,…, y_k-1, y_k,…, y_lP) reprezentują parę kandydackich ciągów rozwiązań wybranych do reprodukcji. Na podstawie tych dwóch ciągów operator krzyżowania generuje dwa potomstwa s_i′ = (x₁′, x₂′,…, x_lP′) i s_j′ = (y₁′, y₂′,…, y_lP′) gdzie



Innymi słowy, s′_i = (x₁, x₂,…, x_k-1, y_k, …, y_lP) i s′_j = (y₁, y₂,…, y_k-1, x_k,…, x_lP). Te dwa przeciwstawne sploty są następnie dodawane do Pop_new. Ten proces generowania potomstwa jest powtarzany, aż dla Pop_new zostanie wygenerowane potomstwo o rozmiarze geberation _gap ⋅ pop_size. Dzięki samej selekcji i krzyżowaniu nasz system może czasami wytworzyć jednorodną populację składającą się z tych samych ciągów rozwiązań. To uniemożliwi naszemu systemowi rozpoznanie innych możliwych rozwiązań. Mutacja, która jest drugim operatorem stosowanym w procesie reprodukcji, pomaga naszemu systemowi uniknąć utworzenia jednorodnej populacji poprzez wprowadzenie różnorodności do populacji. Powszechnie uważa się, że sama mutacja nie przyspiesza poszukiwania rozwiązania i jest zazwyczaj uważana za drugorzędną rolę w działaniu algorytmów genetycznych . Zazwyczaj mutacja jest stosowana w celu zmiany wartości bitowej ciągu w populacji tylko sporadycznie. Niech mutation_rate będzie prawdopodobieństwem mutacji dla każdego bitu w kandydującym ciągu rozwiązań. Dla każdego ciągu potomnego, s′ = (x′₁,x′₂,…,x′_lp wygenerowanego przez operator krzyżowania dla nowej populacji Pop_new, operator mutacji odwróci każdy bit probabilistycznie:



Prawdopodobieństwo mutacji dla kandydującego ciągu rozwiązań wynosi 1- 1(mutatiot_rate)^lP ? Powyższe procesy stanowią cykl operacyjny naszego systemu. Operacje te są powtarzane aż do osiągnięcia kryterium zakończenia, a wynik jest przekazywany do dekodera w celu zdekodowania. Zdekodowany wynik jest następnie przedstawiany decydentowi do dalszego rozważenia w ostatecznej decyzji. Jeśli bieżące rozwiązanie nie jest satysfakcjonujące dla decydenta, może je zmodyfikować, a następnie wprowadzić do systemu algorytmów genetycznych w celu zainicjowania kolejnego przebiegu procesu wyszukiwania satysfakcjonujących rozwiązań.

PRZYSZŁE TRENDY I WNIOSKI

W niniejszym artykule zaprojektowaliśmy system oparty na algorytmach genetycznych dla problemu wyboru partii w elastycznych systemach produkcyjnych. W naszym projekcie przyjęliśmy schemat kodowania binarnego, elitarną strategię wyboru, strategię krzyżowania jednopunktowego i jednolitą mutację losową dla problemu wyboru partii. Na wydajność algorytmów genetycznych zwykle wpływają różne parametry i skomplikowane interakcje między nimi, a istnieje kilka kwestii wartych dalszego zbadania. Dzięki dostępności większej puli zróżnicowanych schematów w większej populacji, nasz algorytm genetyczny System będzie miał szerszy widok na "krajobraz" przestrzeni rozwiązań i dlatego jest bardziej prawdopodobne, że będzie zawierał reprezentatywne rozwiązania z dużej liczby hiperpłaszczyzn. Ta zaleta daje algorytmom genetycznym większe szanse na odkrycie lepszych rozwiązań w przestrzeni rozwiązań. Jednakże Davis (1991) twierdzi, że najbardziej efektywny rozmiar populacji zależy od charakteru problemu, formalizmu reprezentacji i operatorów algorytmów genetycznych. Mimo to Schaffer i inni stwierdzili, że najlepsze ustawienia rozmiaru populacji są niezależne od problemów. W dalszej części tego artykułu przeprowadzimy serię eksperymentów, aby systematycznie analizować wpływ rozmiaru populacji na wydajność algorytmów genetycznych, wykorzystując model wyboru partii przedstawiony w tym artykule, abyśmy mogli być bardziej decyzyjni w kwestii efektywnego rozmiaru populacji.

WSTĘP

Tradycyjnie techniki obliczeń ewolucyjnych (EC), a konkretnie algorytmy genetyczne (GA) , okazały się skuteczne w rozwiązywaniu różnych problemów; jednakże, potencjalnym problemem algorytmów genetycznych jest to, że zazwyczaj dostarczają one unikalnego rozwiązania dla problemu, do którego są stosowane. Niektóre rozwiązania nieglobalne odrzucone podczas poszukiwania najlepszego mogą być akceptowalne w pewnych okolicznościach. Większość problemów w świecie rzeczywistym obejmuje przestrzeń poszukiwań z jednym lub wieloma rozwiązaniami globalnymi i wieloma rozwiązaniami lokalnymi; oznacza to, że są to problemy multimodalne , a zatem, jeśli chcemy uzyskać wiele rozwiązań za pomocą algorytmów genetycznych, konieczna byłaby modyfikacja ich klasycznego schematu działania w celu ich prawidłowego dostosowania do multimodalności takich problemów.

MOTYWACJA

Tupodjęto próbę scharakteryzowania problemów multimodalnych. Podjęto również próbę przedstawienia globalnego spojrzenia na niektóre z kilku proponowanych podejść do adaptacji klasycznego funkcjonowania algorytmów genetycznych do poszukiwania wielu rozwiązań. Na koniec przedstawiono również wkład autorów.

TŁO: CHARAKTERYSTYKA PROBLEMÓW WIELOMODALNYCH

Problemy multimodalne można w skrócie zdefiniować jako problemy, które mają wiele optimum globalnego lub wiele optimum lokalnego. W przypadku tego typu problemów interesujące jest uzyskanie jak największej liczby rozwiązań z kilku powodów. Z jednej strony, gdy nie ma pełnej wiedzy o problemie, uzyskane rozwiązanie może nie być najlepsze, ponieważ nie można stwierdzić, że nie można znaleźć lepszego rozwiązania w przestrzeni poszukiwań, która nie została jeszcze zbadana. Z drugiej strony, pomimo pewności, że uzyskano najlepsze rozwiązanie, mogą istnieć inne, równie dopasowane lub nieco gorsze rozwiązania, które mogą być preferowane ze względu na różne czynniki (łatwiejsze zastosowanie, prostszą interpretację itp.) i dlatego uważane za globalnie lepsze. Jedną z najbardziej charakterystycznych funkcji multimodalnych wykorzystywanych w problemach laboratoryjnych jest funkcja Rastrigina (patrz rysune. 1), która oferuje doskonały graficzny punkt widzenia na temat średnich multimodalnych.



Podanie wielu optymalnych (i poprawnych) rozwiązań, a nie tylko jednego, unikalnego rozwiązania globalnego, ma kluczowe znaczenie w środowiskach wielowymiarowych. Zazwyczaj wdrożenie w praktyce najlepszego rozwiązania jest bardzo skomplikowane, co może wiązać się z wieloma problemami: zbyt wysokim kosztem obliczeniowym, złożoną interpretacją… W takich sytuacjach przydatne okazuje się posiadanie szeregu prawidłowych rozwiązań, spośród których można wybrać takie, które - mimo że nie jest najlepszym rozwiązaniem problemu - oferuje akceptowalny poziom dostosowania i jest prostsze do wdrożenia, zrozumienia… niż idealne rozwiązanie globalne.

TECHNIKI EWOLUCYJNE I PROBLEMY WIELOMODALNE

Jak wspomniano, zastosowanie technik EC do rozwiązywania problemów multimodalnych niesie ze sobą trudności, jakie stwarzają tego typu techniki, ponieważ zazwyczaj dostarczają one jedynie najlepsze z znalezionych rozwiązań i odrzucają możliwe lokalne optimum, które mogły zostać znalezione w trakcie poszukiwań. W tradycyjnym działaniu algorytmu genetycznego wprowadzono wiele modyfikacji, aby osiągnąć dobre wyniki w przypadku problemów multimodalnych. Kluczowym aspektem przy uzyskiwaniu wielu rozwiązań jest zachowanie różnorodności populacji genetycznej, a także maksymalne rozproszenie osobników genetycznych w przestrzeni poszukiwań.

PODEJŚCIA KLASYCZNE

Metody niszowania pozwalają algorytmom genetycznym utrzymać populację genetyczną zróżnicowanych osobników, dzięki czemu możliwe jest znalezienie wielu optymalnych rozwiązań w obrębie jednej populacji. Aby zminimalizować wpływ homogenizacji lub zapobiec jej wpływowi jedynie na późniejsze etapy fazy poszukiwań, opracowano kilka alternatyw, opartych większość z nich na heurystyce. Jedną z pierwszych alternatyw promujących różnorodność było zastosowanie metod skalowania do populacji w celu podkreślenia różnic między poszczególnymi osobnikami. Inną bezpośrednią drogą do uniknięcia utraty różnorodności jest skupienie się na eliminacji zduplikowanych częściowych rozwiązań o wysokim dopasowaniu . Niektóre inne podejścia próbują rozwiązać ten problem za pomocą dynamicznej zmienności współczynników krzyżowania i mutacji . Większa liczba mutacji jest przeprowadzana w celu zwiększenia eksploracji przestrzeni poszukiwań, gdy różnorodność maleje; mutacje maleją, a krzyżowania rosną, aby poprawić wykorzystanie w poszukiwaniu optymalnych rozwiązań, gdy różnorodność rośnie. Istnieją również propozycje nowych operatorów genetycznych lub wariantów istniejących. Na przykład niektóre z algorytmów krzyżowania, które zwiększają różnorodność i które należy wyróżnić, to BLX (Blend Crossover) , SBX (Simulated Binary Crossover) , PCX (Parent Centric Crossover), CIXL2 (Confidence Interval Based Crossover using L2 Norm) lub UNDX (Unimodal Normally Distributed Crossover).W odniesieniu do algorytmów zastępowania, poszukiwano również schematów, które mogłyby zachować różnorodność populacji. Przykładem tego typu schematów jest tłumienie . W tym przypadku nowo utworzony osobnik jest porównywany z losowo wybranym podzbiorem populacji, a osobnik najbardziej zbliżony do niego jest wybierany do zastąpienia. Techniki zagęszczania są inspirowane naturą, gdzie podobni członkowie populacji naturalnych konkurują o ograniczone zasoby. Podobnie, różne osobniki zazwyczaj zajmują różne nisze i jest mało prawdopodobne, aby konkurowały o ten sam zasób, dlatego oferowane są różne rozwiązania. Współdzielenie sprawności zostało po raz pierwszy wdrożone przez Goldberga i Richardsona do zastosowania w funkcjach multimodalnych . Podstawowa koncepcja polega na określeniu, na podstawie sprawności każdego rozwiązania, maksymalnej liczby osobników, które mogą pozostać wokół niego, nagradzając osobniki wykorzystujące unikalne obszary domeny. Dynamiczne współdzielenie sprawności z dwoma składnikami zostało zaproponowane w celu skorygowania rozproszenia ostatecznego rozkładu osobników w niszach: funkcji odległości, która mierzy nakładanie się osobników, oraz funkcji porównania, która daje wynik "1", jeśli osobniki są identyczne, a wartości są bliższe "0", im bardziej się różnią. Metoda oczyszczania znacznie różni się od poprzednich, ponieważ zasoby nie są współdzielone, lecz przydzielane najlepszym jednostkom, które następnie są utrzymywane w każdej niszy. Główną wadą opisanych wcześniej technik jest to, że dodają one nowe parametry, które należy skonfigurować zgodnie z procesem wykonywania algorytmu genetycznego. Proces ten może być zakłócony przez interakcje między tymi parametrami.

WŁASNE PROPOZYCJE

Po wykryciu istniejących problemów należy je rozwiązać lub przynajmniej zminimalizować. W tym celu grupa zajmująca się sztucznymi sieciami neuronowymi i systemami adaptacyjnymi (RNASA) opracowała dwie propozycje wykorzystujące techniki EC do tego typu problemów. Obie propozycje starają się znaleźć rozwiązanie końcowe, ale zachowując rozwiązania cząstkowe w populacji końcowej. Główne idee obu propozycji, wraz z problemami użytymi w testach, wyjaśniono w poniższych punktach.

Hybrydowy algorytm genetyczny dla dwóch populacji

Wprowadzenie

Aby wymusić jednorodne przeszukiwanie w całej przestrzeni przeszukiwania, proponowane tutaj podejście opiera się na dodaniu nowej populacji (puli genetycznej) do tradycyjnej GA (populacji wtórnej). Pula genetyczna podzieli przestrzeń przeszukiwania na podregiony. Każdy z osobników puli genetycznej ma swój własny, ogrodzony zakres zmienności genów, więc każdy z tych osobników reprezentowałby określony podregion w globalnej przestrzeni przeszukiwania. Z drugiej strony, grupa zakresów indywidualnych, w których dowolny gen może mieć swoją wartość, jest rozciągnięta na całość możliwych wartości, jakie może mieć gen. Dlatego ta pula genetyczna obejmowałaby całą przestrzeń poszukiwań. Należy pamiętać, że tradycyjny algorytm genetyczny (GA) przeprowadza swoje poszukiwania, biorąc pod uwagę tylko jeden podregion (całą przestrzeń poszukiwań). W tym przypadku przestrzeń poszukiwań zostanie podzielona na różne podregiony lub przedziały w zależności od liczby osobników genetycznych w puli genetycznej. Ponieważ osobniki w puli genetycznej mają wartości restrykcyjne w swoich wartościach genów żywotnych, żaden z tych osobników nie otrzyma prawidłowego rozwiązania. Dlatego też, oprócz puli genetycznej, wykorzystuje się również inną populację (populację wtórną). W tym przypadku klasyczny algorytm genetyczny rozwijałby swoje osobniki w sposób interaktywny z osobnikami z puli genetycznej. W przeciwieństwie do puli genetycznej, geny osobników z populacji wtórnej mogą przyjmować wartości w całej przestrzeni poszukiwań, więc wnosiłyby wkład w rozwiązania, podczas gdy pula genetyczna działałaby jako wsparcie, utrzymując przestrzeń poszukiwań jednorodnie eksplorowaną. Populacja wtórna dostarczy rozwiązań (ponieważ jej osobniki mogą się zmieniać w całym zakresie przestrzeni poszukiwań), natomiast pula genetyczna będzie działać jako wsparcie, utrzymując przestrzeń poszukiwań jednorodnie eksplorowaną. Następnie obie populacje, przedstawione graficznie na rysunku 2, zostaną szczegółowo opisane.



Pula genetyczna

Jak wspomniano wcześniej, każdy osobnik w puli genetycznej reprezentuje podregion globalnej przestrzeni poszukiwań. Dlatego powinien mieć taką samą strukturę lub sekwencję genów, jak w przypadku tradycyjnego GA. Różnica polega na zakresie wartości, jakie mogą mieć te geny. Przy oferowaniu rozwiązania, tradycyjne GA może mieć dowolną prawidłową wartość, podczas gdy w proponowanym GA zakres możliwych wartości jest ograniczony. Całkowity zakres wartości jest dzielony na taką samą liczbę części, co liczba osobników w puli genetycznej, tak aby każdemu osobnikowi przydzielony był podzakres wartości. Wartości, które dany gen może mieć, pozostaną w swoim zakresie przez cały czas działania proponowanego GA. Oprócz tego, co zostało powiedziane, każdy osobnik w puli genetycznej będzie decydował o tym, które geny odpowiadają najlepszemu dotychczasowemu rozwiązaniu (czyli czy należą do najlepszego osobnika w populacji wtórnej). Ta wartość boolowska byłaby wykorzystywana w celu uniknięcia modyfikacji tych genów, które w danej fazie działania stanowią najlepsze rozwiązanie problemu. Co więcej, każdy z genów u danego osobnika ma przypisaną wartość I, która wskazuje względny przyrost, jaki zostałby zastosowany do genu podczas operacji mutacji opartej wyłącznie na przyrostach i stosowanej wyłącznie do osobników z puli genetycznej. Oczywiste jest, że ta wartość przyrostu powinna być niższa niż maksymalny zakres, w którym wartości genów mogą się zmieniać. Strukturę osobników w puli genetycznej przedstawiono na rysunku 3.



Ponieważ osobniki te nie reprezentują globalnych rozwiązań problemu, który należy rozwiązać, ich wartość dopasowania nie będzie obowiązkowa. Zmniejszy to złożoność algorytmu i, oczywiście, zwiększy wydajność obliczeniową ostatecznej implementacji.

Populacja wtórna

Osoby populacji wtórnej znacznie różnią się od populacji poprzedniej. W tym przypadku geny osobników populacji wtórnej mogą przyjmować dowolną wartość w całej przestrzeni możliwych rozwiązań. Dzięki temu wszystkie osobniki populacji wtórnej mogą oferować globalne rozwiązania problemu. Nie jest to możliwe w puli genetycznej, ponieważ ich geny są ograniczone do różnych podzakresów. Ewolucja osobników w puli genetycznej będzie prowadzona zgodnie z tradycyjnymi zasadami algorytmów genetycznych. Główna różnica polega na operatorze krzyżowania. W tym przypadku zostanie zastosowana zmodyfikowana metoda krzyżowania. Ponieważ informacja jest przechowywana w izolowanej populacji, dwoje rodziców, którzy dadzą nowe potomstwo, nie będzie należało do tej samej populacji. W związku z tym pula genetyczna i populacja wtórna zostaną połączone. W ten sposób informacje z obu populacji zostaną połączone, aby uzyskać najlepiej dopasowane potomstwo.

Operator krzyżowania

Jak wspomniano wcześniej, operator krzyżowania rekombinuje materiał genetyczny osobników obu populacji. Rekombinacja ta obejmuje losowego osobnika z populacji wtórnej z przedstawicielem puli genetycznej. Ten przedstawiciel będzie reprezentował potencjalne rozwiązanie oferowane przez pulę genetyczną. Ponieważ unikatowy osobnik nie może spełnić tego wymogu, przedstawiciel zostanie utworzony z podzbioru genów różnych osobników z puli genetycznej. Zebranie informacji z różnych rozwiązań cząstkowych pozwoli na wygenerowanie prawidłowego rozwiązania globalnego. Zatem wartość dla każdego genu przedstawiciela zostanie losowo wybrana spośród wszystkich osobników w puli genetycznej. Po przypisaniu wartości wszystkim genom, ten nowy osobnik nie będzie reprezentował rozwiązania cząstkowego, w przeciwieństwie do każdego osobnika z osobna, lecz rozwiązania globalnego. Teraz zostanie zastosowany operator krzyżowania. Ta funkcja krzyżowania zachowa różnorodność populacji wtórnej, więc potomstwo będzie zawierało wartości z puli genetycznej. W związku z tym algorytm genetyczny będzie mógł utrzymać wiele rozwiązań w tej samej populacji. Operator krzyżowania nie zmienia puli genetycznej, ponieważ ostatni działa jedynie jako silnik utrzymujący różnorodność. Proces ten podsumowano na rysunku 4.



Operator mutacji

Operator mutacji zwiększa wartość poszczególnych genów w puli genetycznej. Wprowadza nowe informacje do puli genetycznej, aby przedstawiciel mógł je wykorzystać, a następnie, za pomocą operatora krzyżowania, wprowadza je do populacji wtórnej. Należy zauważyć, że nowa wartość będzie miała górny limit, więc po jej osiągnięciu nowa wartość genu zostanie zresetowana do wartości dolnej. Wraz z postępem pokoleń wartość przyrostu jest zmniejszana, więc przyrost zastosowany do osobników w puli genetycznej będzie przyjmował niższe wartości. Różne przyrosty między iteracjami są obliczane z uwzględnieniem dolnej wartości genu (LIM_INF_IND), górnej wartości tego genu (LIM_SUP_IND) oraz całkowitej liczby osobników w puli genetycznej (IND_POOL), jak podsumowano na rysunku 5.



W ten sposób pierwsze pokolenia będą pobieżnie badać przestrzeń poszukiwań (przeszukiwanie zgrubne), a celem jest przeprowadzenie bardziej wyczerpującego przeglądu wszystkich wartości, jakie może posiadać dany gen (przeszukiwanie precyzyjne) w miarę postępu procesu wyszukiwania.

Algorytm genetyczny z podziałem na gatunki

Innym proponowanym rozwiązaniem jest adaptacja techniki niszowania (nitching). Polega ona na podziale populacji genetycznej na różne i niezależne podgatunki. W tym przypadku kryterium determinujące przynależność konkretnego osobnika do konkretnego gatunku jest ustalane na podstawie podobieństwa genotypów (podobne genotypy tworzą izolowane gatunki). Ta klasyczna koncepcja została wzbogacona o pewne udoskonalenia, aby nie tylko zmniejszyć liczbę iteracji potrzebnych do uzyskania rozwiązań, ale także zwiększyć liczbę rozwiązań przechowywanych w populacji genetycznej. Kilka iteracji algorytmu genetycznego zostało wykonanych dla każdego gatunku w populacji genetycznej, aby przyspieszyć konwergencję w kierunku rozwiązania, które istnieje w pobliżu każdego gatunku. Osobniki wygenerowane podczas tej operacji, posiadające genotyp innego gatunku, zostaną odrzucone. Operacje krzyżowania między gatunkami są następnie stosowane podobnie jak w biologii. Z jednej strony preferowane są krzyżowania między podobnymi osobnikami (jak to miało miejsce w poprzednim kroku z wykorzystaniem algorytmów genetycznych), a z drugiej strony krzyżowania między różnymi gatunkami są możliwe, choć w mniejszym stopniu.Osobniki wygenerowane po tych krzyżowaniach mogłyby zostać włączone do już istniejącego gatunku lub, jeśli analizują nowy obszar przestrzeni poszukiwań, stworzyć sobie nowy gatunek. Ostatecznie algorytm genetyczny dostarcza tyle rozwiązań, ile gatunków pozostaje aktywnych w przestrzeni poszukiwań.

TRENDY NA PRZYSZŁOŚĆ

Ponieważ nie ma metod, które dawałyby najlepsze wyniki we wszystkich możliwych sytuacjach, opracowywane byłyby nowe podejścia. Nowe funkcje dopasowania pomogłyby zlokalizować dużą liczbę prawidłowych rozwiązań w przestrzeni poszukiwań. W opisanych podejściach funkcja ta pozostaje stała podczas wykonywania metody. Inną opcją byłoby dopuszczenie dynamicznych funkcji dopasowania, które zmieniają się w trakcie wykonywania. Tego rodzaju funkcje będą próbowały dostosować swoje wyniki do wiedzy uzyskanej z przestrzeni poszukiwań, podczas gdy operatory krzyżowania i mutacji eksplorują nowe obszary. Jeśli różne techniki oferują akceptowalne rozwiązania, inne interesujące podejście polega na ich łączeniu. Na przykład, takie modele hybrydowe integrowałyby metody statystyczne (z bogatym zapleczem matematycznym) z innymi heurystykami.

WNIOSKI

Niniejszy artykuł przedstawia przegląd różnych metod związanych z technikami ewolucyjnymi, stosowanych w rozwiązywaniu problemu multimodalności. W rozdziale tym przedstawiono kilka podejść, które pozwalają na dostarczenie nie tylko globalnego rozwiązania, ale wielu rozwiązań tego samego problemu. Pomogłoby to użytkownikowi końcowemu zdecydować, które z nich jest najodpowiedniejsze w danym przypadku. Ostateczna decyzja będzie zależeć od kilku czynników, nie tylko od globalnego błędu osiągniętego dla danej metody. Inne czynniki zależą również od wpływu ekonomicznego,trudności wdrożenia, jakości wiedzy dostarczonej do analizy itd.

WSTĘP

Aby dostosować dane wejściowe i zadania użytkowników, system interaktywny musi być w stanie ustalić zbiór założeń dotyczących profili użytkowników i charakterystyki zadań, które często określa się mianem modeli użytkownika. Jednak, aby opracować model użytkownika, system interaktywny musi analizować dane wejściowe użytkowników oraz rozpoznawać zadania i ostateczne cele, które użytkownicy próbują osiągnąć, co może wiązać się z dużą ilością niepewności. W tym rozdziale omówiono i przeanalizowano podejścia do radzenia sobie z niepewnością. Celem jest przedstawienie analitycznego przeglądu i perspektywy dotyczącej głównych metod proponowanych w celu radzenia sobie z niepewnością.

Podejścia do radzenia sobie z niepewnością

Przez długi czas model bayesowski był podstawowym numerycznym podejściem do reprezentacji i wnioskowania z niepewnością. Zaproponowano również kilka modeli matematycznych, różniących się od modelu prospektywnego probabilistycznego. Głównymi z nich są teoria dowodowa (funkcja przekonań) Shafera-Dempstera oraz teoria możliwości Zadeha. Podejmowano również próby rozwiązania problemu niekompletnej informacji za pomocą logiki klasycznej. Zaproponowano wiele podejść do logiki wnioskowania domyślnego, a badania nad logiką niemonotoniczną zyskały duże zainteresowanie. Podejścia te można podzielić na dwie kategorie: podejścia numeryczne i podejścia nienumeryczne.

1. Rachunek prawdopodobieństwa i teoria bayesowska. Istnieją dowody na teoretyczną konieczność i uzasadnienie stosowania modelu probabilistycznego do reprezentacji wiedzy, łączenia i propagacji dowodów, zdolności uczenia się i jasności wyjaśnień . Przetwarzanie bayesowskie pozostaje podstawową ideą leżącą u podstaw wielu nowych propozycji, które rzekomo mają skutecznie radzić sobie z niepewnością.We wszystkich dotychczasowych osiągnięciach praktycznych wzór bayesowski i wartości prawdopodobieństwa były wykorzystywane jako pewnego rodzaju współczynniki rozszerzające wiedzę deterministyczną reprezentowaną przez reguły produkcji (Barr i Feigenbaum, 1982). Zaproponowano i zastosowano pewne intuicyjne metody łączenia i propagacji tych wartości. Jednym z takich przypadków jest zastosowanie współczynników pewności (CF) w MYCIN (Shortliffe i Buchanan, 1976). Rich również stosuje uproszczone podejście CF w systemie modelowania użytkowników GROUNDY . Pojawiły się jednak pewne zastrzeżenia wobec takich probabilistycznych metod uwzględniania niepewności (Karnal i Lemmer, 1986). Jednym z głównych zastrzeżeń jest brak określonej semantyki tych wartości ze względu na sposób ich wykorzystania. Użycie pojedynczej liczby do podsumowania informacji o niepewności zawsze było kwestią sporną . Podejście bayesowskie wymaga, aby każdy dowód był warunkowo niezależny. Stwierdzono, że założenia warunkowej niezależności dowodów w ramach hipotez są sprzeczne z innymi założeniami wyczerpującej i wzajemnie wykluczającej się przestrzeni hipotez. W szczególności Pednault i inni(1981) pokazują, że przy tych założeniach mogłaby nastąpić probabilistyczna aktualizacja, gdyby istniały więcej niż dwie konkurujące hipotezy. Pearl (1985) sugeruje, że założenie warunkowej niezależności dowodów w ramach negacji hipotez jest zbyt restrykcyjne. Na przykład, jeśli proces wnioskowania zawiera wiele ścieżek łączących dowody z tą samą hipotezą, niezależność jest naruszona. Podobnie, wymagana wzajemna wykluczalność i wyczerpujący charakter hipotez nie są zbyt realistyczne. To założenie nie byłoby spełnione, gdyby jednocześnie wystąpiło więcej niż jedna hipoteza i jest tak restrykcyjne, jak założenie o jednym domyślnym założeniu najprostszych systemów diagnostycznych. To założenie wymaga również, aby każda możliwa hipoteza była znana a priori. Zostałoby ono naruszone, gdyby dziedzina problemu nie odpowiadała założeniu świata zamkniętego. Być może najbardziej restrykcyjnym ograniczeniem podejścia Byesa jest jego niezdolność do reprezentowania niewiedzy. Bayesowskie ujęcie prawdopodobieństwa nie pozwala odróżnić niepewności od niewiedzy. Nie można stwierdzić, czy stopień przekonania został bezpośrednio obliczony na podstawie dowodów, czy pośrednio wywnioskowany z braku dowodów. Ponadto metoda ta wymaga dużej ilości danych do określenia oszacowań prawdopodobieństw a priori i prawdopodobieństw warunkowych. Takie wymaganie staje się wykonalne dopiero wtedy, gdy problem można przedstawić jako rzadką sieć bayesowską utworzoną z hierarchii małych skupisk węzłów. W takim przypadku znane są zależności między zmiennymi (węzłami w sieci) i konieczne jest uzyskanie jedynie jawnie wymaganych prawdopodobieństw warunkowych

2. Teoria dowodowa Dempstera-Shafera. Teoria Dempstera-Shafera, zaproponowana przez Shafera , została opracowana w ramach prac Dempstera nad prawdopodobieństwami górnymi i dolnymi indukowanymi przez odwzorowanie wielowartościowe . Podobnie jak teoria bayesowska, teoria ta opiera się na stopniach przekonania, aby przedstawić niepewność. Pozwala ona jednak na przypisanie stopnia przekonania podzbiorom hipotez. Zgodnie z teorią Dempstera-Shafera, cecha odwzorowania wielowartościowego jest fundamentalną przyczyną niemożności zastosowania znanego twierdzenia o prawdopodobieństwie, które określa gęstość prawdopodobieństwa obrazu odwzorowania jeden do jednego . W tym kontekście dolne prawdopodobieństwo jest powiązane ze stopniem przekonania, a górne prawdopodobieństwo ze stopniem prawdopodobieństwa. Ten formalizm definiuje pewność jako funkcję, która odwzorowuje podzbiory przestrzeni zdań na skali [0,1]. Zbiory częściowych przekonań są reprezentowane przez rozkłady mas jednostki przekonania w przestrzeni zdań. Te rozkłady nazywane są podstawowym przyporządkowaniem prawdopodobieństwa. Całkowita pewność w przestrzeni wynosi 1. Można nadać całej przestrzeni zdań niezerowy BPA, aby reprezentować stopień niewiedzy. Pewność dowolnego zdania jest następnie reprezentowana przez przedział charakteryzowany przez prawdopodobieństwo górne i dolne. Reguła kombinacji Dempstera normalizuje przecięcie się korpusów dowodów z dwóch źródeł przez ilość niesprzecznych dowodów między źródłami. Teoria ta jest atrakcyjna z kilku powodów. Po pierwsze, opiera się na klasycznej teorii prawdopodobieństwa, dziedzicząc w ten sposób znaczną część jej podstaw teoretycznych. Po drugie, wydaje się, że nie jest zbyt wymagająca, nie narzucając precyzyjnych sformułowań prawdopodobieństw: jej prawdopodobieństwa nie wydają się dostarczać więcej informacji, niż jest faktycznie dostępne. Po trzecie, odzwierciedla stopień niewiedzy na temat oszacowania prawdopodobieństwa. Po czwarte, teoria Dempstera-Shafera dostarcza reguł łączenia prawdopodobieństw, a tym samym propagacji miar w systemie. Jest to również jeden z najbardziej kontrowersyjnych punktów, ponieważ metoda propagacji jest rozszerzeniem reguły mnożenia dla zdarzeń niezależnych. Ponieważ wiele zastosowań obejmuje zdarzenia zależne, reguła ta może być niemożliwa do zastosowania według klasycznych kryteriów statystycznych. Tendencja do zakładania, że zdarzenia są niezależne, dopóki nie zostanie udowodnione inaczej, wywołała znaczną część krytyki podejść probabilistycznych. Teoria Dempstera-Shafera boryka się z tym samym problemem . Ponadto istnieją dwa problemy z podejściem Dempstera-Shafera. Pierwszym problemem jest złożoność obliczeniowa. W ogólnym przypadku ocena stopnia przekonania i prawdopodobieństwa górnego wymaga czasu wykładniczego w kardynalności zbioru hipotez. Ta złożoność wynika z konieczności enumeracji wszystkich podzbiorów danego zbioru. Drugi problem w tym podejściu wynika z procesu normalizacji przedstawionego zarówno w pracach Dempstera, jak i Shafera. Zadeh argumentował, że ten proces normalizacji może prowadzić do niepoprawnych i kontrintuicyjnych wyników . Usunięcie sprzecznych części dowodów i normalizacja pozostałych części może prowadzić do odrzucenia istotnych informacji zamiast ich odpowiedniego wykorzystania. Dubois i Prade (1985) wykazali również, że proces normalizacji w regułach łączenia dowodów stwarza problem wrażliwości, gdzie przypisanie wartości zerowej lub bardzo małej wartości podstawowemu przypisaniu prawdopodobieństwa powoduje bardzo zróżnicowane wyniki. Opierając się na teorii Dempstera-Shafera, Garvey i inni (1982) zaproponowali podejście zwane rozumowaniem dowodowym, które przyjmuje dowodową interpretację stopnia przekonania i prawdopodobieństw górnych. To podejście definiuje prawdopodobieństwo tezy jako podprzedział przedziału jednostkowego [0,1]. Dolna granica tego przedziału to stopień poparcia tezy, a górna granica to stopień jej prawdopodobieństwa. W przypadku konieczności połączenia odrębnych zbiorów dowodów, podejście to wykorzystuje te same techniki Dempstera-Shafera, wymagające tego samego procesu normalizacji, który był krytykowany przez Zadeha .

3. Zbiory rozmyte i teoria możliwości. Teoria możliwości została zaproponowana niezależnie przez Zadeha, jako rozwinięcie teorii zbiorów rozmytych, w celu radzenia sobie z nieostrością inherentną niektórym terminom językowym . Dla danego zbioru hipotez rozkład możliwości można zdefiniować w sposób bardzo podobny do rozkładu prawdopodobieństwa. Istnieje jednak jakościowa różnica między prawdopodobieństwem a możliwością zdarzenia. Różnica polega na tym, że wysoki stopień prawdopodobieństwa nie implikuje wysokiego stopnia prawdopodobieństwa, ani niski stopień prawdopodobieństwa nie implikuje niskiego stopnia prawdopodobieństwa. Jednakże zdarzenie niemożliwe musi być również nieprawdopodobne. Bardziej formalnie, Zadeh zdefiniował pojęcie rozkładu możliwości. Pojęcie teorii możliwości zostało zbudowane na teorii zbiorów rozmytych i dobrze nadaje się do reprezentowania nieprecyzyjności niejasnych predykatów językowych. Niejasny predykat indukuje zbiór rozmyty i odpowiadający mu rozkład możliwości. Z semantycznego punktu widzenia wartości ograniczone rozkładem możliwości to mniej więcej wszystkie dopuszczalne wartości zmiennej językowej. Teoria ta jest w pełni wykonalna dla każdego elementu uniwersum dyskursu.

4. Teoria potwierdzenia. Cohen (Cohen, 1983) zaproponował inne podejście do reprezentacji niepewności, oparte na jakościowej teorii "potwierdzenia". Według Cohena zapisy czynników związanych z pewnością danej osoby nazywane są potwierdzeniami. Model potwierdzenia Cohena opiera się na jawnym rejestrowaniu uzasadnień stwierdzenia, co zazwyczaj wymaga złożonej struktury danych o źródle. Dlatego takie podejście utrzymuje niepewność. Uzasadnienie jest klasyfikowane według rodzaju dowodów na poparcie tezy, możliwych działań wymaganych do rozwiązania niepewności tych dowodów i innych powiązanych cech. Potwierdzenia mogą stanowić dobry mechanizm wyjaśniania rozumowania, ponieważ tworzą i przechowują całą historię uzasadnień (tj. powody uznania lub odrzucenia tezy) oraz istotność każdej tezy w odniesieniu do danego celu. Potwierdzenia dzielą się na pięć klas: reguły, dane, zadanie, wniosek i rozwiązanie. Cohen wskazuje, że główną różnicą między podejściami numerycznymi a podejściem opartym na potwierdzeniu, szczególnie w odniesieniu do łańcuchów wnioskowania, jest to, że rozumowanie w pierwszym podejściu jest całkowicie automatyczne i nierefleksyjne, podczas gdy drugie podejście dostarcza więcej informacji do wnioskowania o niepewności. W konsekwencji, rozumowanie w drugim podejściu może być kontrolowane i determinowane przez jakość i dostępność dowodów. Potwierdzenia dostarczają informacji niezbędnych do wielu aspektów wnioskowania o niepewności. Potwierdzenia służą do planowania pewnych zadań przed niepewnymi, do selekcji zadań przed ich uruchomieniem, do określania, czy twierdzenie jest wystarczająco pewne dla danego celu, oraz do sugerowania nowych zadań, gdy stare nie radzą sobie z niepewnością. Potwierdzenia rozróżniają różne rodzaje niepewności i dostosowują rozumowanie do tego, co wiadomo na temat niepewności. Jednak Bonissone i Tong (1995) argumentują, że kombinacje potwierdzeń w przesłance (tj. twierdzeniu), propagacja potwierdzeń do wniosku i ranking potwierdzeń muszą być wyraźnie określone dla każdego konkretnego kontekstu. Stwarza to potencjalne problemy kombinatoryczne.

5. Rozumowanie oparte na założeniach i logika niemonotoniczna: W podejściu opartym na uzasadnionych założeniach, zaproponowanym przez Doyle′a (1979), niepewność wpisana w regułę implikacji jest usuwana poprzez wyszczególnienie wszystkich wyjątków od tej reguły. Gdy nie jest to możliwe, założenia służą do wykazania typowości wartości (tj. wartości domyślnych) i wykonalności reguły (tj. podatności na obalenie rozumu). W logice klasycznej, jeśli zdanie C można wyprowadzić ze zbioru zdań S, a S jest podzbiorem T, to C również można wyprowadzić z T. Wraz ze wzrostem przesłanek systemu, jego możliwe wnioski pozostają stałe, a bardziej prawdopodobne jest, że rosną. Systemy dedukcyjne o tej właściwości nazywane są monotonicznymi. Tego rodzaju logika nie dysponuje narzędziami opisującymi, jak zrewidować teorię formalną w celu radzenia sobie z niespójnościami spowodowanymi przez nowe informacje. McDermott i Dole zaproponowali niemonotoniczną logikę, aby poradzić sobie z tym problemem .

Gdy założenie zastosowane w procesie dedukcyjnym okaże się fałszywe, konieczne jest zastosowanie mechanizmów niemonotonicznych w celu zachowania integralności stwierdzeń . Jednakże takie podejście nie oferuje możliwości obliczania stopnia przekonania. Bonissone i Tong (1995) sugerują, że systemy oparte na założeniach radzą sobie z przypadkami niekompletnych informacji, ale nie są w stanie poradzić sobie z informacjami nieprecyzyjnymi. W szczególności nie potrafią zintegrować miar probabilistycznych z uzasadnionymi założeniami. Co więcej, takie systemy opierają się na precyzji wartości domyślnych. Z drugiej strony, gdy brakuje konkretnych informacji, system powinien być w stanie wykorzystać analogiczne lub istotne informacje odziedziczone z jakiegoś wyższego poziomu koncepcji. Ten surogat brakujących informacji jest zazwyczaj niejasny lub nieprecyzyjny i zapewnia ograniczone ograniczenia co do wartości brakujących informacji. W systemie wnioskowania wykorzystującym logikę niemonotoniczną przyjmowane są założenia, które mogą wymagać rewizji w świetle nowych informacji. Mają one tę właściwość, że na dowolnym etapie wnioskowania można wyprowadzić więcej niż jeden wzajemnie spójny zbiór wniosków z dostępnych danych i możliwych założeń. Takie wnioski mogą zostać unieważnione, ponieważ nowe dane zostaną uznane za niezgodne z pewnymi domyślnymi założeniami. System wnioskowania wymaga, aby uzasadnienia każdego wniosku były rejestrowane w trakcie procesu wnioskowania i wykorzystywane do cofania się w zależności podczas rewizji przekonań. Jest to realizowane przez System Utrzymywania Prawdy (TMS) .Słabością logiki niemonotonicznej jest to, że w standardowej logice niemonotonicznej jedynym komunikatem przekazywanym przez sprzeczność jest to, że informacja, którą wcześniej uważano za prawdziwą, jest w rzeczywistości fałszywa (na razie). Jednak rzeczywista treść odkrywanej niespójności może nie być tak wiarygodna, jak zakładano, lub może się zdarzyć, że podmiot nie znajduje się w stanie uporządkowanym, lub może być mieszaniną obu tych stanów . Ponadto, ponieważ TMS analizuje nowe informacje pojedynczo, nie jest w stanie wykryć szumu wejściowego, który powinien zostać zignorowany. Ta słabość jest kluczowa dla rozpoznawania wzorców .

WNIOSKI

Tu przeanalizowano podejścia do radzenia sobie z nimi w adaptacyjnym interfejsie człowiek-komputer. Każde podejście może skutecznie poradzić sobie tylko z określonym typem problemów niepewności. System interfejsu wymaga bardziej kompleksowego podejścia do zarządzania niepewnością ze względu na różnorodne źródła niepewności w dialogu człowiek-maszyna. W szczególności, ponieważ dialog człowiek-maszyna jest zazwyczaj zależny od kontekstu, zarządzanie niepewnością musi zapewnić widok sformatowany według wzorca do modelowania użytkownika. Innymi słowy, system modelowania użytkownika musi analizować dane wejściowe użytkownika w oparciu o kontekst dialogu, aby uzyskać kompletne i spójne profile użytkowników. Zaproponowano pewne niekonwencjonalne podejścia do radzenia sobie z niepewnością w systemach interaktywnych, takich jak sieci neuronowe i algorytmy generyczne, ponieważ charakteryzują się one silną zdolnością do rozpoznawania i klasyfikowania wzorców. Jednak konwersja między nienumerycznymi danymi wprowadzanymi przez użytkownika a danymi numerycznymi w celu przetwarzania w sieciach neuronowych nadal wiąże się z wieloma niepewnościami.

WSTĘP

"Uczenie maszynowe (ML) to poddziedzina sztucznej inteligencji, której śmiałym celem jest opracowanie metod obliczeniowych, które implementowałyby różne formy uczenia się, w szczególności mechanizmów zdolnych do indukowania wiedzy z przykładów lub danych" . Najprostszym i najlepiej poznanym zadaniem ML jest uczenie nadzorowane. W uczeniu nadzorowanym każdy przykład składa się z wektora cech (x) i klasy (y). Celem algorytmu uczenia jest, przy danym zbiorze przykładów i ich klas, znalezienie funkcji f, którą można zastosować do przypisania odpowiedniej klasy nowym przykładom. Gdy funkcja f przyjmuje wartości z dyskretnego zbioru klas {C₁, … , C_K,}, f nazywa się klasyfikatorem. W ostatnich dekadach udowodniono, że w zadaniach uczenia się, w których nieznana funkcja f przyjmuje więcej niż dwie wartości (wieloklasowe problemy uczenia się), lepszym podejściem jest dekompozycja problemu na wiele dwuklasowych problemów klasyfikacji . Niniejszy artykuł opisuje implementację systemu, którego głównym zadaniem jest klasyfikacja znaków zakazu na kilka kategorii. Aby zmniejszyć złożoność problemu uczenia się i poprawić wydajność klasyfikacji, system składa się ze zbioru (zespołu) niezależnych klasyfikatorów binarnych. W proponowanym podejściu każdy klasyfikator binarny jest jednowyjściową siecią neuronową (NN) wytrenowaną w celu odróżniania określonego rodzaju znaku drogowego od innych. Proponowany system jest częścią Systemu Wsparcia Kierowcy (DSS) wspieranego przez rząd Hiszpanii w ramach projektu TRA2004-07441-C03-C02. Z tego powodu jednym z głównych wymagań systemowych jest jego implementacja sprzętowa, aby można było go używać w pojeździe do kategoryzacji w czasie rzeczywistym. Aby spełnić to ograniczenie, należy zredukować liczbę cech opisujących instancje. W konsekwencji, jeśli mamy k generycznych typów znaków drogowych, użyjemy k binarnych sieci neuronowych i zostanie wykonany proces selekcji k cech.

WSTĘP

Wiadomo, że znaki drogowe niosą ze sobą istotne informacje dla bezpiecznej jazdy. Między innymi zezwalają lub zabraniają wykonywania określonych manewrów, ostrzegają o czynnikach ryzyka, wyznaczają ograniczenia prędkości oraz dostarczają informacji o kierunkach, miejscach docelowych itp. Dlatego rozpoznawanie znaków drogowych jest kluczowym zadaniem dla rozwoju autonomicznego systemu wspomagania kierowcy. Pomimo rosnącego zainteresowania w ostatnich latach, rozpoznawanie znaków drogowych jest jednym z mniej zbadanych tematów w dziedzinie inteligentnych systemów transportowych. Podejścia w tym obszarze koncentrowały się głównie na rozwiązywaniu innych problemów, takich jak detekcja granic dróg lub rozpoznawanie przeszkód na drodze pojazdu, takich jak piesi lub inne pojazdy . W przypadku dużej liczby typów znaków drogowych, zadanie rozpoznawania znaków drogowych jest rozdzielone na dwa procesy: detekcję i klasyfikację. Proces detekcji odpowiada za lokalizację i ekstrakcję potencjalnych znaków z obrazów rejestrowanych przez kamery. Dopiero po wykryciu potencjalnych znaków można je zaklasyfikować jako jeden z dostępnych typów znaków drogowych. W opublikowanych badaniach detekcja opiera się na kolorze i/lub kształcie znaków drogowych . Z drugiej strony, do rozwiązania problemu klasyfikacji wykorzystano kilka algorytmów uczenia maszynowego. Wśród zastosowanych technik warto wymienić: Model Markowa , Sztuczne Sieci Neuronowe , Metodę Partycjonowania Pierścienia , Filtr Poszukiwania Dopasowania czy klasyfikator jądra Laplace′a .

SYSTEM ROZPOZNAWANIA ZNAKÓW DROGOWYCH OPARTY NA SIECI NEURONOWEJ

W niniejszej pracy przedstawiamy architekturę systemu, którego zadaniem jest klasyfikacja znaków zakazu na kilka kategorii. Zadanie to można opisać jako problem uczenia nadzorowanego, w którym informacje wejściowe pochodzą ze zbioru znaków drogowych uporządkowanych w ustaloną liczbę kategorii (klas), a celem jest wydobycie z danych wejściowych rzeczywistej wiedzy potrzebnej do prawidłowej klasyfikacji nowych znaków. Proponowany system to klasyfikator oparty na perceptronie wielowarstwowym (MLP) i wytrenowany algorytmem propagacji wstecznej (Back-Propagation). Aby zintegrować ten system klasyfikacji z systemem DSS zdolnym do kategoryzacji znaków drogowych w czasie rzeczywistym, niezbędna jest implementacja sprzętowa na układach FPGA (Field Programmable Gate Array). W celu zmniejszenia złożoności problemu zaproponowano zespół wyspecjalizowanych sieci neuronowych. Ponadto, ze względu na ścisłe ograniczenia rozmiaru implementacji sieci neuronowych (ANN) na układach FPGA, konstrukcja każdego wyspecjalizowanego modelu MLP jest połączona ze specyficzną redukcją liczby cech opisujących przykłady.

Wstępne przetwarzanie znaków drogowych

Ponieważ znaki drogowe, które mają zostać sklasyfikowane, są zawarte w obrazach rejestrowanych przez kamerę przymocowaną do poruszającego się pojazdu, można założyć, że znaki mają zmienny rozmiar (znaki stają się większe w miarę zbliżania się pojazdu). Dlatego po wykryciu znaków drogowych pierwszym krokiem jest ich normalizacja do określonego rozmiaru. Celem tego procesu jest zapewnienie, że wszystkie znaki (przykłady) są opisane tą samą liczbą pikseli (cech). W naszym podejściu użyliśmy znaków o wymiarach 32x32 piksele. Po normalizacji znaków przeprowadzana jest konwersja do skali szarości. Ponieważ oryginalne obrazy są reprezentowane w przestrzeni kolorów RGB (czerwony, zielony i niebieski), konwersja ta odbywa się poprzez zsumowanie wartości czerwieni, zieleni i błękitu dla każdego piksela i podzielenie wyniku przez trzy. W wyniku obu procesów każdy znak drogowy jest przekształcany w wektor 1024-elementowy, w którym każdy piksel jest reprezentowany przez liczbę rzeczywistą z zakresu [0,0; 1,0].

Architektura systemu

Ogólna struktura proponowanego systemu składa się z dwóch modułów: modułu wstępnego przetwarzania danych (DPM) i modułu klasyfikacji (CLM).



Funkcją modułu DPM jest wybranie spośród 1024 atrybutów opisujących znak podzbioru, który musi otrzymać każda wyspecjalizowana sieć neuronowa w module CLM. Z drugiej strony, funkcją modułu CLM jest klasyfikowanie każdego zestawu danych wejściowych jako jednego z dostępnych typów znaków zakazu. Ponieważ moduł ten składa się z kilku niezależnych klasyfikatorów, w celu uzyskania ostatecznej klasyfikacji wymagana jest integracja poszczególnych predykcji. Do zbudowania zarówno modułu DPM, jak i modułu CLM niezbędny jest nowy schemat kodowania danych. W szczególności problem wieloklasowy musi zostać rozłożony na zbiór binarnych podproblemów.

Moduł wstępnego przetwarzania danych Doświadczenie praktyczne pokazuje, że wykorzystanie jak największej ilości informacji wejściowych (cech) nie przekłada się na wyższą dokładność wyników. Selekcja podzbioru cech to procedura polegająca na wyborze tylko istotnych informacji, unikaniu informacji nieistotnych i zbędnych oraz redukcji wymiarowości zadania uczenia się. Proponowana architektura przyjmuje model, w którym podzbiór cech opisujący przykład nie jest unikatowy, lecz zależy od zadania związanego z każdym klasyfikatorem. Innymi słowy, ponieważ problem klasyfikacji jest podzielony na k podproblemów binarnych, potrzebnych jest k procedur selekcji cech. W niniejszej pracy moduł selekcji cech został zbudowany z wykorzystaniem narzędzia Weka . Początkowo rozważono kilka algorytmów selekcji cech spośród tych zawartych w Weka . Po przeanalizowaniu zarówno rozmiaru zestawu cech, jak i wyników eksperymentów, jako podstawę konstrukcji modelu DPM wybrano kombinację metody "najlepszy pierwszy" oraz metody selekcji cech opartej na korelacji

Moduł klasyfikacji

Moduł klasyfikacji oparty jest na modelu "jeden przeciw wszystkim" (OAA). W tym modelowaniu, ostateczny klasyfikator składa się ze zbioru klasyfikatorów binarnych, z których każdy specjalizuje się w odróżnianiu określonego typu znaku drogowego od pozostałych. Dlatego w przypadku problemu klasyfikacji, w którym należy rozdzielić k typów znaków drogowych, takie podejście prowadzi do systemu, w którym dla każdej istniejącej klasy używany jest inny NN. Rozłożenie globalnego klasyfikatora na zbiór niezależnych NN nie tylko zmniejsza złożoność problemu, ale także pozwala programowi DPM wybrać najbardziej znaczący zestaw atrybutów dla każdego zadania klasyfikacji binarnej. Ponadto, każdy NN może mieć własną architekturę (liczbę ukrytych węzłów, funkcję aktywacji, szybkość uczenia itp.), a ponieważ nie ma połączenia między poszczególnymi sieciami, uczenie można przeprowadzić, rozdzielając pracę na kilka procesorów.

Kombinacja wyników SNN

Po wytrenowaniu binarnych NN można wygenerować globalny system klasyfikatorów. Ponieważ jednak każdy klasyfikator tworzy własną predykcję, wymagany jest moduł decyzyjny, który integruje wyniki z zestawu klasyfikatorów i generuje unikalną klasyfikację końcową. Eksperymentalnie stwierdzono, że dla proponowanego zadania klasyfikacyjnego najskuteczniejszym kryterium decyzyjnym jest wybór sieci neuronowej o najwyższej wartości wyjściowej. Dlatego wzór użyty w module decyzyjnym jest następujący:



gdzie f_i jest wartością wyjściową sieci neuronowej powiązanej z i-tą klasą.

Proces klasyfikacji

Gdy system odbiera nieoznakowany znak drogowy, który ma zostać sklasyfikowany w jednej ze stałych kategorii, znak ten jest wysyłany do modułu wejściowego każdego klasyfikatora. DPM wybiera podzbiór pikseli zgodnie z odpowiednią listą atrybutów. Wybrane piksele są wykorzystywane jako dane wejściowe dla powiązanej sieci neuronowej (ANN), która wykorzystuje swoją wiedzę do tworzenia predykcji. Poszczególne predykcje są wysyłane do modułu decyzyjnego, który przeprowadza integrację otrzymanych informacji i generuje unikalną klasyfikację końcową. Proces ten przedstawiono na rysunku .



Ewaluacja empiryczna

Proponowany system został zweryfikowany na ponad 5000 przykładach, uporządkowanych w dziesięciu rodzajach znaków zakazu: zakaz ruchu pieszych, zakaz skrętu w lewo/prawo, zakaz zatrzymywania się i parkowania, zakaz wyprzedzania oraz ograniczenia prędkości 20-30-40-50-60 i 100 km/h. Aby ocenić nasze podejście, porównano trzy metody klasyfikacji:

o Bezpośrednie podejście wieloklasowe,
o Podejście OAA z pełną przestrzenią cech oraz
o Podejście OAA z selekcją cech.

W bezpośrednim podejściu wieloklasowym (eksperyment 1) problem klasyfikacji rozwiązano za pomocą MLP z 1024 (32 × 32) węzłami wejściowymi, jedną warstwą ukrytą z 50 neuronami i jedną warstwą wyjściową z 10 neuronami. W tym podejściu klasa powiązana z każdym wzorcem uczącym się jest kodowana za pomocą wektora C, który ma tyle samo składowych ci, ile istnieje klasa (10). Wartość składowej ci będzie wynosić 1, jeśli znak należy do klasy i, i 0 w każdym innym przypadku. W podejściu OAA z pełną przestrzenią cech (eksperyment 2) poprzednia sieć jest podzielona na dziesięć binarnych sieci neuronowych (SSN). Innymi słowy, to podejście wykorzystuje 10 binarnych MLP z 1024 węzłami wejściowymi, 36 węzłami ukrytymi i 1 węzłem wyjściowym. Wreszcie, w podejściu OAA z selekcją cech (eksperyment 3), problem rozwiązano za pomocą zespołu zawierającego 10 binarnych MLP z 36 ukrytymi węzłami w każdym. Liczba jednostek wejściowych, a tym samym przestrzeń cech używana przez każdą sieć neuronową, jest określana przez DPM. Liczba ta jest przedstawiona w Tabeli .



Aby zbudować klasyfikatory binarne używane w dwóch ostatnich eksperymentach, konieczny jest nowy schemat kodowania klas. W obu przypadkach klasa powiązana z każdym wzorcem jest kodowana za pomocą bitu. Ponieważ w obu eksperymentach i-ty klasyfikator binarny jest trenowany w celu odróżnienia klasy i od wszystkich pozostałych klas, nowe kodowanie jest równoważne z wyborem składnika ci z poprzedniej kodyfikacji. W Tabeli 2 przedstawiono oszacowaną dokładność klasyfikacji dla opisanych eksperymentów, gdy zastosowano 10-krotny proces walidacji krzyżowej.



Ocena eksperymentalna pokazuje, że podział zadania klasyfikacji na binarne podzadania (eksperyment 2) zwiększa dokładność klasyfikacji. Z drugiej strony, utrata dokładności klasyfikacji w przypadku przeprowadzenia procesu selekcji cech (eksperyment 3) nie jest zbyt znacząca w porównaniu z korzyściami wynikającymi ze znacznej redukcji danych wejściowych.

PRZYSZŁE TRENDY

Przyszłe prace będą koncentrować się głównie na rozbudowie systemu w celu obsługi znaków regulacyjnych, ostrzegawczych, sygnalizacyjnych itp., tj. z wykorzystaniem większej liczby klas. Zadanie to pozwoli nam zbadać i opracować nowe procedury, które przyczynią się do zaprojektowania bardziej wszechstronnego systemu. W projekcie tego nowego systemu zostaną przeanalizowane inne podejścia wieloklasowe, takie jak modelowanie One Against Higher Order oraz kod wyjściowy korekcji błędów (Error-Correction Output Code) .

WNIOSKI

W niniejszej pracy opisano architekturę klasyfikacji znaków drogowych. Implementacja programowa charakteryzuje się bardzo wysokim wskaźnikiem rozpoznawania. Z tego powodu architekturę tę można uznać za dobre rozwiązanie problemu klasyfikacji znaków drogowych. Ponadto, cechy tej architektury umożliwiają implementację tego systemu na układach FPGA, a tym samym wykorzystanie go w aplikacjach czasu rzeczywistego.

WSTĘP

Wiele organizacji obecnie opracowało własne bazy danych, w których przechowywana jest duża ilość cennych informacji, np. profile osobiste klientów. Informacje te odgrywają ważną rolę w procesach rozwoju organizacji, ponieważ mogą pomóc im lepiej zrozumieć potrzeby klientów. Aby skutecznie wyodrębnić te informacje i zidentyfikować ukryte zależności, konieczne jest zastosowanie inteligentnych technik, na przykład eksploracji danych. Eksploracja danych to proces odkrywania wiedzy . Istnieje szeroki wachlarz technik eksploracji danych, a jedną z nich są drzewa decyzyjne. Drzewa decyzyjne, które mogą być wykorzystywane do celów klasyfikacji i predykcji, są narzędziem wspomagającym podejmowanie decyzji. Ponieważ drzewo decyzyjne może precyzyjnie klasyfikować dane i formułować skuteczne predykcje, zostało już wykorzystane do analizy danych w wielu dziedzinach. W niniejszym artykule staramy się przedstawić przegląd zastosowań, które mogą wspierać drzewa decyzyjne. W szczególności koncentrujemy się na zarządzaniu przedsiębiorstwem, inżynierii i zarządzaniu opieką zdrowotną. Struktura artykułu jest następująca. Po pierwsze, Sekcja 2 przedstawia teoretyczne podstawy drzew decyzyjnych. Sekcja 3 omawia następnie zastosowania, które drzewa decyzyjne mogą wspierać, ze szczególnym uwzględnieniem zarządzania przedsiębiorstwem, inżynierii i zarządzania opieką zdrowotną. Dla każdego zastosowania opisano, w jaki sposób drzewa decyzyjne mogą pomóc w identyfikacji ukrytych relacji. Następnie, Sekcja 4 zawiera krytyczną dyskusję na temat ograniczeń i wskazuje potencjalne kierunki przyszłych badań. Na koniec, Sekcja 5 przedstawia wnioski z artykułu.

TŁO

Drzewa decyzyjne są jednym z najczęściej stosowanych narzędzi klasyfikacji i predykcji. Wynika to prawdopodobnie z faktu, że wiedza odkryta przez drzewo decyzyjne jest zilustrowana w strukturze hierarchicznej, dzięki czemu odkryta wiedza może być łatwo zrozumiana przez osoby, nawet jeśli nie są ekspertami w dziedzinie eksploracji danych . Model drzewa decyzyjnego można utworzyć na kilka sposobów, wykorzystując istniejące algorytmy drzew decyzyjnych. Aby skutecznie wdrożyć takie algorytmy, konieczne jest gruntowne zrozumienie procesów tworzenia modelu drzewa decyzyjnego oraz identyfikacja adekwatności zastosowanych algorytmów drzewa decyzyjnego. Kwestie te opisano w poniższych podsekcjach.

Procesy rozwoju modelu

Powszechnym sposobem tworzenia modelu drzewa decyzyjnego jest zastosowanie podejścia odgórnego, rekurencyjnego oraz dziel i zwyciężaj. Takie podejście modelowania pozwala na umieszczenie najistotniejszego atrybutu na najwyższym poziomie jako węzła głównego, a najmniej istotnych atrybutów na najniższym poziomie jako węzłów opuszczających . Każdą ścieżkę między węzłem głównym a węzłem opuszczającym można interpretować jako regułę "jeśli-to", która może być wykorzystywana do formułowania predykcji . Aby stworzyć model drzewa decyzyjnego w oparciu o powyższe podejście, procesy modelowania można podzielić na trzy etapy: (1) wzrost drzewa, (2) przycinanie drzewa i (3) selekcja drzewa.

Wzrost drzewa

Początkowym etapem tworzenia modelu drzewa decyzyjnego jest wzrost drzewa, który obejmuje dwa kroki: scalanie i podział drzewa. Na początku nieistotne predyktory są kategoryzowane, a istotne kategorie w zbiorze danych grupowane (scalanie drzewa). Wraz ze wzrostem drzewa wzrasta liczba zanieczyszczeń w modelu. Ponieważ obecność zanieczyszczeń może prowadzić do zmniejszenia dokładności modelu, konieczne jest oczyszczenie drzewa. Jednym z możliwych sposobów jest usunięcie zanieczyszczeń na różne liście i rozgałęzienia (podział drzewa) .

Przycinanie drzewa

Przycinanie drzewa, które jest kluczowym elementem drugiego etapu, polega na usunięciu nieistotnych węzłów podziału . Usunięcie nieistotnych węzłów może pomóc zmniejszyć ryzyko utworzenia drzewa nadmiernie dopasowanego. Taka procedura jest szczególnie użyteczna, ponieważ nadmiernie dopasowany model drzewa może prowadzić do błędnej klasyfikacji danych w rzeczywistych zastosowaniach .

Wybór drzewa

Ostatnim etapem opracowywania modelu drzewa decyzyjnego jest wybór drzewa. Na tym etapie utworzony model drzewa decyzyjnego zostanie oceniony za pomocą walidacji krzyżowej lub zestawu danych testowych . Ten etap jest niezbędny, ponieważ może zmniejszyć ryzyko błędnej klasyfikacji danych w rzeczywistych zastosowaniach, a tym samym zminimalizować koszty rozwoju dalszych aplikacji.

Zastosowalność algorytmów drzew decyzyjnych

Przegląd istniejącej literatury pokazuje, że do najczęściej stosowanych algorytmów drzew decyzyjnych należą algorytm Iterative Dichotomiser 3 (ID3), algorytm C4.5, algorytm Chi-squared Automatic Interactive Detector (CHAID) oraz algorytm Classification and Regression Tree (CART). Pomiędzy tymi algorytmami istnieją pewne różnice, z których jedną jest możliwość modelowania różnych typów danych. Ponieważ zbiór danych może być konstruowany z różnych typów danych, np. danych kategorycznych, danych liczbowych lub ich kombinacji, istnieje potrzeba zastosowania odpowiedniego algorytmu drzewa decyzyjnego, który może obsługiwać konkretny typ danych używanych w zbiorze danych. Wszystkie wymienione powyżej algorytmy mogą obsługiwać modelowanie danych kategorycznych, podczas gdy tylko algorytm C4.5 i algorytm CART mogą być używane do modelowania danych liczbowych (patrz Tabela 1). Ta różnica może również służyć jako wskazówka przy wyborze odpowiedniego algorytmu drzewa decyzyjnego. Inną różnicą między tymi algorytmami jest proces rozwoju modelu, zwłaszcza na etapach wzrostu i przycinania drzewa. W odniesieniu do pierwszego, algorytmy ID3 i C4.5 dzielą model drzewa na tyle rozgałęzień, ile jest to konieczne, podczas gdy algorytm CART obsługuje jedynie podziały binarne. W odniesieniu do tego ostatniego, mechanizmy przycinania zawarte w algorytmach C4.5 i CART wspierają usuwanie nieistotnych węzłów i rozgałęzień, natomiast algorytm CHAID utrudnia proces wzrostu drzewa, zanim dane treningowe zostaną nadmiernie wykorzystane.

ZASTOSOWANIA DRZEWA DECYZYJNEGO

Zarządzanie przedsiębiorstwem

W ostatnich dekadach wiele organizacji tworzyło własne bazy danych w celu usprawnienia obsługi klienta. Drzewa decyzyjne to potencjalny sposób na wyodrębnienie użytecznych informacji z baz danych i są już wykorzystywane w wielu zastosowaniach w dziedzinie biznesu i zarządzania. W szczególności modelowanie drzew decyzyjnych jest szeroko stosowane w zarządzaniu relacjami z klientami i wykrywaniu oszustw

Zarządzanie relacjami z klientami

Często stosowanym podejściem do zarządzania relacjami z klientami jest badanie sposobu, w jaki użytkownicy uzyskują dostęp do usług online. Takie badanie przeprowadza się głównie poprzez gromadzenie i analizowanie danych dotyczących korzystania z usług przez użytkowników, a następnie formułowanie rekomendacji na podstawie uzyskanych informacji. Lee i inni stosują drzewa decyzyjne do badania związków między potrzebami i preferencjami klientów a sukcesem zakupów online. W ich badaniu częstotliwość korzystania z zakupów online została wykorzystana jako etykieta do klasyfikowania użytkowników do dwóch kategorii: (a) użytkowników, którzy rzadko korzystają z zakupów online i (b) użytkowników, którzy często korzystają z zakupów online. W odniesieniu do pierwszego z nich, model sugeruje, że czas, jaki klienci muszą poświęcić na transakcję, oraz pilna potrzeba zakupu produktu to najważniejsze czynniki, które należy wziąć pod uwagę. W odniesieniu do drugiego, stworzony model wskazuje, że najważniejszymi czynnikami są cena i stopień zaangażowania zasobów ludzkich (np. wymagania dotyczące kontaktów z pracownikami firmy w celu świadczenia usług). Stworzone drzewa decyzyjne sugerują również, że sukces zakupów online w dużym stopniu zależy od częstotliwości zakupów i ceny produktów. Wnioski uzyskane za pomocą drzew decyzyjnych są przydatne do zrozumienia potrzeb i preferencji klientów.

Wykrywanie fałszywych oświadczeń

Innym powszechnie stosowanym zastosowaniem biznesowym jest wykrywanie fałszywych sprawozdań finansowych (FFS). Takie zastosowanie jest szczególnie ważne, ponieważ istnienie FFS może skutkować zmniejszeniem dochodów podatkowych rządu . Tradycyjnym sposobem identyfikacji FFS jest wykorzystanie metod statystycznych. Jednakże, trudno jest odkryć wszystkie ukryte informacje ze względu na konieczność przyjęcia ogromnej liczby założeń i wstępnego zdefiniowania relacji między dużą liczbą zmiennych w sprawozdaniu finansowym. Wcześniejsze badania dowiodły, że stworzenie drzewa decyzyjnego jest możliwym sposobem rozwiązania tego problemu, ponieważ może ono uwzględniać wszystkie zmienne podczas procesu opracowywania modelu. Kirkos i inni stworzyli model drzewa decyzyjnego w celu identyfikacji i wykrywania FFS. W ich badaniu wybrano 76 greckich firm produkcyjnych, a ich opublikowane sprawozdania finansowe, w tym bilanse i rachunki zysków i strat, zostały zebrane do celów modelowania. Utworzony model drzewa pokazuje, że wszystkie przypadki niezwiązane z oszustwami i 92% przypadków oszustw zostały poprawnie sklasyfikowane. Takie odkrycie wskazuje, że drzewa decyzyjne mogą wnieść znaczący wkład w wykrywanie błędów FFS ze względu na wysoką dokładność.

Inżynieria

Innym ważnym obszarem zastosowań, w którym drzewa decyzyjne mogą być stosowane, jest inżynieria. W szczególności drzewa decyzyjne są szeroko stosowane w diagnostyce zużycia energii i usterek

Zużycie energii
Zużycie energii dotyczy ilości energii elektrycznej zużywanej przez jednostki. Badanie zużycia energii staje się istotną kwestią, ponieważ pomaga firmom użyteczności publicznej określić zapotrzebowanie na energię. Chociaż do badania zużycia energii można wykorzystać wiele istniejących metod, drzewa decyzyjne wydają się być preferowane. Wynika to z faktu, że hierarchiczna struktura zapewniana przez drzewa decyzyjne jest przydatna do prezentacji głębokiego poziomu informacji i wglądu. Na przykład Tso i Yau (2007) stworzyli model drzewa decyzyjnego, aby zidentyfikować zależności między gospodarstwem domowym a jego zużyciem energii elektrycznej w Hongkongu. Wyniki uzyskane dzięki ich modelowi drzewa pokazują, że liczba członków gospodarstwa domowego jest najważniejszym czynnikiem determinującym zużycie energii latem, a zarówno liczba klimatyzatorów, jak i powierzchnia mieszkania są drugimi najważniejszymi czynnikami. Oprócz tych ustaleń, ich model drzewa wskazuje, że gospodarstwo domowe z czterema lub większą liczbą członków, o powierzchni mieszkania większej niż 817 stóp kwadratowych, jest grupą o najwyższym zużyciu energii elektrycznej. Z drugiej strony, gospodarstwa domowe liczące mniej niż czterech członków rodziny i bez klimatyzatorów są grupą o najmniejszym zużyciu energii elektrycznej. Takie ustalenia z drzew decyzyjnych nie tylko zapewniają głębszy wgląd w zużycie energii elektrycznej na danym obszarze, ale także dostarczają firmom energetycznym wskazówek dotyczących właściwego momentu, w którym muszą wygenerować więcej energii elektrycznej.

Diagnostyka usterek

Innym powszechnie stosowanym zastosowaniem w dziedzinie inżynierii jest wykrywanie usterek, zwłaszcza w identyfikacji uszkodzonego łożyska w maszynach obrotowych. Wynika to prawdopodobnie z faktu, że łożysko jest jednym z najważniejszych elementów bezpośrednio wpływających na pracę maszyny obrotowej. Aby wykryć obecność uszkodzonego łożyska, inżynierowie zazwyczaj mierzą sygnały drgań i emisji akustycznej (AE) emitowane przez maszynę obrotową. Pomiar ten obejmuje jednak szereg zmiennych, z których niektóre mogą być mniej istotne dla badania. Drzewa decyzyjne są potencjalnym narzędziem do usuwania takich nieistotnych zmiennych, ponieważ mogą być one wykorzystane do celów selekcji cech. Sugumaran i Ramachandran (2007) stworzyli model drzewa decyzyjnego w celu identyfikacji cech, które mogą znacząco wpłynąć na badanie uszkodzonego łożyska. Poprzez selekcję cech, wybrano trzy atrybuty do rozróżnienia wadliwych warunków łożyska, tj. minimalną wartość sygnału drgań, odchylenie standardowe sygnału drgań oraz kurtozę. Wybrane atrybuty zostały następnie wykorzystane do stworzenia kolejnego modelu drzewa decyzyjnego. Oceny tego modelu pokazują, że ponad 95% testowanego zbioru danych zostało poprawnie sklasyfikowane. Tak wysoki wskaźnik dokładności sugeruje, że usunięcie nieistotnych atrybutów w zbiorze danych jest kolejnym wkładem drzew decyzyjnych.

Zarządzanie opieką zdrowotną

Ponieważ modelowanie drzew decyzyjnych może być wykorzystywane do prognozowania, coraz więcej badań bada możliwość wykorzystania drzew decyzyjnych w zarządzaniu opieką zdrowotną. Na przykład Chang (2007) opracował model drzewa decyzyjnego na podstawie 516 danych, aby zbadać ukrytą wiedzę zawartą w historii medycznej dzieci z opóźnieniem rozwojowym. Stworzony model wskazuje, że większość chorób prowadzi do opóźnień w rozwoju poznawczym, rozwoju mowy i rozwoju motorycznym, których dokładność wynosi odpowiednio 77,3%, 97,8% i 88,6%. Takie ustalenia mogą pomóc pracownikom służby zdrowia we wczesnej interwencji u dzieci z opóźnieniem rozwojowym, aby pomóc im dogonić swoich rówieśników w rozwoju i wzroście. Inny przykład zarządzania opieką zdrowotną można znaleźć w pracy Delen i in. (2005). W ich badaniu stworzono drzewo decyzyjne w celu przewidywania przeżywalności pacjentek z rakiem piersi. Dokładność klasyfikacji w ich drzewie decyzyjnym wynosi 93,6%. Ten wskaźnik klasyfikacji wskazuje, że utworzone drzewo jest bardzo dokładne w przewidywaniu przeżywalności pacjentek z rakiem piersi. Badania te sugerują, że drzewo decyzyjne jest użytecznym narzędziem do odkrywania i eksploracji ukrytych informacji w zarządzaniu opieką zdrowotną.

PRZYSZŁE TRENDY

Wymienione powyżej dziedziny zastosowań pokazują, że drzewo decyzyjne jest bardzo użytecznym narzędziem do analizy danych. Nadal jednak istnieje wiele ograniczeń, których musimy być świadomi i które należy uwzględnić w przyszłych pracach.

Wiarygodność wyników

Chociaż drzewo decyzyjne jest potężnym narzędziem do analizy danych, wydaje się, że niektóre dane są błędnie klasyfikowane w modelach drzew decyzyjnych. Jednym z możliwych sposobów rozwiązania tego problemu jest wykorzystanie wiedzy uzyskanej dzięki współpracy człowieka z komputerem. Innymi słowy, eksperci z różnych dziedzin wykorzystują swoją wiedzę dziedzinową do filtrowania wyników z utworzonego modelu. W ten sposób nieistotne wyniki można ręcznie usunąć. Wadą stosowania takiej metody jest jednak konieczność dużych inwestycji, ponieważ wiąże się ona z kosztami i czasem pracy ekspertów z różnych dziedzin.

Odpowiedniość algorytmów

Jak opisano , opracowanie modelu drzewa decyzyjnego wiąże się z wyborem odpowiedniego algorytmu drzewa decyzyjnego. Oprócz uwzględnienia rodzaju modelowanych danych, konieczne jest rozważenie skuteczności algorytmów. Innym możliwym kierunkiem przyszłych badań jest porównanie skuteczności różnych algorytmów oraz identyfikacja mocnych i słabych stron każdego z nich w różnych typach zastosowań. Ponadto, interesujące byłoby dla przyszłych badań przeprowadzenie porównań między algorytmami drzew decyzyjnych a innymi typami algorytmów klasyfikacyjnych. W ten sposób można by wygenerować wytyczne dotyczące wyboru odpowiednich algorytmów drzew decyzyjnych dla różnych typów zastosowań.

WNIOSKI

Głównym celem niniejszego artykułu jest pomoc czytelnikom w uzyskaniu ogólnego obrazu drzew decyzyjnych poprzez wprowadzenie ich zastosowań w różnych dziedzinach. Aby osiągnąć ten cel, niniejszy artykuł przedstawia przegląd zastosowań modelowania drzew decyzyjnych w zarządzaniu przedsiębiorstwem, inżynierii i zarządzaniu opieką zdrowotną. W każdej dziedzinie zastosowań zidentyfikowano korzyści płynące z tworzenia modelu drzewa decyzyjnego do celów analizy danych i formułowania prognoz. Takie korzyści obejmują: (1) możliwość dokładnego odkrywania ukrytych relacji między zmiennymi, (2) prezentację wiedzy na głębokim poziomie zrozumienia i wglądu w oparciu o jej hierarchiczną strukturę oraz (3) możliwość usuwania nieistotnych atrybutów w zbiorze danych. W niniejszym artykule zbadano trzy dziedziny zastosowań, ale należy zauważyć, że drzewa decyzyjne można również stosować w innych dziedzinach zastosowań, np. bioinformatyce i psychologii. Te dziedziny zastosowań również powinny zostać zbadane. Wyniki takich badań można następnie zintegrować z wynikami niniejszego badania, tak aby można było stworzyć kompletne ramy do wdrażania modeli drzew decyzyjnych. Takie ramy byłyby przydatne do zwiększenia głębokości i szerokości wiedzy na temat modeli drzew decyzyjnych.

WSTĘP

Od czasu wprowadzenia do społeczności badawczej w 1988 r. paradygmat komórkowej sieci neuronowej (CNN) stał się żyzną glebą dla inżynierów i fizyków, którzy w ciągu niecałych 20 lat opublikowali ponad 1000 artykułów naukowych i książek, związane głównie z cyfrowym przetwarzaniem obrazu (DIP). Ta sztuczna sieć neuronowa (ANN) oferuje niezwykłą zdolność integrowania złożonych procesów obliczeniowych w kompaktowe, programowalne w czasie rzeczywistym analogowe obwody VLSI, takie jak ACE16k , a ostatnio w urządzenia FPGA . CNN stanowi rdzeń rewolucyjnego Analogicznego Komputera Komórkowego (Roska i in., 1999), programowalnego systemu opartego na tzw. Uniwersalnej Maszynie CNN (CNN-UM). Analogiczne komputery CNN naśladują anatomię i fizjologię wielu narządów zmysłów i narządów biologicznych przetwarzających.

TŁO

Standardowa architektura CNN składa się z prostokątnego układu M × N komórek C(i,j) o współrzędnych kartezjańskich (i,j), i = 1, 2,…, M, j = 1, 2, … , N. Każdy komórka lub neuron C(i,j) jest ograniczona do sfery wpływów S_r(i,j) o dodatnim promieniu całkowitym r, zdefiniowanym przez:



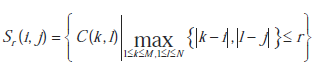
Zbiór ten nazywany jest sąsiedztwem (2r +1) × (2r +1). Parametr r kontroluje łączność komórki. Gdy r > N /2 i M = N, uzyskuje się w pełni połączoną CNN, co odpowiada klasycznemu modelowi SSN Hopfielda. Równanie stanu dowolnej komórki C(i,j) w strukturze tablicowej M × N standardowego CNN można opisać wzorem:



gdzie C i R są wartościami kontrolującymi przejściową odpowiedź obwodu neuronu (podobnie jak filtr RC), I jest ogólnie stałą wartością, która odchyla macierz stanu Z = {z_ij}, a S_r jest lokalnym sąsiedztwem zdefiniowanym w (1 ), który kontroluje wpływ danych wejściowych X = {x_ij} i wyjściowych sieci Y = {y_ij} przez czas t. Oznacza to, że zarówno płaszczyzna wejściowa, jak i wyjściowa oddziałują na stan komórki poprzez definicję zestawu wag o wartościach rzeczywistych A(i, j; k, l) oraz B(i, j; k, l), których rozmiar jest określony przez r. Szablony klonowania A i B nazywane są odpowiednio operatorami sprzężenia zwrotnego i wyprzedzającego. Izotropowy CNN jest zwykle definiowany ze stałymi wartościami r, I, A i B, co oznacza, że dla obrazu wejściowego X dla każdego piksela (i, j) zapewniany jest neuron C(i,j), przy czym zdefiniowane są obwody o stałym obciążeniu poprzez szablony sprzężenia zwrotnego i wyprzedzającego A i B. Wartość stanu neuronu z_ij jest korygowana za pomocą parametru odchylenia I i przekazywana jako dane wejściowe do funkcji wyjściowej w postaci:



Zdecydowana większość szablonów zdefiniowanych w kompendium szablonów CNN-UM opiera się na tym schemacie izotropowym, wykorzystującym r = 1 i obrazy binarne w płaszczyźnie wejściowej. Jeśli nie jest stosowane żadne sprzężenie zwrotne (tj. A = 0), wówczas CNN zachowuje się jak sieć splotów, wykorzystując B jako filtr przestrzenny, I jako próg i fragmentarycznie liniowy sygnał wyjściowy (3) jako ogranicznik. Zatem praktycznie każdy filtr przestrzenny z teorii DIP może zostać zaimplementowany w takim CNN ze sprzężeniem zwrotnym, zapewniając stabilność wyjścia binarnego poprzez definicję wartości bezwzględnej centralnego sprzężenia zwrotnego większej niż 1.

ZAAWANSOWANE PRZETWARZANIE OBRAZU CNN

W tej sekcji dokonano opisu bardziej złożonych modeli CNN, aby zapewnić głębszy wgląd w projekty CNN, w tym struktury wielowarstwowe i szablony nieliniowe, a także zilustrować jego potężne możliwości DIP.

Szablony nieliniowe

Problemem często poruszanym przy wykrywaniu krawędzi DIP jest odporność na szum . W tym sensie detektor EDGE CNN do obrazów w skali szarości nadawanych przez



jest typowym przykładem filtra słabego przeciwzakłóceniowego, powstałego w wyniku ustalonego liniowego szablonu wyprzedzającego w połączeniu z pobudzającym sprzężeniem zwrotnym. Jednym ze sposobów zapewnienia większej odporności detektora na szum jest zdefiniowanie nieliniowego szablonu B w postaci:



Ten nieliniowy szablon w rzeczywistości definiuje różne współczynniki dla otaczających pikseli przed wykonaniem przestrzennego filtrowania obrazu wejściowego X. Zatem CNN zdefiniowana za pomocą nieliniowych szablonów jest ogólnie zależna od X i nie można jej traktować jako modelu izotropowego. Dopuszczalne są tylko dwie wartości otaczających współczynników B: jedna pobudzająca dla różnic w luminancji większych niż próg th w stosunku do piksela centralnego (tj. pikseli brzegowych), a druga hamująca, podwojona w wartości bezwzględnej, dla podobnych pikseli, gdzie th zwykle wynosi ustawić na około 0,5. Szablon sprzężenia zwrotnego A = 2 pozostaje niezmieniony, ale wartość obciążenia I należy wybrać z następującej analizy: Dla danego elementu z_ij stanu udział w_ij nieliniowego filtra wyprzedzającego (5) można wyrazić jako:



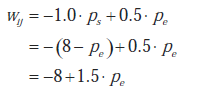
gdzie p_s to liczba podobnych pikseli w sąsiedztwie 3 × 3, a p_e pozostałych pikseli krawędziowych. Np. jeśli centralny piksel ma 8 sąsiadów krawędziowych, w_ij = 12 - 8 = 4, natomiast jeśli wszyscy jego sąsiedzi są do niego podobni, to w_ij = -8. Zatem piksel zostanie wybrany jako krawędź w zależności od liczby jego sąsiadów na krawędzi, zapewniając możliwość redukcji szumu. Na przykład wykrywanie krawędzi dla pikseli z co najmniej 3 sąsiadami krawędziowymi wymusza I ∈ (4, 5). Głównym rezultatem jest to, że włączenie nieliniowości do definicji współczynników B, a co za tym idzie, definicja głównych parametrów CNN w ujęciu pikselowym powoduje powstanie potężniejszych i bardziej złożonych filtrów DIP

Operatory morfologiczne

Morfologia matematyczna wnosi ważny wkład w dziedzinę DIP. W podejściu klasycznym każdy operator morfologiczny opiera się na szeregu prostych koncepcji z Teorii Mnogości. Ponadto wszystkie można podzielić na kombinacje dwóch podstawowych operatorów: erozji i dylatacji. Obydwa operatory przyjmują jako dane wejściowe dwie części danych: binarny obraz wejściowy i tzw. element strukturujący, który jest zwykle reprezentowany przez szablon 3×3. Piksel należy do obiektu, jeśli jest aktywny (tj. jego wartość wynosi 1 lub jest czarny), natomiast pozostałe piksele są klasyfikowane jako elementy tła o wartości zerowej. Podstawowe operatory morfologiczne definiowane są przy użyciu wyłącznie pikseli obiektu, oznaczonych jako 1 w elemencie strukturalnym. Jeśli piksel nie jest używany w dopasowaniu, pozostaje pusty. Zarówno operatory dylatacji, jak i erozji można zdefiniować za pomocą elementów strukturalnych.



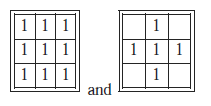
odpowiednio dla łączności 8 lub 4 sąsiadów. W przypadku dylatacji element nadający strukturę jest umieszczany nad każdym pikselem wejściowym. Jeśli którykolwiek z 9 (lub 5) pikseli rozważanych w (7) jest aktywny, wówczas aktywny będzie również piksel wyjściowy . Operator erozji można zdefiniować jako dualność dylatacji, czyli dylatacji wykonywanej na tle. Bardziej złożone operatory morfologiczne opierają się na elementach strukturalnych, które zawierają również piksele tła. Tak jest w przypadku transformacji Hit and Miss Transform (HMT), uogólnionego operatora morfologicznego używanego do identyfikacji pewnych lokalnych konfiguracji pikseli. Na przykład elementy strukturalne zdefiniowane przez



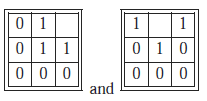
służą do wyszukiwania wypukłych pikseli obiektu narożnego pod kątem 90° na obrazie. Piksel zostanie wybrany jako aktywny w obrazie wyjściowym, jeśli jego lokalne sąsiedztwo dokładnie odpowiada temu określonemu przez element nadający strukturę. Jednakże, aby obliczyć pełny, niezorientowany detektor narożny, konieczne będzie wykonanie 8 HMT, po jednym dla każdej obróconej wersji (8), OR-ing 8 pośrednich obrazów wyjściowych w celu uzyskania obrazu końcowego. W kontekście CNN HMT można uzyskać w prosty sposób poprzez:



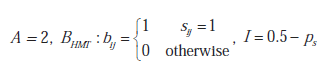
(9) gdzie S = {s_ij} jest elementem strukturalnym, a p_s jest całkowitą liczbą aktywnych pikseli. Ponieważ szablon wejściowy B HTM CNN jest zdefiniowany poprzez element strukturalny S i biorąc pod uwagę, że istnieje 2₉ = 512 różnych możliwych elementów strukturalnych 3 × 3, będzie również 512 różnych erozji typu hit-and-mis. Aby osiągnąć odwrotny wynik, tj. Rozszerzenie typu hit-and-miss, próg musi być przeciwny do tego w (9)

Kontrola zakresu dynamicznego CNN i fragmentaryczne mapowania liniowe

Techniki DIP można klasyfikować według dziedziny, w której operują: domena obrazowa lub przestrzenna lub domena transformacji (np. domena Fouriera). Techniki domeny przestrzennej to te, które działają bezpośrednio na pikselach obrazu (np. Na jego poziomie intensywności). Ogólny operator przestrzenny można zdefiniować za pomocą



gdzie X i Y są odpowiednio obrazami wejściowymi i wyjściowymi, a T jest operatorem przestrzennym zdefiniowanym w sąsiedztwie Sr wokół każdego piksela X(i, j), jak zdefiniowano w (1). W oparciu o to sąsiedztwo operatory przestrzenne można podzielić na dwa typy: operatory przetwarzania jednopunktowego, znane również jako operatory mapowania, oraz operatory przetwarzania lokalnego, które można zdefiniować za pomocą maski filtra przestrzennego (tj. splotu dyskretnego 2D) (Jain, 1989). ). Najprostszą postać T uzyskuje się, gdy Sr ma rozmiar 1 piksela. W tym przypadku Y zależy tylko od wartości intensywności X dla każdego piksela, a T staje się funkcją transformacji poziomu intensywności, czyli mapowaniem, w postaci

s = T(r) gdzie X i Y są odpowiednio obrazami wejściowymi i wyjściowymi, a T jest operatorem przestrzennym zdefiniowanym w sąsiedztwie Sr wokół każdego piksela X(i, j), jak zdefiniowano w (1). W oparciu o to sąsiedztwo operatora przestrzennego można podzielić na dwa typy: operatory przetwarzania jednopunktowego, znane również jako operatory mapowania, oraz operatory przetwarzania lokalnego, które można zdefiniować za pomocą maski filtra przestrzennego (tj. splotu dyskretnego 2D) . Najprostszą postać T uzyskuje się, gdy Sr ma rozmiar 1 piksela. W tym przypadku Y zależy tylko od wartości intensywności X dla każdego piksela, a T staje się funkcją transformacji poziomu intensywności lub mapowaniem w postaci +1] zakresu. Odchylenie I kontroluje średni punkt zakresu wejściowego, gdzie funkcja wyjściowa daje wynik o wartości zerowej. Zaczynając od oryginalnej komórki lub neuronu CNN (1)-(3), następuje krótki przegląd modelu CNN kontroli zakresu dynamicznego (DRC), zdefiniowanego po raz pierwszy w . Sieć ta jest zaprojektowana do wykonywania fragmentarycznego liniowego odwzorowania T na X, z zakresem wejściowym [m-d, m+d] i zakresem wyjściowym [a, b]. Zatem,



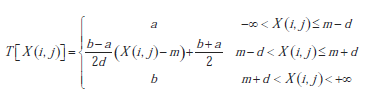
(12) Aby móc realizować tę funkcję w wielowarstwowym CNN, muszą zostać spełnione następujące ograniczenia:

|b-a| ≤ i d ≤ 1 (13) Komórkę CNN kontrolującą żądany zakres wejściowy można zdefiniować za pomocą następujących parametrów:

A₁ = 0 , B₁ = 1/d I₁ = -m/d

(14) Sieć ta wykonuje mapowanie liniowe pomiędzy [m-d, m+d] i [-1,+1]. Jego wyjście jest wejściem drugiego CNN, którego parametry to:

A₂, B₂ = (b -a)/2 , I₂ = (b + a)/2

(15) Wynikiem tej drugiej sieci jest dokładnie odwzorowanie T zdefiniowane w (12) ograniczone ograniczeniami (13). Jedną z najprostszych technik stosowanych w celu zwiększenia kontrastu obrazu w skali szarości jest rozciąganie kontrastu lub normalizacja. Technika ta maksymalizuje zakres dynamiczny poziomów intensywności na obrazie na podstawie odpowiednich szacunków maksymalnych i minimalnych wartości intensywności. Zatem w przypadku znormalizowanych obrazów w skali szarości, gdzie minimalny (tj. czarny) i maksymalny (tj. biały) poziom intensywności są reprezentowane odpowiednio przez wartości 0 i 1; jeśli taki obraz o zakresie intensywności dynamicznej [f, g] ⊆ [0, +1] zostanie podany na wejście 2-warstwowego CNN określonego przez (14) i (15), to następujące parametry pozwolą uzyskać pożądaną dynamikę liniową maksymalizacja zasięgu:

a = 0 , b = 1 , m = (g +f)/2 , d = (g-f)/2

Sieć DRC można łatwo zastosować do odcinkowego przybliżenia wielomianowego pierwszego rzędu nieliniowych, ciągłych odwzorowań. Jedną z możliwych możliwości jest wielowarstwowa implementacja wielomianów Czebyszewa sterowanych błędami w DRC CNN, jak opisano. Możliwe odwzorowania obejmują między innymi funkcje wartości bezwzględnej, logarytmicznej, wykładniczej, radialnej oraz funkcje potęgowe o wartościach całkowitych i rzeczywistych.

PRZYSZŁE TRENDY

Inżynierowie i specjaliści nieustannie poszukują: konkurować i naśladować naturę, zwłaszcza niektóre "inteligentne" zwierzęta. Wizja to szczególny obszar zainteresowania inżynierów komputerów. W tym kontekście tak zwane oko bioniczne osadzone w architekturze CNN-UM idealnie nadaje się do realizacji wielu czasoprzestrzennych modeli neuromorficznych. Dzięki potężnemu zestawowi narzędzi do przetwarzania obrazu i kompaktowej implementacji VLSI CNN-UM może być używany do programowania lub naśladowania różnych modeli siatkówek, a nawet ich kombinacji. Co więcej, może łączyć modele oparte na biologii, modele inspirowane biologią i modele analogiczne algorytmy przetwarzania sztucznego obrazu. To połączenie z pewnością przyniesie szerszy rodzaj zastosowań i rozwiązań.

WNIOSEK

W ostatniej dekadzie zbadano szereg innych postępów w definicji i charakterystyce CNN. Obejmuje to definicję metod projektowania i wdrażania dzielnic o wymiarach większych niż 3×3 w CNN-UM , wdrażanie przez CNN niektórych technik kompresji obrazu lub projektowanie Algorytm szybkiej transformacji Fouriera oparty na CNN dla sygnałów analogowych oraz wiele innych. W tym artykule dokonano ogólnego przeglądu głównych właściwości i cech modelu komórkowej sieci neuronowej, koncentrując się na jej zastosowaniach DIP. CNN jest obecnie podstawowym i potężnym zestawem narzędzi do zadań nieliniowego przetwarzania obrazu w czasie rzeczywistym, głównie ze względu na jego wszechstronną programowalność, która umożliwiła rozwój sprzętu do zastosowań w czujnikach wizualnych

WSTĘP

Mechanizmy sztucznej inteligencji (AI) są coraz częściej stosowane do wszelkiego rodzaju problemów inżynierii lądowej. Nowe metody i algorytmy, które pozwalają inżynierom lądowym na wykorzystywanie tych technik w różny sposób w przypadku różnych problemów, są dostępne lub są udostępniane. Jedna z technik AI wyróżnia się na tle pozostałych: sztuczne sieci neuronowe (ANN). Ich najbardziej niezwykłymi cechami są zdolność uczenia się, możliwość generalizacji i tolerancja na błędy. Te cechy sprawiają, że ich stosowanie jest opłacalne i opłacalne w każdej dziedzinie, a w szczególności w inżynierii budowlanej. Obecnie najbardziej rozpowszechnionym materiałem budowlanym jest beton, głównie ze względu na jego wysoką wytrzymałość i możliwość dostosowania do szalunków podczas procesu produkcji. W tym rozdziale znajdziemy różne zastosowania ANN do betonu konstrukcyjnego.

Sztuczne sieci neuronowe

Warren McCulloch i Walter Pitts są uznawani za twórców sztucznych sieci w latach 40. XX wieku, ponieważ jako pierwsi zaprojektowali sztuczny neuron . Zaproponowali model neuronu w trybie binarnym (aktywnym lub nieaktywnym) ze stałym progiem, który musi zostać przekroczony, aby zmienić stan. Niektóre z wprowadzonych przez nich koncepcji są nadal przydatne. Sztuczne sieci neuronowe mają na celu symulację właściwości występujących w biologicznych systemach neuronowych za pomocą modeli matematycznych za pomocą sztucznych mechanizmów. Neuron jest uważany za formalny element, moduł lub podstawową jednostkę sieciową, która odbiera informacje z innych modułów lub środowiska; następnie integruje i oblicza te informacje, aby wyemitować pojedyncze wyjście, które zostanie identycznie przesłane do kolejnych wielu neuronów (Wasserman, 1989). Wyjście sztucznego neuronu jest określane przez jego funkcje propagacji lub wzbudzenia, aktywacji i transferu. Funkcja propagacji jest na ogół sumą każdego wejścia pomnożonego przez wagę jego połączenia (wartość netto):



Funkcja aktywacji modyfikuje ten ostatni, wiążąc sygnał wejściowy neuronalny z kolejnym stanem aktywacji.



Funkcja przejścia jest stosowana do wyniku funkcji aktywacji. Służy do ograniczenia wyjścia neuronu i jest zazwyczaj podawana przez interpretację przeznaczoną dla wyjścia. Niektóre z najczęściej używanych funkcji przejścia to sigmoidalna (aby uzyskać wartości w przedziale [0,1]) i hiperboliczna tangensowa (aby uzyskać wartości w przedziale [-1,1]).

out_i = FT(a_i(t) Po zdefiniowaniu każdego elementu procesu należy zaprojektować typ sieci (topologię sieci), która ma zostać użyta. Można je podzielić na sieci forward-feed, w których informacje przemieszczają się tylko w jednym kierunku (od wejścia do wyjścia) oraz sieci z częściowym lub całkowitym sprzężeniem zwrotnym, w których informacje mogą płynąć w dowolnym kierunku. Na koniec należy zdefiniować reguły uczenia się i typ szkolenia. Reguły uczenia się dzielą się na nadzorowane i nienadzorowane , a w ramach tych ostatnich, samoorganizujące się uczenie się i uczenie się przez wzmacnianie . Typ szkolenia będzie zależał od wybranego typu uczenia się.

Wprowadzenie do betonu (materiał i struktura)

Beton konstrukcyjny to materiał budowlany wytwarzany z mieszanki cementu, wody, kruszyw i dodatków lub domieszek o różnych funkcjach. Celem jest stworzenie materiału o wyglądzie skały, o wystarczającej wytrzymałości na ściskanie i zdolności do przyjmowania odpowiednich kształtów strukturalnych. Beton jest formowalny w fazie przygotowywania, po wymieszaniu składników powstaje płynna masa, która wygodnie zajmuje wnęki w formie zwanej szalunkiem. Po kilku godzinach beton twardnieje dzięki reakcji chemicznej hydratacji eksperymentowanej z cementem, generując pastę, która otacza kruszywa i nadaje zespołowi wygląd sztucznej skały nieco podobnej do konglomeratu. Stwardniały beton oferuje dobrą wytrzymałość na ściskanie, ale bardzo niską wytrzymałość na rozciąganie. Dlatego konstrukcje wykonane z tego materiału muszą być wzmacniane za pomocą stalowych prętów zbrojeniowych, skonfigurowanych za pomocą prętów, które są umieszczane (przed wylaniem betonu) wzdłuż linii, gdzie obliczenia przewidują najwyższe naprężenia rozciągające. Pękanie, które zmniejsza trwałość konstrukcji, jest w ten sposób utrudnione, a wystarczająca wytrzymałość jest gwarantowana przy bardzo niskim prawdopodobieństwie awarii. Całość utworzona z betonu i prętów zbrojeniowych jest określana jako beton konstrukcyjny. Dwie fazy charakteryzują zatem ewolucję betonu w czasie. W pierwszej fazie beton musi być wystarczająco płynny, aby zapewnić łatwość układania, a czas początkowego wiązania musi być wystarczająco długi, aby umożliwić transport z zakładu na miejsce pracy. Płynność zależy zasadniczo od rodzaju i ilości składników w mieszance. Specjalne domieszki chemiczne (takie jak plastyfikatory i superplastyfikatory) gwarantują płynność bez znacznego zwiększania ilości wody, której stosunek w stosunku do ilości cementu (lub stosunek woda/cement, w/c) jest odwrotnie proporcjonalny do uzyskanej wytrzymałości. Nauka reologii zajmuje się badaniem zachowania świeżego betonu. Do określenia płynności świeżego betonu można zastosować różne testy, z których najpopularniejszym jest test stożka Abramsa lub test stożka opadowego . Druga faza (i najdłuższa w czasie) to faza stwardniałego betonu, która określa zachowanie struktury, której nadaje kształt, z punktu widzenia użyteczności (poprzez narzucenie ograniczeń na pękanie i podatność) i odporności na awarie (poprzez narzucenie ograniczeń na minimalne obciążenia, którym można się oprzeć, w porównaniu z siłami wewnętrznymi wytwarzanymi przez obciążenie zewnętrzne), zawsze w ramach wystarczającej trwałości dla przewidywanego okresu użytkowania. Badanie betonu konstrukcyjnego z każdego punktu widzenia zostało podjęte zgodnie z wieloma różnymi optykami. Ścieżka eksperymentalna była bardzo produktywna, generując w ciągu ostatnich 50 lat bazę danych (z tendencją do rozproszenia), która została wykorzystana do zatwierdzenia badań prowadzonych wzdłuż drugiej i trzeciej ścieżki, które następują. Ścieżka analityczna stanowi również podstawowe narzędzie do podejścia do zachowania betonu, zarówno z punktu widzenia materiału, jak i konstrukcji. Rozwój teoretycznych modeli zachowań sięga początku XX wieku, a opracowane od tego czasu równania teoretyczne były korygowane poprzez testowanie (jak wspomniano powyżej), zanim stały się częścią kodów i specyfikacji. Ta metoda analizy została wzmocniona przez rozwój metod numerycznych i systemów obliczeniowych, zdolnych do rozwiązywania dużej liczby równoczesnych równań. W szczególności metoda elementów skończonych (i inne metody z tej samej rodziny) oraz techniki optymalizacji przyniosły niezwykłą zdolność do przybliżania zachowania betonu konstrukcyjnego, a ich wyniki zostały porównane w wielu zastosowaniach za pomocą wyżej wymienionych testów eksperymentalnych. Dostępne są zatem trzy podstawowe kierunki badań. Będąc wzajemnie uzupełniającymi się, odegrały decydującą rolę w produkcji krajowych i międzynarodowych kodów i zasad, które kierują lub stanowią prawodawstwo w zakresie projektu, wykonania i konserwacji prac z betonu konstrukcyjnego. Beton jest złożonym materiałem, który stwarza szereg problemów dla badań analitycznych, a zatem jest odpowiednim polem do rozwoju technik analizy opartych na sieciach neuronowych. Zastosowanie sztucznych sieci neuronowych do problemów w dziedzinie betonu konstrukcyjnego rozwinęło się w ciągu ostatnich kilku lat na dwa sposoby. Z jednej strony, analityczne i konstrukcyjne systemy optymalizacji szybsze niż tradycyjne (zwykle iteracyjne) metody zostały wygenerowane zaczynając od wyrażeń i reguł obliczeniowych. Z drugiej strony, liczne bazy danych utworzone z dużej liczby testów opublikowanych w społeczności naukowej pozwoliły na rozwój bardzo wydajnych ANN, które rzuciły światło na różne złożone zjawiska. W kilku przypadkach, konkretne zaprojektowane kody zostały ulepszone poprzez wykorzystanie tych technik; poniżej przedstawiono kilka przykładów.

Zastosowanie sztucznych sieci neuronowych w problemach optymalizacji

Projektowanie konstrukcji betonowych opiera się na określeniu dwóch podstawowych parametrów: grubości elementu (efektywnej głębokości d, głębokości przekroju belki lub płyty mierzonej od powierzchni ściskanej do środka ciężkości zbrojenia) i ilości zbrojenia (ustalonej jako całkowita powierzchnia As stali w przekroju, zmaterializowanej jako pręty zbrojeniowe lub współczynnik zbrojenia, stosunek powierzchni stali do powierzchni betonu w przekroju). Metody obliczeniowe są iteracyjne, ponieważ w konstrukcji należy zweryfikować dużą liczbę warunków, a wyżej wymienione parametry są ustalone jako funkcja trzech podstawowych warunków, które są kolejno przestrzegane: bezpieczeństwo konstrukcyjne, maksymalna ciągliwość przy zniszczeniu i minimalny koszt. Reguły projektowania, wyrażone za pomocą równań, pozwalają na pierwsze rozwiązanie, które jest korygowane tak, aby spełniało wszystkie scenariusze obliczeniowe, ostatecznie zbieżne, gdy różnica między parametrami wejściowymi i wyjściowymi jest nieistotna. W niektórych przypadkach możliwe jest opracowanie algorytmów optymalizacyjnych, których analityczne sformułowanie otwiera drogę do wygenerowania bazy danych. Hadi wykonał tę pracę dla belek żelbetowych podpartych w prosty sposób, a wyrażenia uzyskane po procesie optymalizacji określają parametry określone powyżej, przy jednoczesnym przypisaniu kosztu związanego z optymalnym rozwiązaniem (związanego z kosztem materiałów i deskowania). Za pomocą tych wyrażeń Hadi opracowuje bazę danych z następującymi zmiennymi: zastosowany moment zginający (M), wytrzymałość betonu na ściskanie (fc), wytrzymałość stali (fy), szerokość przekroju (b), głębokość przekroju (h) oraz koszty jednostkowe betonu (Cc), stali (Cs) i deskowania (Cf). Użyte parametry sieci są następujące. Liczba próbek treningowych wynosi 550; liczba neuronów warstwy wejściowej wynosi 8; liczba neuronów warstwy ukrytej wynosi 10; liczba neuronów warstwy wyjściowej wynosi 4; typ propagacji wstecznej to propagacja wsteczna Levenberga-Marquardta; funkcja aktywacji jest funkcją sigmoidalną; szybkość uczenia się; 0,01; liczba epok wynosi 3000; suma kwadratów błędu wynosi 0,08. Sieć została przetestowana na 50 próbkach i dała średni błąd 6,1%. Hadi bada różne czynniki przy wyborze architektury sieci i typu algorytmu propagacji wstecznej. Gdy używane są dwie warstwy ukrytych neuronów, precyzja nie ulega poprawie, podczas gdy czas obliczeń wzrasta. Liczba próbek zależy od złożoności problemu i liczby parametrów wejściowych i wyjściowych. Jeśli wartość kosztów wejściowych jest stała, nie ma zauważalnych ulepszeń precyzji między trenowaniem sieci z 200 lub 1000 próbek. Gdy koszty są wprowadzane jako parametry wejściowe, 100 próbek nie wystarcza do osiągnięcia zbieżności w treningu. Na koniec sprawdzany jest również algorytm treningowy, badając zakres między czystą propagacją wsteczną (zbyt wolną do treningu), propagacją wsteczną z pędem i adaptacyjnym uczeniem się, propagacją wsteczną z regułą aktualizacji Levenberga-Marquardta i szybką propagacją wsteczną uczenia się. Ta ostatnia jest ostatecznie zachowana, ponieważ wymaga mniej czasu, aby sieć zbiegła się, zapewniając jednocześnie bardzo dobre wyniki

Zastosowanie sztucznych sieci neuronowych do przewidywania mierzalnych parametrów fizycznych betonu: wytrzymałości i konsystencji betonu

Inne zastosowania sieci neuronowych są wspierane przez duże bazy danych eksperymentalnych, tworzone przez lata badań, które pozwalają na przewidywanie zjawisk o złożonej formulacji analitycznej. Jednym z takich przypadków jest określenie dwóch podstawowych parametrów betonu: jego urabialności po wymieszaniu, niezbędnej do łatwego umieszczania w betonie, oraz jego wytrzymałości na ściskanie po stwardnieniu, która jest podstawą oceny nośności konstrukcji. Zmiennymi, które koniecznie określają te dwa parametry, są składniki betonu: ilości cementu, wody, drobnego kruszywa (piasku), grubego kruszywa (drobnego żwiru i dużego żwiru) oraz inne składniki, takie jak dodatki pucolanowe (które zapewniają solidność i opóźniony wzrost wytrzymałości, szczególnie w przypadku popiołu lotnego i pyłu krzemionkowego) i domieszki (które upłynniają świeżą mieszankę, umożliwiając użycie zmniejszonych ilości wody). Nadal nie ma modeli analitycznych ani numerycznych, które wiernie przewidują konsystencję świeżego betonu (związaną z płynnością i zwykle ocenianą na podstawie opadu uformowanego stożka betonowego) lub wytrzymałość na ściskanie (określoną przez kruszenie pryzmatycznych próbek w prasie). Öztaş i inni opracowali sieć neuronową na podstawie 187 mieszanek betonowych, dla których znane są wszystkie parametry, wykorzystując 169 z nich do treningu i 18 wybranych losowo do weryfikacji. Zmienne bazy danych są czasami traktowane jako stosunek między nimi, ponieważ dostępna jest wiedza na temat zależności opadu i wytrzymałości od takich parametrów.Architektura sieci, określona przez 7 neuronów wejściowych i dwie ukryte warstwy odpowiednio 5 i 3 neuronów. Algorytm uczenia się wstecznej propagacji został użyty w dwóch ukrytych warstwach z sprzężeniem do przodu. Algorytm uczenia się użyty w badaniu to algorytm skalowanych gradientów sprzężonych (SCGA), funkcja aktywacji jest funkcją sigmoidalną, a liczba epok wynosi 10 000. Zdolność predykcyjna sieci jest lepsza w przypadku wyjścia "Wytrzymałość na ściskanie" (maksymalny błąd 6%) niż w przypadku wyjścia "Opad" (błędy do 25%). Wynika to z faktu, że związek między wybranymi zmiennymi a wytrzymałością jest znacznie silniejszy niż w przypadku opadu, na który wpływają inne nieuwzględniane zmienne (np. rodzaj i moc betoniarki, kolejność mieszania składników, wilgotność kruszywa) oraz metoda pomiaru konsystencji, której adekwatność dla konkretnego rodzaju betonu użytego w bazie danych jest kwestionowana przez niektórych autorów.

Zastosowanie sztucznych sieci neuronowych do opracowywania wzorów i kodów projektowych

Ostatnim zastosowaniem przedstawionym w tym artykule jest analiza odpowiedzi na siły ścinające w belkach betonowych. Siły te generują poprzeczne naprężenia rozciągające w belkach betonowych, które wymagają umieszczenia prętów zbrojeniowych prostopadle do osi belki, znanych jako obręcze lub wiązania. Analityczne określenie obciążenia niszczącego ze zmiennych, które wpływają na ten problem, jest bardzo złożone i ogólnie rzecz biorąc większość wzorów stosowanych obecnie opiera się na eksperymentalnych interpolacjach bez spójności wymiarowej. Cladera i Marí zbadali ten problem poprzez testy laboratoryjne, opracowując sieć neuronową do analizy wytrzymałości belek bez zbrojenia ścinającego. Opierają się na bazie danych skompilowanej przez Bentza i Kuchmę, gdzie zmiennymi są efektywna głębokość (d), szerokość belki (b, choć wprowadzono ją jako d/b), rozpiętość ścinania, współczynnik zbrojenia podłużnego (?l = As/bd) i wytrzymałość betonu na ściskanie (fc). Oczywiście obciążenie niszczące jest podawane dla każdego z 177 testów znalezionych w bazie danych. Używają 147 testów do trenowania sieci i 30 do weryfikacji, na architekturze jednowarstwowej z 10 ukrytymi neuronami i mechanizmem uczenia się retropropagacji. Aby uzyskać najlepsze wyniki, potrzebnych było prawie 8000 iteracji. Dostosowanie dostarczone przez trening przedstawia średni współczynnik Vtest/Vpred wynoszący 0,99 i 1,02 w walidacji. Autorzy skutecznie stworzyli laboratorium z siecią neuronową, w którym "testują" (w zakresie parametrów) nowe belki, zmieniając wyłącznie jeden parametr za każdym razem. Na koniec wymyślają dwa alternatywne wzory projektowe, które zauważalnie poprawiają każdy dany wzór opracowany do tego momentu. Tabela 3 przedstawia porównanie tych dwóch wyrażeń (nazwanych równaniem 7 i równaniem 8) z innymi znalezionymi w serii międzynarodowych kodów.Ö

WNIOSEK

•  Dziedzina betonu konstrukcyjnego wykazuje duży potencjał do zastosowania sieci neuronowych. Przedstawiono udane podejścia do optymalizacji, przewidywania złożonych parametrów fizycznych i opracowywania wzorów projektowych. Topologia sieci stosowana w większości przypadków dla betonu konstrukcyjnego jest typu forward-feed, wielowarstwowa z propagacją wsteczną, zazwyczaj z jedną lub dwiema ukrytymi warstwami. Najczęściej stosowanymi algorytmami szkoleniowymi są gradient zstępujący z pędem i adaptacyjne uczenie się oraz Levenberg-Marquardt.
•  Największym potencjałem sieci neuronowych jest ich zdolność do generowania wirtualnych laboratoriów testowych, które zastępują precyzyjne drogie rzeczywiste testy laboratoryjne w odpowiednim zakresie wartości. Metodyczny program "testowania" rzuca światło na wpływ różnych zmiennych w złożonych zjawiskach przy obniżonych kosztach.
•  Dziedzina betonu konstrukcyjnego opiera się na rozległych bazach danych, generowanych przez lata, które można analizować za pomocą tej techniki. Należy podjąć wysiłki w celu skompilowania i ujednolicenia tych baz danych w celu wyodrębnienia maksymalnej możliwej wiedzy, która ma duży wpływ na bezpieczeństwo konstrukcyjne.

WSTĘP

Klasyczne szyfry służą do szyfrowania wiadomości tekstowych napisanych w języku naturalnym w taki sposób, że są one czytelne tylko dla nadawcy lub zamierzonego odbiorcy. Wiele klasycznych szyfrów można złamać metodą siłowego przeszukiwania przestrzeni klucza. Jednym z istotnych problemów pojawiających się w zautomatyzowanej kryptoanalizie jest rozpoznawanie tekstu jawnego. Komputer powinien być w stanie zdecydować, które z wielu możliwych odszyfrowania są sensowne. Można to osiągnąć za pomocą funkcji punktacji tekstu, opartej np. na n-gramach lub innych statystykach tekstu. Funkcja punktacji może być również używana w połączeniu z metodami AI w celu przyspieszenia kryptoanalizy.

TŁO

Rozpoznawanie języka to dziedzina sztucznej inteligencji badająca, jak wykorzystywać komputery do rozpoznawania języka tekstu. Jest to proste zadanie, gdy mamy wystarczającą ilość tekstu z akcentami, ponieważ charakteryzują one używany język z bardzo dużą dokładnością. Obecnie istnieje wiele zestawów narzędzi, które automatycznie sprawdzają/korygują często zarówno błędy ortograficzne, jak i gramatyczne. W związku z tym przypominamy również ocenę rozpoznawania języka NIST (LRE-05, LRE-07) jako część trwającej serii ocen technologii rozpoznawania języka. McMahon i Smith (1998) przedstawiają przegląd technik przetwarzania języka naturalnego opartych na modelach statystycznych. Przypominamy kilka podstawowych pojęć z kryptografii (więcej szczegółów można znaleźć w artykule zautomatyzowana kryptoanaliza klasycznych szyfrów). Istnieje odwracalna reguła szyfrowania (algorytm), jak przekształcić tekst jawny w tekst zaszyfrowany i odwrotnie. Algorytmy te zależą od tajnego parametru K zwanego kluczem. Zestaw możliwych kluczy K nazywany jest przestrzenią kluczy. Wejściem i wyjściem tych algorytmów jest ciąg liter z tekstu jawnego lub alfabetu tekstu zaszyfrowanego. Zarówno nadawca, jak i odbiorca używają tego samego tajnego klucza i tych samych algorytmów szyfrowania i deszyfrowania. Kryptoanaliza to proces odzyskiwania klucza lub odzyskiwania tekstu jawnego bez znajomości klucza. W obu przypadkach potrzebujemy podprogramu rozpoznawania tekstu jawnego, który ocenia (z pewnym prawdopodobieństwem) każdy kandydujący podciąg, czy jest to poprawny tekst jawny, czy nie. Takie automatyczne rozpoznawanie tekstu wymaga odpowiedniego modelu używanego języka.

ROZPOZNAWANIE TEKSTU JAWNEGO DLA AUTOMATYCZNEJ KRYPTANALIZY

W procesie automatycznej kryptoanalizy odszyfrowujemy tekst zaszyfrowany wieloma możliwymi kluczami, aby uzyskać kandydujące teksty jawne. Większość kandydatów jest niepoprawna, nie mająca znaczenia w języku naturalnym. Z drugiej strony, nawet poprawny tekst jawny może być trudny do rozpoznania, a przy złej procedurze rozpoznawania może zostać całkowicie pominięty. Podstawowym typem algorytmu odpowiednim do automatycznej kryptoanalizy jest atak siłowy. Ten atak jest wykonalny tylko wtedy, gdy przestrzeń kluczy jest przeszukiwalna w zasobach obliczeniowych dostępnych dla atakującego. Średni czas potrzebny do zweryfikowania kandydata silnie wpływa na rozmiar przeszukiwanej przestrzeni kluczy. Zatem rozpoznawanie tekstu jawnego jest najważniejszą częścią algorytmu z punktu widzenia wydajności. Z drugiej strony, tylko najbardziej złożone algorytmy osiągają naprawdę wysoką dokładność rozpoznawania tekstu jawnego. Zatem złożoność i dokładność algorytmów rozpoznawania tekstu jawnego muszą być starannie zrównoważone. Algorytm integruje trzy warstwy rozpoznawania tekstu jawnego, a mianowicie predykat testu negatywnego, szybką funkcję punktacji i precyzyjną funkcję punktacji, jako filtr trójwarstwowy. Ostateczna funkcja punktacji jest również używana do sortowania wyników. Pierwszy filtr powinien być bardzo szybki, z bardzo niskim prawdopodobieństwem błędu. Szybki wynik powinien być łatwy do obliczenia, ale nie jest wymagany do precyzyjnej identyfikacji poprawnego tekstu jawnego. Poprawne rozpoznawanie tekstu jawnego jest rolą precyzyjnej funkcji punktacji. W algorytmie najlepszy wynik jest najwyższy. Jeśli wynik jest obliczany w przeciwnym znaczeniu, algorytm musi zostać odpowiednio przepisany. W niektórych przypadkach możemy zintegrować szybką funkcję punktacji w teście negatywnym lub z precyzyjną punktacją, co prowadzi do filtrów dwuwarstwowych. Możliwe jest również użycie jeszcze większej liczby kroków filtrowania opartego na predykatach i wynikach. Jednak eksperymenty pokazują, że proponowana architektura trzech warstw jest najbardziej elastyczna, a więcej warstw może nawet prowadzić do spadku wydajności.

Filtrowanie negatywne

Celem predykatu testu negatywnego jest identyfikacja tekstów kandydackich, które NIE są tekstem jawnym (z bardzo dużym prawdopodobieństwem, w idealnym przypadku z pewnością). Ludzie mogą wyraźnie rozpoznać zły tekst, po prostu na niego patrząc. Implementacja tej zdolności w komputerach należy do dziedziny sztucznej inteligencji. Jednak większość współczesnych metod AI (np. sieci neuronowe) wydaje się być zbyt wolna, aby można ją było zastosować na tym etapie algorytmu siłowego, ponieważ każdy tekst musi zostać oceniony za pomocą tego predykatu. Większość metod szybkiego filtrowania tekstu negatywnego opiera się na zabronionych n-gramach. Jako n-gram rozważalibyśmy tylko sekwencję n kolejnych liter. Jeśli rozmiar alfabetu wynosi N, możliwe jest utworzenie Nⁿ możliwych n-gramów. W przypadku wyższego n tylko niewielka ich część może pojawić się w prawidłowym tekście w danym języku. Korzystając z drzewa leksykalnego lub tabeli wyszukiwania, można łatwo (i szybko) sprawdzić, czy dany n-gram jest prawidłowy, czy nie. Tak więc naturalnym testem jest sprawdzenie każdego n-gramu w tekście, czy jest poprawny, czy nie. Istnieją dwa podstawowe problemy wynikające z tego podejścia - prawdziwy tekst jawny może zawierać (umyślnie) błędnie napisane, nietypowe lub obce słowa, a zatem nasza baza danych n-gramów może być niekompletna. Możemy ograniczyć nasz test do pewnych określonych wzorców, np. zbyt długiego ciągu następujących po sobie samogłosek/spółgłosek. Wzorce te można sprawdzić w czasie zależnym od długości kandydata tekstu jawnego. Filtr może również opierać się na sprawdzaniu tylko kilku n-gramów w ustalonej lub losowej pozycji w tekście, np. pierwszych czterech literach. Reguła odrzucania tekstów powinna opierać się na dokładnym typie szyfru, który próbujemy rozszyfrować. Na przykład, jeśli pierwsze cztery litery odszyfrowanego tekstu jawnego nie zależą od jakiejś części klucza, filtr oparty tylko na ich poprawności nie będzie skuteczny. Interesującym pytaniem jest, czy możliwe jest stworzenie systemu, który może skutecznie uczyć się swoich reguł filtrowania z istniejących odszyfrowanych tekstów, nawet w procesie odszyfrowywania.

Funkcje punktacji

Dzięki krokowi negatywnego filtra możemy wyeliminować około 90% lub więcej tekstów kandydackich. Liczba tekstów do zweryfikowania jest nadal bardzo duża, dlatego musimy zastosować bardziej precyzyjne metody rozpoznawania tekstu jawnego. Używamy funkcji punktacji, która przypisuje wartość - wynik - każdemu tekstowi, który przetrwał eliminację w poprzednich krokach. Tutaj wyższy wynik oznacza większe prawdopodobieństwo, że dany tekst jest prawidłowym tekstem jawnym. Dla każdej funkcji punktacji możemy przypisać próg i powinno być bardzo mało prawdopodobne, aby prawidłowy tekst jawny miał wynik poniżej tego progu. Rzeczywistą wartość progową można znaleźć albo eksperymentalnie (poprzez ocenę dużej liczby rzeczywistych tekstów), albo może być oparta na analizie statystycznej. Szybkość funkcji punktacji można określić, używając klasycznych szacunków złożoności algorytmu. Precyzję punktacji można zdefiniować za pomocą rozdzielenia prawidłowych i nieprawidłowych tekstów jawnych. Istnieje kompromis związany z punktacją, ponieważ szybsze funkcje punktacji są mniej precyzyjne i odwrotnie. Dlatego stosujemy dwie funkcje punktacji: jedną, która jest szybka, ale mniej precyzyjna, z niższą wartością progową, i jedną, która jest bardzo precyzyjna, ale trudniejsza do obliczenia. Przykład rozkładów funkcji punktacji można znaleźć na poniższych rysunkach.





Funkcja punktacji na rysunku pierwszym jest znacznie dokładniejsza niż na rysunku drugim, ale czas obliczeniowy wymagany do oceny jest podwojony. Co więcej, funkcja punktacji na rysunku pierwszym została utworzona ze zmniejszonego słownika dopasowanego do danego szyfrogramu. Ocena oparta na kompletnym słowniku jest wolniejsza, trudniejsza do wdrożenia i może być nawet mniej precyzyjna. Funkcje punktacji mogą być oparte na słowach słownikowych, statystykach n-gramów lub innych konkretnych statystykach. Trudno jest zapewnić uniwersalną funkcję punktacji, ponieważ proces deszyfrowania dla różnych typów szyfrów ma wpływ na rzeczywiste wyniki funkcji punktacji. Np. podczas próby odszyfrowania szyfru transpozycyjnego wiemy już, które litery pojawiają się z jaką częstotliwością, a zatem statystyki oparte na częstotliwości liter nie odgrywają żadnej roli w punktacji. Z drugiej strony są one dość znaczące dla szyfrów podstawieniowych. Najczęstsze uniwersalne funkcje punktacji to :

1. Liczba słów słownikowych w tekście / ułamek znaczącego tekstu. Punktacja oparta na słowach słownikowych jest bardzo precyzyjna, jeśli mamy wystarczająco duży słownik. Nawet jeśli nie każde słowo w ukrytej wiadomości znajduje się w naszym słowniku, jest bardzo mało prawdopodobne, że jakieś nieprawidłowe odszyfrowanie zawiera większą część tekstu złożoną ze słów słownikowych. Usunięcie krótkich słów ze słownika może zwiększyć precyzję. Inną możliwością jest użycie wag opartych na długości słowa. Słowa słownikowe można znaleźć za pomocą drzew leksykalnych. W niektórych językach powinniśmy używać słownika rdzeni słów, zamiast całych słów. Szybkość oceny zależy odpowiednio od długości tekstu i średniej długości słów w słowniku.
2. Odległość rangowa n-gramów. Ranga n-gramu to jego pozycja zależna od kolejności opartej na częstościach n-gramów (połączona dla wszystkich n do danej granicy zależnej od języka). Ta metoda jest stosowana w szybkim automatycznym rozpoznawaniu języka: obliczanie rang n-gramów danego tekstu i porównywanie ich z rangami znaczących n-gramów uzyskanymi z dużego korpusu różnych języków. Poprawny język powinien mieć najmniejszą odległość. Nawet jeśli tę metodę można dostosować do rozpoznawania tekstu jawnego, np. poprzez tworzenie "losowego" korpusu lub korpusu zaszyfrowanego, nie wydaje się to praktyczne.
3. Częstotliwość odległości statystyk n-gramowych. Wynik tekstu można oszacować na podstawie różnicy zmierzonej częstości n-gramów i szacowanych częstości z dużego korpusu. Zakładamy, że poprawny tekst jawny będzie miał najmniejszą odległość od statystyk korpusowych. Jednak ze względu na właściwości statystyczne tekstu nie zawsze jest to prawdą w przypadku krótkich lub szczegółowych tekstów. Dlatego precyzja tej funkcji punktacji jest wyższa w przypadku dłuższych tekstów. Szybkość oceny zależy od rozmiaru tekstu i rozmiaru n.
4. Tabele punktacji dla n-gramów. Jeśli weźmiemy pod uwagę statystyki wszystkich n-gramów, zobaczymy, że większość n-gramów wnosi bardzo małą wartość do końcowego wyniku. Możemy wziąć pod uwagę wkład tylko najpopularniejszych n-gramów. Dla danego języka (i danego szyfrogramu) możemy przygotować tabelę wyników n-gramów ze stałą liczbą wpisów. Wynik jest oceniany jako suma punktów przypisanych do n-gramów w danym tekście kandydackim. Możemy przypisać zarówno dodatnie wyniki dla typowych prawidłowych n-gramów, jak i ujemne wyniki dla typowych nieprawidłowych/rzekomo rzadkich n-gramów. Jednak precyzja tej metody jest bardzo niska, szczególnie w przypadku szyfrów transpozycyjnych. W naszych eksperymentach wyniki mają rozkład normalny, a zazwyczaj poprawny tekst jawny nie ma najwyższych możliwych wartości. Z drugiej strony, ta funkcja punktacji jest łatwa do oceny i może być dostosowana do danego szyfrogramu. Dlatego może być używana jako szybka funkcja punktacji fastScore(X). 5. Wskaźnik koincydencji (i inne podobne statystyki) Wskaźnik koincydencji, oznaczony jako IC, jest odpowiednią i szybką statystyką stosowaną do szyfrów, które modyfikują częstotliwość występowania liter. Pojęcie to pochodzi z prawdopodobieństwa wystąpienia tej samej litery w dwóch różnych tekstach w tej samej pozycji. Zaszyfrowane teksty są uważane za losowe i mają (znormalizowany) wskaźnik koincydencji bliski 1,0. Z drugiej strony, tekst jawny ma znacznie wyższy IC w pobliżu wartości oczekiwanej dla danego języka i alfabetu. Dla języka angielskiego oczekiwana wartość wynosi 1,73. Jak w przypadku wszystkich statystyk opartych na funkcji punktacji, jej precyzja jest zależna od długości tekstu. Wskaźnik koincydencji jest najbardziej odpowiedni dla szyfrów polialfabetycznych, w których szyfrowanie zależy od położenia litery w tekście (np. szyfr Vigenère′a). Można go dostosować do innych typów szyfrów, np. do szyfrów transpozycyjnych, biorąc pod uwagę, że alfabet jest tworzony przez wszystkie możliwe n-gramy z pewnym n > 1.

PRZYSZŁE TRENDY

Przetwarzanie i rozpoznawanie języka mają zastosowanie w różnych obszarach poza kryptoanalizą (OCR, automatyczne tłumaczenie). Niektóre techniki kryptoanalityczne można uogólnić dla tych dziedzin. Np. niektóre litery lub grupy liter są często zastępowane innymi w zeskanowanych dokumentach. W związku z tym korygowanie tych dokumentów jest podobne do kryptoanalizy szyfrów podstawieniowych. Dzięki badaniom nad sztuczną inteligencją można uzyskać nowe spostrzeżenia na temat struktury języka naturalnego, które mogą pomóc w dalszej kryptoanalizie. Kryptoanaliza jest również ściśle związana z wysiłkami automatycznego tłumaczenia. Niektóre otwarte problemy, które muszą zostać rozwiązane przez rozpoznawanie języka odpowiednie do kryptoanalizy klasycznych szyfrów, to:

•  W jaki sposób rozpoznawanie tekstu powinno być zintegrowane z procesem deszyfrowania, aby zapewnić sprzężenie zwrotne, np. w przypadku częściowo odszyfrowanych słów, oszacować nowy klucz itp. Jest to szczególnie ważne, jeśli użyjemy bardziej zaawansowanej heurystyki wyszukiwania niż wyszukiwanie siłowe w przestrzeni kluczy.
•  W jaki sposób składnia i semantyka języka mogą pomóc w rozpoznawaniu tekstu i wyszukiwaniu kluczy.
•  W jaki sposób różne kodowania i systemy pisma wpływają na kryptoanalizę. Specyficzne problemy pojawiają się przy pracy z różnymi systemami pisma .
•  Jak prawidłowo rozpoznawać tekst z celowymi błędami ortograficznymi i specjalnymi słowami kodowymi.

Inny zestaw problemów pojawia się, gdy używane są różne języki naturalne, takie jak rozpoznawanie języka, określone alfabety, wpływ znaków diakrytycznych itp. Nasze badania pokazują, że język wiadomości zaszyfrowanej szyfrem podstawieniowym można rozpoznać nawet bez deszyfrowania. Możliwe jest nawet użycie słownika innego (choć podobnego) języka w procesie deszyfrowania. Interesującym pytaniem badawczym jest to, czy możliwe jest stworzenie całkowicie ogólnej funkcji rozpoznawania języka (lub ograniczonej do pewnej rodziny języków) nadającej się do kryptoanalizy. Rozpoznawanie tekstu jawnego w kryptoanalizie można również postrzegać jako specyficzny problem wyszukiwania informacji . Wyszukiwanie informacji wielojęzycznych ma na celu podobne problemy do problemów przedstawionych powyżej . Badania w tych obszarach mogą wyraźnie na siebie wpływać w przyszłości.

WNIOSEK

W tym artykule podsumowano wykorzystanie i ograniczenia przetwarzania języka w kontekście kryptoanalizy klasycznych szyfrów. Ich zastosowanie zwykle różni się w zależności od charakteru analizowanych systemów szyfrów, chociaż przedstawiliśmy kilka typowych technik, które można łatwo dostosować do konkretnej sytuacji. Większość ataków kryptoanalitycznych wymaga bardzo szybkiego rozpoznawania języka, ale z drugiej strony duża prędkość często powoduje niedokładne wyniki, aż do punktu nierozpoznawalnych odszyfrowań. Rolą badań nad sztuczną inteligencją jest znajdowanie szybszych i bardziej precyzyjnych predykatów językowych i łączenie ich w użyteczny system rozpoznawania tekstu jawnego. Do zrobienia!

WSTĘP

Klasyczne szyfry służą do szyfrowania wiadomości tekstowych zapisanych w języku naturalnym w taki sposób, że są one czytelne tylko dla nadawcy lub zamierzonego odbiorcy. Wiele klasycznych szyfrów można złamać metodą siłowego przeszukiwania przestrzeni klucza. Metody sztucznej inteligencji, takie jak heurystyka optymalizacyjna, można wykorzystać do zawężenia przestrzeni wyszukiwania, przyspieszenia przetwarzania tekstu i rozpoznawania tekstu w procesie kryptoanalizy. Przedstawiamy tutaj szeroki przegląd różnych technik AI, które można wykorzystać w kryptoanalizie klasycznych szyfrów. W następnej części Zautomatyzowana kryptoanaliza - Przetwarzanie języka omówiono konkretne metody skutecznego rozpoznawania prawidłowo odszyfrowanego tekstu spośród wielu możliwych odszyfrowanych.

TŁO

Kryptoanalizę można postrzegać jako próbę przetłumaczenia tekstu zaszyfrowanego (zaszyfrowanego tekstu) na język ludzki. Kryptoanalizę można zatem powiązać z lingwistyką obliczeniową. Obszar ten powstał w wyniku wysiłków podejmowanych w Stanach Zjednoczonych w latach 50. XX wieku, aby komputery automatycznie tłumaczyły teksty z języków obcych na angielski, w szczególności rosyjskie czasopisma naukowe. Obecnie jest to dziedzina badań poświęcona opracowywaniu algorytmów i oprogramowania do inteligentnego przetwarzania danych językowych. Systematyczne (publiczne) wysiłki na rzecz automatyzacji kryptoanalizy przy użyciu komputerów można prześledzić do pierwszych prac napisanych pod koniec lat 70. Jednak obszar badań nadal ma wiele otwartych problemów, ściśle związanych z obszarem sztucznej inteligencji. Z obecnego stanu wiedzy można wnioskować, że chociaż komputery są bardzo przydatne w wielu zadaniach kryptoanalitycznych, ludzka inteligencja jest nadal niezbędna w kompletnej kryptoanalizie. Dla wygody czytelnika przypominamy kilka podstawowych pojęć z kryptografii. Bardzo dokładny przegląd klasycznych szyfrów został napisany przez Kahna (1974). Wiadomość do zaszyfrowania (tekst jawny) jest napisana małymi literami P = {a, b, c… x, y, z}. Zaszyfrowana wiadomość (tekst szyfrowany) jest napisana wielkimi literami alfabetu C = {A, B, C… X, Y, Z}. Różne alfabety są używane w celu lepszego odróżnienia tekstu jawnego od tekstu szyfrowanego. W rzeczywistości te alfabety są takie same. Istnieje odwracalna reguła szyfrowania (algorytm), jak przekształcić tekst jawny w tekst szyfrowany i odwrotnie. Algorytmy te zależą od tajnego parametru K zwanego kluczem. Zestaw możliwych kluczy K nazywany jest przestrzenią kluczy. Dane wejściowe i wyjściowe tych algorytmów to ciąg liter z odpowiednich alfabetów, P^* i C^*. Zarówno nadawca, jak i odbiorca używają tego samego tajnego klucza i tych samych algorytmów szyfrowania i deszyfrowania. Istnieją trzy podstawowe klasyczne systemy szyfrowania wiadomości, a mianowicie podstawienie, transpozycja i klucz bieżący. W szyfrze podstawieniowym ciąg liter jest zastępowany innym ciągiem liter przy użyciu przepisanej substytucji pojedynczych liter, np. od lewej "a" do "A", zastępując literę "b" literą "N", literę "c" literą "G" itd. Szyfr transpozycyjny zmienia kolejność liter zgodnie z tajnym kluczem K. W przeciwieństwie do szyfrów podstawieniowych częstotliwość liter w tekście jawnym i szyfrogramie pozostaje taka sama. Ta cecha jest wykorzystywana do rozpoznawania, że tekst został zaszyfrowany przez jakiś szyfr transpozycyjny. Typowy szyfr z kluczem bieżącym polega na wyprowadzeniu z klucza głównego K klucza bieżącego K₀ K₁ K₂ …K_n. Jeśli P = C = K jest grupą, to po prostu y_i = e_K( x_i) = x_i + K_i . Dlatego wygodnie jest zdefiniować algorytm szyfrowania dla szyfrów klasycznych w następujący sposób:

Definicja 1: Klasyczny system szyfrów to pięciokrotność (P, C, K, E, D), gdzie spełnione są następujące warunki:

1. P jest skończonym zbiorem alfabetu tekstu jawnego, a P^* zbiorem wszystkich skończonych ciągów symboli z P.
2. C jest skończonym zbiorem alfabetu szyfrogramu, a C^* zbiorem wszystkich skończonych ciągów symboli z C
3. K jest skończonym zbiorem możliwych kluczy.
4. Dla każdego K ∈ K istnieje algorytm szyfrowania e_K ∈ E i odpowiadający mu algorytm deszyfrowania d_K ∈ D taki, że d_K (e_K(x)) = x dla każdego wejścia x ∈ P i K ∈ K.
5. Algorytm szyfrowania przypisuje dowolnemu skończonemu ciągowi x₀ x₁ x₂…x_n z P^* wynikowy ciąg szyfrogramu y₀ y₁ y₂…y_n z C^*, gdzie y_i = e_K(x_i) . Rzeczywisty klucz może lub nie musi zależeć od indeksu i.

Innym typowym przypadkiem dla P i C są r-krotności alfabetu łacińskiego. W przypadku szyfrów transpozycyjnych klucz jest okresowo powtarzany dla r-krotności. W przypadku szyfrów podstawieniowych r-krotności kluczem jest r-krotność kluczy. W przypadku kluczy bieżących istnieje inny generator strumienia kluczy g: K × P → K, który generuje z początkowego klucza K i ewentualnie z tekstu jawnego x₀ x₁ x₂&hellup;…x_n-1 rzeczywisty klucz K_n . W przypadku szyfrów klasycznych występują dwie typowe sytuacje, gdy próbujemy odzyskać tekst jawny:

1. Niech dane wejściowe do algorytmu deszyfrującego d_K ∈ D z nieznanym kluczem K będą ciągiem tekstu zaszyfrowanego y₀ y_1K y₂ …y_nn z C^*, gdzie y_i = e_K( x_i). Naszym celem jest znalezienie ciągu tekstu jawnego x₀ x₁ x₂…x_n z P^*. Tak więc w każdym wykonaniu algorytm przeszukuje przestrzeń kluczy K.

2. Algorytm deszyfrowania d_K ∈ D i klucz K są nieznane. Naszym celem jest 2nalezienie dla ciągu szyfrogramu y₀ y₁ y₂&hellup;y_nK z C^*, gdzie yⁱ = e_K( x_i), ciągu jawnego tekstu x₀ x₁ x₂…x_n z P^*. Wymaga to innego algorytmu niż rzeczywisty d_K ∈ D, a także pewnych dodatkowych informacji. Zwykle dostępny jest inny szyfrogram, powiedzmy z₀ z₁ z_2K…z_n z C^*. Tak więc w każdym wykonaniu algorytm przeszukuje możliwe podstawienia, które są odpowiednie dla obu szyfrogramów.

W obu przypadkach potrzebujemy podprogramu rozpoznawania tekstu jawnego, który ocenia kandydacki podciąg o długości v dla możliwego tekstu jawnego, powiedzmy c_t c_1+t c_2+t …c_+t := x_t x_1+t x_2+t…x_v+t . Takie automatyczne rozpoznawanie tekstu wymaga odpowiedniego modelu używanego języka.

AUTOMATYCZNA KRYPTANALIZA

Istnieją dwie proste metody automatycznej kryptoanalizy. Niestety, żadna z nich nie nadaje się do dłuższych ciągów znaków w praktyce. Pierwsza z nich dotyczy szyfrów transpozycyjnych. Gdy nie są znane żadne inne informacje o szyfrze, możemy użyć ogólnej metody, zwanej anagramowaniem, aby rozszyfrować wiadomość. W tej metodzie próbujemy złożyć sensowny ciąg znaków (anagram) z szyfrogramu. Osiąga się to poprzez ułożenie liter w słowa ze słownika. Gdy znajdziemy sensowne słowo, przetwarzamy resztę wiadomości w ten sam sposób. Gdy nie jesteśmy w stanie utworzyć bardziej sensownych słów, cofamy się i próbujemy innych możliwych słów, aż znajdziemy cały sensowny anagram. Druga, bardzo podobna, metoda dotyczy szyfrów podstawieniowych. Tutaj próbujemy złożyć sensowny ciąg znaków (anagram) z szyfrogramu, przeszukując wszystkie możliwe podstawienia liter, aby uzyskać słowa ze słownika używanego języka. Chociaż rozmiar przestrzeni klucza jest duży, automatyczna kryptoanaliza wykorzystuje wiele innych metod opartych np. na rozkładzie częstości liter. Automatyczna kryptoanaliza prostych szyfrów podstawieniowych może odszyfrować większość wiadomości zarówno ze znanymi granicami słów , jak i bez tych informacji . Istnieją inne klasyczne szyfry, w których transpozycja lub podstawienie zależy nie tylko od rzeczywistego klucza, ale także od pozycji w bloku liter ciągu. Do skutecznej automatycznej kryptoanalizy wymagane są co najmniej dwie warstwy przetwarzania kandydatów w postaci jawnego tekstu, filtrowania i punktowania. Lepsze wyniki uzyskuje się poprzez dodatkowe warstwy filtrujące. To oczywiście zwiększa złożoność obliczeniową. Poniżej przedstawiamy przegląd tych warstw filtrujących.

Zautomatyzowane ataki siłowe

Podstawowym typem algorytmu nadającego się do zautomatyzowanej kryptoanalizy jest atak siłowy. Ponieważ musimy przeszukać całą przestrzeń kluczy, ten atak jest wykonalny tylko wtedy, gdy przestrzeń kluczy nie jest "zbyt duża". Dokładne określenie ilościowe przeszukiwalnej przestrzeni kluczy zależy od zasobów obliczeniowych dostępnych dla atakującego i średniego czasu potrzebnego do weryfikacji kandydata na odszyfrowany tekst. Zatem rozpoznawanie tekstu jawnego jest najważniejszą częścią algorytmu z punktu widzenia wydajności. Z drugiej strony, tylko najbardziej złożone algorytmy osiągają naprawdę wysoką dokładność rozpoznawania tekstu jawnego. Dlatego też wymagana jest ostrożna równowaga między złożonością algorytmów rozpoznawania tekstu jawnego a jego dokładnością. Jest mało prawdopodobne, aby zautomatyzowana kryptoanaliza dawała tylko jeden możliwy wynik, ale możliwe jest ograniczenie zestawu możliwych odszyfrowania do rozmiaru, który można opanować. Zgłoszone wyniki powinny być sortowane według prawdopodobieństwa, że są prawdziwym tekstem jawnym. Zidentyfikowaliśmy trzy warstwy rozpoznawania tekstu jawnego, a mianowicie negatywny predykat testowy, szybką funkcję punktacji i precyzyjną funkcję punktacji. Wszystkie trzy funkcje są używane jako filtr trójwarstwowy, a ostateczna funkcja punktacji jest również używana do sortowania wyników. Pierwszy filtr powinien być bardzo szybki i powinien mieć bardzo niskie prawdopodobieństwo błędu. Szybki wynik powinien być łatwy do obliczenia, ale nie jest wymagany do precyzyjnej identyfikacji poprawnego tekstu jawnego. Poprawne rozpoznawanie tekstu jawnego jest rolą precyzyjnej funkcji punktacji. W algorytmie najlepszy wynik jest najwyższy. Jeśli wynik jest obliczany w przeciwnym znaczeniu, algorytm musi zostać odpowiednio przepisany. W niektórych przypadkach możemy zintegrować szybką funkcję punktacji w negatywnym teście lub z precyzyjną punktacją, co prowadzi do filtrów dwuwarstwowych. Możliwe jest również użycie jeszcze większej liczby kroków filtrowania opartego na predykatach i wynikach. Jednak eksperymenty pokazują, że proponowana architektura trzech warstw jest najbardziej elastyczna, a więcej warstw może nawet prowadzić do spadku wydajności.

Zastosowania metod sztucznej inteligencji

Metody sztucznej inteligencji (AI) można stosować w czterech głównych obszarach zautomatyzowanej kryptoanalizy:

1. Rozpoznawanie tekstu jawnego: Celem AI jest dostarczanie predykatów negatywnych, które filtrują błędne odszyfrowania, oraz funkcji punktacji, które oceniają podobieństwo tekstu do języka naturalnego.
2. Heurystyka wyszukiwania klucza: Celem AI jest dostarczanie heurystyk w celu przyspieszenia procesu odszyfrowywania, albo poprzez ograniczenie przestrzeni klucza, albo poprzez kierowanie wyborem kolejnych kluczy do wypróbowania w odszyfrowaniu. Ten obszar jest najczęściej badany, ponieważ może dostarczyć jasnych wyników eksperymentalnych i znaczącej oceny.
3. Oszacowanie tekstu jawnego: Celem AI jest oszacowanie znaczenia tekstu jawnego na podstawie częściowego odszyfrowania lub oszacowanie niektórych części tekstu jawnego na podstawie danych zewnętrznych (np. nadawcy szyfrogramu, kontekstu historycznego i geograficznego, określonych reguł gramatycznych itp.). Oszacowane części tekstu jawnego mogą następnie prowadzić do znacznie łatwiejszego całkowitego odszyfrowania. Ten obszar badań jest w większości niezbadany, a oszacowanie tekstu jawnego jest wykonywane przez kryptoanalityka.
4. Automatyczna ocena bezpieczeństwa: Celem kryptoanalizy jest nie tylko łamanie szyfrów i poznawanie sekretów, ale jest ona również wykorzystywana podczas tworzenia nowych szyfrów w celu oceny ich bezpieczeństwa. Chociaż większość klasycznych szyfrów jest już "przestarzała", ich kryptoanaliza jest nadal ważna, np. w nauczaniu nowoczesnych zasad bezpieczeństwa komputerowego. Podczas nauczania klasycznych szyfrów przydatne jest posiadanie narzędzia AI (np. systemu eksperckiego), które może zautomatyzować ocenę bezpieczeństwa szyfru (przynajmniej przy niektórych słabszych założeniach). Chociaż włożono wiele pracy w automatyczną ocenę nowoczesnych protokołów bezpieczeństwa, nie znamy niektórych narzędzi służących do oceny projektów "klasycznych" szyfrów.

Obszarem, który najlepiej jest zbadać, jest obszar heurystyki wyszukiwania kluczy. Wynika to bezpośrednio z faktu, że przeszukiwanie metodą siłową całej przestrzeni kluczy można uznać za bardzo prymitywną metodę deszyfrowania. Większość klasycznych szyfrów nie została zaprojektowana z uwzględnieniem statystyk tekstu. Możemy przypisać wynik dla każdego klucza w przestrzeni kluczy, który jest skorelowany z prawdopodobieństwem, że tekst odszyfrowany danym kluczem jest tekstem jawnym. Wynik, gdy jest rozpatrywany w przestrzeni kluczy, z pewnością ma pewne lokalne maksima, które mogą prowadzić bezpośrednio do sensownego tekstu jawnego lub tekstu, z którego tekst jawny jest łatwo odgadnięty. Dlatego może być przydatne rozważenie różnych technik relaksacyjnych w celu przeszukiwania przestrzeni kluczy w celu maksymalizacji funkcji punktacji. Jedną z najwcześniejszych demonstracji technik relaksacyjnych w celu złamania szyfrów podstawieniowych przedstawili Peleg & Rosenfeld (1979) oraz Hunter & McKenzie (1983). Udane ataki mające zastosowanie do wielu klasycznych szyfrów mogą być implementowane przy użyciu podstawowego wspinania się na wzgórze, poprzez przeszukiwanie tabu, symulowane wyżarzanie i zastosowania algorytmów genetycznych/ewolucyjnych. Algorytmy genetyczne osiągnęły wiele sukcesów w łamaniu klasycznych szyfrów, jak zademonstrowali Mathews (1993) lub Clark (1994), i mogą nawet złamać maszynę wirnikową. Russell, Clark & Stepney (1998) przedstawiają atak anagramowy przy użyciu rozwiązywacza opartego na algorytmie optymalizacji kolonii mrówek. Tego typu ataki próbują zbiec do poprawnego klucza poprzez małe zmiany rzeczywistego klucza. Współczynnik powodzenia ataków jest zwykle mierzony ułamkiem zrekonstruowanego klucza i/lub tekstu. Metody relaksacyjne mogą z dużym prawdopodobieństwem znaleźć klucze lub przybliżenia tekstu jawnego, nawet jeśli nie jest wykonalne przeszukanie całej przestrzeni kluczy. Sukces zależy głównie od rozmiaru szyfrogramu, ponieważ punktacja jest zwykle oparta na statystykach. Jednym z niezbadanych wyzwań jest rozważenie zastosowania wielu technik relaksacji. Po pierwsze, można użyć heurystyki, aby zmniejszyć przestrzeń klucza, a następnie albo brutalne wyszukiwanie, albo inna heurystyka jest używana z większą precyzją, aby zakończyć odszyfrowanie.

TRENDY PRZYSZŁOŚCI

Uzyskane wyniki w dużym stopniu zależą od rozmiaru szyfrogramu, a odszyfrowania są zwykle tylko częściowe. Techniki automatycznej kryptoanalizy muszą być również dopasowane do danego problemu. Np. ataki na szyfry podstawieniowe mogą wykorzystywać statystyki pojedynczych liter, ale w przypadku ataków przeznaczonych na szyfry transpozycyjne statystyki te są niezmienne i nie mają sensu ich stosowanie. Zautomatyzowana kryptoanaliza jest zwykle badana tylko w kontekście tych dwóch głównych typów szyfrów, ale istnieje szeroki obszar niezbadanych problemów dotyczących różnych klasycznych typów szyfrów, takich jak uruchamianie szyfrów typu klucza. Konkretne zastosowania technik AI mogą zawieść w przypadku niektórych kryptosystemów, jak wskazali Wagner, S., Affenzeller, M. i Schragl, D. (2004). Kryptoanaliza zależy również od języka , chociaż istnieją pewne godne uwagi wyjątki, jeśli chodzi o podobne języki. Wraz ze wzrostem mocy obliczeniowej, nawet niedawno używane szyfry, takie jak Data Encryption Standard (DES), stają się przedmiotem zautomatyzowanej kryptoanalizy. Oprócz zastosowania heurystyki do kryptoanalizy, konieczne są dalsze badania w obszarach szacowania tekstu jawnego i automatycznej oceny bezpieczeństwa. System ekspercki, który obejmowałby te obszary i łączył je ze sztuczną inteligencją do rozpoznawania tekstu jawnego i heurystyki wyszukiwania, może być silnym narzędziem do nauczania bezpieczeństwa komputerowego lub do pomocy w analizie kryminalistycznej lub badaniach historycznych obejmujących zaszyfrowane materiały.

WNIOSEK

Niniejszy artykuł dotyczy zautomatyzowanej kryptoanalizy klasycznych szyfrów, gdzie klasyczne szyfry są uważane za szyfry sprzed II wojny światowej lub szyfry ołówkowo-papierowe. Heurystyki optymalizacyjne są dość skuteczne w atakach na te szyfry, ale zazwyczaj nie można ich w pełni zautomatyzować. Ich zastosowanie zazwyczaj różni się w zależności od charakteru analizowanych systemów szyfrów. Ważnym kierunkiem badań jest rozszerzenie technik od klasycznej kryptoanalizy do zautomatyzowanego deszyfrowania nowoczesnych cyfrowych kryptosystemów. Innym ważnym problemem jest stworzenie zestawu w pełni zautomatyzowanych narzędzi kryptoanalitycznych lub kompletnego systemu eksperckiego, który można dostosować do różnych typów szyfrów i języków.

WSTĘP

Obecnie systemy informatyczne (IS) są projektowane z myślą o kontroli realizacji poszczególnych zadań, umożliwiając koordynację, monitorowanie i wspieranie logistycznych aspektów procesu biznesowego. Innymi słowy, system informatyczny musi zarządzać przepływem pracy w organizacji. Zarządzanie przepływem pracy stanowi kluczowy element dla osiągnięcia konkurencyjności przedsiębiorstwa. Wiele firm zdało sobie sprawę, że procesy biznesowe (BP) w ich organizacjach oraz między firmami a ich partnerami nie zostały jasno opisane i brakuje technik i metod automatyzacji tych procesów. Koalicja ds. Zarządzania Przepływem Pracy (WFMC) stwierdza, że przepływ pracy (WF) dotyczy automatyzacji procedur, w których dokumenty, informacje lub zadania są przekazywane uczestnikom zgodnie z określonym zestawem reguł w celu osiągnięcia lub przyczynienia się do osiągnięcia ogólnego celu biznesowego . Inną definicję WF można znaleźć w pracy , gdzie przepływy pracy to działania obejmujące skoordynowane wykonywanie wielu zadań przez różne podmioty przetwarzające (osoby lub maszyny). Zadanie lub proces obejmuje element pracy i podmiot procesu, który wykonuje tę pracę. Zarządzanie przepływem pracy (WFM) to szybko rozwijająca się technologia, która jest coraz częściej wykorzystywana przez firmy z różnych branż. Jej główną cechą jest automatyzacja procesów obejmujących kombinację działań ludzkich i maszynowych .System zarządzania przepływem pracy (WFMS) zapewnia proceduralną automatyzację procesu biznesowego poprzez zarządzanie sekwencją działań i angażowanie odpowiednich zasobów ludzkich i/lub informatycznych związanych z poszczególnymi etapami działania. Chociaż najpowszechniejszym zastosowaniem WFMS jest środowisko biurowe, w którym intensywnie pracują pracownicy, takie jak ubezpieczenia, bankowość, usługi prawne i administracja ogólna, można go również znaleźć w niektórych rodzajach aplikacji przemysłowych i produkcyjnych . WFMS wymaga integracji innych technologii, takich jak technologia agentów, która zapewnia elastyczne, rozproszone i inteligentne rozwiązania do zarządzania procesami biznesowymi. Niniejsza praca przedstawia metodologię rozwoju WFMS opartego na agentach mobilnych. Proponowana metodologia polega na modułowej i stopniowej specyfikacji systemu, w której agent mobilny kieruje procesem przez jednostki organizacyjne i wykonuje różne zadania. W systemie ewoluuje kilku agentów mobilnych, wykonując jednocześnie przypisane im zadania.

TŁO

Zarządzanie przepływem pracy

Pojęcie agenta jest używane jako "system komputerowy umieszczony w pewnym środowisku, który jest zdolny do autonomicznego działania w tym środowisku w celu osiągnięcia swoich celów projektowych" . Prace te podkreślają również korzyści płynące z zastosowania technologii agentów w zarządzaniu procesami biznesowymi; niektóre z tych korzyści to: rozproszona architektura systemu, wrodzona autonomia agentów programowych, ponieważ agenci mogą uruchamiać proces roboczy (WF) w oparciu o wyzwalacz zdarzenia, reaktywność agenta, ponieważ ma on zdolność generowania alternatywnych ścieżek wykonania itp. Inteligentny agent jest zdolny do autonomicznego działania i elastycznego zachowania w celu osiągnięcia swoich celów projektowych, a także posiada cechy reaktywności, proaktywności i zdolności społecznych. W innych pracach obie koncepcje są zintegrowane. W pracy przedstawiono metodologię projektowania procesów roboczych opartych na agentach (WF); składała się ona z trzech kroków. W pierwszym kroku autorzy modelują proces roboczy (BP) za pomocą diagramów aktywności UML, identyfikując wszystkie niezbędne zasoby i czynności. W drugim kroku wszystkie czynności identyfikujące role w równoległych ścieżkach są grupowane. Na koniec definiują agenta dla każdej grupy. Wielu badaczy wykorzystało technologię agentów do ulepszenia aplikacji WF. Zaproponowano architekturę zaawansowanych procesów roboczych opartych na agentach. W oparciu o tę architekturę rozbijają oni wykonywanie procesów roboczych (WF) i sterowanie przepływem procesów na małe jednostki wykonawcze obsługiwane przez inteligentnych agentów, a procesy WF są kontrolowane w sposób zdecentralizowany. Podejście oparte na współpracy w systemach przepływu pracy przedstawiono w pracy Savarimuthu i Purvis, 2004, gdzie agenci współpracują, tworząc sieci społecznościowe (społeczności). W pracy Savarimuthu, Purvis i Fleurke, 2004 agenci są osadzeni w systemie, który może monitorować i kontrolować ogólne funkcjonowanie procesu przepływu pracy w systemie WF opartym na agentach. W pracy Minhong, Huaiquing i Dongming, 2005technologia agentów jest wykorzystywana do monitorowania WF, gdzie różni inteligentni agenci współpracują ze sobą, aby wykonywać elastyczne zadania monitorowania w sposób autonomiczny i zespołowy.

Systemy wieloagentowe

Agenci mobilni to autonomiczne programy, które mogą przemieszczać się z jednego komputera na drugi pod własną kontrolą. Oferują one solidne i wydajne środowisko do tworzenia aplikacji rozproszonych, w tym aplikacji mobilnych. Agent stacjonarny jest uruchamiany tylko w systemie, w którym rozpoczął działanie. Jeśli potrzebuje informacjiz innego systemu lub musi wejść w interakcję z innym agentem, korzysta ze standardowej komunikacji klient-serwer (RMI, RPC, CORBA). Agent mobilny (MA) nie zawsze jest przyłączony do systemów, w których rozpoczyna wykonywanie, lecz jest w stanie samodzielnie przemieszczać się przez węzły sieciowe, w których jest to dozwolone, modyfikując ostatecznie swoje środowisko wykonawcze; MA przenosi ze sobą swój aktualny stan i kod (duża mobilność). Ponadto, MA mogą wykazywać szereg korzystnych cech wynikających z mobilności, na przykład a) interakcję z zasobem podczas jego migracji do potrzebnej lokalizacji, zachowując przepustowość i zmniejszając opóźnienie sieci interakcję z użytkownikami podczas migracji do lokalizacji użytkownika, odpowiadając szybciej na żądania użytkowników. W obu przypadkach agent kontynuuje interakcję z zasobem lub użytkownikiem nawet w przypadku tymczasowych awarii połączeń sieciowych. Większość aplikacji rozproszonych naturalnie wpisuje się w model MA, ponieważ agenci mogą migrować sekwencyjnie przez sieć komputerową, wysyłają innych agentów do równoległej wizyty na komputerach, pozostają stacjonarni i wchodzą w interakcje ze zdalnymi zasobami itp. Istnieje wiele organizacji, których celem jest ustanowienie standardów rozwoju oprogramowania agentów i ich interoperacyjności. Jednym z nich jest FIPA (FIPA, 1997).

Narzędzie programistyczne JADE

JADE (Java Agent Development Framework) to framework programistyczny w całości zaimplementowany w języku Java, który upraszcza implementację systemów MA poprzez wykorzystanie oprogramowania pośredniczącego spełniającego specyfikacje FIPA (FIPA, 1997). Platforma agentów może być dystrybuowanamiędzy maszynami (które niekoniecznie korzystają z tego samego systemu operacyjnego), a konfiguracją można zarządzać za pomocą zdalnego interfejsu graficznego (GUI) . Architektura komunikacji oferuje elastyczne i wydajne przesyłanie komunikatów, gdzie JADE tworzy i zarządza przychodzącą prywatną kolejką komunikatów ACL dla każdego agenta. Zaimplementowano kompletny model komunikacji FIPA, a jego komponenty zostały wyraźnie rozróżnione. JADE w pełni integruje protokoły interakcji, ACL, ontologie, protokoły transportowe itp. Większość protokołów zdefiniowanych przez FIPA jest dostępna w JADE.

DEFINICJA SYSTEMU WFMS OPARTEGO NA AGENCIE MOBILNYM

Niniejsza praca przedstawia metodologię rozwoju systemu WFMS opartego na agencie mobilnym. Podstawową ideą takiego systemu jest to, że MA kieruje procesem przepływu pracy przez różne jednostki organizacyjne, w których wykonywane są różne zadania zgodnie z rozpatrywanym przypadkiem. W fazie projektowania komponenty są opisywane w przejrzysty i zwięzły sposób. System jest opisywany jako zbiór połączonych ze sobą jednostek organizacyjnych, które mają określoną alokację zasobów. Zachowanie agenta jest określane przez dwa rodzaje specyfikacji:

a) opis ogólnego zachowania agenta i wspólnej wiedzy dla wszystkich agentów, a mianowicie podstawowych operacji i protokołów interakcji (współpraca i rywalizacja o zasoby); oraz b) szczegółowe opisy konkretnego zachowania, takie jak plan zadań i mapa drogowa dostępności, które odpowiednio opisują przypisany proces i dozwolony dostęp do jednostek organizacyjnych.

Faza wdrażania jest wspierana przez wytyczne dotyczące tworzenia oprogramowania, umożliwiające definiowanie komponentów Java (z wykorzystaniem również oprogramowania pośredniczącego JADE) na podstawie specyfikacji systemów agentowych z fazy projektowania. Uzyskane oprogramowanie jest dystrybuowane w zestawie komputerów połączonych w sieć, które zarządzają migracją MA. Modułowość pozwala na bezproblemową adaptację do zmian specyfikacji systemu. Dla ułatwienia czytelności proponowaną metodę zilustrowano studium przypadku dotyczącym procesów likwidacyjnych w firmie ubezpieczeniowej.

Opis studium przypadku

Problem można zdefiniować następująco: "Zdefiniuj WF dla procesów rozpatrywania roszczeń w firmie ubezpieczeniowej, w której klient zgłasza roszczenie z polisy ubezpieczeniowej obejmującej majątek osobisty (nieruchomości, samochód, ubezpieczenie na życie). Firma musi przyjąć roszczenie, zażądać od klienta danych osobowych (numer polisy ubezpieczeniowej itp.) oraz zweryfikować ważność ubezpieczenia, wypłaty i beneficjentów. Musi dokonać korekty szkód rzeczywistych, zweryfikować sprawę, obliczyć wycenę korespondencyjną, dokonać niezbędnych wypłat na rzecz klienta, jeśli reklamacja jest uzasadniona, lub poinformować o tym w przypadku, gdy proces zawiera nieprawidłowe dane".

Metodologia projektowania

Administrator zarządzający procesem w firmie musi posiadać wcześniejszą wiedzę na temat alokacji jednostek organizacyjnych, alokacji zasobów, planu realizacji, listy zadań do wykonania oraz różnych niezbędnych protokołów dotyczących pozyskiwania zasobów lub konkursu. Dodatkowo administrator zarządzający musi znać strukturę środowiska, która jest najpierw określana. Specyfikacja środowiska. Środowisko agenta jest definiowane za pomocą diagramu, który przedstawia ogólną strukturę firmy. Konieczne jest zidentyfikowanie różnych działów, w których wykonywane jest dane zadanie lub przepływa informacja, biorąc pod uwagę wszystkie możliwe przypadki. Następnie każdy dział lub biuro jest reprezentowane przez kontener agenta JADE, co pozwala nam założyć, że każdy kontener znajduje się na innym hoście rozproszonego systemu sieciowego. W ten sposób każdy dział jest reprezentowany przez hosta. Host może należeć do różnych platform, ale dla uproszczenia zakładamy, że wszystkie hosty należą do tej samej platformy. Poniżej proponujemy strategię definiowania platformy, ale może ona mieć inny rozkład. Zatem, w przypadku rozkładu platformy ważne jest, aby:

o Zidentyfikować działy zaangażowane w proces, biorąc pod uwagę wszystkie możliwe przypadki.
o Określ przepływ informacji i jego kierunek.
o Stwórz diagram blokowy na podstawie uzyskanych informacji.

Na tym diagramie każdy blok reprezentuje lokalizację lub hosta systemu rozproszonego (każdy host ma kontener agenta JADE), a strzałki reprezentują kierunek przepływu lub możliwą migrację agenta. Załóżmy, że w naszym przypadku istnieje pięć działów: recepcja, walidacja, ocena, regulacja i płatność; diagram blokowy i możliwe konfiguracje platformy można zobaczyć na rysunku 2. W JADE tworzenie kontenerów odbywa się w następujący sposób:

o Kontener główny. W wierszu poleceń witryny, która ma mieć ten konkretny rodzaj kontenera, możemy napisać: C:\ java JADE.Boot -container-name Nazwa_Host[-gui], gdzie każdy [] reprezentuje opcjonalny parametr.
o Pozostałe kontenery tworzy się za pomocą wiersza:

C:\ java JADE.Boot -container-name Name_Host - container -host HostMainContainer

o Do tworzenia kontenerów i agentów można również użyć graficznego interfejsu użytkownika JADE.

Definicja agenta mobilnego. W studium przypadku stany ogólnego zachowania agenta można łatwo przedstawić dla sieci Petriego . Agent mobilny (MA) wybiera wykonanie planu zgodnie z definicją procesu WF dla przypisanego przypadku; plan wskazuje, które lokalizacje agent musi odwiedzić, aby przetworzyć przypadek, mapę dostępu do lokalizacji, informacje o rezerwacji zasobów. Agent migruje również z jednej lokalizacji do drugiej, współpracuje z innymi agentami, konkuruje o alokację zasobów itd. W JADE agent mobilny jest tworzony jako podklasa klasy ogólnej Agent, a jego usługa jest rejestrowana w DF JADE. Możemy użyć kodu z Załącznika A. Konkretne zachowanie tego agenta jest podane dla definicji procesu WF. Innymi słowy, jest zdefiniowane dla kolejności wykonywania zadań zaangażowanych w proces danego przypadku. Do programowania planu możemy wykorzystać dostępne zachowania JADE, ponieważ reprezentują one zadania, które agent może wykonać. Możemy użyć dowolnego z różnych zachowań zawartych w JADE, zgodnie z planem wykonania. Plan pochodzi z definicji procesu WF; definiuje on kolejność wykonywania zadań, które są w nim zawarte; dlatego czasami konieczne jest skonstruowanie diagramu (takiego jak diagram przepływu) określającego kolejność, jeśli zawiera ona alternatywy; diagram musi wskazywać, w którym dziale zadanie ma zostać wykonane. Postępując zgodnie ze studium przypadku, załóżmy, że uzyskany diagram jest taki jak na rysunku 4; na rysunku tym wskazana jest zarówno nazwa zadania, jak i odpowiadający mu dział. Jeśli kolejność wykonywania zadań jest zgodna z działaniem skończonej maszyny stanów (FSM), używamy

JADE FSMBehaviour. FSMBehaviour fsm = new FSMBehaviour(this) { public int onEnd() {
System.out.println("Zachowanie FSM zakończone");
myAgent.doDelete();
return super.onEnd();} };

Jeśli używamy tego konkretnego zachowania, musimy zarejestrować odpowiednie stany, które reprezentują każde zadanie do wykonania, oraz przejścia, które reprezentują jego sekwencję lub kolejność wykonywania. W ten sposób do rejestru stanów używana jest funkcja:

registerState(Function_Name_Taski, state_namei),

gdzie pierwszy parametr wskazuje nazwę funkcji dla odpowiedniego zadania, a drugi parametr wskazuje nazwę tego stanu używaną do rejestracji przejść. W tym celu używamy funkcji:

RegisterDefaultTransition(state_name1, state_name2),

która wskazuje, że po całkowitym wykonaniu funkcji reprezentowanej dla stanu state_name1, wykonywana jest funkcja dla stanu state_name2. Niektóre stany i przejścia w studium przypadku mogłyby być pokazane na rysunku 4. Należy również dodać inne stany (MovValBehaviour, MovValoBehaviour, MovCotizBehaviour i MovPayBehaviour) w celu migracji agenta, gdy wykonywane zadanie musi zostać zrealizowane w innym dziale niż obecny. Ze względu na migrację agenta, odpowiednia ontologia mobilności musi zostać zarejestrowana:

getContentManager().registerLanguage(new SLCodec(), FIPAN-
names.ContentLanguage.FIPA_SL0);
// zarejestruj ontologię mobilności
getContentManager().registerOntology(MobilityOntology.get-
Instance());

Po zarejestrowaniu stanów dla FSMBehaviour używamy jedynie nazwy funkcji do wykonania; dlatego konieczne jest dodanie instrukcji Java dla każdej funkcji dla wybranego zachowania. Każda z tych metod jest dodawana jako klasa dziedzicząca po jednym z zachowań JADE. Metody te zawierają instrukcje do wykonania w każdym zadaniu. Jeśli agent musi współpracować z innym agentem w celu wykonania zadania, można użyć protokołu JADE FIPA-Request . Postępując zgodnie z powyższymi wytycznymi, można zdefiniować ogólnezachowanie MA i środowiska, w którym się rozwija. W podobny sposób można również określić zachowanie agentów stacjonarnych. Proponowana metodologia została zastosowana w kilku studiach przypadków prowadzących do modułowego oprogramowania, które zostało uruchomione na kilku komputerach osobistych w sieci LAN. Testy przeprowadzono w lokalizacjach, w których zdefiniowano platformę JADE. Niemniej jednak, w systemie WFMS można zintegrować różne platformy konfiguracyjne.

PRZYSZŁE TRENDY

Proponowana metodologia rozwoju WFMS stanowi pierwszy krok w kierunku automatyzacji złożonych procesów biznesowych w dużych przedsiębiorstwach. Jednak w firmach, w których jednostki organizacyjne są rozproszone w kilku miastach, MA musi być zintegrowane z siecią;wtedy konieczne jest dodanie bardziej zaawansowanych funkcji do agentów i ich środowiska, a mianowicie protokołów bezpieczeństwa i kontroli strat agentów. Ponadto korzystne byłoby rozważenie interakcji z istniejącymi systemami WFMS w oparciu o standardy WFMC, aby wykorzystać istniejące informacje i strategie biznesowe.

WNIOSKI

Automatyzacja procesów biznesowych przyczynia się do poprawy produktywności firm. W niniejszej pracy zaproponowano metodologię rozwoju WFMS w oparciu o technologię agentów mobilnych. Metodologia ta pozwala na modułowe definiowanie środowiska i zachowań agentów mobilnych. Proponowana technika implementacji wykorzystuje JADE, wykorzystując wszystkie zalety JAVA. Agent mobilny może wchodzić w interakcje z innymi agentami, współpracując, negocjując lub konkurując o zasoby. Dzięki modułowości uzyskanego oprogramowania można je łatwo modyfikować zgodnie ze specyfikacjami WFMS.