WSTĘP

Wraz z rosnącym zapotrzebowaniem na wyszukiwanie informacji multimedialnych, takich jak pobieranie obrazów i wideo z Internetu, istnieje potrzeba znalezienia sposobów uczenia klasyfikatora, gdy zbiór danych szkoleniowych jest połączony z małą liczbą danych oznaczonych etykietą i dużą liczbą danych nieoznaczonych . Tradycyjne metody uczenia się z nadzorem i bez nadzoru nie nadają się do rozwiązywania takich problemów, szczególnie gdy problem jest związany z danymi w przestrzeni o dużych wymiarach. W ostatnich latach zaproponowano wiele metod, które można ogólnie podzielić na dwie grupy: uczenie się częściowo nadzorowane i uczenie się aktywne (AL). Maszyna wektorów nośnych (SVM) została uznana za skuteczne narzędzie do rozwiązywania problemów wielowymiarowych. Od przełomu wieków wielu badaczy zaproponowało algorytmy aktywnego uczenia się z SVM (ALSVM). Biorąc pod uwagę ich szybki rozwój, w tym rozdziale dokonamy przeglądu najnowocześniejszego rozwiązania ALSVM w rozwiązywaniu problemów klasyfikacyjnych.

TŁO

Ogólne ramy AL można opisać tak.

Krok inicjalizacji: Klasyfikator h jest szkolony na początkowym oznaczonym zbiorze treningowym L

krok 1: Uczeń ocenia każde dane x w potencjalnym zestawie zapytań Q (podzbiór lub cały nieoznakowany zbiór danych U) i wysyła zapytanie do próbki x*, która ma najniższą wartość EvalFun(x, L, h, H) do wyroczni i otrzymuje jej etykietę y*;
krok 2: Uczeń aktualizuje klasyfikator h powiększonym zbiorem uczącym {L + ( x*, y*)};
krok 3: Powtarzaj kroki 1 i 2 aż do zakończenia treningu;

Gdzie

•  EvalFun(x, L, h, H): funkcja oceny potencjalnego zapytania x (najlepsza jest tu najniższa wartość)
•  L: bieżący oznaczony zestaw treningowy
•  H: przestrzeń hipotez

Widać wyraźnie, że jego nazwa - aktywne uczenie się - bierze się z faktu, że uczący się może doskonalić klasyfikator poprzez aktywne wybieranie "optymalnych" danych z potencjalnego zbioru zapytań Q i dodanie go do bieżącego oznaczonego zestawu treningowego L po otrzymaniu jego etykiety podczas procesów. Kluczowym punktem AL są kryteria doboru próby. W przeszłości AL był używany głównie w połączeniu z algorytmem sieci neuronowej i innymi algorytmami uczenia się. Statystyczna AL jest jedną z klasycznych metod, w której próbka minimalizująca wariancję, obciążenie lub błąd uogólnienia jest kierowana do wyroczni. Chociaż metody te mają mocne podstawy teoretyczne, istnieją dwa typowe problemy ograniczające ich zastosowanie: jeden dotyczy sposobu szacowania późniejszego rozkładu próbek, a drugi to zbyt wysoki koszt obliczeń. Aby uporać się z powyższymi dwoma problemami, opracowano szereg metod AL opartych na przestrzeni wersji, które opierają się na założeniu, że funkcję celu można doskonale wyrazić za pomocą jednej hipotezy w przestrzeni wersji i w której próbka może zmniejszyć objętość zaproponowano przestrzeń wersji. Przykładami są zapytania komisji oraz SG AL . Jednak złożoność przestrzeni wersji sprawiła, że były one trudne do rozwiązania, dopóki nie pojawiły się maszyny ALSVM oparte na przestrzeni wersji. Sukces SVM w latach 90. skłonił badaczy do połączenia AL z SVM, aby uporać się z problemami uczenia się z półnadzorem, takimi jak nauczanie na odległość , RETIN oraz wielowidoczność oparte na maszynach ALSVM. W poniższych sekcjach podsumowujemy istniejące dobrze znane maszyny ALSVM w ramach teorii przestrzeni wersji, a następnie krótko opisujemy niektóre strategie mieszane. Na koniec omówimy trendy badawcze dotyczące ALSVM i przedstawimy wnioski .

WERSJA AKTYWNA NAUKA OPARTA NA PRZESTRZENI Z SVM

Ideą prawie wszystkich istniejących heurystycznych maszyn ALSVM jest jawnie lub pośrednio znalezienie próbki, która może zmniejszyć objętość przestrzeni wersji. W tej sekcji najpierw przedstawimy ich podstawy teoretyczne, a następnie dokonamy przeglądu niektórych typowych maszyn ALSVM.

Wersja teorii przestrzeni

W oparciu o prawidłowy model uczenia się z przybliżeniem prawdopodobieństwa celem uczenia maszynowego jest znalezienie spójnego klasyfikatora, który ma najniższy błąd uogólnienia. Granicę błędu uogólnienia Gibbsa definiuje się jako



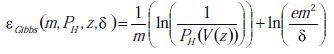
gdzie P_H oznacza rozkład aprioryczny w przestrzeni hipotez H, V(z) oznacza przestrzeń wersji zbioru treningowego z, m jest liczbą z, a δ jest stałą w [0, 1]. Wynika z tego, że błąd uogólnienia związany ze spójnymi klasyfikatorami jest kontrolowany przez objętość przestrzeni wersji, jeśli rozkład przestrzeni wersji jest równomierny. Zapewnia to teoretyczne uzasadnienie dla maszyn ALSVM opartych na przestrzeni wersji.

Zapytanie złożone przez komisję z SVM

Algorytm ten został zaproponowany, w którym losowo wybrano 2 tys. klasyfikatorów, a próba, w przypadku której te klasyfikatory wykazują maksymalną niezgodność, może w przybliżeniu zmniejszyć o połowę przestrzeń wersji, a następnie zostanie zapytana do Wyroczni. Jednakże złożoność struktury przestrzeni wersji prowadzi do trudności w losowym próbkowaniu w jej obrębie. Z powodzeniem zastosowano algorytm gry w bilard do losowego próbkowania klasyfikatorów w przestrzeni wersji SVM, a eksperymenty wykazały, że jego wydajność była porównywalna z wydajnością standardowego ALSVM opartego na odległości ( SD-ALSVM), który zostanie wprowadzony później. Wadą jest to, że procesy są czasochłonne. Standardowe aktywne nauczanie na odległość z SVM W przypadku SVM przestrzeń wersji można zdefiniować jako:



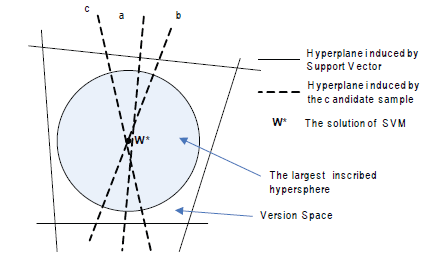
gdzie Φ(.) oznacza funkcję odwzorowującą pierwotną przestrzeń wejściową X na przestrzeń wielowymiarową Φ(X) , a W oznacza przestrzeń parametrów. SVM ma dwie właściwości, które prowadzą do jego podatności na AL. Pierwszą jest jego dwoistość, że każdy punkt w V odpowiada jednej hiperpłaszczyźnie w Φ(X ), która dzieli Φ(X ) na dwie części i odwrotnie. Inną właściwością jest to, że rozwiązanie SVM w* znajduje się w środku przestrzeni wersji, gdy przestrzeń wersji jest symetryczna, lub blisko jej środka, gdy jest asymetryczna. Na podstawie powyższych dwóch właściwości wywnioskowali lemat, że próbka najbliższa granicy decyzyjnej może spowodować, że oczekiwany rozmiar przestrzeni wersji zmniejszy się najszybciej. Zatem próbka najbliższa granicy decyzyjnej zostanie zapytana do wyroczni .

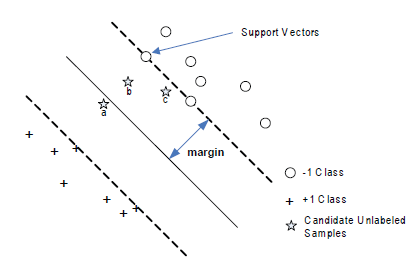
Jest to tak zwana SD-ALSVM, która charakteryzuje się niewielką liczbą dodatkowych obliczeń w celu wybrania badanej próbki i zapewnia doskonałe działanie w rzeczywistych zastosowaniach

Aktywne uczenie się na odległość w trybie wsadowym z SVM

Stosując zapytania wsadowe po prostu wybierano wiele próbek znajdujących się najbliżej granicy decyzyjnej. Jednak dodanie partii takich próbek nie może zapewnić największego zmniejszenia rozmiaru przestrzeni wersji. Chociaż każda próbka może prawie o połowę zmniejszyć przestrzeń wersji, trzy próbki razem mogą nadal zmniejszyć o około 1/2, zamiast 7/8 rozmiaru przestrzeni wersji. Można zaobserwować, że przypisano to małym kątom pomiędzy ich indukowanymi hiperpłaszczyznami. Aby przezwyciężyć ten problem zaproponował nową strategię selekcji poprzez włączenie miary różnorodności, która uwzględnia kąty pomiędzy indukowanymi hiperpłaszczyznami. Niech w bieżącej rundzie oznaczonym zbiorem będzie L, a zbiorem zapytań o pulę Q, następnie w oparciu o kryterium różnorodności należy dodać kolejną próbkę x_q



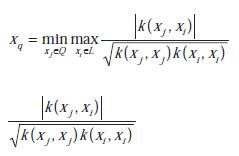
gdzie oznacza wartość cosinus kąta między dwiema hiperpłaszczyznami indukowanymi przez x_j i x_i, dlatego jest znane jako kryterium zróżnicowania kąta. Można zaobserwować, że zmniejszona objętość przestrzeni wersji na tym rysunku



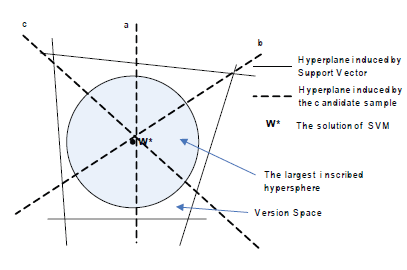
jest większa niż na rysunku tym



Aktywne uczenie się RETIN

Niech [1... ] ( ) j j n I ∈ będą próbkami w potencjalnym zbiorze zapytań Q, a r(i, k) będzie funkcją, która w iteracji i koduje pozycję k w rankingu istotności ze względu na odległość do bieżącej granicy decyzyjnej, wówczas sekwencję można uzyskać w następujący sposób



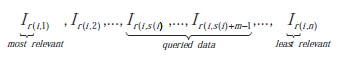
W SD-ALSVM s(i) jest takie jak I_r(i,s(i),…,I_{r(i,s((i)+m-1} to m próbek najbliższych granicy SVM. Strategia ta domyślnie opiera się na silnym założeniu: dokładne oszacowanie granicy SVM. Jednakże granica decyzyjna jest zwykle niestabilna w początkowych iteracjach.(Gosselin i Cord, 2004) zauważyli, że nawet jeśli granica decyzyjna może się znacznie zmieniać podczas wcześniejszych iteracji, funkcja rankingu r() jest dość stabilne. W związku z tym zaproponowali zrównoważone kryterium wyboru, niezależne od granicy i w którym zaprojektowano metodę adaptacyjną do dostrajania s podczas iteracji ze sprzężeniem zwrotnym. Wyrażano je wzorem

s(i+1) = s(i) +h(r_rel(i), r_irr(i)

gdzie h(x, y) = k × (x - y) co charakteryzuje dynamikę układu (k jest stałą dodatnią), r_rel(i) i r_irr(l) oznaczają liczba odpowiednich i nieistotnych próbek w badanym zbiorze w i-tej iteracji. W ten sposób liczba odpowiednich i nieistotnych próbek w badanym zbiorze będzie w przybliżeniu równa.

Kryterium średniej przestrzeni wersji

Zaproponowano kryterium wyboru poprzez minimalizację średniej przestrzeni wersji, która jest zdefiniowana jako



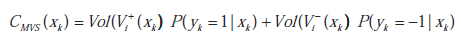
gdzie oznacza objętość przestrzeni wersji po dodaniu nieoznakowanej próbki x_k do zbioru treningowy i-tej rundy. Średnia przestrzeń wersji obejmuje zarówno objętość przestrzeni wersji, jak i prawdopodobieństwa późniejsze. Uznali zatem, że kryterium jest lepsze niż SD-ALSVM. Jednak obliczenia tą metodą są czasochłonne.

Aktywne uczenie się oparte na wielu widokach

W odróżnieniu od algorytmów opartych tylko na jednym całym zestawie funkcji, metody wielu widoków opierają się na wielu podfunkcjach. Najpierw szkoli się kilka klasyfikatorów na różnych zestawach podcech. Następnie próbki, w przypadku których klasyfikatory wykazują największe rozbieżności, tworzą zbiór rywalizacji, z którego wybierane są badane próbki. Najpierw zastosowano w AL, a potem zaimplementowano go za pomocą ALSVM, aby wygenerować algorytm Co-SVM, który, jak stwierdzono, ma lepszą wydajność niż SD-ALSVM. Wiele klasyfikatorów może znaleźć rzadkie próbki, ponieważ obserwują próbki z różnych perspektyw. Taka właściwość jest bardzo przydatna do wyszukiwania różnych części należących do tej samej kategorii. Jednakże metody oparte na wielu widokach wymagają, aby odpowiedni klasyfikator mógł dobrze sklasyfikować próbki i aby wszystkie zestawy cech były nieskorelowane. Trudno jest zapewnić taki stan w rzeczywistych zastosowaniach.

MIESZANE AKTYWNE NAUCZANIE

Zamiast pojedynczych strategii AL w poprzednich sekcjach, w tej sekcji omówimy dwa mieszane tryby AL: jeden łączy różne kryteria selekcji, a drugi włącza uczenie się częściowo nadzorowane do AL.

Hybrydowe aktywne uczenie się

W przeciwieństwie do opracowania nowego algorytmu AL, który działa dobrze we wszystkich sytuacjach, niektórzy badacze argumentowali, że lepszym sposobem jest łączenie różnych metod, które zwykle się uzupełniają, ponieważ każda metoda ma swoje zalety i wady. Intuicyjna struktura strategii hybrydowej to tryb równoległy. Kluczową kwestią jest tutaj ustawienie wag dla różnych metod AL. Najprostszym sposobem jest ustawienie stałych wag zgodnie z doświadczeniem i było to stosowane w większości istniejących metod. Strategie najbardziej istotne/nieistotne mogą pomóc w ustabilizowaniu granicy decyzyjnej, ale charakteryzują się niskim współczynnikiem uczenia się; podczas gdy standardowe metody oparte na odległości charakteryzują się wysokim współczynnikiem uczenia się, ale mają niestabilne granice na początkowych sprzężeniach zwrotnych. Biorąc to pod uwagę połączono te dwie strategie, aby osiągnąć lepszą wydajność niż stosowanie tylko jednej strategii. Jak stwierdzono wcześniej, strategie oparte na różnorodności i odległości również się uzupełniają, a łączą różnorodność kąta, iloczynu wewnętrznego i entropii strategię odpowiednio ze standardową strategią opartą na odległości. Jednak strategia stałych wag nie może dobrze pasować do wszystkich zbiorów danych i wszystkich iteracji uczenia się. Dlatego wagi należy ustawiać dynamicznie. Wszystkie wagi zostały zainicjowane tą samą wartością i zmodyfikowane w późniejszych iteracjach przy użyciu algorytmu EXP4. W ten sposób empirycznie wykazano, że powstały algorytm AL działa prawie równie dobrze, a czasami przewyższa najlepszy algorytm w zespole.

Aktywne uczenie się częściowo nadzorowane

1. Aktywne uczenie się z transdukcyjnym SVM .Na pierwszych etapach SD-ALSVM kilka oznaczonych danych może prowadzić do dużych odchyleń bieżącego rozwiązania od rozwiązania prawdziwego; natomiast jeśli weźmie się pod uwagę próbki nieoznakowane, rozwiązanie może być bliższe prawdziwemu rozwiązaniu. Pokazano, że im obecne rozwiązanie jest bliższe prawdziwemu, tym większy będzie rozmiar przestrzeni wersji. Włączono transdukcyjny SVM (TSVM), aby opracować dokładniejsze rozwiązania pośrednie. Jednakże w kilku badaniach podważono fakt, że TSVM może nie być tak pomocny w oparciu o nieoznakowane dane w teorii i praktyce. Zastosowano zamiast tego techniki uczenia się częściowo nadzorowanego w oparciu o pola Gaussa i funkcje harmoniczne, a poprawę uznano za znaczącą.

2. Włączanie EM do aktywnego uczenia się .Połączono maksymalizację oczekiwań (EM) ze strategią zadawania pytań przez komisję. Oraz zintegrowany algorytm Multi-view AL z EM aby uzyskać algorytm Co-EMT, który może dobrze działać w sytuacji, gdy widoki są niezgodne i skorelowane.

PRZYSZŁE TRENDY

Jak rozpocząć aktywną naukę

AL można traktować jako problem przeszukiwania funkcji celu w przestrzeni wersji, dlatego ważny jest dobry klasyfikator początkowy. Gdy kategoria obiektywna jest zróżnicowana, ważniejszy staje się klasyfikator początkowy, gdyż zły może skutkować zbieżnością do rozwiązania lokalnego optymalnego, tzn. niektóre części kategorii obiektywnej mogą nie zostać poprawnie objęte klasyfikatorem końcowym. Strategie dwuetapowe , uczenie się długoterminowe oraz strategie przedklastrowe są obiecujące.

Aktywne uczenie się oparte na funkcjach

W AL informacje zwrotne od wyroczni mogą również pomóc w zidentyfikowaniu ważnych cech i wykazały, że takie prace mogą znacznie poprawić wydajność końcowego klasyfikatora. Do identyfikacji ważnych cech wykorzystano analizę głównych składowych. Według naszej wiedzy istnieje niewiele raportów poruszających ten problem.

Skalowanie aktywnego uczenia się

Skalowanie AL do bardzo dużej bazy danych nie zostało jeszcze szczegółowo zbadane. Jest to jednak istotna kwestia dla wielu realnych zastosowań. Zaproponowano pewne podejścia do indeksowania bazy danych oraz przezwyciężania złożoności koncepcji w połączeniu ze skalowalnością zbioru danych.

WSTĘP

Poruszane są tematy z tak ważnych obszarów, jak sztuczna inteligencja, geometria obliczeniowa i technologie biometryczne. Główny nacisk położony jest na proponowany paradygmat obliczeń adaptacyjnych i jego zastosowania do modelowania powierzchni i przetwarzania biometrycznego. Dostępność znacznie tańszych urządzeń do przechowywania danych i urządzeń do przechwytywania obrazów o wysokiej rozdzielczości znacząco przyczyniła się w ciągu ostatnich kilku lat do gromadzenia bardzo dużych zbiorów danych (takich jak mapy GIS, próbki biometryczne, filmy itp.). Z drugiej strony stworzyło także istotne wyzwania, których motywacją jest m.in. większe niż kiedykolwiek wolumeny i złożoność danych, których nie da się już rozwiązać poprzez zakup większej ilości pamięci, szybszych procesorów lub optymalizację istniejących algorytmów. Zmiany te uzasadniały potrzebę radykalnie nowych koncepcji przechowywania, przetwarzania i wizualizacji masowych danych. Wychodząc naprzeciw tej potrzebie, przedstawiono oryginalną metodologię opartą na paradygmacie Adaptive Geometric Computing. Metodologia umożliwia przechowywanie złożonych danych w zwartej formie, zapewniając efektywny dostęp do nich, zachowując wysoki poziom szczegółowości oraz wizualizując dynamiczne zmiany w sposób płynny i ciągły. W pierwszej części rozdziału omówiono algorytmy adaptacyjne w wizualizacji w czasie rzeczywistym, w szczególności w zastosowaniach GIS (Systemy Informacji Geograficznej). Pokrótce omówiono struktury danych, takie jak siatka optymalnie adaptacyjna w czasie rzeczywistym (ROAM) i siatka progresywna (PM). Następnie wprowadzono metodę adaptacyjną Adaptive Spatial Memory (ASM), opracowaną przez R. Apu i M. Gavrilovą. Metoda ta umożliwia szybką i wydajną wizualizację złożonych zbiorów danych reprezentujących tereny, krajobrazy oraz cyfrowe modele wysokości (DEM). Pokrótce omówiono jego zalety. W drugiej części rozdziału przedstawiono zastosowanie paradygmatu obliczeń adaptacyjnych i obliczeń ewolucyjnych do symulacji rakiet. W rezultacie wzory można rozwijać i analizować złożone zachowania. Ostatnia część rozdziału łączy koncepcję obliczeń adaptacyjnych i technik opartych na topologii oraz omawia ich zastosowanie w wymagającym obszarze obliczeń biometrycznych.

TŁO

Przez długi czas badacze zadawali pytania dotyczące realistycznego modelowania obiektów ze świata rzeczywistego (takich jak teren, struktura twarzy czy układ cząstek), przy jednoczesnym zachowaniu wydajności renderowania i przestrzeni. Jako rozwiązanie, w ciągu ostatnich dwóch dekad opracowano siatkę, siatkę, TIN, triangulację Delaunaya i inne metody reprezentacji modelu. Większość z nich to metody statyczne, nieodpowiednie do renderowania dynamicznych scen lub zachowywania wyższego poziomu szczegółów. W 1997 roku opracowano pierwsze metody dynamicznej reprezentacji modelu: Real-time Optimally Adapting Mesh (ROAM) oraz Progressive Mesh (PM) . Zaproponowano różne metody redukcji drobnej siatki do zoptymalizowanej reprezentacji, tak aby zoptymalizowana siatka zawierała mniej prymitywów i zapewniała maksymalne szczegóły. Jednakże podejście to miało dwa główne ograniczenia. Po pierwsze, koszt optymalizacji jest bardzo wysoki (kilka minut na optymalizację jednej średniej wielkości siatki). Po drugie, wygenerowana niejednorodna siatka jest nadal statyczna. W rezultacie daje to słabą jakość, gdy obserwuje się tylko niewielką część siatki. Zatem nawet po dalszym udoskonalaniu metody te nie były w stanie poradzić sobie z dużą ilością złożonych danych ani znacznie zróżnicowanym poziomem szczegółowości. Wkrótce zostały one zastąpione innym modelem obliczeniowym renderowania siatek geometrycznych. W modelu zastosowano kryteria ciągłego udoskonalania oparte na metryce błędu, aby optymalnie dostosować się do dokładniejszej reprezentacji. Dlatego też, biorąc pod uwagę reprezentację siatki i niewielką zmianę punktu obserwacji, zoptymalizowaną siatkę dla następnego punktu obserwacji można obliczyć poprzez udoskonalenie istniejącej siatki

Adaptacyjne obliczenia geometryczne

Przedstawiono adaptacyjną technikę wielorozdzielczości do wizualizacji terenu w czasie rzeczywistym, wykorzystującą sprytny sposób dynamicznej optymalizacji siatki w celu uzyskania płynnej i ciągłej wizualizacji z bardzo wysoką wydajnością (liczba klatek na sekundę) . Nasza metoda charakteryzuje się wydajną reprezentacją ogromnego terenu, wykorzystuje efektywne przejście między poziomami szczegółowości i osiąga stałą liczbę klatek na sekundę, zapewniając ciągłość wizualną. U podstaw tej metody leży przetwarzanie adaptacyjne: sformalizowana hierarchiczna reprezentacja, która wykorzystuje zasadę późniejszego udoskonalania. Dzięki temu mamy pełną kontrolę nad złożonością przestrzeni cech. Metryka błędu jest przypisywana w procesie wyższego poziomu, w którym obiekty (lub cechy) są początkowo klasyfikowane do różnych etykiet. Zatem ta metoda adaptacyjna jest bardzo przydatna do reprezentacji przestrzeni cech. W 2006 roku Gavrilova i Apu wykazali, że takie metody mogą działać jako potężne narzędzie nie tylko do renderowania terenu, ale także do planowania ruchu i symulacji adaptacyjnych . Wprowadzili model adaptacyjnej pamięci przestrzennej (ASM), który wykorzystuje podejście adaptacyjne do algorytmu online działającego w czasie rzeczywistym na potrzeby wspólnego planowania ruchu przez wielu agentów. Wykazali, że potężne pojęcie obliczeń adaptacyjnych można zastosować do percepcji i zrozumienia przestrzeni. Stwierdzono, że rozszerzenie tej metody na potrzeby planowania ruchu w 3D w ramach wspólnych badań z grupą prof. I. Kolingerowej jest znacznie skuteczniejsze niż metody konwencjonalne. Najpierw przejdziemy do omówienia obliczeń ewolucyjnych. Demonstrujemy siłę obliczeń adaptacyjnych, opracowując i stosując adaptacyjny model obliczeniowy do symulacji rakiety. Opisane powyżej opracowane algorytmy adaptacyjne mają tę właściwość, że jednostki pamięci przestrzennej mogą tworzyć, udoskonalać i zwijać się, symulując uczenie się, adaptację i reagowanie na bodźce. Rezultatem jest złożony, wieloagentowy algorytm uczenia się, który wyraźnie demonstruje zachowania organiczne, takie jak poczucie terytorium, szlaki, ślady itp. obserwowane w stadach dzikich zwierząt i owadów. Daje to motywację do zbadania mechanizmu mającego zastosowanie do modelowania zachowań roju. Inteligencja roju (SI) jest właściwością systemu, w którym zbiorowe zachowania prostych agentów wchodzących w interakcję lokalnie ze swoim otoczeniem powodują wyłonienie się spójnych, funkcjonalnych, globalnych wzorców. Podstawą jest inteligencja roju do badania zbiorowego (rozproszonego) zachowania grupy agentów bez scentralizowanej kontroli lub zapewnienia modelu globalnego. Agenci w takim systemie mają ograniczoną percepcję (lub inteligencję) i nie są w stanie samodzielnie wykonywać złożonych zadań. Według Bonebeau regulując zachowanie agentów w roju, można wykazać wyłaniające się zachowanie i inteligencję jako zjawisko zbiorowe. Chociaż zjawisko rojenia jest w dużej mierze obserwowane w organizmach biologicznych, takich jak kolonia mrówek czy stado ptaków, ostatnio wykorzystuje się je do symulacji złożonych układów dynamicznych skupionych na osiągnięciu dobrze określonego celu. Przyjrzyjmy się teraz zastosowaniu adaptacyjnego paradygmatu obliczeniowego i koncepcji inteligencji roju do symulacji zachowania rakiety . Przede wszystkim zauważmy, że złożone zachowanie strategiczne można zaobserwować za pomocą zadaniowego sztucznego procesu ewolucyjnego, w którym zachowania poszczególnych rakiet są opisywane z zaskakującą prostotą. Po drugie, globalna skuteczność i zachowanie na rój rakietowy stosunkowo nie ma wpływu zakłócenie lub zniszczenie poszczególnych jednostek. Ze strategicznego punktu widzenia to zachowanie adaptacyjne jest bardzo pożądaną właściwością w zastosowaniach wojskowych, co motywuje nasze zainteresowanie zastosowaniem go do symulacji rakiet. Należy zauważyć, że problem ten został wybrany, ponieważ stanowi złożone wyzwanie, dla którego bardzo trudno jest uzyskać optymalne rozwiązanie przy użyciu tradycyjnych metod. Dynamiczna i konkurencyjna relacja między rakietami i wieżami sprawia, że modelowanie przy użyciu podejścia deterministycznego jest niezwykle trudne. Należy także zaznaczyć, że problem posiada łatwą metrykę ewaluacyjną, pozwalającą na precyzyjne określenie wartości przystosowania. Podsumujmy teraz ideę optymalizacji ewolucyjnej poprzez zastosowanie algorytmu genetycznego do ewolucji genotypu rakiety. Jesteśmy szczególnie zainteresowani obserwacją ewolucji złożonych formacji 3D i strategii taktycznych, których rój uczy się maksymalizować ich skuteczność podczas symulacji ataku. Symulacja opiera się na ataku, uniku i obronie. Podczas gdy rakieta ustala strategię uderzenia w cel, okręt bojowy przygotowuje się do zestrzelenia jak największej liczby rakiet (rysunek 2 ilustruje podstawowe manewry rakiety). Każda próba zniszczenia celu nazywana jest symulacją ataku. Jego skuteczność jest równa liczbie rakiet trafiających w cel. Dlatego wynik symulacji jest łatwo wymierny. Z drugiej strony interakcja między rakietami a pancernikiem jest złożona i nietrywialna. W rezultacie mogą pojawić się strategie wojenne, w których lokalna kara (tj. poświęcenie rakiety) może zoptymalizować globalną skuteczność (tj. strategia oszustwa). Najprostszą formą informacji znaną każdemu pociskowi jest jego położenie i orientacja oraz lokalizacja celu. Informacje te są uzupełniane o informacje o sąsiedztwie i środowisku rakiety, co wpływa na sposób nawigacji rakiety. Do rzeczywistej symulacji zachowania rakiety używamy strategii opartej na zmodyfikowanej wersji techniki flokowania Boidów. Właśnie nakreśliliśmy niezbędny zestaw działań, aby osiągnąć cel lub wejść w interakcję z otoczeniem. Jest to podstawowy element nawigacji rakietowej. Ciąg genów to kolejna ważna część odzwierciedlająca złożoność, z jaką można wybrać takie kierunki działania. Zawiera unikalną kombinację manewrów (takich jak atak, unik itp.), które ewoluują, tworząc złożoną połączoną inteligencję. Opisujemy przydatność genu rakiety pod względem zbiorowej wydajności. Po zbadaniu różnych możliwości opracowaliśmy i wykorzystaliśmy dwuwymiarową funkcję adaptacyjnego przystosowania do ewolucji naprężeń rakietowych w jednym systemie ewolucyjnym.. Po szeroko zakrojonych eksperymentach odkryliśmy wiele interesujących cech, takich jak geometryczna formacja ataku i organiczne zachowania obserwowane wśród rojów, a także bardzo oczekiwane strategie, takie jak równoczesny atak, oszustwo, odwrót i inne strategie. Zbadaliśmy także zdolność adaptacji poprzez losowanie współrzędnych symulacji, odległości, formacji początkowej, szybkości ataku i innych parametrów rakiet oraz zmierzyliśmy średnią i wariancję funkcji przystosowania. Wyniki wykazały, że wiele wyewoluowanych genotypów w dużym stopniu przystosowuje się do środowiska. Właśnie dokonaliśmy przeglądu zastosowania adaptacyjnego paradygmatu obliczeniowego do inteligencji roju i krótko opisaliśmy skuteczną metodę taktycznej symulacji roju. Wyniki wyraźnie pokazują, że rój jest w stanie opracować złożoną strategię w drodze ewolucyjnego procesu mutacji genotypowej. Jak stwierdzono we wstępie, obliczenia adaptacyjne opierają się na paradygmacie o zmiennym poziomie złożoności szczegółowości, w którym zjawisko fizyczne można symulować poprzez ciągły proces lokalnej adaptacji złożoności przestrzennej. Jak zaprezentowała M. Gavrilova w wykładzie plenarnym na konferencji 3IA Eurographics Conference we Francji w 2006 r., paradygmat adaptacyjny jest potężnym modelem obliczeniowym, który można również zastosować w rozległym obszarze badań biometrycznych. Dlatego w tej części dokonano przeglądu metod i technik opartych na adaptacyjnych metodach geometrycznych w zastosowaniu do problemów biometrycznych. Podkreśla korzyści, jakie inteligentne podejście do obliczeń geometrycznych wnosi do obszaru złożonego przetwarzania danych biometrycznych . W technologii informacyjnej biometria odnosi się do badania cech fizycznych i behawioralnych w celu identyfikacji osoby. W ostatnich latach obszar biometrii odnotował ogromny rozwój, częściowo w wyniku pilnej potrzeby zwiększenia bezpieczeństwa, a częściowo w odpowiedzi na nowy postęp technologiczny, który dosłownie zmienia nasz sposób życia. Dostępność znacznie tańszych pamięci masowych i urządzeń do biometrycznego przechwytywania obrazu o wysokiej rozdzielczości przyczyniły się do gromadzenia bardzo dużych zbiorów danych biometrycznych. We wcześniejszych sekcjach badaliśmy tło adaptacyjnego generowania siatki. Przyjrzyjmy się teraz badaniom podstawowym w zakresie struktur danych opartych na topologii i ich zastosowaniu w badaniach biometrycznych. Informacje te są bardzo istotne dla celów modelowania i wizualizacji złożonych danych biometrycznych. W tym samym czasie, gdy rozwijała się metodologia adaptacyjna w GIS, znacznie wzrosło zainteresowanie strukturami danych opartymi na topologii, takimi jak diagramy Woronoja i triangulacje Delaunaya. Zaczęły pojawiać się wstępne wyniki dotyczące wykorzystania tych struktur danych opartych na topologii w biometrii. Niedawno uzyskano kilka interesujących wyników w BTLab na Uniwersytecie Calgary poprzez opracowanie algorytmów ekstrakcji cech w oparciu o topologię do dopasowywania odcisków palców , modelowania wyrazu twarzy 3D oraz syntezę tęczówki . Kompleksowy przegląd podejść opartych na topologii w modelowaniu i syntezie biometrycznej można znaleźć w najnowszym rozdziale książki na ten temat .Proponujemy radzenie sobie z wyzwaniami wynikającymi z dużych ilości złożonych danych biometrycznych poprzez innowacyjne wykorzystanie paradygmatu adaptacyjnego. Sugerujemy połączenie metodologii opartej na topologii i hierarchii do przechowywania i wyszukiwania danych biometrycznych, a także optymalizacji takiej reprezentacji w oparciu o dostęp do danych i wykorzystanie. Mianowicie odzyskiwanie danych, czyli tworzenie wizualizacji w czasie rzeczywistym, może opierać się na dynamicznym wzorcu wykorzystania danych (jak często, jaki rodzaj danych, ile szczegółów itp.), rejestrowanym i analizowanym w procesie systemu biometrycznego wykorzystywane do celów rozpoznania i identyfikacji. Oprócz wykorzystania tych informacji do zoptymalizowanej reprezentacji i wyszukiwania danych, proponujemy również włączenie inteligentnych technik uczenia się w celu przewidywania najbardziej prawdopodobnych wzorców wykorzystania systemu oraz odpowiedniego reprezentowania i organizowania danych. Z praktycznego punktu widzenia, aby osiągnąć nasz cel, proponujemy nowatorski sposób reprezentowania złożonych danych biometrycznych poprzez organizację danych w hierarchiczną strukturę przypominającą drzewo. Taka organizacja jest w zasadzie podobna do pododdziału pamięci adaptacyjnej (AMS), zdolnej do reprezentowania i wyszukiwania różnej ilości informacji i poziomu szczegółowości, które muszą być reprezentowane. Przestrzenne drzewo czworokątne służy do przechowywania informacji o systemie, a także instrukcji dotyczących przetwarzania tych informacji. Rozszerzanie odbywa się poprzez technikę podziału przestrzennego, która udoskonala dane i zwiększa poziom szczegółowości, a zwijanie odbywa się poprzez operację scalania, która upraszcza reprezentację danych i czyni ją bardziej zwartą. Strategia zachłanna służy do optymalnego dostosowania się do najlepszej reprezentacji w oparciu o wymagania użytkownika, ilość dostępnych danych i zasobów, wymaganą rozdzielczość i tak dalej. Ta potężna technika pozwala nam osiągnąć cel, jakim jest zwarta reprezentacja danych biometrycznych, która pozwala na przykład efektywnie przechowywać drobne szczegóły modelowanej twarzy (np. blizny, zmarszczki) czy szczegółowe wzorce tęczówki.

PRZYSZŁE TRENDY

Oprócz reprezentacji danych technika adaptacyjna może być bardzo użyteczna w ekstrakcji cech biometrycznych w celu szybkiego i niezawodnego wyszukiwania i dopasowywania danych biometrycznych oraz we wdrażaniu dynamicznych zmian w modelu. Metodologia ma duży potencjał, aby stać się jednym z kluczowych podejść w modelowaniu i syntezie danych biometrycznych.

WNIOSEK

Dokonano przeglądu adaptacyjnego paradygmatu obliczeniowego w zastosowaniu do modelowania powierzchni, obliczeń ewolucyjnych i badań biometrycznych. Niektóre z kluczowych przyszłych wydarzeń w nadchodzących latach niewątpliwie uwydatnią ten obszar, inspirując nowe generacje inteligentnych systemów biometrycznych z zachowaniem adaptacyjnym.

WSTĘP

Odkąd nadeszła era komputerów, jednym z najważniejszych obszarów technologii informatycznych było "wspomaganie decyzji". Dziś ten obszar jest ważniejszy niż kiedykolwiek. Pracując w dynamicznym i ciągle zmieniającym się środowisku, współcześni menedżerowie są odpowiedzialni za szereg dalekosiężnych decyzji: czy firma powinna zwiększyć czy zmniejszyć liczbę pracowników? Wejść na nowe rynki? Opracowywać nowe produkty? Inwestować w badania i rozwój? I tak dalej. Jednak pomimo nieodłącznej złożoności tych kwestii i stale rosnącego ładunku informacji, z którymi muszą sobie radzić menedżerowie biznesowi, wszystkie te decyzje sprowadzają się do dwóch podstawowych pytań: Co prawdopodobnie wydarzy się w przyszłości? Jaka jest obecnie najlepsza decyzja? Niezależnie od tego, czy zdajemy sobie z tego sprawę, czy nie, te dwa pytania przenikają nasze codzienne życie - zarówno na poziomie osobistym, jak i zawodowym. Jadąc na przykład do pracy, musimy przewidzieć natężenie ruchu, zanim będziemy mogli wybrać najszybszą trasę dojazdu. W pracy musimy przewidzieć popyt na nasz produkt, zanim będziemy mogli zdecydować, ile go wyprodukować. Zanim zainwestujemy na rynku zagranicznym, musimy przewidzieć przyszłe kursy walut i zmienne ekonomiczne. Wydaje się, że niezależnie od podejmowanej decyzji i jej złożoności, najpierw trzeba przewidzieć, co prawdopodobnie wydarzy się w przyszłości, a następnie na tej podstawie podjąć najlepszą decyzję. Ten fundamentalny proces leży u podstaw podstawowych założeń Adaptive Business Intelligence.

TŁO

Mówiąc najprościej, Adaptive Business Intelligence to dyscyplina łącząca przewidywanie, optymalizację i zdolność adaptacji w system będący w stanie odpowiedzieć na te dwa podstawowe pytania: Co prawdopodobnie wydarzy się w przyszłości? i Jaka jest obecnie najlepsza decyzja? . Aby zbudować taki system, musimy najpierw zrozumieć metody i techniki umożliwiające przewidywanie, optymalizację i adaptację (Dhar i Stein, 1997). Na pierwszy rzut oka tematyka ta nie jest niczym nowym, gdyż na temat analityki biznesowej (Vitt i in., 2002; Loshin, 2003), eksploracji danych i metod przewidywania napisano już setki książek i artykułów (Weiss i Indurkhya, 1998; Witten). i Frank, 2005), metody prognozowania (Makridakis i in., 1988), techniki optymalizacji (Deb 2001; Coello i in. 2002; Michalewicz i Fogel, 2004) i tak dalej. Jednak w żadnym z nich nie wyjaśniono, jak połączyć te różne technologie w system oprogramowania, który jest w stanie przewidywać, optymalizować i dostosowywać. Adaptive Business Intelligence rozwiązuje właśnie ten problem. Jest oczywiste, że przyszłość branży analityki biznesowej leży w systemach mogących podejmować decyzje, a nie w narzędziach generujących szczegółowe raporty (Loshin 2003). Większość menedżerów biznesowych zdaje sobie teraz sprawę, że istnieje ogromna różnica między posiadaniem dobrej wiedzy i szczegółowych raportów a podejmowaniem mądrych decyzji. Michael Kahn, reporter technologiczny agencji Reuters w San Francisco, w artykule z 16 stycznia 2006 r. zatytułowanym "Oprogramowanie do analizy biznesowej patrzy w przyszłość" przedstawia słuszną uwagę: "Ale analitycy twierdzą, że aplikacje, które faktycznie odpowiadają na pytania, a nie tylko przedstawiają góry danych, są kluczowy czynnik napędzający rynek, który w 2006 r. ma wzrosnąć o 10 procent, czyli około dwukrotnie szybciej niż ogólnie w przypadku branży oprogramowania biznesowego. "Coraz częściej powstają aplikacje, które skutkują jakimś działaniem" - powiedział Brendan Barnacle, analityk w Pacific Crest Equities. "Obecnie jest to stosunkowo niewielka część, ale wyraźnie widać, gdzie jest przyszłość. To kolejny etap inteligencji biznesowej."

GŁÓWNY TEMAT

"Odpowiedź na mój problem jest ukryta w moich danych… ale nie mogę jej odkopać!" To popularne stwierdzenie krąży od lat, kiedy menedżerowie biznesowi gromadzili i przechowywali ogromne ilości danych w przekonaniu, że zawierają one cenne informacje. Ale menedżerowie biznesowi w końcu odkryLI, że surowe dane rzadko przynoszą jakąkolwiek korzyść, a ich rzeczywista wartość zależy od zdolności organizacji do ich analizy. W związku z tym pojawiło się zapotrzebowanie na systemy oprogramowania zdolne do wyszukiwania, podsumowywania i interpretowania danych dla użytkowników końcowych. Potrzeba ta doprowadziła do powstania setek firm zajmujących się analityką biznesową, które specjalizowały się w dostarczaniu systemów oprogramowania i usług wydobywania wiedzy z surowych danych. Te systemy oprogramowania analizowałyby dane operacyjne firmy i dostarczały wiedzy w postaci tabel, wykresów, wykresów i innych statystyk. Na przykład raport analityki biznesowej może stwierdzać, że 57% klientów to osoby w wieku od 40 do 50 lat lub że produkt X sprzedaje się na Florydzie znacznie lepiej niż w Gruzji.1 W związku z tym ogólnym celem większości systemów analityki biznesowej było: (1) uzyskać dostęp do danych z różnych źródeł; (2) przekształcić te dane w informację, a następnie w wiedzę; oraz (3) zapewnia łatwy w użyciu interfejs graficzny do wyświetlania tej wiedzy. Innymi słowy, system business intelligence miał za zadanie zbierać i trawić dane oraz prezentować wiedzę w przyjazny sposób (zwiększając w ten sposób zdolność użytkownika końcowego do podejmowania trafnych decyzji). Chociaż różne teksty ilustrują związek między danymi a wiedzą na różne sposoby (np. Davenport i Prusak, 2006; Prusak, 1997; Shortliffe i Cimino, 2006), powszechnie akceptowane rozróżnienie między danymi, informacją i wiedzą brzmi: Dane są gromadzone na co dzień w postaci bitów, liczb, symboli i "obiektów". Informacja to "uporządkowane dane", które są wstępnie przetwarzane, oczyszczane, układane w struktury i pozbawione nadmiarowości. Wiedza to "zintegrowana informacja", która obejmuje fakty i relacje, które zostały dostrzeżone, odkryte lub wyuczone. Ponieważ wiedza jest istotnym elementem każdego procesu decyzyjnego (jak mówi stare powiedzenie: "Wiedza to potęga!"), wiele firm postrzega wiedzę jako ostateczny cel. Wygląda jednak na to, że wiedza już nie wystarczy. Firma może "wiedzieć" dużo o swoich klientach - może mieć setki wykresów i wykresów porządkujących klientów według wieku, preferencji, lokalizacji geograficznej i historii sprzedaży - ale kierownictwo może nadal nie być pewne, jaką decyzję podjąć! I tu leży różnica pomiędzy "wspieraniem decyzji" a "podejmowaniem decyzji": cała wiedza świata nie gwarantuje podjęcia właściwej i najlepszej decyzji. Co więcej, ostatnie badania z zakresu psychologii wskazują, że szeroko rozpowszechnione przekonania mogą w rzeczywistości utrudniać proces podejmowania decyzji. Na przykład powszechne przekonania, takie jak "im więcej mamy wiedzy, tym lepsze będą nasze decyzje" lub "potrafimy odróżnić wiedzę użyteczną od nieistotnej", nie są poparte dowodami empirycznymi. Posiadanie większej wiedzy jedynie zwiększa naszą pewność siebie, ale nie poprawia trafności naszych decyzji. Podobnie ludzie zaopatrywani w "dobrą" i "złą" wiedzę często mają problem z rozróżnieniem między nimi, udowadniając, że nieistotna wiedza zmniejsza skuteczność podejmowania decyzji. Obecnie większość menedżerów przedsiębiorstw zdaje sobie sprawę, że istnieje luka między posiadaniem odpowiedniej wiedzy a podejmowaniem właściwych decyzji. Ponieważ luka ta wpływa na zdolność kierownictwa do odpowiedzi na podstawowe pytania biznesowe (takie jak "Co należy zrobić, aby zwiększyć zyski? Zmniejszyć koszty? Lub zwiększyć udział w rynku?"), przyszłość analityki biznesowej leży raczej w systemach, które mogą dostarczać odpowiedzi i rekomendacji. niż Kopce wiedzy w formie raportów. Przyszłość inteligencji biznesowej leży w systemach, które mogą podejmować decyzje! W rezultacie na rynku pojawia się nowy trend o nazwie Adaptive Business Intelligence. Oprócz pełnienia roli tradycyjnego business intelligence (przekształcania danych w wiedzę), Adaptive Business Intelligence obejmuje także proces decyzyjny, który opiera się na przewidywaniu i optymalizacji.Podczas gdy inteligencję biznesową często definiuje się jako "szeroką kategorię programów użytkowych i technologii służących do gromadzenia, przechowywania, analizowania i zapewniania dostępu do danych", termin Adaptive Business Intelligence można zdefiniować jako "dyscyplinę polegającą na wykorzystywaniu technik przewidywania i optymalizacji do budowania samouczące się systemy "decyzyjne"" (jak pokazuje powyższy diagram). Adaptacyjne systemy Business Intelligence obejmują elementy eksploracji danych, modelowania predykcyjnego, prognozowania, optymalizacji i zdolności adaptacyjnych i są wykorzystywane przez menedżerów biznesowych do podejmowania lepszych decyzji. To stosunkowo nowe podejście do analityki biznesowej może zalecić najlepszy sposób działania (na podstawie danych z przeszłości), ale robi to w bardzo szczególny sposób: system Adaptive Business Intelligence zawiera moduły przewidywania i optymalizacji, które rekomendują decyzje niemal optymalne, oraz "moduł adaptacji" umożliwiający ulepszanie przyszłych zaleceń. Takie systemy mogą pomóc menedżerom biznesowym w podejmowaniu decyzji zwiększających wydajność, produktywność i konkurencyjność. Co więcej, nie można przecenić znaczenia zdolności adaptacyjnych. W końcu jaki jest sens używania oprogramowania, które za każdym razem generuje niepełne harmonogramy, niedokładne prognozy popytu i gorsze plany logistyczne? Czy nie byłoby wspaniale zastosować system oprogramowania, który mógłby dostosować się do zmian na rynku? System oprogramowania, który z czasem mógłby być udoskonalany?

PRZYSZŁE TRENDY

Koncepcja adaptowalności z pewnością zyskuje na popularności, i to nie tylko w sektorze oprogramowania. Możliwości adaptacji wprowadzono już we wszystkim, począwszy od automatycznych skrzyń biegów w samochodach (które dostosowują sposób zmiany biegów do stylu jazdy kierowcy), po buty do biegania (dostosowujące poziom amortyzacji do wzrostu i kroku biegacza), aż po wyszukiwarki internetowe (które dostosowują się do ich wyniki wyszukiwania do preferencji użytkownika i wcześniejszej historii wyszukiwania). Produkty te cieszą się dużym zainteresowaniem konsumentów indywidualnych, gdyż pomimo masowej produkcji, po pewnym czasie potrafią dostosować się do preferencji każdego niepowtarzalnego właściciela. Rosnącą popularność zdolności adaptacyjnych podkreśla także niedawna publikacja Departamentu Obrony USA. Zawiera listę 19 ważnych tematów badawczych na następną dekadę, a wiele z nich zawiera termin "adaptacyjny": adaptacyjne skoordynowane sterowanie na dynamicznym polu bitwy wieloagentowym 3D, sterowanie systemami adaptacyjnymi i współpracującymi, interoperacyjność systemów adaptacyjnych, materiały adaptacyjne do pochłaniania energii

Struktury i złożone sieci adaptacyjne do kontroli kooperacyjnej.

Z pewnością już dawno za ważny składnik inteligencji uznano zdolność adaptacji: Alfred Binet (ur. 1857), francuski psycholog i wynalazca pierwszego testu na inteligencję użyteczną, zdefiniował inteligencję jako "...osąd, inaczej zwany zdrowym rozsądkiem, zmysłem praktycznym inicjatywa, zdolność dostosowywania się do okoliczności. Zdolność do adaptacji jest istotnym elementem każdego inteligentnego systemu, ponieważ trudno argumentować, że system jest "inteligentny", jeśli nie ma zdolności do adaptacji. Dla ludzi znaczenie zdolności adaptacyjnych jest oczywiste: nasza zdolność do adaptacji była kluczowym elementem procesu ewolucyjnego. W psychologii zachowanie lub cecha ma charakter adaptacyjny, gdy pomaga jednostce dostosować się i dobrze funkcjonować w zmieniającym się środowisku społecznym. W przypadku sztucznej inteligencji rozważmy szachy program zdolny pokonać światowego mistrza szachowego: Czy powinniśmy nazwać ten program inteligentnym? Prawdopodobnie nie. Wydajność programu możemy przypisać jego zdolności do oceny aktualnej sytuacji na tablicy w porównaniu z wieloma możliwymi "przyszłymi tablicami" przed wybraniem najlepszego ruchu. Ponieważ jednak program nie może nauczyć się nowych zasad ani dostosować do nich, utraci swoją skuteczność, jeśli zasady gry ulegną zmianie lub modyfikacji. W konsekwencji, ponieważ program nie jest w stanie nauczyć się nowych zasad ani przystosować się do nich, nie jest inteligentny. To samo dotyczy każdego systemu ekspertowego. Nikt nie kwestionuje przydatności systemów ekspertowych w niektórych środowiskach (które są zwykle dobrze zdefiniowane i statyczne), ale systemów ekspertowych, które nie są zdolne do uczenia się i adaptacji, nie należy nazywać "inteligentnymi". Zaprogramowano pewną wiedzę ekspercką, to wszystko. Jakie są zatem przyszłe trendy w zakresie Adaptive Business Intelligence? Według słów Jima Goodnighta, dyrektora generalnego SAS Institute (Collins i in. 007): "Do niedawna wywiad biznesowy ograniczał się do podstawowych zapytań i raportowania i tak naprawdę nigdy nie zapewniał tak dużej inteligencji…" Jednak to ma się wkrótce zmienić. Keith Collins, dyrektor ds. technologii w SAS Institute uważa, że: "Pojawia się nowa definicja platformy dla analityki biznesowej, w której BI nie jest już definiowana jako proste zapytanie i raportowanie. […] W ciągu najbliższych pięciu lat zobaczymy także zmianę w zarządzaniu wynikami w stronę tego, co nazywamy predykcyjnym zarządzaniem wydajnością, w którym analityka odgrywa ogromną rolę w przechodzeniu od prostych wskaźników do bardziej skutecznych mierników". Ponadto Jim Davis, wiceprezes ds. marketingu w SAS Institute (Collins i in. 2007) stwierdził:

"W ciągu najbliższych trzech do pięciu lat osiągniemy punkt zwrotny, w którym więcej organizacji będzie korzystać z BI, aby skupić się na optymalizacji procesów i wywieraniu wpływu na wyniki finansowe…"

Wreszcie ważne byłoby uwzględnienie zdolności adaptacyjnych w komponentach przewidywania i optymalizacji przyszłych systemów Adaptive Business Intelligence. Odnotowano kilka niedawnych udanych wdrożeń systemów Adaptive Business Intelligence (np. Michalewicz i in. 2005), które zapewniają codzienne wsparcie decyzyjne dużym korporacjom i skutkują wielomilionowym zwrotem z inwestycji. Istnieją również firmy (np. www.solveitsoftware.com), które specjalizują się w rozwoju narzędzi Adaptive Business Intelligence. Konieczne są jednak dalsze wysiłki badawcze. Na przykład większość badań dotyczy uczenia maszynowego skupiła się na wykorzystaniu danych historycznych do budowy modeli predykcyjnych. Po zbudowaniu i ocenie modelu cel zostaje osiągnięty. Ponieważ jednak nowe dane pojawiają się w regularnych odstępach czasu, budowanie i ocena modelu to dopiero pierwszy krok w adaptacyjnej analizie biznesowej. Ponieważ modele te muszą być regularnie aktualizowane (coś, za co odpowiedzialny jest moduł adaptacji), spodziewamy się większego nacisku na ten proces aktualizacji w badaniach nad uczeniem maszynowym. Również częstotliwość aktualizacji modułu przewidywania, która może wahać się od sekund (np. w systemach handlu walutami w czasie rzeczywistym) do tygodni i miesięcy (np. w systemach wykrywania oszustw) może wymagać różnych technik i metodologii. Ogólnie rzecz biorąc, systemy Adaptive Business Intelligence obejmują między innymi wyniki badań z zakresu teorii sterowania, statystyki, badań operacyjnych, uczenia maszynowego i nowoczesnych metod heurystycznych. Oczekujemy również, że w nowoczesnych technikach optymalizacji nadal będą dokonywane duże postępy. W nadchodzących latach coraz więcej publikacji naukowych będzie publikowanych na temat problemów optymalizacyjnych z ograniczeniami i wieloma celami, oraz na problemach optymalizacyjnych stawianych w środowiskach dynamicznych. Jest to istotne, ponieważ większość rzeczywistych problemów biznesowych jest ograniczona, wielocelowa i osadzona w zmieniającym się czasie środowisku.

WNIOSEK

Nic dziwnego, że podstawowe komponenty Adaptive Business Intelligence pojawiają się już w innych obszarach biznesu. Na przykład metodologia Six Sigma jest doskonałym przykładem dobrze zorganizowanej, opartej na danych metodologii eliminowania defektów, odpadów i problemów z kontrolą jakości w wielu branżach. Należy zauważyć, że powyższa sekwencja jest bardzo zbliżona "w duchu" do części poprzedniego diagramu, ponieważ opisuje (bardziej szczegółowo) pętlę kontroli zdolności adaptacyjnych. Jest oczywiste, że musimy "mierzyć", "analizować" i "udoskonalać", ponieważ działamy w dynamicznym środowisku, więc proces doskonalenia jest ciągły. Instytut SAS proponuje inną metodologię, która jest bardziej zorientowana na działania związane z eksploracją danych. Ich metodologia zaleca sekwencję kroków pokazaną na rysunku 4. Ponownie zauważmy, że powyższa sekwencja jest bardzo zbliżona do innej części naszego diagramu, ponieważ opisuje (bardziej szczegółowo) transformację od danych do wiedzy. Nic więc dziwnego, że przedsiębiorstwa kładą duży nacisk na te obszary, gdyż lepsze decyzje zazwyczaj przekładają się na lepsze wyniki finansowe. Lepsze wyniki finansowe to właśnie to, o co chodzi w Adaptive Business Intelligence. Systemy oparte na Adaptive Business Intelligence mają na celu rozwiązywanie rzeczywistych problemów biznesowych, które mają złożone ograniczenia, są osadzone w zmieniających się w czasie środowiskach, mają kilka (prawdopodobnie sprzecznych) celów i gdzie liczba możliwych rozwiązań jest zbyt duża, aby je wyliczyć. Rozwiązanie tych problemów wymaga systemu zawierającego moduły przewidywania, optymalizacji i dostosowywania.

WSTĘP

Sztuczne sieci neuronowe (ANN) (McCulloch i Pitts, 1943) opracowano jako modele ich biologicznych odpowiedników, których celem było naśladowanie rzeczywistych układów neuronowych oraz naśladowanie strukturalnej organizacji i funkcji ludzkiego mózgu. Ich zastosowania opierały się na możliwości samodzielnego projektowania rozwiązania problemu poprzez uczenie się rozwiązania z danych. Przeprowadzono badanie porównawcze implementacji neuronowych wykorzystujących analizę głównych składowych (PCA) i analizę składowych niezależnych (ICA). Do krytycznej oceny i oceny wiarygodności prognoz danych wykorzystano sztucznie wygenerowane dane, dodatkowo zniekształcone białym szumem w celu wymuszenia losowości. Analiza zarówno w dziedzinie czasu, jak i częstotliwości wykazała wyższość oszacowanych niezależnych składowych (IC) w stosunku do głównych składowych (PC) w wiernym odtworzeniu autentycznych (utajonych) sygnałów źródłowych. Obliczenia neuronowe należą do przetwarzania informacji polegającego na adaptacyjnym, równoległym i rozproszonym (lokalnym) przetwarzaniu sygnałów. W analizie danych częstym zadaniem jest znalezienie odpowiedniej podprzestrzeni danych wielowymiarowych do późniejszego przetwarzania i interpretacji. Transformacje liniowe są często stosowane przy wyborze modelu danych ze względu na ich prostotę obliczeniową i koncepcyjną. Niektóre popularne transformaty liniowe to PCA, analiza czynnikowa (FA), dążenie do projekcji (PP), a ostatnio ICA . Ten ostatni pojawił się jako rozszerzenie nieliniowego PCA i rozwinął się w kontekście ślepej separacji źródła (BSS) w przetwarzaniu sygnałów i tablic. ICA ma także związek z najnowszymi teoriami mózgu wzrokowego, które zakładają, że kolejne etapy przetwarzania prowadzą do stopniowego zmniejszania redundancji reprezentacji. Artykuł ten stanowi przegląd architektur neuromorficznych PCA i ICA oraz powiązanych z nimi implementacji algorytmicznych, coraz częściej wykorzystywanych jako techniki eksploracyjne. Dyskusja toczy się na sztucznie generowanych sygnałach źródłowych sub- i supergaussowskich.

TŁO

W obliczeniach neuronowych metody przekształcania sprowadzają się do uczenia się bez nadzoru, ponieważ reprezentacji uczymy się wyłącznie na podstawie danych bez żadnej zewnętrznej kontroli. Niezależnie od charakteru uczenia się, adaptację neuronową można formalnie potraktować jako problem optymalizacji: funkcja celu opisuje zadanie, jakie ma wykonać sieć, a numeryczna procedura optymalizacji pozwala na dostosowanie parametrów sieci (np. wag połączeń, obciążenia, parametrów wewnętrznych). Proces ten sprowadza się do wyszukiwania lub programowania nieliniowego w dość dużej przestrzeni parametrów. Jednakże wszelka wcześniejsza wiedza dostępna na temat rozwiązania może zostać skutecznie wykorzystana do zawężenia przestrzeni poszukiwań. W uczeniu się nadzorowanym dodatkowa wiedza jest włączana do architektury sieci lub reguł uczenia się (Gold, 1996). Mniej obszerne badania skupiały się na uczeniu się bez nadzoru. Pod tym względem zwykle stosowane metody matematyczne wywodzą się z klasycznej wielowymiarowej optymalizacji nieliniowej z ograniczeniami i opierają się na metodzie mnożników Lagrange′a, technikach kar lub barier oraz klasycznych technikach algebry numerycznej, takich jak deflacja/renormalizacja, Procedura ortogonalizacji Grama-Schmidta, czyli rzutowanie na grupę ortogonalną

Modele PCA i ICA

Matematycznie liniowe stacjonarne modele PCA i ICA można zdefiniować na podstawie wspólnego modelu danych. Załóżmy, że niektóre procesy stochastyczne są reprezentowane przez trzy losowe (kolumnowe) wektory x(t), n(t) ∈ ℝ^N i s (t) ∈? ℝ^M ze średnią zerową i skończoną kowariancją, ze składowymi s(t) ={s₁(t),s₂₁(t) … s_M1(t)} będąc statystycznie niezależnym i co najwyżej jednym Gaussem. Niech A będzie prostokątną stałą macierzą N × M o pełnym rzędzie kolumnowym, zawierającą co najmniej tyle wierszy, ile kolumn ( N ≥ M ), i oznacz przez t indeks próbki (tj. czas lub punkt próbkowania), przyjmując wartości dyskretne t = 1, 2, ..., T. Postulujemy istnienie liniowej zależności pomiędzy tymi zmiennymi jak:



Tutaj s(t), x(t), n(t) i A są odpowiednio źródłami, obserwowanymi danymi, (nieznanym) szumem w danych i (nieznaną) macierzą mieszania, podczas gdy a_i =1,2 ,..., i a i M są kolumnami A. Mieszanie ma być natychmiastowe, więc nie ma opóźnienia czasowego pomiędzy (ukrytą) zmienną źródłową s_i(t) i jest mieszaną w obserwowalną zmienną (danych) x_{j/sub>(t) , gdzie i = 1, 2, ..., M i j = 1, 2, ..., N. Rozważmy, że stochastyczny proces wektorowy {x(t)} ∈ ℝ^N ma średnią E{x(t)}= 0 i macierz kowariancji Cx = {x(t)x(t)^T} . Celem PCA jest aby zidentyfikować strukturę zależności w każdym wymiarze i uzyskać macierz transformacji ortogonalnej W o rozmiarze L×N od ?ℝ^N do ?ℝ^L , L < N , taką, że L-wymiarowy wektor wyjściowy y(t)=W x(t) dostatecznie reprezentuje wewnętrzne cechy danych wejściowych, i gdzie macierz kowariancji Csub>y} z {y (t)} jest macierzą diagonalną D z elementami diagonalnymi ułożonymi w kolejności malejącej, , d_i,j ≥ d_i+1,j+1 . Przywrócenie {x(t)} z {y(t)}, powiedzmy 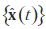, jest w konsekwencji dane wzorem 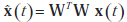. Dla danego L celem PCA jest znalezienie optymalnej wartości W, takiej jak minimalizacja funkcji błędu 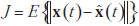. Wiersze w W to PC procesu stochastycznego {x(t)} i wektory własne c_j , 1, 2,...,L wejściowej macierzy kowariancji C_x . Podprzestrzeń rozpięta głównymi wektorami własnymi {c₁,c₂ …c_L} gdzie L < N , nazywana jest podprzestrzenią PCA wymiarowości L. Problem ICA można sformułować następująco: przy danych T realizacjach x(t) , oszacuj zarówno macierz A, jak i odpowiadające jej realizacje s (t). W BSS zadanie jest nieco prostsze i polega na znalezieniu przebiegów {s_i(t} źródeł znających jedynie (obserwowane) mieszaniny {x_j(t)} . Jeśli nie poczyniono żadnych założeń na temat szumu, w (1) pomija się addytywny składnik szumu. Praktyczną strategią jest włączenie szumu do sygnałów jako składnika(ów) uzupełniającego: stąd model ICA przyjmuje postać:

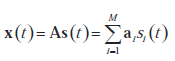Separacja źródeł polega na aktualizacji macierzy rozmieszania B(t), bez odwoływania się do informacji o macierzy mieszania przestrzennego A, tak aby wektor wyjściowy y(t)= B(t) x(t) stał się estymatorem oryginalnych niezależnych sygnałów źródłowych s(t). Macierz rozdzielająca B(t) jest podzielona na dwie części dotyczące zależności w dwóch pierwszych momentach, tj. macierzy wybielającej V(t) oraz zależności w statystyce wyższego rzędu, tj. ortogonalnej macierzy rozdzielającej W(t) w wybielonej przestrzeni. Jeśli założymy, że obserwowane dane x(t) są zerowymi średnimi, to otrzymamy je poprzez wybielanie wektora v(t)= V(t)x(t) dekorelowanymi składnikami. Kolejna transformacja liniowa W(t) szuka rozwiązania poprzez odpowiedni obrót w przestrzeni gęstości składowych i daje y (t )=W(t ) v(t ). Całkowita macierz separacji pomiędzy warstwą wejściową i wyjściową okazuje się być B(t) =W(t) V(t). W standardowym przypadku stacjonarnym wybielanie i ortogonalne macierze separacyjne zbiegają się do pewnych stałych wartości po skończonej liczbie iteracji podczas uczenia, czyli B(t) → B = W V.

IMPLEMENTACJE NEURONALNE

Neuronowe podejście do BSS obejmuje sieć, która ma mieszaniny sygnałów źródłowych na wejściu i generuje przybliżone sygnały źródłowe na wyjściu (rysunek 3). Warunkiem wstępnym jest to, że sygnały wejściowe muszą być wzajemnie nieskorelowane, co jest wymogiem zwykle spełnianym przez PCA. Sygnały wyjściowe muszą jednak być od siebie niezależne, co w naturalny sposób prowadzi z PCA do ICA. Statystyki wyższego rzędu wymagane przez separację źródeł można włączyć do obliczeń bezpośrednio lub poprzez zastosowanie odpowiednich nieliniowości. SSN lepiej pasują do tego drugiego podejścia . Rdzeń dużej klasy neuronowych algorytmów adaptacyjnych składa się z reguły uczenia się i powiązanego z nią kryterium optymalizacji (funkcji celu). Te dwa elementy różnicują algorytmy, które w rzeczywistości są rodzinami algorytmów sparametryzowanych przez zastosowaną funkcję nieliniową. Reguła aktualizacji jest określona przez iteracyjną przyrostową zmianę ΔW macierzy rotacji W, co daje ogólną postać reguły uczenia się:

W → W + ΔW

Neuronowa PCA

Najpierw rozważmy pojedynczy sztuczny neuron otrzymujący M-wymiarowy wektor wejściowy x. Stopniowo dostosowuje swój wektor wag w tak, aby funkcja E{f(w^Tx)} była maksymalizowana, gdzie E jest oczekiwaniem w odniesieniu do (nieznanej) gęstości prawdopodobieństwa x, a f jest ciągłą funkcją celu. Funkcja f jest ograniczona przez ustawienie stałej normy euklidesowej w. Reguła uczenia się z ograniczonym gradientem wznoszenia oparta na sekwencji przykładowych funkcji dla stosunkowo małych szybkości uczenia się α(t) oznacza zatem :

w(t+1)= w(t)+a(t) (I - w(t)Tw(t)) x(t)g(w(t)^Tw(t))

gdzie g = f′ . Wszelkie reguły uczenia się PCA mają tendencję do znajdowania tego kierunku w przestrzeni wejściowej, wzdłuż którego dane mają maksymalną wariancję. Jeśli wszystkie kierunki w przestrzeni wejściowej mają równą wariancję, przypadek jednojednostkowy z odpowiednią nieliniowością w przybliżeniu minimalizuje kurtozę wejścia neuronu. Oznacza to, że wektor wag jednostki będzie wyznaczany przez kierunek w przestrzeni wejściowej, na który rzutowanie danych wejściowych jest w większości skupione i odbiega znacząco od normalności. To zadanie jest zasadniczo celem w technice PP. W przypadku jednowarstwowych sieci ANN składających się z L jednostek równoległych, przy czym każda jednostka i ma ten sam wektor wejściowy M-elementowy x i własny wektor wagowy W_i, które razem tworzą macierz wag M × L W =[w₁ ,w₂,… w_L następująca reguła uczenia uzyskana powyżej jest uogólnieniem liniowej reguły uczenia się PCA (w postaci macierzowej):

W(t+1)= W(t)+a(t) (I - W(t)TW(t)) x(t)g(w(t)^TW(t))

Ze względu na niestabilność powyższego nieliniowej reguły Hebbiana uczenia się dla przypadku wielu jednostek wprowadzono inne podejście polegające na jednoczesnej optymalizacji dwóch kryteriów :

W(t+1)= W(t)+μ(t)(x(t)g(y(t)^T) + γ(t)(I-W(t)W(t)^T))

Tutaj μ(t) jest wybierane jako dodatnie lub ujemne w zależności od tego, czy jesteśmy zainteresowani odpowiednio maksymalizacją lub minimalizacją funkcji celu J₁(w_i = E{f(x^Tw_i)}. Podobnie γ(t) jest kolejnym parametrem wzmocnienia, który jest zawsze dodatni i ogranicza wektory wag do ortonormalności, która jest narzucona przez odpowiednią funkcję kary, taką jak:



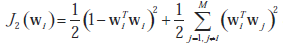
Jest to algorytm bigradientu, który jest iterowany, aż wektory wag osiągną zbieżność z pożądaną dokładnością. Algorytm ten może wykorzystywać znormalizowane uczenie się Hebbiana lub anty-Hebbiana w ujednoliconej formule. Wychodząc od reguły jednej jednostki, wielojednostkowy algorytm bigradientu może jednocześnie wyodrębnić kilka solidnych odpowiedników głównych lub mniejszych wektorów własnych macierzy kowariancji danych . W przypadku wielowarstwowych SSN transfer funkcji ukrytych węzłów można wyrazić radialnymi funkcjami bazowymi (RBF), których parametrów można się nauczyć za pomocą dwustopniowej strategii opadania gradientowego. W celu poprawy wydajności netto stosowana jest nowa, rozwijająca się strategia wstawiania węzłów RBF z różnymi RBF. Podano, że strategia uczenia się oszczędza czas obliczeniowy i przestrzeń pamięci w przybliżeniu mapowań ciągłych i nieciągłych.

Neuronowy ICA

W SSN wdrożono różne formy uczenia się bez nadzoru, wykraczające poza standardowe PCA, takie jak nieliniowe PCA i ICA. Wybielanie danych może być emulowane neuronowo przez PCA za pomocą prostego algorytmu iteracyjnego, który aktualizuje macierz sferyczną V(t):

V(t+1)= V(t)-α(t)(vv^T - I)

Po otrzymaniu macierzy dekorelacji V(t), podstawowym zadaniem algorytmów ICA pozostaje otrzymanie macierzy ortogonalnej W(t ), co jest równoznaczne z odpowiednią rotacją dekorelowanych danych v(t)= V(t)x(t) mające na celu maksymalizację iloczynu gęstości krańcowych jego składników. Istnieją różne podejścia neuronowe do szacowania macierzy rotacji W(t). Ważna klasa algorytmów opiera się na maksymalizacji entropii sieci. Algorytm maksymalizacji informacji nieliniowej BS (infomax) wykonuje online stochastyczne wznoszenie gradientu we wzajemnych informacjach (MI) pomiędzy wyjściami i wejściami sieci. Minimalizując MI pomiędzy wyjściami, sieć rozkłada wejścia na niezależne komponenty. Rozważenie sieci z wektorem wejściowym x(t), macierzą wag W(t) i monotonicznie przekształconym wektorem wyjściowym y=g(Wx+w₀) , to wynikowa reguła uczenia się odpowiednio dla wag i wag błędu systematycznego wynosi:

ΔW= [W^T]^-1 + x(1? 2y)^T a Δw₀ = 1? 2y

W przypadku zmiennych ograniczonych wzajemne oddziaływanie członu antyhebbowskiego x(1?2y)^T i członu przeciwdziałającego rozpadowi [W^T]^-1?? daje gęstość wyjściową bliską płaskiemu rozkładowi stałemu, który odpowiada do maksymalnego rozkładu entropii. Amari, Cichocki i Yang zmienili algorytm BS infomax, wykorzystując gradient naturalny zamiast gradientu stochastycznego, aby zmniejszyć złożoność obliczeń neuronowych i znacząco poprawić szybkość zbieżności. Reguła aktualizacji zaproponowana dla macierzy rozdzielającej to:

ΔW= [I - g(Wx) (Wx)^T]W

Lee rozszerzył zarówno na rozkłady sub-, jak i supergaussowskie, regułę uczenia się opracowaną na podstawie zasady infomax spełniającą ogólne kryterium stabilności i zachowującą prosty początkową architekturę sieci. Stosując do optymalizacji gradient naturalny lub względny , ich zasada uczenia się daje wyniki, które konkurują z obliczeniami wsadowymi o stałym punkcie. Algorytm ekwiwariantnej separacji adaptacyjnej poprzez niezależność (EASI) wprowadzony przez Cardoso i Lahelda (1996) jest nieliniową metodą dekorelacji. Funkcja celu J(W)= E{f(Wx)} poddawana jest minimalizacji przy zastosowaniu ograniczenia ortogonalnego nałożonego na W i nieliniowości g = f′ wybranej według kurtozy danych. Podstawowa zasada aktualizacji jest równa:

ΔW= ?λ (yy^T ? I + g (y)y^T ? yg (y^T ))W

Algorytmy stałoprzecinkowe (FP) przeszukują rozwiązanie ICA poprzez minimalizację wzajemnych informacji (MI) pomiędzy estymowanymi komponentami. Reguła uczenia się FastICA znajduje kierunek w taki, że rzut w^Tx maksymalizuje funkcję kontrastu postaci J_G(w) = [E{f(w^T)} - E{f(v)}]², gdzie v oznacza standaryzowaną zmienną Gaussa. Reguła uczenia się jest w zasadzie metodą dekorelacji podobną do metody Grama-Schmidta.

OCENA ALGORYTMU

Porównawczo uruchamiamy algorytmy neuronowe PCA i ICA, korzystając z syntetycznie wygenerowanych szeregów czasowych, zepsutych addytywnie pewnym białym szumem, aby złagodzić ścisły determinizm . Od tego czasu neuronowa PCA została zaimplementowana przy użyciu algorytmu bigradient działa to zarówno w przypadku minimalizacji, jak i maksymalizacji kryterium J₁ w ramach ograniczeń normalności narzuconych przez funkcję kary J₂. Algorytmy neuronowe ICA obejmowały rozszerzony infomax Bella i Sejnowskiego, póładaptacyjny stałoprzecinkowy szybki algorytm ICA, zaadaptowany wariant algorytmu EASI zoptymalizowany pod kątem danych rzeczywistych oraz rozszerzony uogólniony rozkład lambda (EGLD ) algorytm oparty na maksymalnej wiarygodności. W przypadku źródeł sztucznie generowanych dokładność wyodrębnienia źródeł ukrytych przez algorytm wykonujący ICA można mierzyć za pomocą pewnych wskaźników ilościowych. Pierwszy, którego użyliśmy, został zdefiniowany jako stosunek sygnału do zakłóceń (SIR):



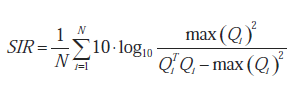
gdzie Q = BA jest ogólną macierzą transformacji ukrytych składników źródła, i Q jest i-tą kolumną Q, max(Q_i) jest maksymalnym elementem Q_i, a N jest liczbą sygnałów źródłowych. Im wyższy jest SIR, tym lepsza jest skuteczność separacji algorytmu. Drugim zastosowanym wskaźnikiem była odległość pomiędzy całkowitą macierzą transformującą Q a idealną macierzą permutacji, którą interpretuje się jako błąd przesłuchu (CTE):



Powyżej Q_ij jest ij-tym elementem Q, max |Q_i|jest maksymalnym elementem wiersza i w Q o maksymalnej wartości bezwzględnej, a max |Q_j| jest elementem kolumny j w Q o maksymalnej wartości bezwzględnej. Macierz permutacji to zdefiniowany tak, że w każdym z jego wierszy i kolumn tylko jeden z elementów jest równy jedności, podczas gdy wszystkie pozostałe elementy są równe zero. Oznacza to, że CTE osiąga minimalną wartość zero dla dokładnej macierzy permutacji (tj. doskonałego rozkładu) i wzrasta dodatnio, im bardziej Q odbiega od macierzy permutacji (tj. rozkładu o mniejszej dokładności). Zdefiniowaliśmy względny błąd wyszukiwania sygnału (SRE) jako odległość euklidesową między sygnałami źródłowymi a ich najlepiej dopasowanymi estymowanymi składowymi, znormalizowaną do liczby sygnałów źródłowych, razy liczbę próbek czasowych, i razy moduł sygnałów źródłowych:



Im niższy jest SRE, tym lepiej szacunki przybliżają ukryte sygnały źródłowe. Stabilizowana wersja algorytmu FastICA jest atrakcyjna ze względu na szybką i niezawodną zbieżność oraz brak parametrów wymagających dostrajania. Naturalny gradient zawarty w rozszerzonym infomaxie BS działa lepiej niż oryginalne wznoszenie gradientowe i jest mniej wymagający obliczeniowo. Chociaż algorytm BS jest teoretycznie optymalny w sensie traktowania wzajemnych informacji jako funkcji celu, podobnie jak wszystkie neuronowe algorytmy bez nadzoru, jego działanie w dużym stopniu zależy od szybkości uczenia się, a jego zbieżność jest raczej powolna. Algorytm EGLD oddziela rozkłady skośne, nawet dla zerowej kurtozy. Pod względem czasu obliczeń najszybszy był rozszerzony algorytm infomax BS, FastICA wierniej pobierał źródła spośród wszystkich testowanych algorytmów, natomiast algorytm EASI wyszedł z macierzą pełnej transformacji Q, która jest najbliższa jedności.

PRZYSZŁE TRENDY

Metody neuromorficzne w analizie eksploracyjnej i eksploracji danych to szybko pojawiające się zastosowania nienadzorowanego treningu neuronowego. W ostatnich latach zaproponowano nowe algorytmy uczenia się, jednak ich właściwości teoretyczne, zakres optymalnego zastosowania i ocena porównawcza pozostają w dużej mierze niezbadane. Z używanymi algorytmami uczącymi nie są powiązane żadne twierdzenia o zbieżności. Co więcej, zbieżność algorytmów w dużym stopniu zależy od właściwego wyboru szybkości uczenia się i nawet po osiągnięciu zbieżności algorytmy neuronowe są stosunkowo powolne w porównaniu z obliczeniami typu wsadowego. Oczekuje się, że nieliniowy i niestacjonarny neuronowy ICA zostanie opracowany dzięki niealgorytmicznemu przetwarzaniu SSN i ich zdolności do uczenia się relacji nieanalitycznych, jeśli zostaną odpowiednio przeszkolone.

WNIOSEK

Zarówno PCA, jak i ICA mają pewne wspólne cechy, takie jak skupienie się na budowaniu modeli generatywnych, które prawdopodobnie wygenerowały zaobserwowane dane, oraz zachowanie informacji i redukcja redundancji. W podejściu neuromorficznym parametry modelu traktowane są jako wagi sieci, które zmieniają się w procesie uczenia. Główna trudność w aproksymacji funkcji wynika z wyboru parametrów sieci, które należy ustalić a priori oraz tych, których należy się nauczyć za pomocą odpowiedniej reguły szkoleniowej. PCA i ICA mają główne zastosowania w eksploracji danych i eksploracyjnej analizie danych, takich jak charakterystyka sygnału, ekstrakcja optymalnych cech i kompresja danych, a także stanowią podstawę klasyfikatorów podprzestrzennych w rozpoznawaniu wzorców. ICA jest znacznie lepiej dopasowana niż PCA do wykonywania BSS, ślepej dekonwolucji i wyrównywania.

WSTĘP

Logika rozmyta stała się podstawą innego podejścia do informatyki. Podczas gdy tradycyjne podejścia do obliczeń były precyzyjne lub miały twarde krawędzie, logika rozmyta umożliwiła zastosowanie mniej precyzyjnego lub bardziej miękkiego podejścia. Podejście, w którym precyzja nie jest najważniejsza, jest nie tylko bliższe sposobowi myślenia człowieka, ale w rzeczywistości może być również łatwiejsze do stworzenia. W ten sposób narodziła się dziedzina miękkiego przetwarzania danych. Do tej dziedziny dodano inne techniki, takie jak sztuczne sieci neuronowe (ANN) i algorytmy genetyczne, oba wzorowane na układach biologicznych. Wkrótce zdano sobie sprawę, że narzędzia te można połączyć i mieszając je ze sobą, mogą zakryć swoje słabe strony, a jednocześnie wygenerować coś, co jest większe niż jego części, czyli krótko mówiąc, tworząc synergię. Adaptacyjny Neuro-fuzzy jest prawdopodobnie najbardziej znaną z tych domieszek miękkich technologii obliczeniowych. Technika ta powstała po zmodyfikowaniu sztucznych sieci neuronowych do pracy z logiką rozmytą, stąd nazwa Neuro-fuzzy . To połączenie zapewnia systemom rozmytym zdolność adaptacji i uczenia się. Później wykazano, że adaptacyjne systemy rozmyte można tworzyć przy użyciu innych technik obliczeń miękkich, takich jak algorytmy genetyczne , zbiory przybliżone i sieci Bayesa , ale powszechnie używana była nazwa Neuro-fuzzy, więc pozostała. Neuro-fuzzy to ogólny opis szerokiej gamy narzędzi i technik używanych do łączenia dowolnego aspektu logiki rozmytej z dowolnym aspektem sztucznych sieci neuronowych. W większości te kombinacje są po prostu rozszerzeniami jednej lub drugiej technologii. Na przykład sieci neuronowe zwykle przyjmują dane wejściowe binarne, ale używają wag o różnej wartości od 0 do 1. Dodawanie zbiorów rozmytych do SSN w celu przekształcenia zakresu wartości wejściowych na wartości, które można wykorzystać jako wagi, jest uważane za rozwiązanie neurorozmyte. Szczególne zainteresowanie zwrócimy na poddziedzinę, w której reguły logiki rozmytej są modyfikowane przez adaptacyjny aspekt systemu. Następna część będzie zorganizowana w następujący sposób: w części 1 przyjrzymy się modelom i technikom używanym do łączenia logiki rozmytej i sieci neuronowych w celu stworzenia systemów neuro-rozmytych. Sekcja 2 zawiera przegląd głównych etapów rozwoju adaptacyjnych systemów neuro-rozmytych. Sekcja 3 kończy się pewnymi zaleceniami i przyszłymi zmianami.

TECHNOLOGIA NEURO-FUZZY

Technologia neuro-fuzzy to szeroki termin używany do opisania dziedziny technik i metod stosowanych do łączenia logiki rozmytej i sieci neuronowych . Logika rozmyta i sieci neuronowe mają swój własny zestaw mocnych i słabych stron, a większość prób połączenia tych dwóch technologii ma na celu wykorzystanie mocnych stron każdej z technik w celu zakrycia słabości pozostałych. Sieci neuronowe mają zdolność samouczenia się, klasyfikacji i kojarzenia danych wejściowych z wynikami. Sieci neuronowe mogą stać się także uniwersalnym aproksymatorem funkcji. Mając wystarczającą ilość informacji o nieznanej funkcji ciągłej, takich jak jej wejścia i wyjścia, sieć neuronową można wytrenować, aby ją aproksymowała. Wadą sieci neuronowych jest to, że nie gwarantują ich zbieżności, czyli prawidłowego wyszkolenia, a po przeszkoleniu nie mogą podać żadnych informacji o tym, dlaczego podejmują określony sposób działania, gdy otrzymają określone dane wejściowe. Logika rozmyta Systemy wnioskowania mogą dostarczyć czytelnych i zrozumiałych dla człowieka informacji o tym, dlaczego podjęto określony sposób działania, ponieważ jest on regulowany przez szereg reguł JEŻELI TO. Systemy logiki rozmytej można dostosować w taki sposób, że ich reguły i parametry zbiorów rozmytych powiązanych z tymi regułami można zmieniać, aby spełnić pewne kryteria. Jednak systemy logiki rozmytej nie mają zdolności do samouczenia się i muszą być modyfikowane przez podmiot zewnętrzny. Inną istotną cechą systemów logiki rozmytej jest to, że podobnie jak sztuczne sieci neuronowe mogą one działać jako uniwersalne aproksymatory. Wspólna cecha możliwości działania jako uniwersalny aproksymator jest podstawą większości prób połączenia tych dwóch technologii. Można go używać nie tylko do aproksymacji funkcji, ale może być również używany zarówno przez sieci neuronowe, jak i systemy logiki rozmytej do wzajemnego aproksymacji. Przybliżenie uniwersalne to zdolność systemu do pewnego stopnia replikowania funkcji. Zarówno sieci neuronowe, jak i systemy logiki rozmytej robią to poprzez wykorzystanie niematematycznego modelu systemu. Używa się terminu przybliżony, ponieważ model nie musi dokładnie odpowiadać symulowanej funkcji, chociaż czasami jest to możliwe, jeśli dostępna jest wystarczająca ilość informacji o funkcji. W większości przypadków doskonała symulacja funkcji nie jest konieczna ani nawet pożądana, ponieważ wymaga czasu i zasobów, które mogą nie być dostępne, a zamknięcie często jest wystarczające.

Kategorie systemów neurorozmytych

Próby połączenia logiki rozmytej i sieci neuronowych trwają od kilku lat i wypróbowano i wdrożono wiele metod. Metody te dzielą się na dwie główne kategorie:

•  Fuzzy Neural Networks (FNN): to sieci neuronowe, które mogą wykorzystywać rozmyte dane, takie jak rozmyte reguły, zbiory i wartości .
•  Systemy rozmyte neuronowe (NFS): to systemy rozmyte "wzmacniane" przez sieci neuronowe .

Istnieją również cztery główne architektury stosowane do wdrażania systemów neuro-rozmytych:

•  Rozmyte sieci wielowarstwowe.
•  Rozmyte sieci samoorganizujących się map
•  Black-Box Fuzzy ANN
•  Architektury hybrydowe.

ROZWÓJ ADAPTACYJNYCH SYSTEMÓW NEURO-ROZMYTYCH

Opracowywanie adaptacyjnego systemu neuro-rozmytego to proces podobny do procedur stosowanych przy tworzeniu systemów logiki rozmytej i sieci neuronowych. Zaletą tego łączonego podejścia jest to, że zwykle nie jest ono bardziej skomplikowane niż każde podejście stosowane indywidualnie. Jak zauważono powyżej, istnieją dwie metody tworzenia systemu neurorozmytego; integrowanie logiki rozmytej ze strukturą sieci neuronowej (FNN) i wdrażanie sieci neuronowych w system logiki rozmytej (NFS). Rozmyta sieć neuronowa to po prostu sieć neuronowa z pewnymi elementami logiki rozmytej; dlatego jest ogólnie szkolony jak normalna sieć neuronowa. Proces szkoleniowy: Schemat szkolenia dla NFS różni się nieco od schematu stosowanego do tworzenia sieci neuronowej i systemu logiki rozmytej pod pewnymi kluczowymi względami, a jednocześnie zawiera wiele ulepszeń w porównaniu z tymi metodami szkoleniowymi. Proces uczenia systemu neurorozmytego składa się z pięciu głównych etapów:

•  Uzyskaj dane szkoleniowe: Dane muszą obejmować wszystkie możliwe wejścia i wyjścia oraz wszystkie krytyczne obszary funkcji, jeśli mają być modelowane w odpowiedni sposób
•  Utwórz system logiki rozmytej: systemem rozmytym może być istniejący system, o którym wiadomo, że działa, na przykład taki, który jest w produkcji od jakiegoś czasu lub taki, który został stworzony zgodnie z metodologią opracowywania systemów eksperckich.
•  Zdefiniuj neuronowe uczenie się rozmyte: Ta faza dotyczy definiowania tego, czego system ma się uczyć. Pozwala to na większą kontrolę nad procesem uczenia się, jednocześnie umożliwiając odkrywanie wiedzy o regułach.
•  Faza treningu: Aby uruchomić algorytm uczenia. Algorytm może posiadać parametry, które można regulować w celu modyfikacji sposobu modyfikacji systemu podczas uczenia.
•  Optymalizacja i weryfikacja: Walidacja może przybierać różne formy, ale zazwyczaj obejmuje dostarczenie do systemu serii znanych danych wejściowych w celu ustalenia, czy system generuje żądany wynik i/lub mieści się w akceptowalnych parametrach. Co więcej, można wyodrębnić reguły i funkcje członkostwa, aby eksperci mogli je sprawdzić pod kątem poprawności

WNIOSKI I PRZYSZŁY ROZWÓJ

Zalety systemów ANF: Chociaż istnieje wiele sposobów wdrożenia systemu Neuro-fuzzy, zalety opisane dla tych systemów są niezwykle jednolite w całej literaturze. Zalety przypisywane systemom neuro-rozmytym w porównaniu z SSN są zwykle związane z następującymi aspektami:

•  Szybsze uczenie: wynika to z ogromnej liczby połączeń występujących w sieci SSN i nietrywialnej liczby obliczeń związanych z każdym z nich. Ponadto większość rozmytych systemów neuronowych można trenować, przeglądając dane raz, podczas gdy sieć neuronowa może wymagać wielokrotnego wystawienia na działanie tych samych danych uczących, zanim osiągną one zbieżność.
•  Mniej zasobów obliczeniowych: Rozmyty system neuronowy jest mniejszy i zawiera mniej połączeń wewnętrznych niż porównywalna sieć SSN, dlatego jest szybszy i zużywa znacznie mniej zasobów.
•  Oferują możliwość wyodrębnienia reguł: Jest to główna zaleta w porównaniu z SSN, ponieważ zasady regulujące system mogą być przekazywane użytkownikom w łatwo zrozumiałej formie.

Ograniczenia systemów ANF: Największe ograniczenie w tworzeniu systemów adaptacyjnych znane jest jako "Klątwa Wymiarowości", której nazwa wzięła się od wykładniczego wzrostu liczby cech, które model musi śledzić w miarę wzrostu liczby atrybutów wejściowych. Każdy atrybut w modelu jest zmienną w systemie, która odpowiada osi na wielowymiarowym wykresie, na którą odwzorowywana jest funkcja. Powiązania pomiędzy różnymi atrybutami odpowiadają liczbie potencjalnych reguł w systemie, określonej wzorem:

N_rules = (L_{linguistic_terms})^variables

Wzór ten staje się bardziej skomplikowany, jeśli istnieje różna liczba zmiennych językowych (zbiorów rozmytych) obejmujących każdy wymiar atrybutu. Na szczęście istnieją sposoby na obejście tego problemu. Ponieważ neuronowy system rozmyty jedynie przybliża modelowaną funkcję, system może nie potrzebować wszystkich atrybutów, aby osiągnąć pożądane wyniki. Inny obszar krytyki w dziedzinie Neuro-fuzzy dotyczy aspektów, których nie można się nauczyć ani przybliżyć. Jednym z najbardziej znanych aspektów jest zastrzeżenie związane z uniwersalnym przybliżeniem. W rzeczywistości aproksymowana funkcja musi być ciągła; funkcja ciągła to funkcja, która nie ma osobliwości, czyli punktu, w którym zmierza do nieskończoności. Inne funkcje, których nauczenie się w adaptacyjnych systemach neuro-rozmytych może sprawiać problemy, to na przykład algorytmy szyfrowania, które zostały celowo zaprojektowane tak, aby były odporne na tego typu analizy.

Przyszły rozwój: Przewidywanie przyszłości zawsze było trudne; jednakże w przypadku technologii ANF przyszły rozwój stał się łatwy ze względu na powszechne wykorzystanie jej technologii bazowej (sieci neuronowe i logika rozmyta). Mieszanie tych technologii tworzy synergię, ponieważ wzajemnie eliminują słabe strony. Technologia ANF umożliwia hodowanie złożonych systemów zamiast konieczności ich budowania przez kogoś. Jednym z najbardziej obiecujących obszarów dla systemów ANF jest wydobywanie systemów. Istnieje wiele przypadków, w których chcemy zautomatyzować system, którego nie można systematycznie opisać w sposób matematyczny. Oznacza to, że nie ma możliwości stworzenia systemu przy użyciu klasycznych metodologii programowania (tj. programowania symulacji). Jeśli mamy odpowiednio duży zbiór przykładów wejść i odpowiadających im wyjść, ANF można wykorzystać do uzyskania modelu systemu. Reguły i powiązane z nimi zbiory rozmyte można następnie wyodrębnić z tego systemu i zbadać pod kątem szczegółów działania systemu. Wiedzę tę można wykorzystać bezpośrednio do zbudowania systemu. Ciekawym zastosowaniem tej technologii jest audyt istniejących złożonych systemów. Wyodrębnione reguły można wykorzystać do określenia, czy reguły odpowiadają wyjątkom od tego, co system powinien robić, a nawet do wykrywania oszustw. Alternatywnie wyodrębniony model może pokazywać alternatywny i/lub bardziej efektywny sposób wdrożenia systemu.

Sztuczne sieci neuronowe (ANN): Sztuczna sieć neuronowa, często nazywana po prostu "siecią neuronową" (NN), to połączona grupa sztucznych neuronów, która wykorzystuje model matematyczny lub model obliczeniowy do przetwarzania informacji w oparciu o koneksjonistyczne podejście do obliczeń. Sieć nabywa wiedzę z otoczenia w procesie uczenia się, a siła połączeń międzyneuronowych (wagi synaptyczne) służy do przechowywania zdobytej wiedzy.

Ewoluująca rozmyta sieć neuronowa (EFuNN): Ewoluująca rozmyta sieć neuronowa to dynamiczna architektura, w której węzły reguł rosną w razie potrzeby i kurczą się w wyniku agregacji. Nowe jednostki reguł i połączenia można łatwo dodawać bez zakłócania istniejących węzłów. Schemat uczenia się często opiera się na koncepcji "węzła zwycięskiej reguły".

Logika rozmyta: Logika rozmyta to obszar zastosowań teorii zbiorów rozmytych, zajmujący się niepewnością w rozumowaniu. Wykorzystuje koncepcje, zasady i metody opracowane w ramach teorii zbiorów rozmytych do formułowania różnych form rozsądnego rozumowania przybliżonego. Logika rozmyta pozwala na ustawienie wartości członkostwa w zakresie (włącznie) od 0 do 1, a w swojej formie językowej pozwala na nieprecyzyjne pojęcia, takie jak "nieznacznie", "całkiem" i "bardzo". W szczególności umożliwia częściowe członkostwo w zestawie.

Rozmyte sieci neuronowe (FNN): to sieci neuronowe wzbogacone o możliwości logiki rozmytej, takie jak wykorzystanie danych rozmytych, reguł, zbiorów i wartości rozmytych. Systemy neurorozmyte (NFS): System neurorozmyty to system rozmyty, który wykorzystuje algorytm uczenia się wywodzący się z teorii sieci neuronowych lub inspirowany nią w celu określenia jego parametrów (zbiorów rozmytych i reguł rozmytych) poprzez przetwarzanie próbek danych.
Mapa samoorganizująca się (SOM): Samoorganizująca się mapa jest podtypem sztucznych sieci neuronowych. Jest szkolony przy użyciu uczenia się bez nadzoru w celu uzyskania niskowymiarowej reprezentacji próbek szkoleniowych, przy jednoczesnym zachowaniu właściwości topologicznych przestrzeni wejściowej. Samoorganizująca się mapa to jednowarstwowa sieć ze sprzężeniem zwrotnym, w której składnie wyjściowe są ułożone w niskowymiarową siatkę (zwykle 2D lub 3D). Każde wejście jest połączone ze wszystkimi neuronami wyjściowymi. Do każdego neuronu dołączony jest wektor wag o tej samej wymiarowości co wektory wejściowe. Liczba wymiarów wejściowych jest zwykle znacznie większa niż wymiar wyjściowy siatki. SOM są używane głównie do redukcji wymiarowości, a nie do rozszerzania.

Soft Computing: Soft Computing odnosi się do partnerstwa technik obliczeniowych w informatyce, sztucznej inteligencji, uczeniu maszynowym i niektórych dyscyplinach inżynieryjnych, które próbują badać, modelować i analizować złożone zjawiska. Głównymi partnerami w tym momencie są logika rozmyta, obliczenia neuronowe, rozumowanie probabilistyczne i algorytmy genetyczne. Zatem zasadą miękkiego przetwarzania danych jest wykorzystanie tolerancji na nieprecyzyjność, niepewność i częściową prawdę w celu osiągnięcia wykonalności, solidności, taniego rozwiązania i lepszego kontaktu z rzeczywistością.

WSTĘP

Sztuczne sieci neuronowe (ANN) (McCulloch i Pitts, 1943) opracowano jako modele ich biologicznych odpowiedników, których celem było naśladowanie rzeczywistych układów neuronowych oraz naśladowanie strukturalnej organizacji i funkcji ludzkiego mózgu. Ich zastosowania opierały się na możliwości samodzielnego projektowania rozwiązania problemu poprzez uczenie się rozwiązania z danych. Przeprowadzono badanie porównawcze implementacji neuronowych wykorzystujących analizę głównych składowych (PCA) i analizę składowych niezależnych (ICA). Do krytycznej oceny i oceny wiarygodności prognoz danych wykorzystano sztucznie wygenerowane dane, dodatkowo zniekształcone białym szumem w celu wymuszenia losowości. Analiza zarówno w dziedzinie czasu, jak i częstotliwości wykazała wyższość oszacowanych niezależnych składowych (IC) w stosunku do głównych składowych (PC) w wiernym odtworzeniu autentycznych (utajonych) sygnałów źródłowych. Obliczenia neuronowe należą do przetwarzania informacji polegającego na adaptacyjnym, równoległym i rozproszonym (lokalnym) przetwarzaniu sygnałów. W analizie danych częstym zadaniem jest znalezienie odpowiedniej podprzestrzeni danych wielowymiarowych do późniejszego przetwarzania i interpretacji. Transformacje liniowe są często stosowane przy wyborze modelu danych ze względu na ich prostotę obliczeniową i koncepcyjną. Niektóre popularne transformaty liniowe to PCA, analiza czynnikowa (FA), dążenie do projekcji (PP), a ostatnio ICA . Ten ostatni pojawił się jako rozszerzenie nieliniowego PCA i rozwinął się w kontekście ślepej separacji źródła (BSS) w przetwarzaniu sygnałów i tablic. ICA ma także związek z najnowszymi teoriami mózgu wzrokowego, które zakładają, że kolejne etapy przetwarzania prowadzą do stopniowego zmniejszania redundancji reprezentacji. Artykuł ten stanowi przegląd architektur neuromorficznych PCA i ICA oraz powiązanych z nimi implementacji algorytmicznych, coraz częściej wykorzystywanych jako techniki eksploracyjne. Dyskusja toczy się na sztucznie generowanych sygnałach źródłowych sub- i supergaussowskich.

TŁO

W obliczeniach neuronowych metody przekształcania sprowadzają się do uczenia się bez nadzoru, ponieważ reprezentacji uczymy się wyłącznie na podstawie danych bez żadnej zewnętrznej kontroli. Niezależnie od charakteru uczenia się, adaptację neuronową można formalnie potraktować jako problem optymalizacji: funkcja celu opisuje zadanie, jakie ma wykonać sieć, a numeryczna procedura optymalizacji pozwala na dostosowanie parametrów sieci (np. wag połączeń, obciążenia, parametrów wewnętrznych). Proces ten sprowadza się do wyszukiwania lub programowania nieliniowego w dość dużej przestrzeni parametrów. Jednakże wszelka wcześniejsza wiedza dostępna na temat rozwiązania może zostać skutecznie wykorzystana do zawężenia przestrzeni poszukiwań. W uczeniu się nadzorowanym dodatkowa wiedza jest włączana do architektury sieci lub reguł uczenia się (Gold, 1996). Mniej obszerne badania skupiały się na uczeniu się bez nadzoru. Pod tym względem zwykle stosowane metody matematyczne wywodzą się z klasycznej wielowymiarowej optymalizacji nieliniowej z ograniczeniami i opierają się na metodzie mnożników Lagrange′a, technikach kar lub barier oraz klasycznych technikach algebry numerycznej, takich jak deflacja/renormalizacja, Procedura ortogonalizacji Grama-Schmidta, czyli rzutowanie na grupę ortogonalną

Modele PCA i ICA

Matematycznie liniowe stacjonarne modele PCA i ICA można zdefiniować na podstawie wspólnego modelu danych. Załóżmy, że niektóre procesy stochastyczne są reprezentowane przez trzy losowe (kolumnowe) wektory x(t), n(t) ∈ ℝ^N i s (t) ∈? ℝ^M ze średnią zerową i skończoną kowariancją, ze składowymi s(t) ={s₁(t),s₂₁(t) … s_M1(t)} będąc statystycznie niezależnym i co najwyżej jednym Gaussem. Niech A będzie prostokątną stałą macierzą N × M o pełnym rzędzie kolumnowym, zawierającą co najmniej tyle wierszy, ile kolumn ( N ≥ M ), i oznacz przez t indeks próbki (tj. czas lub punkt próbkowania), przyjmując wartości dyskretne t = 1, 2, ..., T. Postulujemy istnienie liniowej zależności pomiędzy tymi zmiennymi jak:



Tutaj s(t), x(t), n(t) i A są odpowiednio źródłami, obserwowanymi danymi, (nieznanym) szumem w danych i (nieznaną) macierzą mieszania, podczas gdy a_i =1,2 ,..., i a i M są kolumnami A. Mieszanie ma być natychmiastowe, więc nie ma opóźnienia czasowego pomiędzy (ukrytą) zmienną źródłową s_i(t) i jest mieszaną w obserwowalną zmienną (danych) x_{j/sub>(t) , gdzie i = 1, 2, ..., M i j = 1, 2, ..., N. Rozważmy, że stochastyczny proces wektorowy {x(t)} ∈ ℝ^N ma średnią E{x(t)}= 0 i macierz kowariancji Cx = {x(t)x(t)^T} . Celem PCA jest aby zidentyfikować strukturę zależności w każdym wymiarze i uzyskać macierz transformacji ortogonalnej W o rozmiarze L×N od ?ℝ^N do ?ℝ^L , L < N , taką, że L-wymiarowy wektor wyjściowy y(t)=W x(t) dostatecznie reprezentuje wewnętrzne cechy danych wejściowych, i gdzie macierz kowariancji Csub>y} z {y (t)} jest macierzą diagonalną D z elementami diagonalnymi ułożonymi w kolejności malejącej, , d_i,j ≥ d_i+1,j+1 . Przywrócenie {x(t)} z {y(t)}, powiedzmy 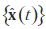, jest w konsekwencji dane wzorem 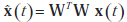. Dla danego L celem PCA jest znalezienie optymalnej wartości W, takiej jak minimalizacja funkcji błędu 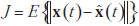. Wiersze w W to PC procesu stochastycznego {x(t)} i wektory własne c_j , 1, 2,...,L wejściowej macierzy kowariancji C_x . Podprzestrzeń rozpięta głównymi wektorami własnymi {c₁,c₂ …c_L} gdzie L < N , nazywana jest podprzestrzenią PCA wymiarowości L. Problem ICA można sformułować następująco: przy danych T realizacjach x(t) , oszacuj zarówno macierz A, jak i odpowiadające jej realizacje s (t). W BSS zadanie jest nieco prostsze i polega na znalezieniu przebiegów {s_i(t} źródeł znających jedynie (obserwowane) mieszaniny {x_j(t)} . Jeśli nie poczyniono żadnych założeń na temat szumu, w (1) pomija się addytywny składnik szumu. Praktyczną strategią jest włączenie szumu do sygnałów jako składnika(ów) uzupełniającego: stąd model ICA przyjmuje postać:

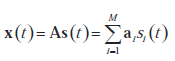Separacja źródeł polega na aktualizacji macierzy rozmieszania B(t), bez odwoływania się do informacji o macierzy mieszania przestrzennego A, tak aby wektor wyjściowy y(t)= B(t) x(t) stał się estymatorem oryginalnych niezależnych sygnałów źródłowych s(t). Macierz rozdzielająca B(t) jest podzielona na dwie części dotyczące zależności w dwóch pierwszych momentach, tj. macierzy wybielającej V(t) oraz zależności w statystyce wyższego rzędu, tj. ortogonalnej macierzy rozdzielającej W(t) w wybielonej przestrzeni. Jeśli założymy, że obserwowane dane x(t) są zerowymi średnimi, to otrzymamy je poprzez wybielanie wektora v(t)= V(t)x(t) dekorelowanymi składnikami. Kolejna transformacja liniowa W(t) szuka rozwiązania poprzez odpowiedni obrót w przestrzeni gęstości składowych i daje y (t )=W(t ) v(t ). Całkowita macierz separacji pomiędzy warstwą wejściową i wyjściową okazuje się być B(t) =W(t) V(t). W standardowym przypadku stacjonarnym wybielanie i ortogonalne macierze separacyjne zbiegają się do pewnych stałych wartości po skończonej liczbie iteracji podczas uczenia, czyli B(t) → B = W V.

IMPLEMENTACJE NEURONALNE

Neuronowe podejście do BSS obejmuje sieć, która ma mieszaniny sygnałów źródłowych na wejściu i generuje przybliżone sygnały źródłowe na wyjściu (rysunek 3). Warunkiem wstępnym jest to, że sygnały wejściowe muszą być wzajemnie nieskorelowane, co jest wymogiem zwykle spełnianym przez PCA. Sygnały wyjściowe muszą jednak być od siebie niezależne, co w naturalny sposób prowadzi z PCA do ICA. Statystyki wyższego rzędu wymagane przez separację źródeł można włączyć do obliczeń bezpośrednio lub poprzez zastosowanie odpowiednich nieliniowości. SSN lepiej pasują do tego drugiego podejścia . Rdzeń dużej klasy neuronowych algorytmów adaptacyjnych składa się z reguły uczenia się i powiązanego z nią kryterium optymalizacji (funkcji celu). Te dwa elementy różnicują algorytmy, które w rzeczywistości są rodzinami algorytmów sparametryzowanych przez zastosowaną funkcję nieliniową. Reguła aktualizacji jest określona przez iteracyjną przyrostową zmianę ΔW macierzy rotacji W, co daje ogólną postać reguły uczenia się:

W → W + ΔW

Neuronowa PCA

Najpierw rozważmy pojedynczy sztuczny neuron otrzymujący M-wymiarowy wektor wejściowy x. Stopniowo dostosowuje swój wektor wag w tak, aby funkcja E{f(w^Tx)} była maksymalizowana, gdzie E jest oczekiwaniem w odniesieniu do (nieznanej) gęstości prawdopodobieństwa x, a f jest ciągłą funkcją celu. Funkcja f jest ograniczona przez ustawienie stałej normy euklidesowej w. Reguła uczenia się z ograniczonym gradientem wznoszenia oparta na sekwencji przykładowych funkcji dla stosunkowo małych szybkości uczenia się α(t) oznacza zatem :

w(t+1)= w(t)+a(t) (I - w(t)Tw(t)) x(t)g(w(t)^Tw(t))

gdzie g = f′ . Wszelkie reguły uczenia się PCA mają tendencję do znajdowania tego kierunku w przestrzeni wejściowej, wzdłuż którego dane mają maksymalną wariancję. Jeśli wszystkie kierunki w przestrzeni wejściowej mają równą wariancję, przypadek jednojednostkowy z odpowiednią nieliniowością w przybliżeniu minimalizuje kurtozę wejścia neuronu. Oznacza to, że wektor wag jednostki będzie wyznaczany przez kierunek w przestrzeni wejściowej, na który rzutowanie danych wejściowych jest w większości skupione i odbiega znacząco od normalności. To zadanie jest zasadniczo celem w technice PP. W przypadku jednowarstwowych sieci ANN składających się z L jednostek równoległych, przy czym każda jednostka i ma ten sam wektor wejściowy M-elementowy x i własny wektor wagowy W_i, które razem tworzą macierz wag M × L W =[w₁ ,w₂,… w_L następująca reguła uczenia uzyskana powyżej jest uogólnieniem liniowej reguły uczenia się PCA (w postaci macierzowej):

W(t+1)= W(t)+a(t) (I - W(t)TW(t)) x(t)g(w(t)^TW(t))

Ze względu na niestabilność powyższego nieliniowej reguły Hebbiana uczenia się dla przypadku wielu jednostek wprowadzono inne podejście polegające na jednoczesnej optymalizacji dwóch kryteriów :

W(t+1)= W(t)+μ(t)(x(t)g(y(t)^T) + γ(t)(I-W(t)W(t)^T))

Tutaj μ(t) jest wybierane jako dodatnie lub ujemne w zależności od tego, czy jesteśmy zainteresowani odpowiednio maksymalizacją lub minimalizacją funkcji celu J₁(w_i = E{f(x^Tw_i)}. Podobnie γ(t) jest kolejnym parametrem wzmocnienia, który jest zawsze dodatni i ogranicza wektory wag do ortonormalności, która jest narzucona przez odpowiednią funkcję kary, taką jak:



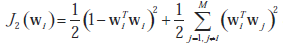
Jest to algorytm bigradientu, który jest iterowany, aż wektory wag osiągną zbieżność z pożądaną dokładnością. Algorytm ten może wykorzystywać znormalizowane uczenie się Hebbiana lub anty-Hebbiana w ujednoliconej formule. Wychodząc od reguły jednej jednostki, wielojednostkowy algorytm bigradientu może jednocześnie wyodrębnić kilka solidnych odpowiedników głównych lub mniejszych wektorów własnych macierzy kowariancji danych . W przypadku wielowarstwowych SSN transfer funkcji ukrytych węzłów można wyrazić radialnymi funkcjami bazowymi (RBF), których parametrów można się nauczyć za pomocą dwustopniowej strategii opadania gradientowego. W celu poprawy wydajności netto stosowana jest nowa, rozwijająca się strategia wstawiania węzłów RBF z różnymi RBF. Podano, że strategia uczenia się oszczędza czas obliczeniowy i przestrzeń pamięci w przybliżeniu mapowań ciągłych i nieciągłych.

Neuronowy ICA

W SSN wdrożono różne formy uczenia się bez nadzoru, wykraczające poza standardowe PCA, takie jak nieliniowe PCA i ICA. Wybielanie danych może być emulowane neuronowo przez PCA za pomocą prostego algorytmu iteracyjnego, który aktualizuje macierz sferyczną V(t):

V(t+1)= V(t)-α(t)(vv^T - I)

Po otrzymaniu macierzy dekorelacji V(t), podstawowym zadaniem algorytmów ICA pozostaje otrzymanie macierzy ortogonalnej W(t ), co jest równoznaczne z odpowiednią rotacją dekorelowanych danych v(t)= V(t)x(t) mające na celu maksymalizację iloczynu gęstości krańcowych jego składników. Istnieją różne podejścia neuronowe do szacowania macierzy rotacji W(t). Ważna klasa algorytmów opiera się na maksymalizacji entropii sieci. Algorytm maksymalizacji informacji nieliniowej BS (infomax) wykonuje online stochastyczne wznoszenie gradientu we wzajemnych informacjach (MI) pomiędzy wyjściami i wejściami sieci. Minimalizując MI pomiędzy wyjściami, sieć rozkłada wejścia na niezależne komponenty. Rozważenie sieci z wektorem wejściowym x(t), macierzą wag W(t) i monotonicznie przekształconym wektorem wyjściowym y=g(Wx+w₀) , to wynikowa reguła uczenia się odpowiednio dla wag i wag błędu systematycznego wynosi:

ΔW= [W^T]^-1 + x(1? 2y)^T a Δw₀ = 1? 2y

W przypadku zmiennych ograniczonych wzajemne oddziaływanie członu antyhebbowskiego x(1?2y)^T i członu przeciwdziałającego rozpadowi [W^T]^-1?? daje gęstość wyjściową bliską płaskiemu rozkładowi stałemu, który odpowiada do maksymalnego rozkładu entropii. Amari, Cichocki i Yang zmienili algorytm BS infomax, wykorzystując gradient naturalny zamiast gradientu stochastycznego, aby zmniejszyć złożoność obliczeń neuronowych i znacząco poprawić szybkość zbieżności. Reguła aktualizacji zaproponowana dla macierzy rozdzielającej to:

ΔW= [I - g(Wx) (Wx)^T]W

Lee rozszerzył zarówno na rozkłady sub-, jak i supergaussowskie, regułę uczenia się opracowaną na podstawie zasady infomax spełniającą ogólne kryterium stabilności i zachowującą prosty początkową architekturę sieci. Stosując do optymalizacji gradient naturalny lub względny , ich zasada uczenia się daje wyniki, które konkurują z obliczeniami wsadowymi o stałym punkcie. Algorytm ekwiwariantnej separacji adaptacyjnej poprzez niezależność (EASI) wprowadzony przez Cardoso i Lahelda (1996) jest nieliniową metodą dekorelacji. Funkcja celu J(W)= E{f(Wx)} poddawana jest minimalizacji przy zastosowaniu ograniczenia ortogonalnego nałożonego na W i nieliniowości g = f′ wybranej według kurtozy danych. Podstawowa zasada aktualizacji jest równa:

ΔW= ?λ (yy^T ? I + g (y)y^T ? yg (y^T ))W

Algorytmy stałoprzecinkowe (FP) przeszukują rozwiązanie ICA poprzez minimalizację wzajemnych informacji (MI) pomiędzy estymowanymi komponentami. Reguła uczenia się FastICA znajduje kierunek w taki, że rzut w^Tx maksymalizuje funkcję kontrastu postaci J_G(w) = [E{f(w^T)} - E{f(v)}]², gdzie v oznacza standaryzowaną zmienną Gaussa. Reguła uczenia się jest w zasadzie metodą dekorelacji podobną do metody Grama-Schmidta.

OCENA ALGORYTMU

Porównawczo uruchamiamy algorytmy neuronowe PCA i ICA, korzystając z syntetycznie wygenerowanych szeregów czasowych, zepsutych addytywnie pewnym białym szumem, aby złagodzić ścisły determinizm . Od tego czasu neuronowa PCA została zaimplementowana przy użyciu algorytmu bigradient działa to zarówno w przypadku minimalizacji, jak i maksymalizacji kryterium J₁ w ramach ograniczeń normalności narzuconych przez funkcję kary J₂. Algorytmy neuronowe ICA obejmowały rozszerzony infomax Bella i Sejnowskiego, póładaptacyjny stałoprzecinkowy szybki algorytm ICA, zaadaptowany wariant algorytmu EASI zoptymalizowany pod kątem danych rzeczywistych oraz rozszerzony uogólniony rozkład lambda (EGLD ) algorytm oparty na maksymalnej wiarygodności. W przypadku źródeł sztucznie generowanych dokładność wyodrębnienia źródeł ukrytych przez algorytm wykonujący ICA można mierzyć za pomocą pewnych wskaźników ilościowych. Pierwszy, którego użyliśmy, został zdefiniowany jako stosunek sygnału do zakłóceń (SIR):



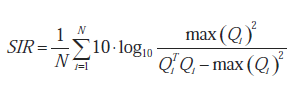
gdzie Q = BA jest ogólną macierzą transformacji ukrytych składników źródła, i Q jest i-tą kolumną Q, max(Q_i) jest maksymalnym elementem Q_i, a N jest liczbą sygnałów źródłowych. Im wyższy jest SIR, tym lepsza jest skuteczność separacji algorytmu. Drugim zastosowanym wskaźnikiem była odległość pomiędzy całkowitą macierzą transformującą Q a idealną macierzą permutacji, którą interpretuje się jako błąd przesłuchu (CTE):



Powyżej Q_ij jest ij-tym elementem Q, max |Q_i|jest maksymalnym elementem wiersza i w Q o maksymalnej wartości bezwzględnej, a max |Q_j| jest elementem kolumny j w Q o maksymalnej wartości bezwzględnej. Macierz permutacji to zdefiniowany tak, że w każdym z jego wierszy i kolumn tylko jeden z elementów jest równy jedności, podczas gdy wszystkie pozostałe elementy są równe zero. Oznacza to, że CTE osiąga minimalną wartość zero dla dokładnej macierzy permutacji (tj. doskonałego rozkładu) i wzrasta dodatnio, im bardziej Q odbiega od macierzy permutacji (tj. rozkładu o mniejszej dokładności). Zdefiniowaliśmy względny błąd wyszukiwania sygnału (SRE) jako odległość euklidesową między sygnałami źródłowymi a ich najlepiej dopasowanymi estymowanymi składowymi, znormalizowaną do liczby sygnałów źródłowych, razy liczbę próbek czasowych, i razy moduł sygnałów źródłowych:



Im niższy jest SRE, tym lepiej szacunki przybliżają ukryte sygnały źródłowe. Stabilizowana wersja algorytmu FastICA jest atrakcyjna ze względu na szybką i niezawodną zbieżność oraz brak parametrów wymagających dostrajania. Naturalny gradient zawarty w rozszerzonym infomaxie BS działa lepiej niż oryginalne wznoszenie gradientowe i jest mniej wymagający obliczeniowo. Chociaż algorytm BS jest teoretycznie optymalny w sensie traktowania wzajemnych informacji jako funkcji celu, podobnie jak wszystkie neuronowe algorytmy bez nadzoru, jego działanie w dużym stopniu zależy od szybkości uczenia się, a jego zbieżność jest raczej powolna. Algorytm EGLD oddziela rozkłady skośne, nawet dla zerowej kurtozy. Pod względem czasu obliczeń najszybszy był rozszerzony algorytm infomax BS, FastICA wierniej pobierał źródła spośród wszystkich testowanych algorytmów, natomiast algorytm EASI wyszedł z macierzą pełnej transformacji Q, która jest najbliższa jedności.

PRZYSZŁE TRENDY

Metody neuromorficzne w analizie eksploracyjnej i eksploracji danych to szybko pojawiające się zastosowania nienadzorowanego treningu neuronowego. W ostatnich latach zaproponowano nowe algorytmy uczenia się, jednak ich właściwości teoretyczne, zakres optymalnego zastosowania i ocena porównawcza pozostają w dużej mierze niezbadane. Z używanymi algorytmami uczącymi nie są powiązane żadne twierdzenia o zbieżności. Co więcej, zbieżność algorytmów w dużym stopniu zależy od właściwego wyboru szybkości uczenia się i nawet po osiągnięciu zbieżności algorytmy neuronowe są stosunkowo powolne w porównaniu z obliczeniami typu wsadowego. Oczekuje się, że nieliniowy i niestacjonarny neuronowy ICA zostanie opracowany dzięki niealgorytmicznemu przetwarzaniu SSN i ich zdolności do uczenia się relacji nieanalitycznych, jeśli zostaną odpowiednio przeszkolone.

WNIOSEK

Zarówno PCA, jak i ICA mają pewne wspólne cechy, takie jak skupienie się na budowaniu modeli generatywnych, które prawdopodobnie wygenerowały zaobserwowane dane, oraz zachowanie informacji i redukcja redundancji. W podejściu neuromorficznym parametry modelu traktowane są jako wagi sieci, które zmieniają się w procesie uczenia. Główna trudność w aproksymacji funkcji wynika z wyboru parametrów sieci, które należy ustalić a priori oraz tych, których należy się nauczyć za pomocą odpowiedniej reguły szkoleniowej. PCA i ICA mają główne zastosowania w eksploracji danych i eksploracyjnej analizie danych, takich jak charakterystyka sygnału, ekstrakcja optymalnych cech i kompresja danych, a także stanowią podstawę klasyfikatorów podprzestrzennych w rozpoznawaniu wzorców. ICA jest znacznie lepiej dopasowana niż PCA do wykonywania BSS, ślepej dekonwolucji i wyrównywania.

WSTĘP

Przed pojawieniem się inżynierii oprogramowania brak miejsca w pamięci w komputerach i brak ustalonych metod programowania skłoniły pierwszych programistów do stosowania samodzielnych modyfikacji jako zwykłej strategii kodowania. Chociaż rozwiązania wykorzystujące samomodyfikację były nieuniknione i cenne dla tej grupy oprogramowania, okazały się niewystarczające, podczas gdy programy rosły pod względem rozmiaru i złożoności, a bezpieczeństwo i niezawodność stały się głównymi wymaganiami. Inżynieria oprogramowania w latach 70. niemal doprowadziła do zaniku samomodyfikującego się oprogramowania, którego występowanie później ograniczono do małych, niskopoziomowych programów w języku maszynowym o bardzo specjalnych wymaganiach. Niemniej jednak najnowsze badania w tej dziedzinie oraz współczesne zapotrzebowanie na wydajne i skuteczne sposoby reprezentowania i obsługi złożonych zjawisk w komputerach zaawansowanych technologii powodują, że w kilku sytuacjach samomodyfikację należy ponownie rozważyć jako wybór wdrożeniowy. Sztuczna inteligencja znacząco przyczyniła się do realizacji tego scenariusza, opracowując i stosując niekonwencjonalne podejścia, m.in. heurystyka, reprezentacja i obsługa wiedzy, metody wnioskowania, ewolucja oprogramowania/sprzętu, algorytmy genetyczne, sieci neuronowe, systemy rozmyte, systemy ekspertowe, uczenie maszynowe itp. W tej publikacji zaproponowano inną alternatywę dla rozwoju aplikacji sztucznej inteligencji: wykorzystanie adaptacyjnych urządzeń, specjalna klasa abstrakcji, której praktyczne zastosowanie w rozwiązywaniu bieżących problemów nazywa się technologią adaptacyjną. Zachowanie urządzeń adaptacyjnych jest definiowane przez dynamiczny zestaw reguł. W takim przypadku wiedza może być reprezentowana, przechowywana i obsługiwana w ramach tego zestawu reguł poprzez dodawanie i usuwanie reguł reprezentujących dodanie lub wyeliminowanie informacji, które reprezentują. Ze względu na wyraźny sposób reprezentacji i zdobywania wiedzy, adaptacyjność zapewnia bardzo prostą abstrakcję dla wdrożenia mechanizmów sztucznego uczenia się: wiedzę można wygodnie gromadzić poprzez wstawianie i usuwanie reguł oraz zarządzać nią poprzez śledzenie ewolucji zestawu reguł i interpretowanie zebranych informacji jako reprezentacji wiedzy zakodowanej w zbiorze reguł.

GŁÓWNY TEMAT TEGO ARTYKUŁU

W artykule przedstawiono koncepcje i podstawy dotyczące adaptacyjności i technologii adaptacyjnej, podano ogólne sformułowanie stosowanych abstrakcji adaptacyjnych oraz wskazano ich główne zastosowania. Pokazuje, jak urządzenia sterowane regułami mogą zamienić się w urządzenia adaptacyjne do zastosowania w modelowaniu systemów uczenia się i wprowadza niedawno sformułowany rodzaj abstrakcji adaptacyjnych posiadających adaptacyjne urządzenia znajdujące się obok. Ta nowatorska funkcja może być cenna przy wdrażaniu metauczenia się, ponieważ umożliwia urządzeniom adaptacyjnym dynamiczną zmianę sposobu, w jaki modyfikują swój własny zestaw definiujących reguł. Znaczną ilość informacji na temat adaptacyjności i tematów pokrewnych można znaleźć na stronie internetowej (strona internetowa LTA).

TŁO

W tej sekcji podsumowano podstawy adaptacyjności i ustalono ogólne sformułowanie adaptacyjnych urządzeń sterowanych regułami (Neto, 2001), przy czym brak adaptacji jest jedynym ograniczeniem nałożonym na urządzenie znajdujące się poniżej. Do studiów i badań nad adaptacją i technologią adaptacyjną pożądana jest pewna wiedza teoretyczna: języki formalne, gramatyki, automaty, modele obliczeniowe, abstrakcje oparte na regułach i tematy pokrewne. Niemniej jednak, czy to do celów programistycznych, czy do pierwszego kontaktu z tematem, opanowanie podstaw adaptacyjności może nie być problematyczne, nawet nie mając wcześniejszej wiedzy z zakresu teorii komputerów. W abstrakcjach adaptacyjnych adaptacyjność można osiągnąć poprzez dołączenie działań adaptacyjnych do wybranych reguł wybranych ze zbioru reguł definiującego jakieś znajdujące się poniżej urządzenie nieadaptacyjne. Działania adaptacyjne umożliwiają urządzeniom adaptacyjnym dynamiczną zmianę swojego zachowania bez pomocy z zewnątrz, poprzez modyfikację własnego zestawu reguł definiujących za każdym razem, gdy wykonywana jest nadrzędna reguła. Ze względów praktycznych dozwolone są maksymalnie dwie akcje adaptacyjne: jedna wykonywana przed wykonaniem podstawowej reguły, a druga po niej. Urządzenie adaptacyjne zachowuje się tak, jakby było częściowo nieadaptacyjne: zaczynając od konfiguracji początkowego urządzenia bazowego, wykonuje następujące dwa kroki, aż do osiągnięcia dobrze określonej konfiguracji końcowej:

•  Jeśli nie jest wykonywana żadna akcja adaptacyjna, uruchom podstawowe urządzenie;
•  Zmodyfikuj zbiór reguł definiujących urządzenie, wykonując akcję adaptacyjną.

Urządzenia oparte na regułach

Urządzenie sterowane regułami to dowolna abstrakcja formalna, której zachowanie jest opisane przez zestaw reguł, który odwzorowuje każdą możliwą konfigurację urządzenia na odpowiednią następną. Urządzenie jest deterministyczne, gdy dla dowolnej konfiguracji i dowolnego wejścia możliwa jest pojedyncza następna konfiguracja. W przeciwnym razie mówi się, że jest niedeterministyczny. Urządzenia niedeterministyczne umożliwiają wiele ważnych możliwości dla każdego ruchu i wymagają cofania się, dlatego w praktyce zwykle preferowane są deterministyczne odpowiedniki. Zakładać, że:

•  D jest urządzeniem sterowanym regułami, zdefiniowanym jako D = (C,R,S,c₀, A) .
•  C jest zbiorem możliwych konfiguracji.
•  R ⊆ C ×(S ⋃{ ε})×C to zbiór reguł opisujących jego zachowanie, gdzie e oznacza bodziec pusty, niereprezentujący żadnego zdarzenia.
•  S jest zbiorem ważnych bodźców wejściowych.
•  ₀ ∈C to jego konfiguracja początkowa.
•  A ⊆ C jest zbiorem jego konfiguracji końcowych.

Niech c₁ ⇒^(r) c_(i+1) (w skrócie c₁ ⇒ c_{i + 1}) oznacza zastosowanie jakiejś reguły r = (c_i, s. c>sub>i+1 ) ∈ R , do aktualnej konfiguracji c_i w odpowiedzi na jakiś bodziec wejściowy s ∈ S ⋃{ε }, co daje następną konfigurację c _i+1 . Kolejne zastosowania reguł w odpowiedzi na a to strumień w ∈ S^* bodźców wejściowych rozpoczynający się od konfiguracji początkowej c₀ i prowadzący do konfiguracji końcowej c ∈ A oznaczamy c₀ ⇒^*_wc (Operator postfiksu gwiazdy we wzorach oznacza zamknięcie Kleene′a: jego poprzedni element może zostać ponownie utworzony lub zastosowany dowolną liczbę razy). Mówimy, że D definiuje zdanie w wtedy i tylko wtedy, gdyc₀ ⇒^*_wzachodzi dla pewnego c ∈ A. Zbiór L(D) wszystkich takich zdań nazywany jest językiem zdefiniowanym przez D: L(D) = {w ∈ S^* | c₀ ⇒^*_wc ,c ∈ A}

Urządzenia adaptacyjne (opierające się na regułach).

Adaptacyjne urządzenie sterowane regułami AD (ND₀ , AM) kojarzy początkowe, sąsiadujące urządzenie sterowane regułami ND0<.sub> (C,NR₀, S,c,₀A) , z pewnym mechanizmem adaptacyjnym AM, który może dynamicznie zmieniać swoje zachowanie poprzez modyfikację jego definiujących reguł. Osiąga się to poprzez wykonanie niezerowych działań adaptacyjnych wybranych z zestawu AA działań adaptacyjnych, co obejmuje zerową akcję adaptacyjną a₀. Wbudowany licznik t zaczyna się od 0 i jest automatycznie zwiększany po wykonaniu wszelkich działań adaptacyjnych. Niech X_j oznacza wartość X po j wykonaniach działań adaptacyjnych przez AD. Działania adaptacyjne w funkcjach wywołania AA, które odwzorowują bieżący zestaw reguł adaptacyjnych AD AR_tna AR_t+1 poprzez wstawianie i usuwanie reguł adaptacyjnych ar z AM. Niech AR będzie zbiorem wszystkich możliwych zbiorów adaptacyjnych zasady AD. Dowolny a^k ∈ A odwzorowuje bieżący zestaw reguł &iisin; AR AR na ∈ AR _{t +1}AR: a_{k : AR &rarrr; AR AM kojarzy się z każdą regułą nr p ∈? NR urządzenia bazowego AD ND para działań adaptac}yjnych bap ,aap ∈ AA :

AM ⊆ AA × NR × AA

Notacja

Pisząc elementarne akcje adaptacyjne, ?[ar], + [ar] i - [ar] oznaczają odpowiednio wyszukiwanie, wstawianie i eliminowanie reguł adaptacyjnych zgodnych z szablonem ar. Należy pamiętać, że ar może zawierać odniesienia do parametrów, zmiennych i generatorów, aby umożliwić tworzenie odniesień pomiędzy podstawowymi działaniami adaptacyjnymi wewnątrz funkcji adaptacyjnej. Mając podstawową regułę nr^p ∈ NR, definiujemy regułę adaptacyjną ar^p ∈ AM jako: ar^p = (ba^p,nr^p,aa^p) . Dla każdego ruchu AD, AM stosuje pewien ar^p w trzech krokach:

A. wykonanie akcji adaptacyjnej ba^p przed zastosowaniem reguły nr^p
B. zastosowanie podstawowej zasady nieadaptacyjnej nr^p
C. wykonanie akcji adaptacyjnej aa^p

Poniższy algorytm szkicuje ogólne działanie AD:

1. Zainicjuj c₀, w;
2. Jeśli w jest wyczerpane, przejdź do 7, w przeciwnym razie zdobądź następne wydarzenie st;
3. Dla bieżącej konfiguracji c_t określ zestaw CR reguł zgodnych z c_t
A. jeśli CR = ∅, odrzuć w.
B. jeśli CR = {(c_t, s, c′)} , zastosuj (c_t, s, c′) jak w krokach
4-6, prowadząc AD do c_t+1 = c′ .
C. jeśli CR = {r^k = (c_t,s,c^k)| c^k ∈ C k =1, …,n, n >1} , zastosuj wszystkie reguły r^k równolegle, jak w krokach 4-6, prowadząc AD odpowiednio do c¹,c²,…,cⁿ.
4. Jeśli ba^p = a⁰, przejdź do 2, w przeciwnym razie zastosuj pierwszy bap. Jeśli reguła ar^p została usunięta przez ba^p, przejdź do 3, przerywając ar^p, w przeciwnym razie AD osiągnął konfigurację pośrednią, przejdź do 2.
5. Zastosuj nr^p do bieżącej (pośredniej) konfiguracji, uzyskując nową konfigurację pośrednią;
6. Zastosuj aa^p, uzyskując następną (stabilną) konfigurację AD; idź do 2
7. Jeżeli zostało osiągnięte jakieś c_t+1 ∈ F , to AD akceptuje w, w przeciwnym razie AD odrzuca w; zatrzymywać się

Hierarchiczne, wielopoziomowe urządzenia adaptacyjne

Zdefiniujmy bardziej rozbudowane urządzenie adaptacyjne, uogólniając powyższą definicję. Wywołaj urządzenia nieadaptacyjne urządzeniami poziomu 0; zdefiniuj urządzenia poziomu 1, posiadające sąsiadujące urządzenia poziomu 0, do których każdej reguły dołączona jest para działań adaptacyjnych poziomu 1. Niech urządzenie znajdujące się obok będzie urządzeniem adaptacyjnym poziomu k. Można skonstruować urządzenie poziomu (k+1), dołączając parę działań adaptacyjnych na poziomie (k+1) do każdej z jego reguł. Jest to krok wprowadzający do definicji wielopoziomowych urządzeń adaptacyjnych o strukturze hierarchicznej. Poza zbiorem reguł definiujących podporządkowane urządzenie poziomu k, dla k > 0, podporządkowane urządzenie z funkcjami adaptacyjnymi działa na swoim własnym poziomie, który może wykorzystywać działania adaptacyjne poziomu (k+1) do modyfikowania zachowania adaptacyjnego poziomu k Funkcje. Zatem dla k > 0 urządzenia poziomu (k+1) mogą zmieniać sposób, w jaki modyfikują się znajdujące się obok nich urządzenia poziomu k. Dotyczy to również k = 1, ponieważ nawet dla k = 0 (pusty) zbiór funkcji adaptacyjnych nadal istnieje.

Notacja

Brak działań adaptacyjnych w regułach nieadaptacyjnych nr jest wyraźnie wyrażany poprzez podanie wszystkich reguł poziomu 0 r⁰ w postaci (a⁰ nr a⁰). Dlatego reguły poziomu k r_k przyjmują ogólny format (b_k,r_k-1, a_k , z działaniami adaptacyjnymi zarówno b_k, jak i a_k na poziomie k dla dowolnego poziomu adaptacyjnego k ≥ 0 . Zatem wszystkie zasady definiujące urządzenia adaptacyjne poziomu k są podane w standardowej formie



z



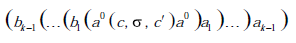
eprezentujący jedną z reguł definiujących urządzenie adaptacyjne na niższym poziomie (k - 1). Dlatego działania adaptacyjne poziomu i mogą modyfikować zarówno zbiór reguł adaptacyjnych poziomu i oraz zbiór elementarnych działań adaptacyjnych definiujących funkcje adaptacyjne poziomu (i - 1).

PROSTY PRZYKŁAD ILUSTRACYJNY

W poniższym przykładzie zastosowano notację graficzną dla przejrzystości i zwięzłości. Podczas rysowania automatów (jak zwykle) okręgi reprezentują stany; kółka z podwójną linią oznaczają stany końcowe; strzałki wskazują przejścia; etykiety na strzałkach wskazują żetony zużyte przez przejście i (opcjonalnie) powiązaną akcję adaptacyjną. Reprezentując funkcje adaptacyjne, fragmenty automatów w nawiasach oznaczają grupę przejść, które należy dodać (+) lub usunąć (-), gdy zostanie zastosowana akcja adaptacyjna. Rysunek przedstawia początkowy kształt automatu adaptacyjnego, który akceptuje aⁿb²ⁿc³ⁿ, n ≥0.



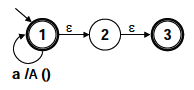
W stanie 1 to zawiera przejście zużywające a, które wykonuje akcję adaptacyjną A( ). Rysunek definiuje sposób działania A():



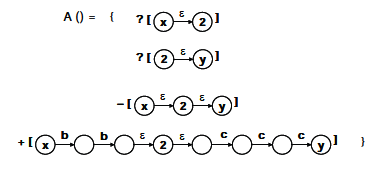
•  Używając stanu 2 jako odniesienia, wyeliminuj puste przejścia używając stanów x i y
•  Dodaj sekwencję zaczynającą się od x, z dwoma przejściami zużywającymi b
•  Dołącz sekwencję dwóch pustych przejść dzielących stan 2
Dołącz sekwencję z trzema przejściami zużywającymi c, kończąc na y.

Rysunek przedstawia dwie pierwsze zmiany kształtu tego automatu po zużyciu dwóch pierwszych symboli a (w stanie 1) w zdaniu a²b⁴c⁶. W swym ostatnim kształcie automat w trywialny sposób pochłania pozostałe b⁴c⁶


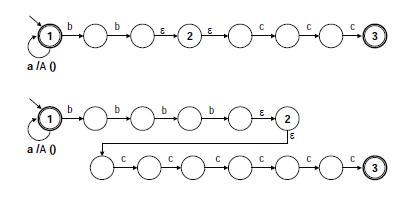
Reprezentacja wiedzy

Powyższy przykład ilustruje, jak urządzenia adaptacyjne wykorzystują zestaw reguł jako jedyny element do reprezentowania i obsługi wiedzy. Reguła (tutaj przejście) może obsługiwać parametryczne informacje zawarte w jego komponentach (w tym przypadku stany początkowe i docelowe przejścia, token oznaczający przejście, wywoływana przez nie funkcja adaptacyjna itp.). Reguły można łączyć ze sobą w celu przedstawienia nieelementarnych informacji (w tym przypadku sekwencje przejść wykorzystujących żetony "b" i "c" śledzą wartość n w każdym konkretnym zdaniu). W ten sposób reguły i ich komponenty mogą działać i mogą być interpretowane jako elementy wiedzy niskiego poziomu. Chociaż nie da się narzucić zasad dotyczących reprezentowania i obsługi wiedzy w systemach reprezentowanych za pomocą urządzeń adaptacyjnych, szczegóły procesu uczenia się można dobrać zgodnie ze szczególnymi potrzebami każdego modelowanego systemu. W praktyce zachowanie uczenia się urządzenia adaptacyjnego można zidentyfikować i zmierzyć, śledząc postęp zbioru reguł w trakcie jego działania i interpretując dynamikę jego zmian. W powyższym przykładzie, gdy przejścia są dodawane do automatu poprzez wykonanie akcji adaptacyjnej A ( ), można zinterpretować długość sekwencji przejść zużywających "b" (lub "c") jako przejaw gromadzonej wiedzy przez automat adaptacyjny na wartość n (jego dokładna wartość staje się dostępna po zużyciu podciągu tokenów "a").

PRZYSZŁE TRENDY

Abstrakcje adaptacyjne stanowią znaczący postęp teoretyczny w informatyce poprzez wprowadzenie i badanie potężnych nieklasycznych koncepcji, takich jak: zachowanie zmienne w czasie, autonomicznie dynamiczne zestawy reguł, hierarchia wielopoziomowa, statyczne i dynamiczne adaptacyjne działania. Koncepcje te pozwalają na ustalenie stylu modelowania, odpowiedniego do opisu złożonych systemów uczenia się, skutecznego rozwiązywania tradycyjnie trudnych problemów, radzenia sobie z samomodyfikującymi się metodami uczenia się oraz zapewniania języków i środowisk komputerowych do wygodnego opracowywania programów jakościowych o dynamicznie zmiennym zachowaniu. Wszystkie te cechy są niezbędne do opracowywania, modelowania, projektowanie i wdrażanie aplikacji w Sztucznej Inteligencji, która korzysta z adaptacyjności, jednocześnie wyrażając tradycyjnie trudne do opisania fakty związane ze Sztuczną Inteligencją. Poniżej wymieniono funkcje, które Technologia Adaptacyjna oferuje dla kilku dziedzin obliczeń, w szczególności związanych ze sztuczną inteligencją, ze wskazaniem ich głównych wpływów i zastosowań.

•  Technologia Adaptacyjna zapewnia prawdziwy model obliczeniowy zbudowany na formalnych podstawach. Większość stosowanych technik sztucznej inteligencji jest bardzo trudna do wyrażenia i naśladowania, ponieważ powiązanie między elementami modeli a informacjami, które reprezentują, jest często ukryte, dlatego też rozumowanie ich działania jest trudne do prześledzenia i zaplanowania przez człowieka. Adaptacyjne urządzenia oparte na regułach koncentrują całą zgromadzoną wiedzę w swoich regułach, a całą logikę obsługującą takie informacje w swoich działaniach adaptacyjnych. Takie właściwości otwierają dla Sztucznej Inteligencji możliwość obserwacji, rozumieć i kontrolować zjawiska modelowane przez urządzenia adaptacyjne. Śledząc i interpretując, jak i dlaczego zachodzą zmiany w zestawie reguł urządzenia, a także śledząc semantykę działań adaptacyjnych, można może wywnioskować uzasadnienie reakcji modelu na jego dane wejściowe.
•  Urządzenia adaptacyjne mają wystarczającą moc obliczeniową, aby modelować złożone obliczenia. W (Neto, 2000) przedstawiono kilka udanych przypadków użycia z prostymi i wydajnymi urządzeniami adaptacyjnymi stosowanymi zamiast złożonych, tradycyjnych formuł.
•  Urządzenia Adaptacyjne to modele obliczeniowe równoważne maszynie Turinga, które można wykorzystać do konstruowania pełnych specyfikacji języków programowania w pojedynczym zapisie, włączając kwestie leksykalne, składniowe, kontekstowo-zależne kwestie statyczno-semantyczne, funkcje wbudowane w język, takie jak operacje arytmetyczne, biblioteki, semantyka, generowanie i optymalizacja kodu, interpretacja kodu w czasie wykonywania itp.
•  Urządzenia adaptacyjne dobrze nadają się do reprezentowania złożonych języków, w tym idiomów. Język naturalny szczególnie wymaga wyrażenia i obsługi kilku cech, takich jak fleksja słów, ortografia, wiele form składni, porządkowanie fraz, elipsa, permutacja, niejednoznaczności, anafora i inne. Kilka prostych technik pozwala urządzeniom adaptacyjnym radzić sobie z takimi elementami, znacznie upraszczając wysiłek związany z ich reprezentowaniem i przetwarzaniem. Zastosowania są szerokie, w tym tłumaczenie maszynowe, eksploracja danych, konwersja tekstu na głos i głos na tekst itp.
• o Sztuka komputerowa to kolejne fascynujące potencjalne zastosowanie urządzeń adaptacyjnych. Muzyka i inne formy wyrazu artystycznego są formami ludzkiego języka. Biorąc pod uwagę niektóre opisy języków, komputery mogą wychwytywać ludzkie umiejętności i automatycznie generuj interesujące wyniki. Przeprowadzono udane eksperymenty w dziedzinie muzyki, z doskonałymi wynikami.
•  Systemy podejmowania decyzji mogą wykorzystywać adaptacyjne tablice i drzewa decyzyjne do konstruowania inteligentnych systemów, które akceptują wzorce uczenia się, uczą się, jak je klasyfikować, a zatem klasyfikują nieznane wzory. Do pomyślnie udanych eksperymentów należą: klasyfikacja wzorów geometrycznych, dekodowanie języków migowych, lokalizowanie wzorców na obrazach, generowanie diagnoz na podstawie objawów i danych medycznych itp.
•  Wnioskowanie językowe wykorzystuje urządzenia adaptacyjne do generowania formalnych opisów języków na podstawie próbek, poprzez identyfikowanie i zbieranie informacji strukturalnych oraz uogólnianie na podstawie dowodów dotyczących konstrukcji powtarzalnych lub rekurencyjnych.
•  Urządzenia Adaptacyjne mogą być wykorzystywane do celów edukacyjnych poprzez przechowywanie zebranych informacji na temat monitorowanego zjawiska. W systemach edukacyjnych zachowanie zarówno uczniów, jak i trenerów można wywnioskować i wykorzystać do podjęcia decyzji o dalszym postępowaniu.
•  Można skonstruować Urządzenia Adaptacyjne, których podstawową abstrakcją jest język komputerowy. Instrukcje w takich językach można uważać za reguły określające zachowanie programu. Dołączając reguły adaptacyjne do instrukcji, program staje się samomodyfikowalny. Aby aplikacje adaptacyjne mogły wyrażać się w sposób naturalny, potrzebne są języki adaptacyjne. Aby adaptacyjność stała się prawdziwym stylem programowania, należy opracować techniki i metody konstruowania dobrego oprogramowania adaptacyjnego, ponieważ dotychczasowe aplikacje adaptacyjne były zwykle tworzone w sposób ściśle doraźny.

WNIOSEK

Technologia Adaptacyjna dotyczy technik, metod i tematów odnoszących się do rzeczywistego zastosowania adaptacyjności. Automaty adaptacyjne zostały po raz pierwszy zaproponowane do praktycznej reprezentacji języków kontekstowych . Gramatyki adaptacyjne zostały wykorzystane jako jego generatywne odpowiedniki . Do specyfikacji i analizy układów reaktywnych czasu rzeczywistego opracowano prace w oparciu o adaptacyjne wersje schematów stanu. Ciekawym potwierdzeniem mocy i użyteczności urządzeń adaptacyjnych do modelowania złożonych systemów było udane zastosowanie Adaptacyjnych Łańcuchów Markowa w komputerowym urządzeniu generującym muzykę . Adaptacyjne tablice decyzyjne (Neto, 2001) i adaptacyjne drzewa decyzyjne są obecnie eksperymentowane w aplikacjach do podejmowania decyzji. Donoszono o eksperymentach badających potencjał urządzeń adaptacyjnych do konstruowania systemów wnioskowania językowego . Ważnym obszarem, w którym urządzenia adaptacyjne wykazują swoją siłę, jest specyfikacja i przetwarzanie języków naturalnych . Reprezentując syntaktyczne zależności kontekstowe języka naturalnego, osiąga się wiele innych wyników. Symulacja i modelowanie inteligentnych systemów to kolejne konkretne zastosowania formalizmów adaptacyjnych, co ilustruje opis mechanizmu sterującego inteligentnego pojazdu autonomicznego, który zbiera informacje ze swojego otoczenia i buduje mapy do nawigacji. Możliwych jest wiele innych zastosowań urządzeń adaptacyjnych w kilku dziedzinach.
Adaptacyjność: Właściwość struktur, które dynamicznie i autonomicznie zmieniają swoje zachowanie w odpowiedzi na bodźce wejściowe.
Adaptacyjny model obliczeniowy: abstrakcja o dużej mocy Turinga, która naśladuje zachowanie potencjalnie samomodyfikujących się złożonych systemów.
Urządzenie adaptacyjne: Struktura zachowująca się dynamicznie, z umieszczonym obok urządzeniem i mechanizmem adaptacyjnym.
Funkcje adaptacyjne i akcje adaptacyjne: Akcje adaptacyjne to wywołania funkcji adaptacyjnych, które mogą określić zmiany, jakie należy wprowadzić w zestawie reguł danej warstwy oraz w funkcjach adaptacyjnych warstwy znajdującej się bezpośrednio pod nimi.
Mechanizm adaptacyjny: dyscyplina zmian powiązana z zestawem reguł urządzenia adaptacyjnego, która zmienia zachowanie urządzenia znajdującego się obok niego poprzez wykonywanie działań adaptacyjnych.
Adaptacyjne urządzenie oparte na regułach: urządzenie adaptacyjne, którego zachowanie jest określone przez dynamicznie zmieniający się zestaw reguł, np.: automaty adaptacyjne, gramatyki adaptacyjne itp.
Zależność od kontekstu: reinterpretacja terminów ze względu na warunki występujące w innym miejscu zdania, np. zasady umowy w języku angielskim, sprawdzanie typu w Pascalu. Formalizm kontekstowy (zależny): abstrakcja zdolna do reprezentowania języków Chomsky′ego typu 1 lub typu 0. Do wyrażania takich języków dobrze nadają się automaty adaptacyjne i adaptacyjne gramatyki bezkontekstowe.
Hierarchiczne (wielopoziomowe) urządzenie adaptacyjne: warstwowe struktury adaptacyjne, w których działania adaptacyjne warstwy mogą modyfikować zarówno reguły własnej warstwy, jak i funkcje adaptacyjne warstwy podstawowej.
Urządzenie sąsiadujące (lub bazowe): dowolne urządzenie wykorzystywane jako podstawa do formułowania urządzeń adaptacyjnych. Najbardziej wewnętrzna część wielopoziomowego urządzenia znajdującego się poniżej nie może być adaptacyjna

WSTĘP

Eksploracja reguł asocjacyjnych (ARM) jest jednym z ważnych zadań eksploracji danych, które zostało szeroko zbadane przez społeczność eksploracji danych i znalazło szerokie zastosowanie w przemyśle. Reguła asocjacyjna to wzorzec, który implikuje współwystępowanie zdarzeń lub elementów w bazie danych. Wiedza o takich relacjach w bazie danych może być wykorzystana w strategicznym podejmowaniu decyzji zarówno w domenach komercyjnych, jak i naukowych. Typowym zastosowaniem ARM jest analiza koszyka rynkowego, w której odkrywane są powiązania między różnymi elementami w celu analizy nawyków zakupowych klienta. Odkrycie takich powiązań może pomóc w opracowaniu lepszych strategii marketingowych. ARM było szeroko stosowane w innych zastosowaniach, takich jak przestrzenno-czasowe, opieka zdrowotna, bioinformatyka, dane internetowe itp. Reguła asocjacyjna jest implikacją formy X → Y, gdzie X i Y są niezależnymi zestawami atrybutów/elementów. Reguła asocjacyjna wskazuje, że jeśli zestaw elementów X występuje w rekordzie transakcji, to zestaw elementów Y również występuje w tym samym rekordzie. X nazywane jest poprzednikiem reguły, a Y nazywane jest następnikiem reguły. Przetwarzanie ogromnych zestawów danych w celu odkrywania współwystępujących elementów i generowanie interesujących reguł w rozsądnym czasie jest celem wszystkich algorytmów ARM. Zadanie odkrywania współwystępujących zestawów elementów nie może być łatwo wykonane przy użyciu języka SQL, co ujawni krótka refleksja. Użycie zapytania agregującego "Count" wymaga określenia warunku w klauzuli where, która znajduje częstotliwość tylko jednego zestawu elementów na raz. Aby znaleźć wszystkie zestawy współwystępujących elementów w bazie danych z n elementami, liczba zapytań, które należy napisać, jest wykładnicza w n. Jest to główna motywacja do projektowania algorytmów do wydajnego odkrywania współwystępujących zestawów elementów, które są wymagane do znalezienia reguł asocjacyjnych. W tym artykule skupiamy się na algorytmach eksploracji reguł asocjacyjnych (ARM) i problemach skalowalności w ARM. Zakładamy, że czytelnik jest zaznajomiony z motywacją i zastosowaniami eksploracji reguł asocjacyjnych

KONTEKST

Niech I = {i₁, i₂, … , i_n} oznacza zbiór elementów, a D oznacza bazę danych N transakcji. Typowa transakcja T ∈ D może zawierać podzbiór X całego zbioru elementów I i jest powiązana z unikalnym identyfikatorem TID. Zbiór elementów to zbiór jednego lub większej liczby elementów, tj. X jest zbiorem elementów, jeśli X ⊆ I. Zbiór k-elementów to zbiór elementów o kardynalności k. Transakcja zawiera zbiór elementów X, jeśli X ⊆ T. Wsparcie zbioru elementów X, zwane również Pokryciem, to ułamek transakcji, które zawierają X. Oznacza ono prawdopodobieństwo, że transakcja zawiera X. N

Wsparcie(X ) = P(X ) = Liczba transakcji zawierających X / N

Zbiór elementów mający wsparcie większe niż określony przez użytkownika próg wsparcia (ms) jest znany jako częsty zestaw elementów. Reguła asocjacyjna jest implikacją postaci X →Y [Wsparcie, Pewność], gdzie X ⊂ I, Y ⊂ I i X ∩Y = ∅, gdzie Wsparcie i Pewność są metrykami oceny reguły. Wsparcie reguły X → Y w D wynosi "S", jeśli S% transakcji w D zawiera X ∪ Y. Oblicza się je jako:

Wsparcie (X → Y) = P(X ∪ Y) = Liczba transakcji zawierających X ∪ Y

Wsparcie wskazuje na powszechność reguły. W typowej aplikacji analizy koszyka rynkowego reguły o bardzo niskich wartościach wsparcia reprezentują rzadkie zdarzenia i prawdopodobnie będą nieciekawe lub nieopłacalne. Pewność reguły mierzy jej siłę i dostarcza wskazówki na temat niezawodności przewidywań dokonanych przez regułę. Reguła X → Y ma pewność "C" w D, jeśli C % transakcji w D, które zawierają X, zawiera również Y. Pewność jest obliczana jako warunkowe prawdopodobieństwo wystąpienia Y w transakcji, zakładając, że X jest obecne w tej samej transakcji, tj.

Pewność (X → Y) = P(X/Y) = P(X∪Y)/P(X) = Wsparcie(X∪Y)/Wsparcie(X)

Reguła wygenerowana z częstych zestawów elementów jest silna, jeśli jej pewność jest większa niż określony przez użytkownika próg pewności (mc). Celem algorytmów eksploracji reguł asocjacyjnych jest odkrycie zestawu silnych reguł z danej bazy danych zgodnie z określonymi przez użytkownika progami ms i mc. Algorytmy dla ARM zasadniczo wykonują dwa odrębne zadania: (1) Odkrywanie częstych zestawów elementów. (2) Generowanie silnych reguł z częstych zestawów elementów. Pierwsze zadanie wymaga zliczenia zestawów elementów w bazie danych i filtrowania według określonego przez użytkownika progu (ms). Drugie zadanie generowania reguł z częstych zestawów elementów to prosty proces generowania podzbiorów i sprawdzania siły. Poniżej opisujemy ogólne podejścia do znajdowania częstych zestawów elementów w algorytmach eksploracji reguł asocjacyjnych. Drugie zadanie jest trywialne, jak wyjaśniono w ostatniej sekcji artykułu.

PODEJŚCIA DO GENEROWANIA CZĘSTO BIORĄCYCH UDZIAŁ ELEMENTÓW

Jeśli zastosujemy podejście siłowe, aby odkryć częste zestawy elementów, algorytm musi utrzymywać liczniki dla wszystkich 2ⁿ - 1 zestawów elementów. W przypadku dużych wartości n, które są wspólne dla zestawów danych będących celem eksploracji, utrzymanie tak dużej liczby liczników jest zniechęcającym zadaniem. Nawet jeśli założymy dostępność tak dużej pamięci, indeksowanie tych liczników również stanowi wyzwanie. Badacze eksploracji danych opracowali liczne algorytmy do efektywnego odkrywania częstych zestawów elementów. Wcześniejsze algorytmy dla ARM odkryły wszystkie częste zestawy elementów. Później trzy niezależne grupy badaczy wykazały, że wystarczy odkryć częste zamknięte zestawy elementów (FCI) zamiast wszystkich częstych zestawów elementów (FI). FCI to zestawy elementów, których wsparcie nie jest równe wsparciu żadnego z ich właściwych superzbiorów. FCI to zredukowana, kompletna i bezstratna reprezentacja częstych zestawów elementów. Ponieważ FCI są znacznie mniej liczne niż FI, koszty obliczeniowe dla ARM są drastycznie zmniejszone. Rysunek 2 podsumowuje różne podejścia stosowane dla ARM. Krótko opisujemy te podejścia.

Odkrywanie częstych zestawów elementów

Podejście poziomowe

Algorytmy poziomowe zaczynają się od znalezienia zestawów elementów o kardynalności jeden i stopniowo przechodzą do częstych zestawów elementów o wyższej kardynalności. Algorytmy te wykorzystują antymonotoniczną własność częstych zestawów elementów, zgodnie z którą żaden nadzbiór rzadkiego zestawu elementów nie może być częsty. Agarwal i inni zaproponowali algorytm Apriori, który jest najpopularniejszym algorytmem iteracyjnym w tej kategorii. Zaczyna się od znalezienia częstych zestawów elementów o rozmiarze jeden i przechodzi poziom po poziomie, znajdując kandydujące zestawy elementów o rozmiarze k przez łączenie zestawów elementów o rozmiarze k-1. Dwa zestawy elementów, każdy o rozmiarze k-1, łączą się, tworząc zestaw elementów o rozmiarze k wtedy i tylko wtedy, gdy mają pierwsze k-2 wspólne elementy. Na każdym poziomie algorytm przycina zestawy elementów kandydackich, używając własności antymonotonicznej, a następnie skanuje bazę danych, aby znaleźć wsparcie przyciętych zestawów elementów kandydackich. Proces ten trwa, dopóki zestaw częstych zestawów elementów nie będzie pusty. Ponieważ każda iteracja wymaga skanowania bazy danych, maksymalna liczba wymaganych skanów bazy danych jest taka sama jak rozmiar maksymalnego zestawu elementów. Dwa główne wąskie gardła w algorytmie Apriori to i) liczba przejść i ii) liczba wygenerowanych kandydatów. Pierwsze prawdopodobnie spowoduje wąskie gardło wejścia/wyjścia, a drugie spowoduje duże obciążenie pamięci i wykorzystanie procesora. Naukowcy zaproponowali rozwiązania tych problemów ze znacznym powodzeniem. Chociaż szczegółowa dyskusja na temat tych rozwiązań wykracza poza zakres tego artykułu, konieczna jest krótka wzmianka. Techniki haszujące zmniejszają liczbę kandydatów poprzez utworzenie tablicy haszującej i odrzucenie kontenera, jeśli ma on wsparcie mniejsze niż ms. W ten sposób na każdym poziomie zapotrzebowanie na pamięć jest zmniejszane ze względu na mniejszy zestaw kandydatów. Redukcja jest najbardziej znacząca na niższych poziomach. Prowadzenie listy identyfikatorów transakcji dla każdego zestawu kandydatów zmniejsza dostęp do bazy danych. Algorytm dynamicznego zliczania zestawów elementów zmniejsza liczbę skanów poprzez zliczanie zestawów kandydatów o różnej kardynalności w jednym skanie . Algorytm Pincer Search wykorzystuje dwukierunkową strategię do przycinania zestawu kandydatów od góry (maksymalny) i od dołu (zestaw 1-elementowy). Strategie partycjonowania i próbkowania zostały również zaproponowane w celu przyspieszenia zadania zliczania.

Algorytmy oparte na drzewie

Zaproponowano algorytmy oparte na drzewie, aby przezwyciężyć problem wielokrotnych skanów bazy danych. Algorytmy te kompresują (czasem stratnie) bazę danych do struktury danych drzewa i znacznie zmniejszają liczbę skanów bazy danych. Następnie drzewo jest używane do eksploracji w celu obsługi wszystkich częstych zestawów elementów. Drzewo wyliczeniowe używane w algorytmie Max Miner porządkuje zestawy kandydatów podczas wyszukiwania maksymalnych częstych zestawów elementów. Struktura danych ułatwia szybką identyfikację długich częstych zestawów elementów na podstawie informacji zebranych podczas każdego przejścia. Algorytm jest szczególnie odpowiedni dla gęstych baz danych z maksymalnymi zestawami elementów o wysokiej kardynalności. Han i inni zaproponowali algorytm wzrostu wzorca częstego (FP), który wykonuje skanowanie bazy danych i znajduje częste zestawy elementów o kardynalności jeden. Układa wszystkie częste zestawy elementów w tabeli (nagłówek) w kolejności malejącej według ich wsparcia. Podczas drugiego skanowania bazy danych algorytm konstruuje strukturę danych w pamięci zwaną FP-Tree, wstawiając każdą transakcję po jej ponownym uporządkowaniu w kolejności malejącej według wsparcia. Węzeł w FP-Tree przechowuje pojedynczy atrybut, tak aby każda ścieżka w drzewie reprezentowała i zliczała odpowiadający jej rekord w bazie danych. Łącze z nagłówka łączy wszystkie węzły elementu. Te informacje strukturalne są wykorzystywane podczas eksploracji FP-Tree. Algorytm FP-Growth rekurencyjnie generuje poddrzewa z FP-Trees odpowiadające każdemu częstemu zestawowi elementów. Coenen i inni zaproponowali struktury danych Total Support Tree (T-Tree) i Partial Support Tree (P-Tree), które oferują znaczną przewagę pod względem przechowywania i wykonywania. Tego rodzaju struktury danych to skompresowane drzewa wyliczeniowe zbiorów, które powstają po jednym przeskanowaniu bazy danych i przechowują wszystkie zestawy elementów jako oddzielne rekordy w bazie danych.

Odkrycie częstych zamkniętych zestawów elementów podejście poziomowe

Pasquier i inni zaproponowali metodę Close w celu znalezienia częstych zamkniętych zestawów elementów (FCI). Ta metoda znajduje zamknięcia na podstawie operatorów domknięć Galois i oblicza generatory. Operator domknięć Galois h(X) dla pewnego X ⊆ I jest zdefiniowany jako przecięcie transakcji w D zawierających zestaw elementów X. Zestaw elementów X jest domkniętym zestawem elementów wtedy i tylko wtedy, gdy h(X) = X. Jeden z najmniejszych dowolnie wybranych zestawów elementów p, taki że h(p) = X, jest znany jako generator X. Metoda Close opiera się na algorytmie Apriori. Zaczyna się od 1- zestawów elementów, znajduje domknięcie na podstawie operatora domknięć Galois, przechodzi poziom po poziomie, obliczając generatory i ich domknięcia (tj. FCI) na każdym poziomie. Na każdym poziomie zestawy elementów generatora kandydatów o rozmiarze k są znajdowane przez łączenie zestawów elementów generatora o rozmiarze k-1 przy użyciu procedury kombinatorycznej używanej w algorytmie Apriori. Generatory kandydatów są przycinane przy użyciu dwóch strategii: i) usuń generatory kandydatów, których wszystkie podzbiory nie są częste ii) usuń generatory kandydatów, jeśli domknięcie jednego z jego podzbiorów jest nadzbiorem generatora. Następnie algorytm znajduje wsparcie przyciętego generatora kandydatów. Każda iteracja wymaga jednego przejścia przez bazę danych w celu skonstruowania zbioru FCI i zliczenia ich wsparcia.

Podejście oparte na drzewie

Wang i inni zaproponowali algorytm Closet+ do obliczania FCI i ich wsparcia przy użyciu struktury drzewa FP. Algorytm opiera się na strategii dziel i zwyciężaj i oblicza lokalne częste elementy pewnego prefiksu poprzez budowanie i skanowanie jego rzutowanej bazy danych.

Podejście oparte na kratownicy pojęć

Kratownica pojęć jest podstawową strukturą formalnej analizy pojęć (FCA). FCA jest gałęzią matematyki opartą na pojęciach i hierarchiach pojęć. Pojęcie (A, B) jest definiowane jako para zestawu obiektów A (znanego jako zakres) i zestawu atrybutów B (znanego jako intencja) tak, że zestaw wszystkich atrybutów należących do zakresu A jest taki sam jak B, a zestaw wszystkich obiektów zawierających atrybuty intencji B jest taki sam jak A. Innymi słowy, żaden obiekt inny niż obiekty zestawu A nie zawiera wszystkich atrybutów B i żaden atrybut inny niż atrybuty w zestawie B nie jest zawarty we wszystkich obiektach zestawu A. Kratka pojęć jest kompletną kratownicą wszystkich pojęć. Stumme G. (1999) odkrył, że intencja B pojęcia (A, B) reprezentuje zamknięty zestaw elementów, co oznacza, że wszystkie algorytmy znajdowania pojęć mogą być używane do znajdowania zamkniętych zestawów elementów. Kuznetsov S.O. i Obiedkov S.A. (2002) przedstawiają porównanie wydajności różnych algorytmów dla pojęć. Naiwna metoda obliczania pojęć, zaproponowana przez Gantera, jest podana w Załączniku A. Ta metoda generuje wszystkie pojęcia, tj. wszystkie zamknięte zestawy elementów. Zamknięte zestawy elementów wygenerowane za pomocą tej metody w przykładzie 1 to {A},{B},{C},{A,B},{A,C},{B,D},{B, C,D}, {B,D,E}, {B,C,D,E}. Częste zamknięte zestawy elementów to {A},{B},{C},{B,D},{B,C,D},{B,D,E}.

Generowanie reguł asocjacyjnych

Gdy znane są wszystkie częste zestawy elementów, reguły asocjacyjne można wygenerować w prosty sposób, znajdując wszystkie podzbiory zestawów elementów i testując ich siłę . Na podstawie powyższego algorytmu silne reguły wygenerowane z BCD częstych zestawów elementów w Przykładzie 1 to: BC → D, conf=100% CD → B, conf=100% gdzie mc = 70% Istnieją dwa sposoby znalezienia reguł asocjacyjnych z częstych zamkniętych zestawów elementów: i) obliczenie częstych zestawów elementów z FCI, a następnie znalezienie reguł asocjacyjnych ii) wygenerowanie reguł bezpośrednio za pomocą FCI. Metoda Close wykorzystuje pierwsze podejście, które generuje wiele redundantnych reguł, podczas gdy metoda zaproponowana przez Zaki wykorzystuje drugie podejście i wywodzi reguły bezpośrednio z kratownicy koncepcji. Wywodzące się w ten sposób reguły asocjacyjne są regułami nieredundantnymi. Na przykład, zbiór silnych reguł wygenerowany przy użyciu metody Close w Przykładzie 1 to {BC → D,CD →B,D →B,E → B,E →D,E → BD, BE →D,DE →B}. W tym samym przykładzie zbiór nieredundantnych silnych reguł wygenerowany przy użyciu podejścia kratownicy koncepcji to {D →B, E → BD, BC → D, CD → B}. Możemy tutaj zaobserwować, że wszystkie reguły można wyprowadzić ze zredukowanego nieredundantnego zbioru reguł.

Problemy skalowalności w eksploracji reguł asocjacyjnych

Problemy skalowalności w ARM zmotywowały rozwój algorytmów przyrostowych i równoległych. Algorytmy przyrostowe dla ARM zachowują liczbę wybranych zestawów elementów i ponownie wykorzystują tę wiedzę później, aby odkryć częste zestawy elementów z rozszerzonej bazy danych. Algorytm szybkiej aktualizacji (FUP) jest najwcześniejszym algorytmem opartym na tym pomyśle. Później przedstawiono różne algorytmy oparte na próbkowaniu. Algorytmy równoległe partycjonują albo zbiór danych do zliczania, albo zbiór liczników, na różne maadd chines, aby osiągnąć skalowalność . Algorytmy, które partycjonują zbiór danych, wymieniają liczniki, podczas gdy algorytmy, które partycjonują liczniki, wymieniają zbiory danych, ponosząc wysokie koszty komunikacji.

PRZYSZŁE TRENDY

Odkrycie częstych zamkniętych zestawów elementów (FCI) jest dużym osiągnięciem w algorytmach ARM. Przy obecnym tempie wzrostu baz danych i rosnących zastosowaniach ARM w różnych zastosowaniach naukowych i komercyjnych przewidujemy ogromny zakres badań nad równoległymi, przyrostowymi i rozproszonymi algorytmami dla FCI. Wykorzystanie struktury kratowej dla FCI daje obietnicę skalowalności. Eksploracja online na strumieniowych zestawach danych przy użyciu podejścia FCI jest interesującym kierunkiem prac.

WNIOSEK

Artykuł przedstawia podstawowe podejście do eksploracji reguł asocjacyjnych, skupiając się na niektórych typowych algorytmach znajdowania częstych zestawów elementów i częstych zamkniętych zestawów elementów. Omówiono różne podejścia do znajdowania takich zestawów elementów. Omówiono również podejście formalnej analizy koncepcji do znajdowania częstych zamkniętych zestawów elementów. Krótko omówiono generowanie reguł z częstych zestawów elementów i częstych zamkniętych zestawów elementów. Artykuł porusza kwestie skalowalności związane z różnymi algorytmami.

WSTĘP

W ostatnich latach wiele badań i wysiłków rozwojowych skierowano na szerokie pole inteligencji otoczenia (AmI), a ten trend ma się utrzymać w przewidywalnej przyszłości. AmI ma na celu płynną integrację usług w ramach inteligentnych infrastruktur, które mają być używane w domu, w pracy, w samochodzie, w podróży i ogólnie w większości środowisk zamieszkiwanych przez ludzi. Jest to stosunkowo nowy paradygmat zakorzeniony w komputerach wszechobecnych, który wymaga integracji i konwergencji wielu dyscyplin, takich jak sieci czujników, urządzenia przenośne, inteligentne systemy, interakcje człowiek-komputer i interakcje społeczne, a także wielu technik w ramach sztucznej inteligencji, takich jak planowanie, rozumowanie kontekstowe, rozpoznawanie mowy, tłumaczenie języków, uczenie się, adaptacyjność oraz rozumowanie czasowe i hipotetyczne. Termin AmI został wymyślony przez Komisję Europejską, gdy w 2001 r. jedna z jej Grup Doradczych Programu zainicjowała wyzwanie AmI , później zaktualizowane w 2003 r. Ale chociaż termin AmI pochodzi z Europy, cele pracy zostały przyjęte na całym świecie, patrz na przykład (The Aware Home, 2007), (The Oxygen Project, 2007) i (The Sony Interaction Lab, 2007). Podstawy infrastruktury AmI opierają się na imponującym postępie, którego jesteśmy świadkami w technologiach bezprzewodowych, sieciach czujników, możliwościach wyświetlania, prędkościach przetwarzania i usługach mobilnych. Te osiągnięcia pomagają zapewnić wiele przydatnych (wierszowych) informacji dla aplikacji AmI. Potrzebny jest dalszy postęp w pełnym wykorzystaniu takich informacji, aby zapewnić przewidziany stopień inteligencji, elastyczności i naturalności. To właśnie tutaj sztuczna inteligencja i techniki wieloagentowe odgrywają ważną rolę. W tym artykule dokonamy przeglądu postępu, jaki został osiągnięty w dziedzinie systemów inteligentnych, omówimy rolę sztucznej inteligencji i technologii agentowych oraz skupimy się na zastosowaniu AmI w niezależnym życiu

TŁO

Inteligencja otoczenia to wizja społeczeństwa informacyjnego, w którym normalne środowiska pracy i życia są otoczone wbudowanymi inteligentnymi urządzeniami, które mogą dyskretnie łączyć się z tłem i działać za pośrednictwem intuicyjnych interfejsów. Takie urządzenia, z których każde specjalizuje się w jednej lub większej liczbie możliwości, mają współpracować w ramach infrastruktury inteligentnych systemów, aby zapewnić wiele usług mających na celu ogólną poprawę bezpieczeństwa i ochrony oraz poprawę jakości życia w zwykłych środowiskach życia, podróży i pracy. Komisja Europejska zidentyfikowała cztery scenariusze AmI , aby pobudzić wyobraźnię oraz zainicjować i ustrukturyzować badania w tej dziedzinie. Podsumowujemy dwa z nich, aby nadać smak wizjom AmI.

Scenariusze AmI:

1. Dimitrios robi sobie przerwę na kawę i woli, żeby mu nie przeszkadzano. Nosi na sobie lub ciele aktywowany głosem cyfrowy awatar, znany jako Digital Me (D-Me). D-Me jest zarówno urządzeniem uczącym się, poznającym Dimitriosa i jego otoczenie, jak i działającym urządzeniem oferującym funkcje komunikacji, przetwarzania i podejmowania decyzji. Podczas przerwy na kawę D-Me odbiera przychodzące połączenia i wiadomości e-mail Dimitriosa. Robi to płynnie w niezbędnych językach, odtwarzając głos i akcent Dimitriosa. Następnie D-Me odbiera połączenie od żony Dimitriosa, rozpoznaje jego pilność i przekazuje je Demetriosowi. Jednocześnie odbiera wiadomość od D-Me starszej osoby, znajdującej się w pobliżu. Ta osoba wyszła z domu bez swoich leków i chciałaby dowiedzieć się, gdzie uzyskać dostęp do podobnych leków. Poprosił swojego D-Me, w języku naturalnym, o zbadanie tej sprawy. Dimitrios cierpi na podobne problemy zdrowotne i przyjmuje te same leki. Jego D-Me przetwarza przychodzące żądanie informacji i decyduje się nie ujawniać tożsamości Dimitriosa ani nie oferować bezpośredniej pomocy, ale dostarczyć D-Me osoby starszej listę najbliższych aptek i potencjalny kontakt z grupą samopomocową. Carmen planuje swoją podróż do pracy. Prosi AmI, za pomocą komendy głosowej, aby znalazł dla niej kogoś, z kim mogłaby dzielić podwózkę do pracy w pół godziny. Następnie planuje przyjęcie, które ma wydać tego wieczoru. Chce upiec ciasto, a jej lodówka elektroniczna wyświetla przepis na ekranie lodówki i podświetla brakujące składniki. Carmen uzupełnia swoją listę zakupów na ekranie i prosi o dostarczenie jej do najbliższego punktu dystrybucji w jej okolicy. Wszystkie towary są inteligentnie oznaczone, więc może sprawdzać postęp swoich wirtualnych zakupów z dowolnego włączonego urządzenia w dowolnym miejscu i wprowadzać zmiany. Carmen podróżuje do pracy samochodem z dynamicznymi funkcjami kierowania ruchem drogowym i systemami ruchu drogowego, które dynamicznie dostosowują ograniczenia prędkości w zależności od natężenia ruchu i poziomu zanieczyszczenia. Kiedy wraca do domu, AmI wita ją i sugeruje, że następnego dnia powinna pracować zdalnie, ponieważ w centrum miasta planowana jest duża demonstracja.

2. Potrzeby, które napędzają AmI i zapewniają możliwości, dotyczą poprawy bezpieczeństwa i jakości życia, zwiększenia produktywności i jakości produktów i usług, w tym usług publicznych, takich jak szpitale, szkoły, wojsko i policja, oraz innowacji przemysłowych. AmI ma ułatwiać kontakty międzyludzkie oraz ulepszać społeczność i kulturę, a ostatecznie powinno inspirować zaufanie i pewność. Niektóre technologie wymagane dla AmI zostały podsumowane na rysunku 1. Praca AmI opiera się na wszechobecnych technologiach obliczeniowych, sieciach czujników i technologiach mobilnych. Aby zapewnić wymaganą inteligencję i naturalność, uważamy, że znaczący wkład może pochodzić z postępów w dziedzinie sztucznej inteligencji i technologii agentów. Sztuczna inteligencja ma długą historię badań nad planowaniem, harmonogramowaniem, rozumowaniem czasowym, diagnostyką błędów, rozumowaniem hipotetycznym i rozumowaniem z niekompletnymi i niepewnymi informacjami. Wszystkie te techniki mogą przyczynić się do AmI, w którym działania i decyzje muszą być podejmowane w czasie rzeczywistym, często z dynamiczną i niepewną wiedzą o środowisku i użytkowniku. Badania nad technologią agentów koncentrowały się na architekturach agentów, które łączą kilka, często poznawczych, możliwości, w tym reaktywność i adaptacyjność, a także tworzenie społeczeństw agentów poprzez komunikację, normy i protokoły. Ostatnie prace próbowały wykorzystać te techniki dla AmI. W (Augusto i Nugent 2004) zbadano wykorzystanie rozumowania temporalnego w połączeniu z aktywnymi bazami danych w kontekście inteligentnych domów. W (Sadri 2007) zbadano wykorzystanie rozumowania temporalnego razem z agentami w celu radzenia sobie z podobnymi scenariuszami, w których oceniane są informacje obserwowane w środowisku domowym, rozpoznawane są odchylenia od normalnego zachowania i ryzykowne sytuacje oraz zalecane są działania kompensacyjne. Związek AmI z agentami poznawczymi jest motywowany przez (Stathis i Toni 2004), którzy twierdzą, że logika obliczeniowa podnosi poziom systemu do poziomu użytkownika. Popierają model agenta KGP , aby zbadać, jak pomóc podróżnemu działać niezależnie i bezpiecznie w nieznanym otoczeniu, korzystając z osobistego komunikatora. Augusto i inni zajmują się procesem podejmowania decyzji w obliczu sprzecznych opcji. (Li i Ji 2005) oferują nowe ramy probabilistyczne oparte na sieciach bayesowskich do radzenia sobie z niejednoznacznymi i niepewnymi obserwacjami sensorycznymi oraz zmieniającymi się stanami użytkowników, aby zapewnić prawidłową pomoc. Amigoni i inni zajmują się zorientowanym na cel aspektem aplikacji AmI, a w szczególności problemem planowania w AmI. Wnioskują, że wymagane jest połączenie scentralizowanych i rozproszonych możliwości planowania ze względu na rozproszoną naturę AmI i udział heterogenicznych agentów o różnych możliwościach. Oferują podejście oparte na Hierarchical Task Networks, przyjmując perspektywę paradygmatu wieloagentowego dla AmI. Paradygmat osadzonych agentów dla środowisk AmI, ze szczególnym uwzględnieniem opracowywania technik uczenia się i adaptacji dla agentów. Każdy agent jest wyposażony w czujniki i efektory i wykorzystuje system uczenia się oparty na logice rozmytej. Prawdziwe środowisko AmI w formie "inteligentnego akademika" jest wykorzystywane do eksperymentów. Prywatność i bezpieczeństwo w kontekście aplikacji AmI w domu, w pracy oraz w domenach zdrowia, zakupów i mobilności omówiono w (Friedewald 2007). W przypadku takich zastosowań biorą pod uwagę zagrożenia bezpieczeństwa, takie jak inwigilacja użytkowników, kradzież tożsamości i złośliwe ataki, a także potencjalne wykluczenie cyfrowe wśród społeczności i presję społeczną.

INTELIGENCJA OTOCZENIA DLA NIEZALEŻNEGO ŻYCIA

Jednym z głównych zastosowań AmI jest wspieranie usług na rzecz niezależnego życia, przedłużanie czasu, w którym ludzie mogą żyć przyzwoicie we własnych domach, zwiększając ich autonomię i pewność siebie. Może to obejmować eliminację monotonnych codziennych czynności, monitorowanie i opiekę nad osobami starszymi, zapewnianie bezpieczeństwa lub oszczędzanie zasobów. Celem takich zastosowań AmI jest pomoc w:

* utrzymaniu bezpieczeństwa osoby poprzez monitorowanie jej otoczenia, rozpoznawanie i przewidywanie zagrożeń oraz podejmowanie odpowiednich działań,
* zapewnianie pomocy w codziennych czynnościach i wymaganiach, na przykład poprzez przypominanie i doradzanie w sprawie leków i odżywiania, oraz
* poprawa jakości życia, na przykład poprzez dostarczanie spersonalizowanych informacji o rozrywce i zajęciach towarzyskich.

Obszar ten przyciągnął wiele uwagi w ostatnich latach ze względu na zwiększoną długowieczność i starzenie się populacji w wielu częściach świata. Aby taki system AmI był użyteczny i akceptowany, musi być wszechstronny, adaptowalny, zdolny do radzenia sobie ze zmieniającymi się środowiskami i sytuacjami, przejrzysty i łatwy, a nawet przyjemny w interakcji. Wierzymy, że obiecujące byłoby zbadanie podejścia opartego na zapewnieniu architektury agenta składającej się ze społeczeństwa heterogenicznych, inteligentnych, osadzonych agentów, z których każdy specjalizuje się w jednej lub większej liczbie funkcjonalności. Agenci powinni być zdolni do dzielenia się informacjami poprzez komunikację, a ich dialogi i zachowania powinny być regulowane przez zależne od kontekstu i dynamiczne normy. Podstawowe możliwości inteligentnych agentów obejmują:

Wyczuwanie: aby umożliwić agentowi obserwowanie środowiska Reaktywność: aby zapewnić zależne od kontekstu dynamiczne zachowanie i zdolność do adaptacji do zmian w środowisku
Planowanie: aby zapewnić zachowanie ukierunkowane na cel Decyzja o celu: aby umożliwić dynamiczne decyzje o tym, które cele mają wyższe priorytety
Wykonywanie akcji: aby umożliwić agentowi wpływanie na środowisko. Wszystkie te funkcjonalności wymagają również rozumowania o ograniczeniach czasoprzestrzennych odzwierciedlających środowisko, w którym działa system AmI.

Większość tych funkcjonalności została zintegrowana w modelu KGP . Włączenie zachowań normatywnych zostało omówione w (Sadr 2006), gdzie rozważamy również, jak wybierać spośród różnych typów celów, w zależności od norm rządzących. Aby zapoznać się z ogólną dyskusją na temat znaczenia norm w sztucznych społeczeństwach, zobacz (Pitt, 2005). Agenci KGP są umiejscowieni w środowisku za pośrednictwem swoich możliwości fizycznych. Informacje otrzymane ze środowiska (w tym od innych agentów) aktualizują stan agenta i dostarczają danych wejściowych do jego teorii cyklu dynamicznego, która z kolei określa kolejne kroki pod względem swoich przejść, wykorzystując swoje możliwości rozumowania.

PRZYSZŁE TRENDY

Jak większość innych technologii informacyjnych i komunikacyjnych, AmI prawdopodobnie nie będzie samo w sobie dobre ani złe, ale jego wartość będzie oceniana na podstawie różnych sposobów, w jakie technologia będzie wykorzystywana do poprawy życia ludzi. W tej sekcji omawiamy nowe możliwości i wyzwania dla integracji AmI z tym, co ludzie robią w zwykłych warunkach. Abstrahujemy od trendów sprzętowych i skupiamy się na obszarach związanych z oprogramowaniem, które prawdopodobnie odegrają ważną rolę w przyjęciu technologii AmI. Punktem centralnym jest obserwacja, że ludzie odkrywają i rozumieją świat poprzez interakcje wizualne i konwersacyjne. W rezultacie w nadchodzących latach spodziewamy się, że projektowanie systemów AmI będzie się koncentrować na sposobach, które pozwolą ludziom na interakcję w naturalny sposób, wykorzystując ich wspólne umiejętności, takie jak mówienie, gestykulacja, spoglądanie. Ten rodzaj naturalnej interakcji uzupełni istniejące interfejsy i będzie wymagał, aby systemy AmI były zdolne do reprezentowania obiektów wirtualnych, być może w 3D, a także do rejestrowania ruchów ludzi w otoczeniu i identyfikowania, które z tych ruchów są kierowane do obiektów wirtualnych. Oczekujemy również nowych badań ukierunkowanych na przetwarzanie danych z czujników z różnymi informacjami i różnymi rodzajami formatów, takimi jak audio, wideo i RFID. Wydajne techniki indeksowania, wyszukiwania i strukturyzacji tych danych oraz sposoby ich przekształcania w semantyczne informacje wyższego poziomu wymagane przez agentów poznawczych będą ważnym obszarem przyszłych prac. Podobnie, odwrotna strona tego procesu prawdopodobnie będzie równie ważna, a mianowicie, jak tłumaczyć informacje wyższego poziomu na sygnały niższego poziomu wymagane przez siłowniki znajdujące się w otoczeniu. Biorąc pod uwagę, że czujniki i siłowniki zapewnią połączenie ze środowiskiem fizycznym, przewidujemy również dalsze badania w celu zajęcia się ogólnym łączeniem systemów AmI z już istniejącymi infrastrukturami obliczeniowymi, takimi jak sieć semantyczna. Niniejsza praca stworzy hybrydowe środowiska, które będą musiały łączyć użyteczne informacje z istniejących technologii przewodowych z informacjami z technologii bezprzewodowych. Aby umożliwić tworzenie takich środowisk, wyobrażamy sobie potrzebę zbudowania nowych ram i oprogramowania pośredniczącego, aby ułatwić integrację heterogenicznych systemów AmI i uczynić interoperacyjność bardziej elastyczną. Inną ważną kwestią jest to, w jaki sposób ludzkie doświadczenie w AmI będzie zarządzane w sposób, który będzie możliwie jak najbardziej dyskretny. Przewidujemy, że rozwój systemów poznawczych odegra bardzo ważną rolę. Chociaż będzie wiele obszarów zachowań systemów poznawczych, które będą musiały zostać uwzględnione, przewidujemy, że rozwój modeli agentów, które dostosowują się i uczą , będzie miał ogromne znaczenie. Wyzwaniem tutaj będzie to, jak zintegrować wynik tych zdolności adaptacyjnych i uczących się z procesami rozumowania i podejmowania decyzji przez agenta. Wynikające z tego zachowanie poznawcze musi rozróżniać nowo poznane koncepcje od istniejących, a także rozróżniać normalne zachowanie od wyjątków. Oczekujemy, że AmI wyłoni się wraz z formowaniem społeczności użytkowników, którzy mieszkają i pracują w określonej lokalizacji. Wówczas pojawia się problem zarządzania wszystkimi informacjami, które są dostarczane i przechwytywane w miarę rozwoju systemu. Przewidujemy, że badania będą dotyczyć takich kwestii, jak semantyczne adnotacje treści oraz partycjonowanie i własność informacji. Łączenie lokalnych społeczności z inteligentnymi domami, e-zdrowiem, handlem mobilnym i systemami transportowymi ostatecznie doprowadzi do powstania globalnego systemu AmI. Aby aplikacje w takim systemie zostały przyjęte przez ludzi, będziemy musieli zobaczyć konkretne badania czynników ludzkich, aby zdecydować, jak dyskretne, akceptowalne i pożądane wydają się działania środowiska AmI osobom, które z nich korzystają. Niektóre badania czynników ludzkich powinny koncentrować się na kwestiach prezentacji obiektów i agentów w środowisku 3D, a także na ważnych kwestiach prywatności, zaufania i bezpieczeństwa. Aby umożliwić dostosowanie interakcji systemu do różnych klas użytkowników, konieczne jest pozyskanie i przechowywanie informacji o tych użytkownikach. Aby zatem ludzie mogli zaufać interakcjom AmI w przyszłości, musimy zadbać o to, aby wszechobecne inteligentne środowisko zachowywało prywatność w sposób etyczny. Etyczne lub, lepiej, normatywne zachowanie nie może być zapewnione tylko na poziomie poznawczym, ale także na niższym, wdrażającym poziomie platformy AmI. W tym kontekście zapewnienie, że przekazywane informacje są szyfrowane, certyfikowane i przestrzegają przejrzystych zasad bezpieczeństwa, będzie wymagane do budowania systemów mniej podatnych na złośliwe ataki. Na koniec przewidujemy również zmiany w modelach biznesowych, które charakteryzowałyby interakcje AmI

WNIOSEK

Sukces adopcji AmI opiera się na odpowiednim połączeniu wszechobecnego przetwarzania, sztucznej inteligencji i technologii agentów. Przydatną klasą aplikacji, które mogą przetestować takie połączenie, jest AmI wspierające niezależne życie. W przypadku takich aplikacji zidentyfikowaliśmy trendy, które prawdopodobnie odegrają ważną rolę w przyszłości.

WSTĘP

Według rscheearch w Cmabrigde Uinervtisy, nie jest ważne, w jakiej kolejności znajdują się litery w słowie, jedyną ważną rzeczą jest, aby pierwsze i drugie litery znajdowały się na właściwym miejscu. Dzieje się tak, ponieważ ludzkie umysły nie są rozpatrywane przez każdego czytelnika, ale przez słowo jako wlohe. Niestety systemy komputerowe nie są jeszcze tak inteligentne jak ludzki umysł. W ciągu ostatnich kilku lat znaczna liczba badaczy skupiła się na analizie zakłóconego tekstu. Zakłócone dane tekstowe można znaleźć w nieformalnych środowiskach (czat online, SMS, e-maile, tablice ogłoszeń itp.) oraz w tekście generowanym przez automatyczne rozpoznawanie mowy lub systemy optycznego rozpoznawania znaków. Zakłócenie może potencjalnie pogorszyć wydajność innych algorytmów przetwarzania informacji, takich jak klasyfikacja, klasteryzacja, podsumowywanie i ekstrakcja informacji. Określimy niektóre kluczowe obszary badań nad zaszumionym tekstem i przedstawimy krótki przegląd stanu wiedzy. Obszary te to: (i) klasyfikacja zaszumionego tekstu, (ii) korygowanie zaszumionego tekstu, (iii) ekstrakcja informacji z zaszumionego tekstu. Pierwszy z nich omówimy w tym rozdziale, a dwa kolejne w następnym. Zaszumienie w tekście definiujemy jako jakąkolwiek różnicę w formie powierzchniowej tekstu elektronicznego w stosunku do zamierzonego, poprawnego lub oryginalnego tekstu. Codziennie widzimy takie zaszumione teksty w różnych formach. Każdy z nich ma unikalne cechy i dlatego wymaga specjalnego traktowania. W tej sekcji przedstawiamy niektóre takie formy zaszumionych danych tekstowych.
Dokumenty zaszumione online: e-maile, dzienniki czatów, wpisy w albumach, posty w grupach dyskusyjnych, wątki na forach dyskusyjnych, blogi itp. należą do tej kategorii. Ludzie zazwyczaj są mniej ostrożni w kwestii poprawności treści pisanych w takich nieformalnych trybach komunikacji. Charakteryzują się one częstymi błędami ortograficznymi, powszechnie i rzadko używanymi skrótami, niekompletnymi zdaniami, brakującymi znakami interpunkcyjnymi itd. Prawie zawsze hałaśliwe dokumenty są zrozumiałe dla człowieka, jeśli nie dla każdego, to przynajmniej dla zamierzonych czytelników.
SMS: Usługi krótkich wiadomości stają się coraz bardziej powszechne. Użycie języka w tekstach SMS znacznie różni się od standardowej formy języka. Dążenie do krótszej długości wiadomości ułatwiającej szybsze pisanie i potrzeba przejrzystości semantycznej kształtują strukturę tej niestandardowej formy znanej jako język tekstowy
Tekst generowany przez urządzenia ASR: ASR to proces konwersji sygnału mowy na sekwencję słów. System ASR przyjmuje sygnał mowy, taki jak monologi, dyskusje między ludźmi, rozmowy telefoniczne itp. jako dane wejściowe i generuje ciąg słów, zwykle nieoznaczonych znakami interpunkcyjnymi, jako transkrypty. System ASR składa się z modelu akustycznego, modelu językowego i algorytmu dekodującego. Model akustyczny jest trenowany na danych mowy i odpowiadających im transkryptach ręcznych. Model językowy jest trenowany na dużym korpusie jednojęzycznym. ASR konwertuje dźwięk na tekst, przeszukując przestrzeń modelu akustycznego i modelu języka za pomocą algorytmu dekodowania. Większość rozmów w centrach kontaktowych między agentami a klientami jest obecnie nagrywana. Aby przetworzyć te dane w celu uzyskania informacji o kliencie, konieczne jest przekonwertowanie dźwięku na tekst.
Tekst generowany przez urządzenia OCR: optyczne rozpoznawanie znaków, czyli "OCR", to technologia, która umożliwia przesyłanie cyfrowych obrazów tekstu pisanego na maszynie lub ręcznie do edytowalnego dokumentu tekstowego. Wykonuje zdjęcie tekstu i tłumaczy tekst na Unicode lub ASCII. . W przypadku optycznego rozpoznawania znaków pisanych ręcznie wskaźnik rozpoznawania wynosi od 80% do 90% przy czystym piśmie ręcznym.
Rejestry połączeń w centrach kontaktowych: Dzisiejsze centra kontaktowe (znane również jako centra telefoniczne, BPO, KPO) generują ogromne ilości niestrukturalnych danych w postaci rejestrów połączeń, oprócz wiadomości e-mail, transkrypcji połączeń, SMS-ów, transkrypcji czatów itp. Od agentów oczekuje się podsumowania interakcji zaraz po jej zakończeniu i przed podjęciem następnej. Ponieważ agenci pracują pod ogromną presją czasu, rejestry podsumowań są bardzo słabo napisane, a czasami nawet trudne do interpretacji przez człowieka. Analiza takich rejestrów połączeń jest ważna w celu zidentyfikowania obszarów problemowych, wydajności agentów, rozwijających się problemów itp.
Skupimy się na automatycznej klasyfikacji zaszumionego tekstu. Automatyczna klasyfikacja tekstu odnosi się do segregowania dokumentów na różne tematy w zależności od treści. Na przykład kategoryzowanie wiadomości e-mail klientów według tematów, takich jak problem z rozliczeniem, zmiana adresu, zapytanie o produkt itp. Ma ona ważne zastosowania w dziedzinie kategoryzacji wiadomości e-mail, tworzenia i utrzymywania katalogów internetowych, np. DMoz, filtr spamu, automatyczne kierowanie połączeń i wiadomości e-mail w centrum kontaktowym, filtr materiałów pornograficznych itp.

KATEGORIZACJA TEKSTU NOISY

Zadanie klasyfikacji tekstu jest jednym z modeli uczenia się dla danego zestawu klas i stosowania tych modeli do nowych niewidzianych dokumentów w celu przydzielenia klasy. Jest to ważny składnik wielu zadań ekstrakcji wiedzy; sortowanie wiadomości e-mail lub plików w czasie rzeczywistym do hierarchii folderów, identyfikacja tematów w celu obsługi operacji przetwarzania specyficznych dla tematu, wyszukiwanie strukturalne i/lub przeglądanie lub znajdowanie dokumentów odpowiadających długoterminowym stałym zainteresowaniom lub bardziej dynamicznym zainteresowaniom opartym na zadaniach. Dwa typy klasyfikatorów są powszechnie spotykane, tj. klasyfikatory statystyczne i klasyfikatory oparte na regułach. W technikach statystycznych model jest zazwyczaj trenowany na korpusie oznaczonych danych, a po przeszkoleniu system może być używany do automatycznego przypisywania niewidzianych danych. Przegląd klasyfikacji tekstu można znaleźć w pracy Aas & Eikvil. Biorąc pod uwagę zbiór dokumentów szkoleniowych D ={d₁, d₂, …, d_M} z prawdziwymi klasami {y₁, y₂,…, y_M}, zadaniem jest nauczenie się modelu. Ten model jest używany do kategoryzowania nowego nieoznaczonego dokumentu d_u. Zazwyczaj słowa pojawiające się w tekście są używane jako cechy. Inne aplikacje, w tym wyszukiwanie, w dużym stopniu polegają na uwzględnianiu znaczników lub struktury linków dokumentów, ale klasyfikatory zależą tylko od zawartości dokumentów lub zbioru słów obecnych w dokumentach. Po wyodrębnieniu cech z dokumentów każdy dokument jest konwertowany na wektor dokumentu. Dokumenty są reprezentowane w przestrzeni wektorowej; każdy wymiar tej przestrzeni reprezentuje pojedynczą cechę, a znaczenie tej cechy w tym dokumencie podaje dokładną odległość od początku. Najprostsza reprezentacja wektorów dokumentów wykorzystuje model zdarzeń binarnych, gdzie jeśli cecha j ∈ V pojawia się w dokumencie di, to j-ty składnik di wynosi 1, w przeciwnym wypadku wynosi 0. Jedną z najpopularniejszych technik klasyfikacji statystycznej jest naiwna metoda Bayesa. W metodzie naiwnej metody Bayesa prawdopodobieństwo przynależności dokumentu di do klasy c oblicza się następująco:



Ostateczne przybliżenie powyższego równania odnosi się do naiwnej części takiego modelu, tj. założenia niezależności słów, co oznacza, że cechy są uznawane za warunkowo niezależne, biorąc pod uwagę zmienną klasy. Systemy uczenia się oparte na regułach zostały przyjęte w problemie klasyfikacji dokumentów, ponieważ są bardzo atrakcyjne. Dobrze radzą sobie ze znajdowaniem prostych granic równoległych do osi. Typowy schemat klasyfikacji oparty na regułach dla kategorii, powiedzmy C, ma postać:

Przypisz kategorię C, jeśli poprzednik lub
Nie przypisuj kategorii C, jeśli poprzednik lub

Poprzednik w przesłance reguły zwykle obejmuje pewnego rodzaju porównanie wartości cech. Mówi się, że reguła obejmuje dokument lub dokument spełnia regułę, jeśli wszystkie porównania wartości cech w poprzedniku reguły są prawdziwe dla dokumentu. Jednym z dobrze znanych dzieł w domenie klasyfikacji tekstów opartej na regułach jest RIPPER. Podobnie jak standardowy algorytm "oddziel i zwyciężaj", buduje on zestaw reguł przyrostowo. Gdy reguła zostanie znaleziona, wszystkie dokumenty objęte regułą są odrzucane, w tym dokumenty pozytywne i negatywne. Reguła jest następnie dodawana do zestawu reguł. Pozostałe dokumenty są używane do tworzenia innych reguł w następnej iteracji. Zarówno w statystycznych, jak i opartych na regułach technikach klasyfikacji tekstu, treść tekstu jest jedynym wyznacznikiem kategorii, która ma zostać przypisana. Jednak szum w tekście zniekształca treść, a zatem czytelnicy mogą oczekiwać, że wydajność kategoryzacji zostanie obniżona przez szum w tekście. Klasyfikatory są zasadniczo szkolone w celu identyfikowania korelacji między wyodrębnionymi cechami (słowami) z różnymi kategoriami, które mogą być później wykorzystane do kategoryzacji nowych dokumentów. Na przykład słowa takie jak ekscytująca oferta otrzymaj darmowy laptop mogą mieć silniejszą korelację z kategoriami wiadomości e-mail spam niż wiadomości e-mail niebędące spamem. Szum w tekście zniekształca tę przestrzeń cech ekscytująca oferta otrzymaj darmowy laptop będzie nowym zestawem cech, a kategoryzator nie będzie w stanie powiązać go z kategorią wiadomości e-mail spam. Przestrzeń cech eksploduje, ponieważ ta sama cecha może pojawiać się w różnych formach z powodu błędów ortograficznych, słabego rozpoznawania, błędnej transkrypcji itp. W pozostałej części tej sekcji przedstawimy przegląd tego, jak ludzie podeszli do problemu kategoryzacji zaszumionego tekstu.

Kategoryzacja dokumentów OCRed

Elektronicznie rozpoznane dokumenty pisane ręcznie i dokumenty wygenerowane w procesie OCR są typowymi przykładami zaszumionego tekstu z powodu błędów wprowadzonych przez proces rozpoznawania. Vinciarelli zbadał charakterystykę szumu obecnego w takich danych i jego wpływ na dokładność kategoryzacji. Podzbiór dokumentów z zestawu danych klasyfikacji tekstów Reuters-21578 został wzięty i szum został wprowadzony przy użyciu dwóch metod: najpierw podzbiór dokumentów został ręcznie napisany i rozpoznany przy użyciu systemu rozpoznawania pisma ręcznego offline. W drugiej symulowano proces ekstrakcji oparty na OCR poprzez losową zmianę pewnego procentu znaków. Według nich, dla wartości przypomnienia do 60-70 procent, w zależności od źródeł, system kategoryzacji jest odporny na szum, nawet gdy współczynnik błędów terminów jest wyższy niż 40 procent. Zaobserwowano również, że wyniki z danych pisanych ręcznie wydają się być niższe niż te uzyskane z symulacji OCR. Zaproponowano ogólne systemy kategoryzacji tekstu oparte na analizie statystycznej reprezentatywnych korpusów tekstowych (Bayer i in., 1998). Cechy są ekstrahowane z tekstów szkoleniowych poprzez wybieranie podciągów z rzeczywistych form słów i stosowanie informacji statystycznych oraz ogólnej wiedzy językowej, a następnie redukcję wymiarowości poprzez transformację liniową. Rzeczywisty system kategoryzacji opiera się na podejściu najmniejszych kwadratów. System jest oceniany na podstawie zadań kategoryzacji streszczeń papierowych niemieckich raportów technicznych i listów biznesowych dotyczących skarg. Uzyskuje się około 80% dokładności klasyfikacji i widać, że system jest bardzo odporny na błędy rozpoznawania lub pisania. Problemy z kategoryzacją dokumentów OCR są również omawiane przez wielu innych autorów.

Kategoryzacja dokumentów ASRed
Automatyczne rozpoznawanie mowy (ASR) to po prostu proces konwersji sygnału akustycznego na sekwencję słów. Naukowcy zaproponowali różne techniki rozpoznawania mowy oparte na ukrytym modelu Markowa (HMM), sieciach neuronowych, dynamicznym odkształcaniu czasu (DTW). Wydajność systemu ASR jest zazwyczaj mierzona w kategoriach współczynnika błędów słów (WER), który jest pochodną odległości Levenshteina, działającej na poziomie słowa, a nie znaku. WER można obliczyć jako

WER = S + D + I / N gdzie S jest liczbą podstawień, D jest liczbą usunięć, I jest liczbą wstawek, a N jest liczbą słów w odniesieniu. Bahl i inni zbudowali system SR i zademonstrowali jego możliwości na zestawach danych testowych. Systemy ASR powodują podstawienia, usunięcia i wstawki słów, podczas gdy systemy OCR produkują zasadniczo podstawienia słów. Co więcej, systemy ASR są ograniczone przez leksykon i mogą dawać jako wynik tylko słowa należące do niego, podczas gdy systemy OCR mogą działać bez leksykonu (odpowiada to możliwości przepisania dowolnego ciągu znaków) i mogą generować sekwencje symboli niekoniecznie odpowiadające rzeczywistym słowom. Oczekuje się, że takie różnice będą miały silny wpływ na wydajność systemów zaprojektowanych do kategoryzacji dokumentów ASRed w porównaniu z kategoryzacją dokumentów OCRed. W przeszłości pojawiło się wiele prac nad automatyczną klasyfikacją typów połączeń w celu kategoryzowania połączeń, kierowania połączeń , uzyskiwania podsumowań dziennika połączeń , pomocy agentów i monitorowania. Tutaj połączenia są klasyfikowane na podstawie transkrypcji z systemu ASR. Jedna interesująca praca nad obserwacją wpływu szumu ASR na klasyfikację tekstu została wykonana na podzbiorze wzorcowego zestawu danych klasyfikacji tekstu Reuters-215782. Odczytali i automatycznie przepisali 200 dokumentów i zastosowali klasyfikator tekstu wytrenowany na czystym korpusie szkoleniowym Reuters-215783. Co zaskakujące, pomimo wysokiego poziomu szumu, nie zaobserwowali znacznego pogorszenia dokładności.

Wpływ błędów ortograficznych na kategoryzację

Błędy ortograficzne są integralną częścią tekstu pisanego - zarówno elektronicznego, jak i nieelektronicznego. Każdy czytelnik czytający tę książkę musiał zostać zrugany przez swojego nauczyciela w szkole za błędną pisownię słów! W tej erze tekstu elektronicznego ludzie stali się mniej ostrożni podczas pisania, co skutkuje źle napisanym tekstem zawierającym skróty, krótkie formy, akronimy, błędną pisownię. Takie elektroniczne dokumenty tekstowe, w tym e-maile, dzienniki czatów, posty, SMS-y, są czasami trudne do zinterpretowania nawet dla ludzi. Nie trzeba dodawać, że analiza tekstu na tak zaszumionych danych nie jest trywialnym zadaniem. Błędna pisownia może wpływać na wydajność automatycznej klasyfikacji na wiele sposobów, w zależności od charakteru stosowanej techniki klasyfikacji. W przypadku technik statystycznych różnice w pisowni zniekształcają przestrzeń cech. Jeśli zarówno trening, jak i korpus danych testowych są zaszumione, podczas nauki modelu klasyfikator będzie traktował warianty tych samych słów jako różne cechy. W rezultacie obserwowany rozkład prawdopodobieństwa łącznego będzie się różnił od rzeczywistego rozkładu. Jeśli proporcja błędnie napisanych słów jest wysoka, zniekształcenie może być znaczące i zaszkodzi dokładności wynikowego klasyfikatora. Jednak jeśli klasyfikator jest trenowany na czystym korpusie, a dokumenty testowe są zaszumione, błędnie napisane słowa będą traktowane jako niewidziane słowa i nie pomogą w klasyfikacji. W mało prawdopodobnej sytuacji błędnie napisane słowo obecne w dokumencie testowym może stać się inną prawidłową cechą, a co gorsza, może stać się prawidłową cechą wskazującą innej klasy. Standardową techniką w procesie klasyfikacji tekstu jest selekcja cech, która następuje po ekstrakcji cech i przed treningiem. Selekcja cech zazwyczaj wykorzystuje pewne środki statystyczne w korpusie treningowym i klasyfikuje cechy według ilości informacji (korelacji), które mają w odniesieniu do etykiet klas zadania klasyfikacji. Po uszeregowaniu zestawu cech, kilka najlepszych cech jest zachowywanych (zwykle rzędu setek lub kilku tysięcy), a pozostałe są odrzucane. Wybór cech powinien być w stanie wyeliminować błędnie napisane słowa obecne w dostarczonych danych treningowych (i) proporcja błędnie napisanych słów nie jest bardzo duża i (ii) nie ma regularnego wzorca błędów ortograficznych. Jednak zaobserwowano, że nawet przy wysokim stopniu błędów ortograficznych dokładność klasyfikacji nie cierpi zbytnio (Agarwal i in., 2007). Techniki klasyfikacji oparte na regułach są również negatywnie dotknięte błędami ortograficznymi. Jeśli dane treningowe zawierają błędy ortograficzne, niektóre z reguł mogą nie uzyskać wymaganego znaczenia statystycznego. Z powodu błędów ortograficznych obecnych w danych testowych prawidłowa reguła może nie zostać uruchomiona, a co gorsza, nieprawidłowa reguła może zostać uruchomiona, co doprowadzi do błędnej kategoryzacji. Załóżmy, że RIPPER nauczył się zestawu reguł takiego jak:

Przypisz kategorię "sporty", IF
(dokument zawiera {\it sporty}) OR
(dokument zawiera {\it ćwiczenia} AND {\it zajęcia na świeżym powietrzu})
OR
(dokument zawiera {\it ćwiczenia}, ale nie {\it praca domowa}
{\it egzamin}) OR
(dokument zawiera {\it gra} AND {\it zasada}) OR
…

Hipotetyczny dokument testowy zawierający powtarzające się wystąpienia słowa ćwiczenia, ale za każdym razem błędnie napisane jako exarcise, nie zostanie sklasyfikowany w kategorii sportów, i w związku z tym doprowadzi do błędnej klasyfikacji.

WNIOSEK

Przyjrzeliśmy się analizie zaszumionego tekstu. Temat ten zyskuje na znaczeniu, ponieważ generowanych jest coraz więcej zaszumionych danych, które wymagają przetwarzania. W szczególności przyjrzeliśmy się technikom korygowania zaszumionego tekstu i klasyfikacji. Przedstawiliśmy przegląd istniejących technik w tej dziedzinie i pokazaliśmy, że chociaż jest to trudny problem, można go rozwiązać za pomocą kombinacji nowych i istniejących technik.

WSTĘP

Znaczenie aplikacji do eksploracji tekstu rośnie proporcjonalnie do wykładniczego wzrostu tekstu elektronicznego. Wraz ze wzrostem Internetu wiele innych źródeł tekstu elektronicznego stało się naprawdę popularnych. Wraz ze wzrostem penetracji Internetu, wiele form komunikacji i interakcji, takich jak e-mail, czat, grupy dyskusyjne, blogi, grupy dyskusyjne, skrawki itp., stało się coraz bardziej popularnych. Generują one codziennie ogromną ilość zaszumionych danych tekstowych. Oprócz nich, innymi dużymi uczestnikami puli elektronicznych dokumentów tekstowych są centra telefoniczne i organizacje zarządzania relacjami z klientami w formie dzienników połączeń, transkrypcji połączeń, zgłoszeń problemów, e-maili ze skargami itp., tekst elektroniczny generowany przez proces optycznego rozpoznawania znaków (OCR) z dokumentów pisanych ręcznie i drukowanych oraz tekst mobilny, taki jak usługa krótkich wiadomości tekstowych (SMS). Chociaż natura każdego z tych dokumentów jest inna, istnieje wspólny wątek między nimi wszystkimi - obecność szumu. Przykładem ekstrakcji informacji jest ekstrakcja przypadków fuzji korporacyjnych, bardziej formalnie MergerBetween(company1,company2,date), ze zdania w wiadomościach online, takiego jak: "Wczoraj nowojorska firma Foo Inc. ogłosiła przejęcie Bar Corp."Opinion(product1,good), z wpisu na blogu, takiego jak: "Absolutnie spodobała mi się faktura kołder SheetK." Na poziomie powierzchownym istnieją dwa sposoby ekstrakcji informacji z zaszumionego tekstu. Pierwszym z nich jest oczyszczenie tekstu poprzez usunięcie szumu, a następnie zastosowanie istniejących najnowocześniejszych technik ekstrakcji informacji. W tym tkwi znaczenie technik automatycznej korekty zaszumionego tekstu. W tym rozdziale najpierw przejrzymy niektóre prace w obszarze korekty zaszumionego tekstu. Drugim podejściem jest opracowanie technik ekstrakcji, które są odporne na szum. Później w tym rozdziale zobaczymy, jak zadanie ekstrakcji informacji jest dotknięte szumem.

KOREKTA TEKSTU Z HAŁASEM

Zanim przejdziemy do technik przetwarzania tekstu z hałasem, krótko przedstawimy metody korygowania tekstu z hałasem. Jedną z najczęstszych form szumu w tekście jest błędna pisownia. Kukich przedstawia kompleksowy przegląd technik wykrywania i korygowania błędów ortograficznych . Zgodnie z tym przeglądem, zazwyczaj występują trzy rodzaje błędów ortograficznych, tj. typograficzne, takie jak teh, speel, poznawcze, takie jak recieve, conspeeracy i fonetyczne, takie jak abiss, nacherly. Należy rozróżnić automatyczne wykrywanie takich błędów i automatyczne korygowanie tych błędów. To drugie jest znacznie trudniejszym problemem. Większość ostatnich prac w tej dziedzinie dotyczy automatycznego korygowania błędów ortograficznych. Golding i Roth zaproponowali połączenie wariantu Winnow, algorytmu mnożnikowej aktualizacji wagi i głosowania większością ważoną w celu kontekstowej korekty pisowni. Mangu i Brill wykazali, że mały zestaw zrozumiałych dla człowieka reguł jest bardziej znaczący niż duży zestaw niejasnych cech i wag. Hybrydowe metody przechwytujące kontekst za pomocą trigramów znaczników części mowy i metoda oparta na cechach zostały również zaproponowane do obsługi kontekstowej korekty pisowni . Istnieje wiele prac związanych z automatyczną korektą błędów pisowni. Pełną bibliografię wszystkich prac związanych z wykrywaniem i korektą błędów pisowni można znaleźć w Beebe, 2005. W związku z tym, techniki automatycznej korekty błędów pisowni zostały zastosowane w innych aplikacjach, takich jak etykietowanie ról semantycznych. Istnieją również ostatnie prace nad korygowaniem wyników tekstu SMS , błędów OCR i błędów ASR

EKSTRAKCJA INFORMACJI Z SZUMNEGO TEKSTU

Celem ekstrakcji informacji (IE) jest automatyczne wyodrębnianie ustrukturyzowanych informacji z nieustrukturyzowanych dokumentów. Wyekstrahowane ustrukturyzowane informacje muszą być kontekstowo i semantycznie dobrze zdefiniowanymi danymi z danej domeny. Typowym zastosowaniem IE jest skanowanie zestawu dokumentów napisanych w języku naturalnym i wypełnianie bazy danych wyodrębnionymi informacjami. Konferencja MUC (Message Understanding Conference) była jedną z prób skodyfikowania zadania IE i jego rozszerzenia . Istnieją dwa podstawowe podejścia do projektowania systemów IE. Jedno obejmuje podejście inżynierii wiedzy, w którym ekspert domeny pisze zestaw reguł w celu wyodrębnienia poszukiwanych informacji. Zazwyczaj proces tworzenia systemu jest iteracyjny, w którym zestaw reguł jest pisany, system jest uruchamiany, a dane wyjściowe badane w celu sprawdzenia, jak system działa. Następnie ekspert domeny modyfikuje reguły, aby przezwyciężyć wszelkie niedostateczne lub nadmierne generowanie danych wyjściowych. Drugim jest podejście automatycznego szkolenia. To podejście jest podobne do klasyfikacji, w którym teksty są odpowiednio adnotowane za pomocą wyodrębnianych informacji. Na przykład, jeśli chcielibyśmy zbudować ekstraktor nazw miast, wówczas zestaw szkoleniowy zawierałby dokumenty ze wszystkimi oznaczonymi nazwami miast. System IE byłby szkolony na tym korpusie adnotacji, aby nauczyć się wzorców, które pomogłyby w wyodrębnianiu niezbędnych jednostek. System ekstrakcji informacji zazwyczaj składa się z kroków przetwarzania języka naturalnego, takich jak przetwarzanie morfologiczne, przetwarzanie leksykalne i analiza składniowa. Należą do nich stemming (redukcja odmienionych form wyrazów do ich tematu), tagowanie części mowy (przypisywanie każdemu wyrazowi etykiet, takich jak rzeczownik, czasownik itd.), a także analiza składniowa (analiza składniowa) służąca określeniu struktury gramatycznej zdań.

Adnotacja nazwanych jednostek w postach internetowych

Ekstrakcja nazwanych jednostek jest kluczowym zadaniem IE. Ma ona na celu zlokalizowanie i sklasyfikowanie atomowych elementów w tekście do wstępnie zdefiniowanych kategorii, takich jak nazwiska osób, organizacji, lokalizacji, wyrażenia czasu, ilości, wartości pieniężne, procenty itp. Systemy rozpoznawania jednostek wykorzystują techniki oparte na regułach lub modele statystyczne. Zazwyczaj parser lub tagger części mowy identyfikuje elementy, takie jak rzeczowniki, frazy rzeczownikowe lub zaimki. Te elementy wraz z formami powierzchniowymi tekstu są używane do definiowania szablonów do ekstrakcji nazwanych jednostek. Na przykład, aby oznaczyć nazwy firm, pożądane byłoby przyjrzenie się frazom rzeczownikowym, które zawierają w sobie słowa firma lub włączone. Reguły te można nauczyć się automatycznie przy użyciu oznaczonego korpusu lub można je zdefiniować ręcznie. Większość znanych podejść wykonuje to w czystym, dobrze sformatowanym tekście. Jednak adnotacja nazwanych jednostek w postach internetowych, takich jak ogłoszenia online, oferty produktów itp., jest trudniejsza, ponieważ te teksty nie są gramatyczne ani dobrze napisane. W takich przypadkach zestawy referencyjne były używane do adnotacji części postów. Zestaw referencyjny jest uważany za relacyjny zestaw danych ze zdefiniowanym schematem i spójnymi wartościami atrybutów. Posty są teraz dopasowywane do ich najbliższych rekordów w zestawie referencyjnym. W domenie biologicznej adnotacja nazwy genu, nawet jeśli jest wykonywana w dobrze napisanych artykułach naukowych, może być postrzegana w kontekście szumu, ponieważ wiele nazw genów pokrywa się z powszechnymi angielskimi słowami lub terminami biomedycznymi. Przeprowadzono badania nad wydajnością adnotatora nazwy genu po przeszkoleniu na zaszumionych danych .

Ekstrakcja informacji z dokumentów OCR

Dokumenty uzyskane z OCR mogą zawierać nie tylko nieznane słowa i słowa złożone, ale także niepoprawne słowa z powodu błędów OCR. W swojej pracy Miller i inni zmierzyli wpływ szumu OCR na wydajność IE. Wiele metod IE działa bezpośrednio na obrazie dokumentu, aby uniknąć błędów wynikających z konwersji na tekst. Przyjmują dopasowywanie słów kluczowych poprzez wyszukiwanie wzorców ciągów, a następnie używają globalnych modeli dokumentów składających się z modeli słów kluczowych i ich logicznych relacji, aby osiągnąć solidność dopasowania. Obecność błędów OCR ma szkodliwy wpływ na dostęp do informacji z tych dokumentów. Jednak przetwarzanie końcowe tych dokumentów w celu skorygowania tych błędów istnieje i wykazano, że daje duże ulepszenia.

Ekstrakcja informacji z dokumentów ASRed

Dane wyjściowe systemu ASR nie zawierają informacji o wielkości liter ani znaków interpunkcyjnych. Wykazano, że w przypadku braku znaków interpunkcyjnych ekstrakcja różnych jednostek składniowych, takich jak części mowy i frazy rzeczownikowe, nie jest dokładna (Nasukawa i in., 2007). Dlatego IE z dokumentów ASRed staje się trudniejsze. Miller i inni pokazali, jak wydajność IE zmienia się wraz z szumem ASR. Wykazano, że możliwe jest budowanie modeli zagregowanych z danych ASR . W tej pracy modele tematyczne są konstruowane przy użyciu redundancji międzydokumentowej w celu pokonania szumu. W tej pracy wykorzystano tylko kilka kroków przetwarzania języka naturalnego. Frazy zostały zagregowane w zakłóconej kolekcji, aby uzyskać czysty tekst bazowy.

TRENDY PRZYSZŁOŚCI

Coraz więcej danych ze źródeł takich jak czaty, rozmowy, blogi, grupy dyskusyjne musi zostać wydobytych, aby uchwycić opinie, trendy, problemy i możliwości. Te formy komunikacji zachęcają do nieformalnego języka, który może być uważany za zakłócony z powodu błędów ortograficznych, błędów gramatycznych i nieformalnego stylu pisania. Firmy są zainteresowane wydobywaniem takich danych, aby obserwować preferencje klientów i poprawiać ich zadowolenie. Agenci online muszą być w stanie zrozumieć posty w sieci, aby podejmować działania i komunikować się z innymi agentami. Klienci są zainteresowani zestawionymi recenzjami produktów z postów w sieci innych użytkowników. Charakter zakłóconego tekstu uzasadnia wyjście poza tradycyjne techniki analizy tekstu. Istnieje potrzeba opracowania technik przetwarzania języka naturalnego, które są odporne na szum. Należy również opracować techniki, które w sposób jawny i dorozumiany poradzą sobie z szumem tekstowym.

WNIOSEK

Przyjrzeliśmy się ekstrakcji informacji z zaszumionego tekstu. Temat ten zyskuje na znaczeniu, ponieważ generowanych jest coraz więcej zaszumionych danych i trzeba z nich uzyskać przydatne informacje. Przedstawiliśmy przegląd istniejących technik ekstrakcji informacji. Przedstawiliśmy również niektóre przyszłe trendy w analityce zaszumionego tekstu.

WSTĘP

Badamy zastosowanie sztucznych sieci neuronowych (ANN) do klasyfikacji widm sygnałów echa uderzeniowego. W tym artykule przedstawiamy analizy sygnałów symulowanych, a druga część artykułu szczegółowo opisuje wyniki eksperymentów laboratoryjnych. Zestaw danych do tego badania składa się z widm sygnałów echa uderzeniowego dźwiękowego i ultradźwiękowego uzyskanych ze 100 modeli elementów skończonych 3D. Widma te, wraz z kategoryzacją materiałów na klasy jednorodne i wadliwe w zależności od rodzaju defektów materiałowych, zostały wykorzystane do opracowania nadzorowanych klasyfikatorów sieci neuronowych. Zaproponowano cztery poziomy złożoności do klasyfikacji materiałów jako: stan materiału, rodzaj defektu, orientacja defektu i wymiar defektu. Porównano wyniki uzyskane z sieci neuronowych wielowarstwowego perceptronu (MLP) i radialnej funkcji bazowej (RBF) z algorytmami liniowej analizy dyskryminacyjnej (LDA) i k-najbliższych sąsiadów (kNN) (Duda, Hart i Stork, 2000). Uzyskano odpowiednie wyniki dla LDA i RBF. Echo uderzeniowe to technika nieniszczącej oceny oparta na monitorowaniu ruchu powierzchni wynikającego z krótkotrwałego uderzenia mechanicznego. Jest szeroko stosowana w zastosowaniach konstrukcji betonowych w inżynierii lądowej. Przeanalizowano poprzeczne tryby rezonansowe w sygnałach echa uderzeniowego w elementach o różnych kształtach, takich jak belki kołowe i kwadratowe, belki z pustymi kanałami lub wypełnieniami cementowymi itp. Ponadto zbadano analizy częstotliwości przesunięcia częstotliwości podstawowej do niższych wartości w celu wykrycia pęknięć . Propagację fali echa uderzeniowego można analizować na podstawie zachowania przejściowego i stacjonarnego. Sygnał wzbudzenia (uderzenie) wytwarza krótki etap przejściowy, w którym pierwsze fale P (naprężenie normalne), S (naprężenie ścinające) i Rayleigha (powierzchniowe) docierają do czujników; następnie zjawisko propagacji fali staje się stacjonarne, a rozmaitość różnych mieszanek fal, w tym różne zmiany trybu propagacji fali S na falę P i odwrotnie, dociera do czujników. Wzory przemieszczeń kształtu fali w tym ostatnim etapie są znane jako tryby rezonansowe materiału. Widma sygnałów echa uderzeniowego dostarczają informacji do klasyfikacji na podstawie trybów rezonansowych badanych materiałów. Drzewo klasyfikacyjne przedstawione w tym artykule ma cztery poziomy od klas globalnych do szczegółowych, z maksymalnie 12 klasami na najniższym poziomie. Poziomy to: (i) Stan materiału: jednorodny, jedna wada, wiele wad, (ii) Rodzaj wady: jednorodny, otwór, pęknięcie, wiele wad, (iii) Orientacja wady: jednorodna, otwór w osi X lub osi Y, pęknięcie w płaszczyznach XY, ZY lub XZ, wiele wad, oraz (iv) Wymiar wady: jednorodny, przechodzący przez i przechodzący przez rodzaje otworów i pęknięć poziomu III, wiele wad.

KONTEKST

Zastosowania sieci neuronowych w testach echa uderzeniowego obejmują: wykrywanie wad płyt betonowych, łączenie widm symulacji numerycznych i sygnałów rzeczywistych w celu trenowania sieci , identyfikację jednostronnie działających pęknięć podwarstwy przy użyciu generowanych numerycznie przebiegów jako danych wejściowych sieci, klasyfikację płyt betonowych na pełne i wadliwe (zawierające pustkę lub rozwarstwienie), wykorzystanie cech treningowych wyodrębnionych z wielu powtórzeń eksperymentów echa uderzeniowego na trzech próbkach w celu sklasyfikowania ich w trzech klasach oraz przewidywanie płytkich głębokości pęknięć w nawierzchniach asfaltowych przy użyciu cech z rozległego zestawu danych sygnałów rzeczywistych. We wszystkich tych badaniach wykorzystano wielowarstwową sieć neuronową perceptronową i monosensoryczne systemy echa uderzeniowego. W niedawnej pracy klasyfikowaliśmy dane echa uderzeniowego przez sieci neuronowe, wykorzystując cechy czasowe i częstotliwościowe wyodrębnione z sygnałów, odkrywając, że lepsze cechy to cechy częstotliwościowe . Tak więc niniejsza praca koncentruje się na wykorzystaniu wyłącznie informacji widmowych sygnałów echa uderzeniowego. Widma te zawierają dużą ilość redundantnych informacji. Zastosowaliśmy analizę głównych składowych (PCA) do widm w celu kompresji i usuwania szumu. Proponowany problem klasyfikacji i wykorzystanie składowych PCA widm jako cech klasyfikacji to nowa propozycja w zastosowaniu sieci neuronowych do testowania echa uderzeniowego. Istnieją dowody na to, że pierwsze składowe PCA zachowują zasadniczo wszystkie przydatne informacje, a ta kompresja optymalnie usuwa szum i może być używana do identyfikacji nietypowych widm . Główne składowe reprezentują źródła wariancji w danych. Projekcja p-tego widma na k-tą główną składową jest znana jako współczynnik domieszki a_k,p. Najbardziej znaczące główne składowe zawierają te cechy, które są najsilniej skorelowane w wielu widmach. Wynika z tego, że szum (który z definicji nie jest skorelowany z żadnymi innymi cechami) będzie reprezentowany w mniej znaczących składnikach. Tak więc, zachowując tylko bardziej znaczące składniki do reprezentowania widm, osiągamy kompresję danych, która preferencyjnie usuwa szum. Zredukowana rekonstrukcja, y_p p-tego widma x_p, jest uzyskiwana przez użycie tylko pierwszych r głównych składowych do rekonstrukcji widma, tj.



gdzie jest średnim widmem, które jest odejmowane od widm przed obliczeniem wektorów własnych, a u_k jest k-tą główną składową. x można uważać za zerowy wektor własny, chociaż stopień wariancji, który wyjaśnia, zależy od konkretnego zestawu danych i może być znacznie mniejszy niż ten wyjaśniony przez pierwsze wektory własne. Niech ε_p będzie błędem poniesionym przy użyciu tej zredukowanej rekonstrukcji. Z definicji x_p = y_p + ε_p, więc



ROZPOZNAWANIE WZORÓW USZKODZEŃ W SYMULACJI WIDMA ECHA UDERZENIA

Symulowane sygnały pochodziły z pełnej analizy dynamicznej 100 modeli elementów skończonych 3D symulowanego materiału w kształcie prostopadłościanu o wymiarach 0,07x0,05x0,22 m. (szerokość, wysokość i długość) podpartych do jednej trzeciej i dwóch trzecich długości bloku (kierunek z). Na podstawie analizy przejściowej szacowana jest dynamiczna odpowiedź struktury materiału (zmienne w czasie przemieszczenia w strukturze) pod działaniem obciążenia przejściowego. Obciążenie przejściowe, tj. uderzenie młota, symulowano, stosując historię siła-czas półsinusoidy o okresie 64 μs jako równomierne obciążenie ciśnieniowe na dwa elementy w środku przedniej powierzchni modelu. Stałe materiału sprężystego dla symulowanego materiału wynosiły: gęstość 2700 kg/m³, moduł sprężystości 69500 Mpa i współczynnik Poissona 0,22. W modelach wykorzystano elementy o wymiarach około 0,01 m. Elementy te mogą dokładnie uchwycić odpowiedź częstotliwościową do 40 kHz. Przebiegi przemieszczenia powierzchni pobrano z wyników symulacji w 7 węzłach w różnych miejscach na powierzchni materiału. Sygnały składały się z 5000 próbek zarejestrowanych z częstotliwością próbkowania 100 kHz. Aby umożliwić porównanie symulacji z eksperymentami, obliczono drugą pochodną przemieszczenia, aby działała z przyspieszeniami, ponieważ czujniki dostępne do eksperymentów były akcelerometry jednoosiowe. Przyspieszenia te mierzono w kierunku normalnym do płaszczyzny powierzchni materiału zgodnie z konfiguracją czujników. Ekstrakcja i selekcja cech. Badamy, czy zmiany w widmach, szczególnie w strefach częstotliwości podstawowych, są powiązane z kształtem, orientacją i wymiarem defektów. Informacje o widmach dla każdego kanału składają się z wartości n/2, co stanowi połowę liczby punktów użytych do obliczenia szybkiej transformaty Fouriera (FFT). Ze względu na zastosowaną konfigurację 7-kanałowego systemu echa uderzeniowego liczba danych dostępnych dla każdego testu echa uderzeniowego wynosiła 7^*n/2, np. dla FFT obliczonego z 256 punktami, 896 wartości byłoby dostępnych jako wpisy dla klasyfikatorów. Tak duża liczba wpisów mogłaby być nieodpowiednia dla etapu szkolenia sieci neuronowych. Biorąc pod uwagę redundancję widm sygnałów echa uderzeniowego, PCA zastosowano w dwóch krokach. W pierwszym kroku PCA zastosowano do widm każdego kanału jako metodę ekstrakcji cech. W drugim kroku PCA zastosowano do zestawu komponentów (widma skompresowane) uzyskanego w pierwszym kroku dla wszystkich kanałów i rejestrów jako metodę redukcji wymiarowości i selekcji cech. W ten sposób uzyskano skompresowany i reprezentatywny wzór widm dla wielokanałowej inspekcji echa uderzeniowego. Rozmiar zastosowanej FFT wynosił 1024 punkty, ponieważ użycie mniejszej liczby punktów nie było wystarczająco dobre do klasyfikacji. Po oszacowaniu widm dla wszystkich modeli, zostały one zgrupowane i znormalizowane według maksimum na kanał. Rozważono trzy opcje ustalenia liczby komponentów na pierwszym etapie PCA: wybranie liczby komponentów, które wyjaśniają minimum wariancji w danych, lub liczby komponentów, takich jak przyrost wariancji, lub stałej liczby komponentów. Pierwsze dwie opcje mogły oszacować zmienną liczbę komponentów na kanał i mogły wybrać więcej komponentów dla kanałów z "najgorszymi" sygnałami, tj. sygnałami o niskim stosunku sygnału do szumu (SNR), z powodu problemów z pomiarem (np. zły kontakt w czujniku interfejsu i materiale). W ten sposób wybieramy stałą liczbę składników = 20 na kanał, co wyjaśnia ponad 95% wariancji danych dla każdego z kanałów, więc całkowita liczba składników wynosiła 7*20=140 dla jednego modelu. Początkowe wpisy dla etapu klasyfikacji to 140 cech (składników widma) dla 100 modeli symulacyjnych. Do symulacji dodano 20 replik dla każdego modelu, które odpowiadały powtórzeniom wykonanym w eksperymentach. Repliki wygenerowano przy użyciu losowego szumu Gaussa z odchyleniem standardowym 0,1 oryginalnych sygnałów; następnie całkowita liczba rekordów dla symulacji wyniosła 2000 ze 140 składnikami widma. PCA zastosowano ponownie w celu zmniejszenia wymiarowości przestrzeni klasyfikacji i wybrania najlepszych cech widma do klasyfikacji. Po kilku wstępnych testach ustawiono 50 jako liczbę składników do klasyfikacji. Używając tej liczby składników, wyjaśniona wariancja wyniosła 98%. Po uzyskaniu 50 posortowanych komponentów zastosowano iteracyjny proces klasyfikacji zmieniający liczbę komponentów przy użyciu LDA i kNN jako klasyfikatorów. Krzywa opisana przez zbiór wartości błędu klasyfikacji i liczby komponentów (5, 10, 15,…, 50) ma punkt przegięcia, w którym informacje dostarczone dla komponentów zapewniają najlepszą klasyfikację. Po tym procesie selekcji cech uzyskano zredukowany zestaw cech ("lepszych" komponentów widm). Cechy te wykorzystano jako wpisy dla sieci neuronowych, co poprawiło wydajność klasyfikacji, zamiast wykorzystywać wszystkie komponenty widm. Liczba wybranych komponentów dla klasyfikacji sieci neuronowych wahała się od 20 do 30, w zależności od poziomu klasyfikacji (stan materiału, rodzaj wady, orientacja wady, wymiar wady). Klasyfikacja przebiegała zgodnie z metodą Leave-One-Out, unikając zapisów replik lub powtórzeń elementu testowego znajdujących się na etapie szkolenia tego elementu, więc wymuszono uogólnienie uczenia się wzorców. Tak więc niektóre rekordy użyte w szkoleniu i teście odpowiadały modelom lub okazom z tym samym rodzajem wady, ale zlokalizowanym w różnych pozycjach, a reszta rekordów odpowiadała innym rodzajom wadliwych elementów. Wyniki przedstawione w następnych sekcjach odnoszą się do średniego błędu na etapie testowania.

Wyniki symulacji

Najlepszy procent sukcesu klasyfikacji (75,9) uzyskano metodą LDA-kwadratową i LDA-Mahalanobis z 25 składnikami. Składniki te wybrano i wykorzystano jako dane wejściowe dla warstwy wejściowej sieci. Zastosowano jedną warstwę ukrytą (próbowano użyć różnej liczby neuronów, aby uzyskać najlepszą konfigurację liczby neuronów na tej warstwie), a liczba neuronów na warstwie wyjściowej została ustawiona jako liczba klas, w zależności od poziomu klasyfikacji. W klasyfikacjach z MLP zastosowano etap walidacji i metodę szkolenia odpornej propagacji. Parametr rozproszenia dostrojono do RBF. Najlepszą wydajność klasyfikacji uzyskano metodą LDA z odległością kwadratową, ale wyniki RBF są dość porównywalne. Ponieważ klasy nie są równie prawdopodobne na każdym poziomie, ogólne wyniki są ważone według prawdopodobieństwa klasy. Klasa jednorodna była całkowicie rozróżnialna, a klasa z wieloma defektami była najgorzej sklasyfikowana na każdym poziomie klasyfikacji. Procent sukcesu mógłby być znacznie wyższy poprzez zwiększenie sukcesu klasyfikacji dla klasy z wieloma defektami. Fakt ten wynikał z faktu, że modele z wieloma defektami składały się z modeli z różnymi pęknięciami i powodował zamieszanie między klasami pęknięć i wielu defektów. Procent sukcesu maleje w przypadku bardziej złożonych klasyfikacji, przy czym najniższa wydajność RBF wynosi 69% dla 12 klas

TRENDY PRZYSZŁOŚCI

Proponowaną metodologię przetestowano przy użyciu określonego rodzaju materiału i defektów oraz konfiguracji testów wielokanałowych. Można ją było przetestować przy użyciu modeli i próbek różnych materiałów, rozmiarów, konfiguracji czujników i parametrów przetwarzania sygnału. Istnieje kilka technik i algorytmów klasyfikacji, które można zbadać w przypadku proponowanego problemu. Niedawno zaproponowano model niezależnej analizy składowych (ICA) dla echa uderzeniowego , a także nowe klasyfikatory oparte na mieszankach ICA , które obejmują kwestie takie jak półnadzór na etapie szkolenia. Wykorzystanie wcześniejszej wiedzy na etapie szkolenia jest krytyczne w celu uzyskania odpowiednich modeli dla różnych rodzajów klasyfikacji. Tego rodzaju techniki mogą dać lepsze zrozumienie tego, jak model zmian oznaczonych i oznaczonych danych jest uczony przez klasyfikator. Ponadto potrzebne są dalsze badania nad kształtem przestrzeni klasyfikacji (widma sygnałów echa uderzeniowego), prawdopodobieństwem wartości odstających i obszarem decyzyjnym klas dla proponowanego problemu.

WNIOSEK

Wykazujemy wykonalność wykorzystania sieci neuronowych do wyodrębniania wzorców różnych rodzajów defektów z widm sygnałów echa uderzeniowego w symulacjach. Zastosowana metodologia była bardzo ograniczona, ponieważ w masie istniał tylko jeden element dla defektu w określonej lokalizacji i nie był on w fazie szkolenia, więc klasyfikator musiał przypisać odpowiednią klasę ze wzorcami elementów tej samej klasy w innych lokalizacjach. Wyniki można wykorzystać do wdrożenia proponowanej metody w rzeczywistych zastosowaniach oceny jakości materiałów; w tych zastosowaniach baza danych zebrana w rozsądnym czasie mogłaby zawierać próbki podobne do testowanego elementu, co ułatwiłoby proces klasyfikacji.

WSTĘP

Badamy zastosowanie sztucznych sieci neuronowych (ANN) do klasyfikacji widm sygnałów echa uderzeniowego. W tym artykule skupiamy się na analizach eksperymentalnych. Wyniki symulacji omówiono w artykule I. Echo uderzeniowe to procedura z Non-Destructive Evaluation, w której materiał jest wzbudzany uderzeniem młotka, co powoduje reakcję mikrostruktury materiału. Reakcja ta jest wykrywana przez zestaw przetworników umieszczonych na powierzchni materiału. Zmierzone sygnały zawierają rozpraszanie wsteczne z mikrostruktury ziarna i informacje o wadach badanego materiału. Zjawisko fizyczne echa uderzeniowego odpowiada propagacji fal w ciałach stałych. Gdy zakłócenie (naprężenie lub przemieszczenie) zostanie nagle przyłożone w punkcie na powierzchni ciała stałego, np. przez uderzenie, zakłócenie rozprzestrzenia się przez ciało stałe jako trzy różne typy fal naprężeń: fala P, fala S i fala R. Fala P jest związana z propagacją naprężenia normalnego, a fala S jest związana z naprężeniem ścinającym, oba rozprzestrzeniają się w ciele stałym wzdłuż sferycznych frontów fal. Ponadto fala powierzchniowa lub fala Rayleigha (fala R) przemieszcza się przez kołowy front fali wzdłuż powierzchni materiału. Po okresie przejściowym, w którym pojawiają się pierwsze fale, propagacja fali staje się stacjonarna w trybach rezonansowych materiału, które zmieniają się w zależności od defektów wewnątrz materiału. W materiałach wadliwych propagowane fale muszą otaczać defekty, a ich energia maleje, a wielokrotne odbicia i dyfrakcja z granicami defektów stają się falami odbitymi. W zależności od czasu obserwacji i częstotliwości próbkowania użytej w eksperymentach możemy być zainteresowani analizą etapu przejściowego lub stacjonarnego propagacji fali w testach echa uderzeniowego. Zwykle z wysoką rozdzielczością w czasie, analizy prędkości propagacji fal mogą dostarczyć użytecznych informacji, na przykład do zbudowania tomografii materiału badanego z różnych lokalizacji. Biorąc pod uwagę częstotliwość próbkowania, której użyliśmy w eksperymentach (100 kHz), cecha wyodrębniona z sygnału jako prędkość propagacji fal nie jest wystarczająco dokładna, aby odróżnić materiały jednorodne od różnych rodzajów wadliwych materiałów. Zestaw danych do tego badania składa się z widm sygnału echa uderzeniowego i ultradźwiękowego (1-27 kHz) uzyskanych z 84 równoległościennych (7x5x22cm. szerokości, wysokości i długości) próbek laboratoryjnych stopu aluminium serii 2000. Widma te, wraz z kategoryzacją jakości materiałów wśród klas jednorodnych, z jedną wadą i wieloma wadami, zostały wykorzystane do opracowania nadzorowanych klasyfikatorów sieci neuronowych. Wykazaliśmy, że sieci neuronowe dają dobre klasyfikacje (błąd <15%) materiałów na czterech poziomach szczegółowości klasyfikacji, takich jak stan materiału, rodzaj wady, orientacja wady i wymiar wady. Przedstawiono wyniki dla sieci neuronowych wielowarstwowego perceptronu (MLP) i radialnej funkcji bazowej (RBF), liniowej analizy dyskryminacyjnej (LDA) i algorytmów k-najbliższych sąsiadów (kNN)

TŁO

Zjawisko propagacji fal objętościowych w impakcie-eko można modelować za pomocą następujących dwóch równań



gdzie :

ρ₀ : Gęstość materiału
u_i : Wydłużenie długości względem punktu początkowego w kierunku siły.
∂T_ij/∂x_j : Zmiana siły w kierunku i na skutek odkształceń w kierunkach j.
c_ijkl : Tensor stałej sprężystości (prawo Hooke′a).
S_kl : Odkształcenie lub zmiana względnej objętości pod wpływem odkształcenia na powierzchni l w kierunku k w sześcianie unitarnym reprezentującym element materialny

Tak więc zmiana siły w kierunku i z powodu naprężeń powierzchniowych w kierunkach j elementarnego sześcianu materiału jest równa masie na objętość (gęstości) pomnożonej przez przyspieszenie odkształcenia (trzecie prawo Newtona w postaci tensorowej). Wyprowadzenie analitycznego rozwiązania problemów obejmujących propagację fali naprężeń w ograniczonych ciałach stałych jest bardzo skomplikowane, więc bibliografia na ten temat nie jest zbyt obszerna. Modele numeryczne, takie jak Metoda Elementów Skończonych (MES), można wykorzystać do uzyskania przybliżenia teoretycznej odpowiedzi materiału (Abraham O, Leonard C., Cote P. i Piwakowski B., 2000). Istnieje kilka badań, w których wykorzystano sygnały echa uderzeniowego w dziedzinie częstotliwości do wykrywania istnienia defektów w materiałach . Wykazano, że w widmach pojawia się sekwencja tonów i harmonicznych, są to podstawowe mody propagacji, które przemieszczają się wewnątrz materiału (materiał w kształcie bloku), a ich częstotliwości zależą od kształtu i rozmiaru materiału badanego przez echo uderzeniowe. W zależności od powierzchni bloku, na której znajduje się czujnik, wychwytywane są niektóre lub inne mody podstawowe. Jednak inne tony powstają w wyniku odbić fal z defektami w materiale, a ich częstotliwości są związane z głębokością wad. Ponadto obecność defektów powoduje przesunięcie częstotliwości modów podstawowych z powodu dyfrakcji. Sieć neuronowa MLP została zastosowana do echa uderzeniowego w konfiguracjach mono-sensorowych (używając tylko jednego akcelerometru) w celu wykrywania wad na płytach betonowych, identyfikacji jednostronnie działających pęknięć podwarstwy , klasyfikacji płyt betonowych na pełne i wadliwe . Te aplikacje wykorzystywały kilka eksperymentów i wiele powtórzeń lub łączono symulacje z sygnałami eksperymentalnymi, więc ich wyniki można zweryfikować z powodu prawdopodobnego nadmiernego dopasowania. Innym zastosowaniem jest przewidywanie płytkich głębokości pęknięć w nawierzchniach asfaltowych przy użyciu cech z rozległego zestawu danych sygnałów rzeczywistych. Niedawno dostarczyliśmy zastosowanie MLP, RBF i LVQ do drzewa klasyfikacyjnego zaproponowanego tutaj przy użyciu cech czasowych i częstotliwościowych wyodrębnionych z sygnałów, odkrywając, że lepsze cechy to cechy częstotliwościowe . W tym artykule demonstrujemy przydatność zastosowania PCA na widmach sygnałów echa uderzeniowego w celu uzyskania złożonych klasyfikacji w rzeczywistych eksperymentach. Pierwsze składniki PCA zachowują zasadniczo wszystkie przydatne informacje, a ta kompresja optymalnie usuwa szum. Główne składniki reprezentują źródła wariancji w danych. Tak więc najważniejsze główne składniki widm pokazują te cechy, które najbardziej różnią się między widmami: ważne jest, aby zdać sobie sprawę, że główne składniki nie reprezentują po prostu silnych cech. Głównymi składnikami są wektory własne macierzy symetrycznej; są to proste obroty w przestrzeni danych N-wymiarowej oryginalnych osi, na których zdefiniowano widma, dlatego przypominają widma.

ROZPOZNAWANIE WZORÓW DEFEKTU W EKSPERYMENTACH Z WIDMA ECHA UDERZENIA

Sygnały echa uderzenia

Sprzęt użyty w eksperymentach składał się z: młotka z instrumentami 084A14 PCB, 7 monoakcelerometrów 353B17 PCB, modułu akwizycji danych NI 6067E, kondycjonera sygnału ICP F482A18 i notebooka do przetwarzania i sterowania sygnałem. Częstotliwość próbkowania w akwizycji sygnału wynosiła 100 000 kHz, a zarejestrowany czas obserwacji wynosił 30 ms.



Rysunek a przedstawia fotografię sprzętu użytego w eksperymentach, należy zauważyć, że testowany jest okaz o wymiarach 7x5x22 cm z umieszczonymi czujnikami. Rysunek b przedstawia układ lokalizacji czujników na powierzchni elementu (1 czujnik na tylnej powierzchni, 4 czujniki na bocznych powierzchniach i 2 czujniki na górnej powierzchni), podpór i miejsca uderzenia. Czujniki S4, S6, S8 znajdują się w jednej trzeciej, a S3, S5, S7 w dwóch trzecich długości części w osi Z. S2 znajdują się w środku przeciwległej ściany do uderzenia. Wady składały się z otworów w kształcie cylindrów o średnicy 10 mm i pęknięć w kształcie równoległościanów o średnicy 5 mm o różnych orientacjach przez osie (X, Y) i płaszczyzny (XY, ZY, XZ) bloku materiału. Wymiary wad były dwa: przechodzące i półprzechodzące. Rysunek b przedstawia schemat wady klasy "pęknięcia półprzechodzącego w otworze zorientowanego w płaszczyźnie ZY".

Ekstrakcja i selekcja cech

Metodologia stosowana do ekstrakcji cech, selekcji cech, redukcji wymiarowości i klasyfikacji w widmach sygnałów echa uderzeniowego została zastosowana w Dokumencie I. Po pozyskaniu sygnału zastosowano czteroetapową procedurę: ekstrakcję cech, redukcję wymiarowości, selekcję cech i klasyfikację za pomocą sieci neuronowych. Na etapie ekstrakcji cech zastosowano 1024-punktową FFT do zmierzonych sygnałów, a widma te skompresowano za pomocą PCA, wybierając pierwsze 20 składników na każdy kanał. Tak więc wpisy na etapie redukcji wymiarowości wynosiły 140 składników (7 kanałów x 20) dla 84 próbek laboratoryjnych. Dla każdego eksperymentu (próbki) wykonano około 22 powtórzeń, więc łączna liczba rekordów wynosiła 1881 dla eksperymentów, każdy z 140 składnikami widma. Na etapie redukcji wymiarowości PCA zredukowało 140 składników widma do 50 składników widma z 92% wyjaśnioną wariancją. Ta macierz 50 wybranych komponentów według rekordów z 1881 r. stanowiła dane wejściowe dla procesu selekcji cech, którego celem było znalezienie "najlepszej" liczby komponentów do klasyfikacji. Następnie zastosowano różne testy klasyfikacji przy użyciu LDA i kNN, zmieniając liczbę komponentów od 5 do 50 w krokach co 5. Komponenty odpowiadające najlepszemu procentowi sukcesu w klasyfikacji z kNN i LDA wybrano jako wpisy do etapu klasyfikacji z MLP i RBF. Liczba komponentów widmowych wahała się od 10 do 30 w zależności od poziomu klasyfikacji. Parametry jako rozproszenie dla RBF i liczba neuronów w ukrytej warstwie dla MLP zostały dostrojone w celu uzyskania najlepszego procentu sukcesu klasyfikacji ANN. Cała klasyfikacja wykorzystywała metodę Leave-One-Out. Powtórzenia części w testowaniu nie były używane na etapie szkolenia, aby uniknąć zapamiętywania części przez klasyfikator zamiast uogólniania wzorców. Tabela 1 przedstawia podsumowane wyniki dla wszystkich klasyfikatorów zastosowanych na różnych poziomach klasyfikacji, wyniki te odnoszą się do średniego błędu na etapie testowania.

Wyniki eksperymentów

Ogólne wyniki klasyfikacji dla eksperymentów pokazują, że RBF jest najlepszym klasyfikatorem, poprawiając swoją wydajność o blisko 20% w odniesieniu do wyników symulacji w artykule I na bardziej złożonym poziomie klasyfikacji (12 klas). Odsetek sukcesu klasyfikacji poprawił się dla każdej klasy na każdym poziomie, szczególnie dla klasy z wieloma defektami z 25% do 92,6% na pierwszym poziomie i 89,1% na czwartym poziomie. W eksperymentach próbki z wieloma defektami przygotowano łącząc pęknięcia i otwory, więc nie było dużego zamieszania z klasami z wieloma defektami i z jednym defektem. Rzeczywiste eksperymenty echa uderzeniowego obejmowały zmienne losowe w jego wykonaniu, takie jak siła wstrzykiwana w wzbudzeniu uderzeniowym i położenie czujników, które mogą się różnić w zależności od elementu, ponieważ są sterowane ręcznie. Zmienne te dają powtórzenia eksperymentów z odpowiadającymi im widmami sygnału, które oddzielają lepsze obszary klasy niż szum Gaussa używany do uzyskania replik sygnałów symulowanego modelu. Wyniki klasyfikacji eksperymentalnych potwierdzają wykonalność wykorzystania sieci neuronowych do rozpoznawania wzorców defektów w sygnałach echa uderzeniowego. Klasa jednorodna jest doskonale sklasyfikowana, a wszystkie pozostałe sześć klas jest dobrze sklasyfikowanych, z wyjątkiem klasy "dziura Y" (48,8% powodzenia). Ta klasa jest często mylona ze wszystkimi klasami pęknięć; może to być spowodowane tym, że geometria defektu nie pozwala na wytworzenie dostrzegalnego wzoru fali ze zjawisk fal propagacyjnych. Ponadto klasa wielu defektów jest czasami mylona z pęknięciami i otworem X. Wynika to z tego, że określone wzory jednego z defektów wewnątrz niektórych próbek z wieloma defektami są bardziej dominujące w widmach, powodując, że widma wielu defektów są podobne do widm pęknięć lub otworów Y.

TRENDY PRZYSZŁOŚCI

Problem oceny materiałów zdefiniował różne poziomy klasyfikacji w hierarchicznym zarysie z różnym rodzajem wglądu w jakość badanego materiału. Można rozważyć ponowne sformułowanie problemu, aby klasyfikować defekty według zakresów wielkości defektu, niezależnie od ich kształtu lub orientacji, ten rodzaj klasyfikacji jest bardzo przydatny w takich gałęziach przemysłu jak fabryki marmuru. Stosowalność proponowanej metodologii musi zostać potwierdzona poprzez zastosowanie jej do różnych materiałów. Sieć neuronowa RBF dała dobre wyniki dla wszystkich poziomów klasyfikacji, ale należy przetestować więcej algorytmów, biorąc pod uwagę wykonalność jej wdrożenia w aplikacji w czasie rzeczywistym i poprawę procentowego sukcesu klasyfikacji. Na przykład nowe algorytmy klasyfikacji wykorzystują zależności liniowe w danych i umożliwiają uczenie się półnadzorowane . Tego rodzaju procedura modelowania i uczenia może być odpowiednia do klasyfikacji materiałów testowanych przez impactecho. Etap szkolenia i procent nadzoru to kluczowe tematy w celu opracowania odpowiedniego modelu z danych do klasyfikacji. W związku z tym, w zależności od rodzaju wadliwych materiałów użytych w szkoleniu, lepiej dostosowany model do konkretnej klasyfikacji byłby zdefiniowany. Wówczas fuzja decyzji podjęta przez różne klasyfikatory mogłaby być bardziej odpowiednia niż decyzja podjęta przez jeden klasyfikator.

WNIOSEK

Wykazujemy wykonalność wykorzystania sieci neuronowych do wyodrębniania wzorców różnych rodzajów defektów z widm sygnałów echa uderzeniowego w eksperymentach laboratoryjnych. Ogólne wyniki zastosowanych sieci neuronowych pokazują, że RBF jest bardziej odpowiednią techniką dla problemu echa uderzeniowego nawet na złożonych poziomach klasyfikacji, rozróżniając do 12 klas materiałów jednorodnych, jedno- i wielo-wadliwych. Proponowana metodologia przyniosła zachęcające wyniki w kontrolowanych eksperymentach laboratoryjnych (te same wymiary próbek, materiał o dobrej propagacji fal i dobrze zdefiniowane defekty). Procedurę tę należy przetestować w przypadku przetwarzania rzeczywistych materiałów przemysłowych o różnych wymiarach, rodzajach defektów i mikrostrukturach, dla których widma sygnałów echa uderzeniowego definiują rozmyte obszary do klasyfikacji.

WSTĘP

Wykrywanie wad w produkcji ma ogromne znaczenie w optymalizacji procesów przemysłowych. W rzeczywistości przemysłowa inspekcja materiałów i produktów inżynieryjnych ma na celu wykrywanie, lokalizację i klasyfikację wad tak szybko i dokładnie, jak to możliwe, w celu poprawy jakości produkcji. W tej dziedzinie istotny obszar stanowi inspekcja wizualna. Obecnie zadanie to jest często wykonywane przez eksperta. Niemniej jednak tego rodzaju inspekcja może okazać się czasochłonna i mieć niską powtarzalność, ponieważ kryteria oceny mogą się różnić w zależności od operatora. Ponadto zmęczenie wzroku lub utrata koncentracji nieuchronnie prowadzą do przeoczenia defektów. Aby zmniejszyć obciążenie testerów i poprawić wykrywanie wadliwych produktów, ostatnio wielu badaczy zaangażowało się w rozwój systemów w automatycznej kontroli wizualnej (AVI) producentów. Te systemy ujawniają łatwo niezawodne z technicznego punktu widzenia i odpowiednio naśladują ekspertów w procesie oceny defektów , nawet jeśli wykrywanie defektów podczas kontroli wizualnej może stać się trudnym zadaniem. W rzeczywistości w procesach przemysłowych należy obsługiwać dużą ilość danych, a wady należą do dużej liczby klas z dynamicznymi populacjami defektów, ponieważ defekty mogą prezentować podobne cechy w różnych klasach i różne cechy międzyklasowe . Dlatego też konieczne jest, aby systemy kontroli wizualnej były w stanie dostosować się do dynamicznych warunków pracy. W tym celu miękkie techniki obliczeniowe oparte na wykorzystaniu sztucznych sieci neuronowych (ANN) zostały już zaproponowane w kilku różnych obszarach produkcji przemysłowej. W rzeczywistości sieci neuronowe są często wykorzystywane ze względu na ich zdolność do rozpoznawania szerokiego zakresu różnych defektów. Chociaż w wielu przypadkach są one odpowiednie, w innych przypadkach sieci neuronowe nie mogą reprezentować najbardziej odpowiedniego rozwiązania. W rzeczywistości projektowanie sieci neuronowych często wymaga ekstrakcji parametrów i cech, podczas etapu wstępnego przetwarzania, z odpowiedniego zestawu danych, w którym rozpoznano najwięcej możliwych defektów. Dlatego metody oparte na sieciach neuronowych mogą być czasochłonne w przypadku aplikacji inline, ponieważ takie wstępne kroki mogą ujawnić złożoność. Z tego powodu, gdy w procesie przemysłowym ograniczenia czasowe odgrywają ważną rolę, można zaproponować rozwiązanie sprzętowe wyżej wymienionych metod, ale tego rodzaju rozwiązanie wymaga dalszego wysiłku projektowego, którego można uniknąć, biorąc pod uwagę komórkowe sieci neuronowe (CNN). Sieci neuronowe komórkowe mają duży potencjał do przezwyciężenia tego problemu, w rzeczywistości ich implementacja sprzętowa i masowy paralelizm mogą zaspokoić pilne ograniczenia czasowe niektórych procesów przemysłowych, umożliwiając włączenie diagnostyki do procesu produkcyjnego. W ten sposób metoda wykrywania defektów mogłaby umożliwić pracę w czasie rzeczywistym zgodnie ze specyficznym procesem przemysłowym.

TŁO

Sieci neuronowe komórkowe składają się z jednostek przetwarzających C(i, j), które są rozmieszczone w siatce M×N, jak pokazano na rysunku 1. Ogólna podstawowa jednostka C(i, j) nazywana jest komórką: odpowiada ona obwodowi nieliniowemu pierwszego rzędu, elektrycznie połączonemu z komórkami, które należą do zbioru Sr(i, j), zwanego sferą wpływu o promieniu r C(i, j). Taki zbiór Sr(i, j) jest zdefiniowany jako:



Sieć neuronowa M×N jest definiowana przez prostokątną tablicę M×N komórek C(i, j) zlokalizowaną w położeniu (i, j), i = 1, 2, .., M, j = 1, 2, …, N. Każda komórka C(i, j) jest definiowana matematycznie przez następujące równania stanu i wyjścia:



gdzie x_ij ∈ R, y_ij ∈ R i z_ij ∈ R to stan, wyjście i próg komórki C(i, j), y_kl ∈ R, a u_kl ∈ R to wyjście i wejście komórki C(k, l), odpowiednio. A(i, j; k, l) i B(i, j; k, l) są nazywane operatorami synaptycznymi sprzężenia zwrotnego i wejścia i jednoznacznie identyfikują sieć. Przedstawiony model obwodu stanowi paradygmat sprzętowy, który umożliwia szybkie przetwarzanie sygnałów. Z tego powodu w przeszłości sieci CNN były uważane za użyteczne ramy do wykrywania defektów w zastosowaniach przemysłowych. Kolejno zaproponowano różne wkłady oparte na CNN, działające w czasie rzeczywistym i mające na celu wykrywanie defektów w dziedzinie przemysłowej Przeprowadzono nieniszczącą kontrolę części mechanicznych w produkcji przemysłowej w lotnictwie, definiując algorytm, który jest wdrażany całkowicie za pomocą CNN. Metody te wykazują skuteczność, ale wymagany jest złożony system akwizycji, aby dostarczyć informacji o defektach. CNN stanowią procesory rdzeniowe systemu, który realizuje automatyczną inspekcję laminatów metalowych, podczas gdy zaproponowano dwa algorytmy oparte na CNN w celu wykrywania plam i nieprawidłowości w zastosowaniu tekstylnym. W obu pracach gwarantowany jest czas rzeczywisty, ale w kryteria syntezy parametrów obwodu CNN mogą okazać się trudne do spełnienia, podczas gdy takie kryteria nie są zdefiniowane. W poniższej sekcji zaproponowano metodę opartą na CNN, która umożliwia przezwyciężenie większości wad, jakie pojawiają się w zgłoszonych podejściach.

AUTOMATYCZNA METODA WYKRYWANIA WAD

W tej sekcji zaproponowano automatyczną metodę wizualnej kontroli wad powierzchniowych wyrobów. Metodę tę zrealizowano za pomocą architektury opartej na sieci CNN, która zostanie dokładnie opisana w rozdziale towarzyszącym . Proponowane podejście składa się z trzech kroków. Pierwszy z nich realizuje etap wstępnego przetwarzania, który umożliwia identyfikację ewentualnych obszarów wadliwych; w drugim etapie przeprowadzane jest dopasowanie takiego wstępnie przetworzonego obrazu do obrazu referencyjnego; na koniec w trzecim kroku uzyskiwany jest wyjściowy obraz binarny, w którym reprezentowane są tylko wady. Proponowane rozwiązanie nie wymaga ani złożonego systemu akwizycji, ani ekstrakcji cech; w rzeczywistości obraz jest bezpośrednio przetwarzany, a parametry syntezy systemu są automatycznie oceniane na podstawie statystycznych właściwości obrazu. Ponadto proponowany system jest dobrze przystosowany do implementacji na pojedynczej płytce. Schemat przedstawiający proponowaną metodę przedstawiono na rysunku



Jak widać, składa się on z trzech modułów: modułu wstępnego przetwarzania, modułu dopasowywania obrazu i modułu wykrywania defektów. Obrazy wejściowe, nazwane O i R, są pozyskiwane za pomocą kamery, która generuje obrazy o 256 poziomach szarości, których wymiary wynoszą m × n. Obraz O przedstawia testowany wyrób lub jego część. Taki obraz zawiera obszar zainteresowania (ROI), czyli konkretny obszar obiektu, w którym mają zostać wykryte defekty. Obraz R stanowi obraz referencyjny, na którym przedstawiono produkt bez defektów (lub jego część). Taki obraz jest przechowywany w pamięci i pozyskiwany w trybie offline podczas fazy kalibracji systemu. Służy do wykrywania możliwych odchyleń spowodowanych obecnością wgnieceń, zarysowań lub pęknięć na obserwowanej powierzchni. Aby umożliwić dobre dopasowanie obrazu referencyjnego i obrazu testowanego, bloki wstępnego przetwarzania realizują wzmocnienie kontrastu, dostarczając obrazy OF i RF, które stanowią dane wejściowe dla kolejnego modułu dopasowywania obrazów. Celem tego bloku jest znalezienie minimalnej różnicy między dwoma obrazami OF i RF. W rzeczywistości podczas procesu produkcyjnego system akwizycji może dawać obrazy, w których produkcja jest przesunięta zgodnie z czterema kierunkami głównymi. Oznacza to, że różnica między OF i RF może prowadzić do wykrycia fałszywych defektów. Moduł dopasowywania obrazów minimalizuje takie efekty, szukając najlepszego dopasowania między obrazem do przetworzenia a obrazem referencyjnym. Kolejno obraz różnicowy D zasila moduł wykrywania defektów. Ta część ma na celu wykrycie obecności wad w produkcie testowanym i daje obraz wyjściowy zawierający tylko wady. Obraz wyjściowy umożliwia aktywację systemów alarmowych zdolnych do wykrywania obecności wad, ułatwiając to zadanie przemysłowe, w rzeczywistości może wspierać ekspertów w ich diagnozach. Szczegółowa implementacja każdego modułu zostanie zilustrowana w drugiej części tego artykułu.

PRZYSZŁE TRENDY

Aby dostarczyć jak najwięcej informacji dotyczących defektów wykrywanych przez proponowane podejście w procesach przemysłowych, należy zidentyfikować cechy wad. Z tego powodu przyszłe prace będą poświęcone ocenie różnych cech, takich jak wymiary defektów, rodzaj uszkodzenia i jego stopień. Ponadto zostaną zbadane zalety stosowania proponowanej metody w różnych dziedzinach przemysłu i opracowane zostaną techniki minimalizujące ewentualne błędne klasyfikacje w poszczególnych zastosowaniach.

WNIOSEK

Tu zaproponowano metodę opartą na CNN do wizualnej inspekcji wad powierzchniowych wyrobów. Podejście to składa się z trzech modułów: Moduł wstępnego przetwarzania dostarcza obrazy, w których kontrast jest wzmocniony. Moduł dopasowywania obrazów umożliwia kompensację ewentualnego braku dopasowania między testowanym wyrobem a systemem akwizycji. Wreszcie Moduł wykrywania defektów umożliwia wyodrębnienie obrazów, które zawierają wady wyrobów. Sugerowana metoda oferuje atrakcyjne zalety. Ujawnia ona ogólne, dlatego może być wprowadzona w różnych dziedzinach przemysłu, w których identyfikacja powierzchownych anomalii, takich jak wgniecenia, korozja lub plamy na wyrobach, jest podstawowym zadaniem. Ponadto, sugerowana metoda jest finalizowana do wdrożenia za pomocą architektury, w całości utworzonej przez Cellular Neural Networks, wykorzystującej potencjał, jaki ten rodzaj sieci oferuje w przetwarzaniu sygnałów. Dlatego proponowane podejście umożliwia automatyzację procesów diagnostyki w linii, zmniejszając obciążenie operatorów w zakresie identyfikacji wad produkcyjnych.

WSTĘP

Automatyczna kontrola wizualna zajmuje istotne miejsce w wykrywaniu wad produkcji przemysłowej. W tej dziedzinie podstawową rolę odgrywają metody wykrywania powierzchownych anomalii w produkcji. W szczególności zaproponowano kilka systemów w celu zmniejszenia obciążenia operatorów ludzkich, unikając niedogodności wynikających z subiektywności kryteriów oceny. Proponowane rozwiązania są wymagane, aby móc obsługiwać i przetwarzać dużą ilość danych. Z tego powodu zaproponowano metody oparte na sieciach neuronowych ze względu na ich zdolność do radzenia sobie z szerokim rozproszeniem danych. Ponadto w wielu przypadkach metody te muszą spełniać ograniczenia czasowe procesów przemysłowych, ponieważ konieczne jest włączenie diagnostyki do procesu produkcyjnego. W tym celu architektury oparte na sieciach neuronowych komórkowych (CNN) okazały się skuteczne w dziedzinie wykrywania defektów w czasie rzeczywistym, ze względu na fakt, że sieci te gwarantują implementację sprzętową i masowy paralelizm. Na podstawie tych rozważań podano metodę identyfikacji powierzchownych uszkodzeń i anomalii w produkcji. Metoda ta ma na celu wdrożenie za pomocą architektury całkowicie utworzonej przez sieci neuronowe komórkowe, których syntezę zilustrowano w niniejszej pracy. Sugerowane rozwiązanie okazuje się skuteczne w wykrywaniu defektów, jak pokazano na dwóch przypadkach testowych przeprowadzonych na pompie wtryskowej i próbce tkaniny.

KONTEKST

W towarzyszącym artykule zaproponowano podejście do wykrywania wad powierzchniowych u producentów: podejście to można podzielić na trzy moduły, nazwane odpowiednio modułem wstępnego przetwarzania, modułem dopasowywania obrazu i modułem wykrywania wad. Pierwszy z nich realizuje etap wstępnego przetwarzania, który umożliwia identyfikację ewentualnych obszarów wadliwych; w drugim etapie przeprowadzane jest dopasowanie między takim wstępnie przetworzonym obrazem a obrazem referencyjnym; na koniec w trzecim kroku uzyskiwany jest wyjściowy obraz binarny, w którym reprezentowane są tylko wady. Proponowane rozwiązanie nie wymaga ani złożonego systemu akwizycji, ani ekstrakcji cech; w rzeczywistości obraz jest bezpośrednio przetwarzany, a parametry syntezy sieci są automatycznie oceniane na podstawie statystycznych właściwości obrazu. Ponadto proponowany system jest dobrze przystosowany do implementacji na pojedynczej płytce.

ARCHITEKTURA DIAGNOSTYKI OPARTA NA CNN

Szczegółowa implementacja każdego modułu zostanie zilustrowana poniżej. Kolejno przedstawiono wyniki uzyskane poprzez przetestowanie sugerowanej architektury na dwóch rzeczywistych przypadkach i przedstawiono dyskusję na temat wyników numerycznych.

Moduł wstępnego przetwarzania

Wstępne przetwarzanie jest realizowane przez blok Fuzzy Contrast Enhancement. Blok ten składa się z Fuzzy Associative Memory (FAM), opracowanej jako etap wstępnego przetwarzania systemu opartego na CNN. Proponowany obwód umożliwia przekształcenie obrazów o 256 poziomach szarości w obrazy rozmyte, których kontrast jest wzmocniony, dzięki rozciągnięciu ich histogramów. W tym celu opracowano odpowiednią procedurę rozmycia, aby zdefiniować dwa podzbiory rozmycia odpowiednie do opisu semantycznej zawartości wzorców, takich jak obrazy obiektów przemysłowych, które można sklasyfikować jako należące do klasy Object/Tło. Analogicznie, domena wartości wyjściowych została scharakteryzowana za pomocą dwóch wyjściowych podzbiorów rozmytych zdefiniowanych jako Dark i Light. W szczególności reguły rozmyte, które zapewniają mapowanie z obrazów oryginalnych (O/R) na rozmyte (OF/RF), można wyrazić jako:

JEŻELI O(i, j) ∈ Obiekt WTEDY Z(i, j) ∈ Ciemny
JEŻELI O(i, j) ∈ Tło WTEDY Z(i, j) ∈ Jasny

gdzie O(i, j) i OF(i, j) oznaczają wartość poziomu szarości piksela (i, j)-tego w obrazie oryginalnym i rozmytym, odpowiednio. Jak pokazano , zgłoszone reguły rozmyte można zakodować w pojedynczym FAM. Następnie sieć neuronowa komórkowa jest syntetyzowana tak, aby zachowywała się jak skodyfikowany FAM, poprzez przyjęcie procedury syntezy , w której synteza pamięci opartej na CNN, która zawiera wyżej wymienione reguły rozmycia, jest dokładnie sformułowana. Kontrastowe obrazy przedstawiają rozciągnięty histogram. Oznacza to, że taka operacja minimalizuje efekty szumu obrazu, spowodowanego problemami środowiskowymi, takimi jak kurz lub brud obiektywów aparatu. Ponadto zmniejsza niepożądane informacje ze względu na połączenie nierównomierności oświetlenia w obrazie i faktury produkcji .

Moduł dopasowywania obrazów



Na rysunku przedstawiono schemat blokowy odpowiadający modułowi dopasowywania obrazów. Celem tego modułu jest znalezienie najlepszego dopasowania między obrazami uzyskanymi przez przetworzenie pozyskanego obrazu i obrazu odniesienia. W tym celu obraz OF jest przesuwany o jeden piksel w czterech kierunkach głównych (PÓŁNOC; POŁUDNIE, WSCHÓD i ZACHÓD), przy użyciu czterech niezmiennych w przestrzeni sieci CNN i uzyskiwanie obrazów O_FN, O_FS, O_FE i O_FW. Kolejno przełącznik S₁ zmienia swoją pozycję, wyłączając obraz O_F. Obraz odniesienia RF jest odejmowany od obrazów O_FN, O_FS, O_FE O_FW i O_F, a następnie obliczana jest liczba b_N, b_S, b_E, b_W i b₀ czarnych pikseli w wynikowych obrazach D_N, D_S, D_E, D_W i D₀. Obraz, który najlepiej pasuje do obrazu odniesienia, przedstawia maksymalną liczbę czarnych pikseli. Dlatego taka wartość steruje przełącznikiem S₂, który umożliwia sprzężenie zwrotne obrazu, który najlepiej pasuje do obrazu odniesienia. W ten sposób obraz, który przedstawia minimalną różnicę, staje się wejściem do kolejnego kroku obliczeniowego. Przetwarzanie jest powtarzane, aż D₀ przedstawi najlepsze dopasowanie. Gdy ten warunek zostanie spełniony, obliczany jest obraz różnicowy D między D₀ a R_F. Jak można zauważyć, operacje potrzebne do każdego przesunięcia kierunkowego mogą być wykonywane jednocześnie, co skraca czas obliczeniowy na każdym kroku.

Moduł wykrywania defektów

Trzecia część proponowanej architektury to moduł wykrywania defektów. Podsystem jest syntetyzowany w celu obliczenia wyjściowego obrazu binarnego F, w którym obecne są tylko defekty. Taki moduł składa się z sekwencji obwodu głosowania głównego, asocjacyjnej pamięci CNN do poprawy kontrastu i obwodu progowego. Odpowiednia implementacja oparta na CNN jest uzyskiwana przez rozważenie sieci niezmiennych w przestrzeni. Szczegółowo obwód Major Voting minimalizuje liczbę fałszywych wykryć spowodowanych obecnością szumu, uwypuklając wgniecenia lub wady, które prowadzą do zmiany współczynnika odbicia światła w oryginalnym obrazie. Wyjście bloku Major Voting DM zasila sieć CNN działającą jako pamięć asocjacyjna opisana w poprzedniej podsekcji modułu Preprocessing. Ta operacja dostarcza obraz wyjściowy DMF, którego histogram jest bimodalny. W tego rodzaju obrazie wybór progu, który uwydatnia wady, jest wykonalny. W rzeczywistości właściwa wartość jest podawana przez średnią trybów histogramu. Następnie obraz ten jest segmentowany za pomocą odpowiadającej niezmiennej w przestrzeni sieci CNN , uzyskując odpowiadający obraz binarny F. W ten sposób błędy odpowiadające nieprawidłowej identyfikacji wad są minimalizowane, ponieważ po segmentacji widoczne są tylko wady.

Przykłady numeryczne

Możliwości zaprojektowanej architektury opartej na CNN zostały zbadane na obrazach przedstawiających centralną część pomp wtryskowych zawierających obszar zainteresowania (ROI), czyli kołnierz, taki jak przedstawiono na rysunku (a), którego histogram pokazano na rysunku (b).



Jak widać, obraz ten przedstawia dwa wgniecenia po lewej stronie i na dole obserwowanego obszaru. Wgniecenia są spowodowane kolizjami, które mogą wystąpić, gdy pompy są przemieszczane między różnymi lokalizacjami produkcyjnymi na różnych etapach montażu. Ten obraz i obraz odniesienia są najpierw przetwarzane przez obwód oparty na dwóch (4×4)-komórkowych CNN opisanych w poprzedniej podsekcji. Na rysunkach 3(a-b) pokazano odpowiadający obraz wyjściowy uzyskany przez zsyntetyzowane CNN i jego histogram.



Można zauważyć, że kontrast jest znacznie wzmocniony, a histogram jest rozciągnięty. Na rysunku (a) przedstawiono wyjście D modułu Image Matching: szum impulsowy spowodowany przesunięciem lub niedoskonałym oświetleniem obrazu lub odbiciem spowodowanym zabrudzeniem jest nadal obecny na tym etapie.



Na koniec D przekazuje dane do modułu Defect Detection: na rysunkach (b) i (c) przedstawiono odpowiednio wyjście bloku Major Voting DM i ostateczny obraz F. Jak można zaobserwować na obrazie DM, efekty nieregularnego oświetlenia lub zmiany odbić spowodowane kurzem lub zabrudzeniem są zminimalizowane. Wyniki są zachęcające, w rzeczywistości zaprojektowany system komórkowy zapewnia obraz wyjściowy , na którym obszary produkcji z defektami są dobrze widoczne i wykrywane przez białe piksele. Wydajność proponowanego systemu została przetestowana za pomocą drugiego eksperymentu przeprowadzonego na próbce tkaniny. Ta dziedzina przemysłu została zbadana, ponieważ ograniczenia czasowe zautomatyzowanego systemu wykrywania defektów w przemyśle tekstylnym mają kluczowe znaczenie.

Na rysunku (a) przedstawiono uzyskany obraz tkaniny.



W tym przypadku cały obraz wyrobu pokrywa się z obszarem zainteresowania. Można zauważyć, że jasny pionowy cienki pasek znajduje się pośrodku obrazu. Odpowiada on brakującemu stemplowi. W przedstawionym przykładzie identyfikacja defektów stanowi nietrywialny problem. W rzeczywistości wytłoczone obszary mają zróżnicowane kształty geometryczne, które można przedstawić za pomocą dużej liczby różnych poziomów szarości. Wcześniej zgłoszona metoda została zastosowana do wykrywania tego rodzaju defektów, dając obraz, na którym przedstawiono jedyny defekt (cienki pasek), podobnie jak w przypadku testowym zgłaszającym wgniecenia pomp wtryskowych. Na Rysunku (b)-(c)-(d) pokazano odpowiednio odpowiednie wyjścia modułu Preprocessing, modułu Image Matching i modułu Defect Detection. Można zauważyć, że centralny defekt został skutecznie wyizolowany, nawet jeśli pewien procent obszarów do zidentyfikowania został pominięty. Wynika to z faktu, że gdy trzeba wykryć szczegóły, wymagany jest maksymalny kontrast. Niemniej jednak, gdy zwiększa się kontrast, histogram wynikowego obrazu jest podkreślany w kierunku skrajnych wartości poziomów szarości w stosunku do pozyskanego obrazu. Oznacza to, że z powodu zjawiska nasycenia następuje utrata informacji o szczegółach. Wreszcie, w obrazie wyjściowym małe białe obszary są błędnie klasyfikowane jako defekty. Problem ten wynika z przesunięcia produkcji względem systemu akwizycji. Moduł Image Matching minimalizuje skutki takiego problemu, ale nie może ich całkowicie usunąć, gdy występują mechaniczne odkształcenia produkcji, jak w przypadku branży tekstylnej. Jak pokazano na rysunku (d), oznacza to obecność wyników fałszywie dodatnich, co zostanie zbadane później.

PRZYSZŁE TRENDY

Jak można wywnioskować z obserwacji uzyskanych wyników numerycznych, przyszłe prace będą poświęcone bardziej szczegółowej analizie błędnych klasyfikacji. W szczególności fałszywe pozytywy można analizować za pomocą dalszych technik, które wiążą cechy możliwych wadliwych stref z tymi zawierającymi efektywne defekty zgodnie z ograniczeniami aplikacji. Na przykład w zgłoszonych przykładach numerycznych fałszywe pozytywy mają rozmiary geometryczne, które są pomijalne w porównaniu z obszarami ewentualnych wad. Dlatego kontrola wymiarów obszaru mogłaby umożliwić rozróżnienie dwóch rodzajów regionów.

WNIOSEK

W tym artykule zaproponowano architekturę opartą na CNN do wizualnej inspekcji wad powierzchniowych producentów. Architektura składa się z modułów, które są w całości realizowane przez dobrze ugruntowane sieci obwodów. Zgłoszone podejście projektowe oferuje pewne interesujące zalety. Proponowane rozwiązanie nie wymaga ani złożonego systemu akwizycji, ani ekstrakcji cech, w rzeczywistości obrazy są przetwarzane bezpośrednio, a parametry syntezy, takie jak progi segmentacji obrazu, są automatycznie oceniane na podstawie statystycznych właściwości obrazu. Co więcej, dzięki możliwej implementacji sprzętowej sieci CNN, powstały system może sprostać pilnym ograniczeniom czasowym związanym z wykrywaniem w trybie on-line niektórych przemysłowych procesów produkcyjnych, umożliwiając włączenie diagnostyki do etapów produkcji.