Sieci bayesowskie

Reprezentowanie prawdopodobieństw w sieciach

Wiele ludzkich rozumowań dotyczy zdań i wielkości niepewności. Nasze przekonania na temat wielu rzeczy jest tymczasowe (tj. mogą ulec zmianie) i kwalifikowane (to znaczy mają różne poziomy zaufania). Również systemy AI muszą być w stanie poradzić sobie z niepewnymi informacjami. Fakty, oświadczenia i zasady agenta AI należy jak najbardziej uznać za tymczasowe i kwalifikowane. W końcu niektóre informacje są dostarczane przez ludzi, a niektóre pochodzą z czujników o ograniczonej precyzji i niezawodności. Jednak większość wczesnych prac w AI ignorowała niepewny charakter wiedzy. W rzeczywistości Marvin Minsky zauważył, że zawierał zredagowany tom wczesnych dokumentów AI "brak wyraźnego użycia pojęć probabilistycznych". Jednak większość badaczy AI uznaje obecnie, że znaczna część wiedzy potrzebnej maszynom musi zostać skorygowana na podstawie wartości prawdopodobieństwa i że w związku z tym wnioskowanie z tą wiedzą można najodpowiedniej przeprowadzić za pomocą narzędzi teorii prawdopodobieństwa. Ale podobnie jak w przypadku logicznego rozumowania, rozumowanie probabilistyczne podlega starej nemezis AI, eksplozji kombinatorycznej. Załóżmy na przykład, że wiedza agenta składa się z zestawu zdań. Ze względu na możliwe współzależności zdań, dokładne rozumowanie probabilistyczne zależy od znajomości czegoś więcej niż tylko prawdopodobieństwa każdego z tych zdań indywidualnie. Zamiast tego zwykle wymagane są wartości prawdopodobieństwa dla różnych kombinacji zdań wziętych razem, zwane "wspólnymi prawdopodobieństwami"; prowadzi to, w ogólnym przypadku, do niepraktycznie dużych reprezentacji i trudnych obliczeń. Wcześniejsze systemy AI, które mogły radzić sobie z niepewnością, takie jak MYCIN i PROSPECTOR, wprowadzały uproszczone założenia w celu złagodzenia tych trudności reprezentacyjnych i obliczeniowych. Ponieważ jednak systemy te nie uwzględniały istotnych współzależności między swoimi przekonaniami, często dawały niewłaściwe wyniki z powodu takich rzeczy, jak przeliczanie dowodów. W latach 80. wynaleziono kilka nowych, potężnych metod (i zaimportowano z innych dziedzin), które lepiej radziły sobie z zależnościami. Metody te znacznie uprościły zarówno problemy reprezentacyjne, jak i obliczeniowe. Obejmują one przedstawianie niepewnych przekonań i ich zależności w formie graficznej forma, zwana "probabilistycznym modelem graficznym". Opiszę najważniejszą wersję takich modeli. Po pierwsze, aby zilustrować niektóre trudności związane z rozumowaniem niepewnych przekonań i tym, jak moglibyśmy sobie z nimi poradzić, spójrzmy na przykład obejmujący różne propozycje dotyczące silnika samochodowego. Oto niektóre z nich to rzeczy, które moglibyśmy powiedzieć o silniku i jego częściach:

P1: Rozrusznik działa prawidłowo.
P2: Rozrusznik obraca silnik, gdy rozrusznik jest włączony.
P3: Układ paliwowy jest w porządku.
P4: Samochód uruchamia się po włączeniu rozrusznika.

Te propozycje są w oczywisty sposób powiązane. Po pierwsze, P4 zależy od pozostałych trzech - smutne spostrzeżenie, że P4 jest fałszywe, z pewnością zmieniłoby nasze zdanie na temat pozostałych trzech. Co więcej, nie potrzeba mechanika samochodowego, aby wiedzieć, że P1 i P2 są powiązane. Pełny opis zależności tutaj zaangażowanych wymaga wykazu wszystkich możliwości, aby wszystko było w porządku i nie było w porządku, a istnieje szesnaście takich możliwości. Jeśli oznaczymy przeciwieństwo zdania, umieszczając przed nim znak negacji (¬), wówczas ¬P1 oznacza "Rozrusznik nie działa". Korzystając z tego zapisu, istnieje szesnaście możliwości

P1; P2; P3; P4;
P1; P2; P3; ¬P4;
P1; P2; ¬P3; P4;
P1; P2; ¬3; ¬P4;
P1; ¬P2; P3; P4;
P1; ¬P2; P3; ¬P4;
P1; ¬P2; ¬P3; P4;
P1; ¬P2; ¬P3; ¬P4;
¬P1; P2; P3; P4;
¬P1; P2; P3; ¬P4;
¬P1; P2; ¬P3; P4;
¬P1; P2; ¬P3; ¬P4;
¬P1; ¬P2; P3; P4;
¬P1; ¬P2; P3; ¬P4;
¬P1; ¬P2; ¬P3; P4;
i
¬P1; ¬P2; ¬P3; ¬P4:

Ekspert, który wie o silnikach i ich oczekiwanej niezawodności, byłby prawdopodobnie w stanie przypisać wartości prawdopodobieństwa każdemu z tych szesnastu "stanów", w których układ silnika mógłby się znaleźć. Na przykład ekspert może określić, że ogólne prawdopodobieństwo połączenia, że wszystko jest w porządku, oznaczone przez p (P1; P2; P3; P4), wynosi 0,999. Musiałby podać szesnaście takich liczb. (W rzeczywistości wystarczyłoby tylko piętnaście, ponieważ szesnaście musiałoby sumować się do jednego. Są to jedyne możliwe stany i tak musi być w jednym przypadku.) Znajomość tych wspólnych prawdopodobieństw umożliwiłaby daną osobę (posiadającą cierpliwość i umiejętności w teorii prawdopodobieństwa ), aby obliczyć pewne inne prawdopodobieństwa, takie jak prawdopodobieństwo, że samochód uruchomi się, biorąc pod uwagę, powiedzmy, że układ paliwowy jest zdecydowanie w porządku. Określenie piętnastu liczb dla tego małego przykładu nie wydaje się zbyt uciążliwe, ale dla bardziej realistycznego problemu, powiedzmy, że z trzydziestoma różnymi propozycjami, trzeba by podać 2³⁰ - 1 = 1 073,741,823 liczb. Co więcej, jeśli istnieją również wielkości, które mogą przyjmować kilka wartości (oprócz zdań, które są wartościowane binarnie), liczba możliwości rośnie jeszcze bardziej. Oczywiście przyjąłem tutaj najgorszy przypadek, mianowicie przypadek, w którym wszystkie cztery zdania mogą się od siebie w skomplikowany sposób zależeć. Na drugim biegunie jest przypadek, w którym zdania są całkowicie od siebie niezależne. Następnie każde z szesnastu prawdopodobieństw można obliczyć za pomocą wzorów takich jak p (P1; P2; P3; P4) = p (P1) p (P2) p (P3) p (P4) (ze znakami ¬ wstawionymi zgodnie z wymaganiami) i musielibyśmy jedynie określać prawdopodobieństwa dla każdej z czterech propozycji osobno. Mój przykład na temat silników samochodowych znajduje się pomiędzy tymi dwoma skrajnościami. Podobnie jest z wieloma znacznie większymi i bardziej realistycznymi problemami. Ta "pomiędzy" jest kluczem do uczynienia bardziej prawdopodobnym rozumowania probabilistycznego. Chociaż statystycy wcześniej rozpoznawali i wykorzystywali ten fakt, to Judea Pearl opracował niektóre z głównych metod reprezentacyjnych i obliczeniowych. Pearl, profesor informatyki na Uniwersytecie Kalifornijskim w Los Angeles, był zaskoczony kontrastem między, z jednej strony, łatwością, z jaką ludzie rozumują i wyciągają wnioski na podstawie niepewnych informacji, a z drugiej strony obliczeniami trudności w powielaniu tych umiejętności za pomocą obliczeń prawdopodobieństwa. Jak to później ujął, zaczął od następujących przypuszczeń:

1. Spójna zgodność między prawdopodobnym rozumowaniem [przez ludzi] a rachunkiem prawdopodobieństwa nie może być przypadkowa, ale zdecydowanie sugeruje, że ludzka intuicja przywołuje jakąś surową formę obliczeń probabilistycznych.
2. W świetle szybkości i skuteczności ludzkiego rozumowania, trudności obliczeniowe, które nękały wcześniejsze systemy probabilistyczne, nie mogą być bardzo fundamentalne i należy je przezwyciężyć, dokonując właściwego wyboru, upraszczając założenia, które ludzie przechowują w swojej głowie.

Kluczowym wkładem Pearl było przekonanie o propozycjach i innych wielkości często można uznać za "bezpośrednie przyczyny" innych przekonań i że te związki przyczynowe mogą być reprezentowane w strukturach graficznych, które kodują upraszczające założenia dotyczące zależności między prawdopodobieństwami. Oczywiście, Pearl nie była pierwszą, która sugerowała użycie struktur graficznych do kodowania probabilistycznego informacje. Sam wspomina o wcześniejszych pracach. Russell i Norvig napisali, że dzieło brytyjskiego statystyka I.J. Gooda można uznać za prekursora współczesnych sieci bayesowskich… ". A fizycy wskazują na ściśle powiązaną pracę Hansa A. Bethe. W przypadku naszego problemu z silnikiem samochodowym rodzaj wykresu, który może zastosować Pearl, pokazano poniżej



Każda interesująca propozycja jest reprezentowana przez "węzeł" na wykresie. Strzałki pokazują bezpośredni wpływ różnych zdań, a także wskazują między nimi na pewne probabilistyczne niezależności. Na przykład prawdopodobieństwo P4 (samochód uruchamia się po włączeniu rozrusznika) wcale nie zależy od prawdopodobieństwa P1 (silnik rozrusznika jest w porządku), jeśli już wiemy (podano) P2 (silnik rozrusznika obraca się silnik, gdy zapłonnik jest włączony) i P3 (układ paliwowy jest w porządku). Znajomość P1 nie mówi nam nic nowego o P4, jeśli znamy już P2 i P3. W języku teorii prawdopodobieństwa prawdopodobieństwo P4 jest warunkowo niezależne od P1, biorąc pod uwagę rodziców P4, a mianowicie P2 i P3. W rzeczywistych zadaniach wnioskowania istnieje wiele takich warunkowych niezależności, które można ujawnić za pomocą tego rodzaju grafów przyczynowych. Uwzględnienie ich znacznie zmniejsza złożoność probabilistycznego rozumowania. W naszym przykładzie silnika samochodowego zamiast piętnastu prawdopodobieństw, które byłyby potrzebne w ogólnym przypadku, teraz potrzebujemy tylko ośmiu. Są to: prawdopodobieństwo P4 dla P2 i P3 dla czterech różnych stanów P2 i P3:

p(P4 | P2; P3);
p(P4 | P2; ¬P3);
p(P4 | ¬P2; P3);
p(P4 | ¬P2; ¬P3);

prawdopodobieństwo P2 podane P1 dla dwóch różnych stanów P1, mianowicie p (P2 | P1) i p (P2 | ¬ P1); oraz prawdopodobieństwa P1 i P3, a mianowicie p (P1) i p (P3). Każdy z tych zestawów wartości prawdopodobieństwa jest przechowywany w tak zwanej "tabeli prawdopodobieństwa warunkowego" (CPT) powiązanej z odpowiadającym mu węzłem w sieci. (CPT węzła bez rodziców jest tylko bezwarunkowym prawdopodobieństwem dla tego węzła). Wykorzystując wynik z teorii prawdopodobieństwa można obliczyć szesnaście wspólnych prawdopodobieństw (wymaganych do dokładnego uzasadnienia probabilistycznego) z tych ośmiu. Tak naprawdę nie dostajemy tutaj czegoś za nic. Zamiast tego wykorzystujemy dodatkową wiedzę dostarczoną przez warunkowe niezależności uwidocznione przez sieć.

Ponieważ reguła Bayesa odgrywa znaczącą rolę w obliczaniu prawdopodobieństwa różnych węzłów, biorąc pod uwagę prawdopodobieństwa innych, Pearl ukuł frazę "Bayesowskie sieci przekonań" (zwykle upraszczane do sieciach bayesowskich lub sieci przekonań) dla tego rodzaju wykresów. Okazało się, że dość łatwe jest budowanie dużych sieci bayesowskich poprzez uważne stwierdzenie, które twierdzenia bezpośrednio wpływają ("powołują") na inne. Tak skonstruowane sieci są tym, co teoretycy grafów nazywają "ukierunkowanymi wykresami acyklicznymi" (DAG): "skierowanymi", ponieważ strzałki wskazują od węzłów przyczyny do spowodowanych węzłów, i "acykliczne", ponieważ podążanie za strzałkami na zewnątrz od węzła nigdy nie prowadzi z powrotem do tego samego węzła. Można by zapytać, skąd pochodzą wartości prawdopodobieństwa w CPT? W przypadku niektórych sieci być może specjalista obeznany z tym, w jaki sposób niektóre zdania wpływają na inne, może być w stanie zgadnąć o prawdopodobieństwach. Takie domysły nazywane są \ subiektywnymi prawdopodobieństwami ", ponieważ opierają się na subiektywnych wyobrażeniach eksperta o przyczynie i skutku. Jednak zdecydowanie najbardziej użyteczną metodą zapełniania CPT wartościami jest oszacowanie ich na podstawie dużej bazy danych rzeczywistych przypadków. Wyjaśnię, jak to się robi w następnej sekcji. Niezależnie od tego, w jaki sposób są uzyskane, CPT (wraz ze strukturą sieci) są wykorzystywane w obliczeniach dotyczących wpływu prawdopodobieństw na niektóre węzły w sieci innych. Obliczenia te nazywane są "wnioskowaniem probabilistycznym". Opracowano różne praktyczne metody obliczeniowe {nawet w przypadku dość dużych sieci potrzebnych do realistycznych problemów. Bez przeprowadzania jakichkolwiek rzeczywistych obliczeń wykorzystam sieć małych silników do zilustrowania trzech głównych style wnioskowania probabilistycznego w sieciach bayesowskich. Na przykład, jeśli na pewno wiedzieliśmy tylko, że silnik rozruchowy był w porządku [to znaczy p (P1) = 1)], moglibyśmy obliczyć prawdopodobieństwo że samochód się uruchomi. "Migracja" znanych wartości prawdopodobieństwa w dół w sieci (w kierunku strzałek) jest zwykle nazywana "rozumowaniem przyczynowym". I odwrotnie, gdybyśmy wiedzieli, że samochód się nie uruchomi [to znaczy p (P4) = 0], moglibyśmy obliczyć prawdopodobieństwo, że silnik rozrusznika jest sprawny, a układ paliwowy jest sprawny. Migracja wartości prawdopodobieństwa w górę w sieci (w kierunku przeciwnym do strzałek) jest zwykle nazywana rozumowaniem "dowodowym" lub "diagnostycznym". To właśnie robią lekarze (i inni rozwiązywacze problemów), gdy mają objaw i próbują wywnioskować prawdopodobieństwo przyczyn. Istnieje również inny ważny styl rozumowania, który nazywa się "wyjaśnianiem". Oto przykład: Załóżmy, że wiemy, że samochód się nie uruchamia, i wyliczyliśmy wartości prawdopodobieństwa dla układu paliwowego stanowiącego problem (to znaczy nie jest w porządku) i dla silnika rozruchowego stanowiącego problem. Potem okazało się, że w rzeczywistości silnik rozrusznika w rzeczywistości zawiódł. Biorąc pod uwagę te dodatkowe informacje, chcielibyśmy zmniejszyć prawdopodobieństwo wystąpienia problemu z układem paliwowym. Problem z rozrusznikiem silnika "wyjaśnia" fakt, że samochód nie chce się uruchomić, więc mamy mniej powodów, aby podejrzewać układ paliwowy. Fakt, że silnik rozruchowy nie uruchamia się, "wyjaśnia" możliwy problem z układem paliwowym. Strategia wyjaśniania jest powszechnie stosowana przez ludzi w medycynie, prawie, nauce i codziennym rozumowaniu. Na przykład obrońca może przytoczyć dowody na to, że inna osoba (nie jego klient) została zidentyfikowana na monitoringu telewizyjnym systemu bankowego , co tłumaczy zaangażowanie jego klienta w napad na bank. Zilustrowano efekt wyjaśniania za pomocą faktycznych obliczeń wnioskowania przeprowadzonych w nieco większej sieci dotyczącej silników



Po zaobserwowaniu, że samochód się nie uruchamia, prawdopodobieństwo, że problem stanowi rozrusznik silnik, wynosi 0,023 (przy użyciu tabel prawdopodobieństwa warunkowego sieci, których nie pokazano na schemacie), oraz prawdopodobieństwo, że układ paliwowy jest problem jest obliczany na 0,283. Ale po dodatkowym stwierdzeniu awarii silnika rozrusznika prawdopodobieństwo, że przyczyną problemu jest układ paliwowy, spada o ponad połowę do 0,1. Gdybyśmy chcieli zbudować sieć bayesowską o silniku samochodowym, który byłby bardziej realistyczny i użyteczny, musielibyśmy wspomnieć o wielu innych komponentach i podsystemach. Taka sieć może zawierać setki węzłów wraz z powiązanymi tabelami prawdopodobieństwa warunkowego. Mimo że warunkowe niezależności zmniejszyłyby liczbę indywidualnych prawdopodobieństw, które należy określić, ich liczba może być tak duża, że dokładne wnioskowania probabilistyczne nadal byłyby trudne do obliczenia obliczeniowego - przy założeniu, że wartości tych prawdopodobieństw mogłyby zostać nawet zebrane. Po zaobserwowaniu, że samochód się nie uruchamia, prawdopodobieństwo, że problem stanowi silnik rozrusznika, wynosi 0,023 (przy użyciu tabel prawdopodobieństwa warunkowego sieci, których nie pokazano na schemacie), oraz prawdopodobieństwo, że układ paliwowy jest problem jest obliczany na 0,283. Ale po dodatkowym stwierdzeniu awarii silnika rozrusznika prawdopodobieństwo, że przyczyną problemu jest układ paliwowy, spada o ponad połowę do 0,1. Gdybyśmy chcieli zbudować sieć bayesowską o silniku samochodowym, który byłby bardziej realistyczny i użyteczny, musielibyśmy wspomnieć o wielu innych komponentach i podsystemach. Taka sieć może zawierać setki węzłów wraz z powiązanymi tabelami prawdopodobieństwa warunkowego. Mimo że warunkowe niezależności zmniejszyłyby liczbę indywidualnych prawdopodobieństw, które należy określić, ich liczba może być tak duża, że dokładne wnioskowania probabilistyczne nadal byłyby trudne do obliczenia obliczeniowego - przy założeniu, że wartości tych prawdopodobieństw mogłyby zostać nawet zebrane. Na szczęście możliwe są różne uproszczenia, które pozwalają na dalsze zmniejszenie potrzebnej liczby prawdopodobieństw. Dzięki nim obliczenia przybliżonego, ale wciąż przydatnego wnioskowania w dużych sieciach stają się wykonalne. Warto wspomnieć, że niektóre z tych uproszczeń i przybliżone metody obliczeniowe wymagają dość złożonych narzędzi matematycznych, z których wiele pochodzi z sąsiednich pól, takich jak statystyka i inżynieria sterowania. Tego rodzaju obliczenia sieci bayesowskiej stanowią kolejny przykład tego, jak to zrobić problemy wcześniej uważane za nierozwiązywalne obliczeniowo doprowadziły do postępu technicznego. Na ryc. 28.4 pokazuję przykład dość dużej sieci bayesowskiej.



Sieć reprezentuje wiedzę na temat chorób wątroby i dróg żółciowych (wątroby, pęcherzyka żółciowego i pokrewnych narządów) i została opracowana jako narzędzie do stosowania wśród studentów medycyny. Ta sieć pochodzi częściowo z bazy wiedzy INTERNIST-1 (patrz str. 301). Ma 448 węzłów i 908 strzał. Gdyby zastosowano pełne tablice prawdopodobieństwa warunkowego, należałoby podać 133 931,430 prawdopodobieństw. Programiści sieci byli w stanie zmniejszyć tę liczbę do 8 254 wartości, korzystając z różnych uproszczeń. Sieci bayesowskie zawierające setki węzłów zostały wykorzystane do zastosowań w biologii, medycynie, klasyfikacji dokumentów, przetwarzaniu obrazów, prawie, dekodowaniu z korekcją błędów i wielu innych. Wiele z tych sieci pochodzi automatycznie z dużych zestawów danych, temat ten omówię w następnej sekcji.

Automatyczna konstrukcja sieci bayesowskich

Jednym z powodów, dla których sieci bayesowskie stały się tak ważne, jest to, że można je automatycznie konstruować z dużych baz danych. Oznacza to, że można się ich "nauczyć", a wyuczonych wersji można użyć do uzasadnienia danego tematu. Dwoma pionierami w rozwoju tych metod uczenia się byli Greg Cooper i Edward Herskovits. Temat jest nadal aktywnym obszarem badawczym, a kilku innych wniosło znaczący wkład. Oto, ogólnie rzecz biorąc, sposób działania tego procesu. Aby nauczyć się sieci, należy poznać jej strukturę, to znaczy rozmieszczenie jej węzłów i łączy, a także CPT sieci. Najpierw wyjaśnię, w jaki sposób można nauczyć się CPT dla znanej struktury, a następnie, w jaki sposób można nauczyć się samej struktury, mimo że te dwa procesy są ze sobą powiązane. Rozważmy jeszcze raz czterowęzłową sieć bayesowską dla silnika samochodowego. Jak możemy nauczyć się CPT dla węzła P4 (czyli Car Starts) - tego, którego rodzicami są P2 (czyli Car Cranks) i P3 (czyli układ paliwowy OK)? Używając moich skrótów dla tych zdań, że CPT składa się z następujących prawdopodobieństw warunkowych:

p(P4 | P2; P3);
p(P4 | P2; ¬P3);
p(P4 | ¬P2; P3);
i
p(P4 | ¬P2; ¬P3):

Gdybyśmy mieli duży zbiór próbek sytuacji, w których samochód czasami zacina się, a czasem nie, w którym samochód czasami kręci się, a czasem nie, a czasami układ paliwowy był sprawny, a czasem nie, moglibyśmy użyć ich do podsumowania tak zwanych "przykładowych statystyk". Na przykład, moglibyśmy zanotować w tych próbkach liczbę uruchomień samochodu, gdy samochód się nie obracał, a układ paliwowy był sprawny, i podzielić tę liczbę przez całkowitą liczbę przypadków, gdy samochód się nie uruchomił było ok. Frakcję tę można wykorzystać jako oszacowanie p (P4 ¬P2; P3). Możemy dokonać podobnych szacunków dla pozostałych trzech prawdopodobieństw i podobne szacunki prawdopodobieństw w innych CPT w sieci. Przy wystarczająco dużej kolekcji próbek oszacowania te byłyby dość wiarygodne: im większa liczba próbek, tym lepsze oszacowania. Kompilacja przykładowych statystyk (czasami uzupełniana przez dodatkowe obliczenia, których nie będę tutaj omawiać) zapewnia sposób oszacowania CPT sieci o znanej strukturze. W jaki sposób moglibyśmy poznać strukturę nieznanej sieci? Metoda obejmuje następującą sekwencję kroków:

1. Zacznij od podstawowej struktury kandydata, na przykład takiej, która nie ma połączenia między węzłami i użyj kolekcji danych do oszacowania CPT. (Przypomnijmy, że CPT węzła bez rodziców jest tylko bezwarunkowym prawdopodobieństwem dla tego węzła. Można to oszacować na podstawie ułamka razy, gdy skojarzona z nim propozycja jest prawdziwa w zbiorze danych.)
2. Oblicz "miarę dobroci" dla tej sieci. Jeden z proponowanych środków opiera się na tym, jak dobrze sieć z jej obliczonymi CPT może być wykorzystana do przesłania (tj. odtworzenia) pierwotnego zbioru danych.
3. Rozpocznij proces wyszukiwania "wspinanie się na wzgórze", oceniając "pobliskie" sieci, które różnią się od poprzedniej drobnymi zmianami (które mogą obejmować dodanie łuku, usunięcie już istniejącej i zamianę węzłów). Aby ocenić zmienione sieci, oblicza się ich CPT i zalety. Postaw na zmienioną sieć z najlepszą poprawą dobroci.
4. Kontynuuj proces wspinania się na wzgórze, dopóki nie będzie można wprowadzić żadnych ulepszeń (lub dopóki nie zostanie spełnione określone wcześniej kryterium zatrzymania). Chociaż proces ten wydaje się być dość żmudny (i tak jest), komputery mogą wykonywać ten proces wspinania się w miarę rozsądnie i wyuczono niektóre dość złożone sieci.

Jako przykład rozważmy sieci na ryc. 28.5.



Pokazane są trzy sieci. Pierwszą jest sieć kodująca relacje między 37 zmiennymi dla problemu związanego z systemem alarmowym stosowanym w zarządzaniu respiratorem na oddziale intensywnej opieki szpitalnej. Tę znaną sieć wykorzystano do wygenerowania zestawu treningowego wielkości 10.000 losowych wartości dla 37 węzłów. Korzystając z tej losowej próbki i rozpoczynając od drugiej sieci (tej bez żadnych zależności, a więc bez powiązań między węzłami), uczono się trzeciej sieci (za około pięć godzin na SUN SPARCstation 20) przy użyciu metod podobnych do tych właśnie opisanych. Zwróć uwagę na bardzo bliskie podobieństwo w strukturze {brakuje tylko jednego łuku. Czasami strukturę sieci można znacznie uprościć, dodając do sieci węzły, które reprezentują atrybuty, które nie występują w zbiorze danych. Metody uczenia się w sieci zostały rozszerzone, aby móc nauczyć się instalować "ukryte węzły", które reprezentują te wymyślone atrybuty. Atrybuty wymyślone na podstawie danych są często przydatne do pogłębienia naszego zrozumienia zjawisk, które doprowadziły do powstania danych.

Probabilistyczne modele relacyjne

Ważne opracowanie sieci bayesowskich o nazwie "Probabilistic Modele Relation "(PRM), opracował profesor Stanford , Daphne Koller wraz ze swoimi studentami Avi Pfefferem i Lise Getoor oraz współpracownikiem, Nirem Friedmanem (były student Stanforda, a obecnie profesor na Uniwersytecie Hebrajskim). Osoby o ograniczonej sprawności ruchowej integrują prawdopodobieństwo z rachunkiem predykatu. [Kilka wcześniejszych prac nad połączeniem tych dwóch form reprezentacyjnych wykonało kilku badaczy, w szczególności David Poole (z University of British Columbia.] PRM wykorzystuje fakt, że niektóre węzły w sieci może dzielić te same atrybuty, z wyjątkiem wartości zmiennych wewnętrznych dla tych atrybutów (podobnie jak fakt, że w rachunku predykatów ten sam predykat może być zapisany z różnymi wartościami dla swoich zmiennych wewnętrznych). Na przykład sieć pokazująca, że grupa krwi i informacje o chromosomie zależą od chromosomów odziedziczonych po rodzicach, powtarzałaby podsieci. Przykład pokazuję na ryc. 28.7.



W jego przypadku pojedynczy "szablon" służy do tworzenia różnych podsieci, których zmienne atrybutów są tworzone instancji dla różnych osób. Korzystanie z PRM sprawia, że projektowanie sieci bayesowskich jest znacznie bardziej wydajne niż proces projektowania każdej z nich (tylko nieznacznie różni się ) oddzielnie. Koller twierdzi, że była zmotywowana do myślenia o PRM w rozmowie ze studentem, który musiał przekształcić sieć bayesowską modelującą trzypasmową autostradę w jedną modelującą czteropasmową autostradę. Przypomina, mówiąc "…ale to tylko dodanie jeszcze jednego pasa, z pewnością możesz ponownie wykorzystać część struktury" .Struktura i CPT PRM mogą być określone przez projektanta lub wyuczone z danych. Dodatkową zaletą PRM jest to, że obiekty powstałe w wyniku tworzenia instancji zmienne szablonów można łączyć w wynikową sieć bayesowską (niektóre są na schemacie); relacje między tymi obiektami można określać ręcznie lub uczyć się. Podobnie jak w przypadku każdej sieci bayesowskiej można zastosować procedury wnioskowania probabilistycznego w celu odpowiedzi na pytania dotyczące prawdopodobieństw niektórych węzłów ze względu na te z innych. PRM i powiązane struktury były wykorzystywane w różnych aplikacjach, w tym do odzyskiwania sieci regulacyjnych z danych dotyczących ekspresji genów. Jeśli chodzi o sieci bayesowskie ogólnie, jest ich teraz wiele, wiele aplikacji {zbyt wiele aby wymienić tutaj. Aby nadać posmak ich różnorodności, wspomnę o ich zastosowaniu w badaniach genomowych, w prognozowaniu i kierowaniu ruchem samochodowym, w modelowaniu wybuchów chorób i zgadywaniu w ac Kolejne działania użytkownika komputera, aby umożliwić systemowi operacyjnemu Windows "wstępne pobranie" danych aplikacji do pamięci, zanim będzie ona wymagana. Są też firmy, które sprzedają systemy oparte na wiedzy i wnioskach sieci bayesowskich. Jedną z rzeczy, których nauczyły nas wszystkie te aplikacje, jest znaczenie ogromnych ilości danych, które według Petera Norviga, współautora wiodącego podręcznika AI i dyrektora badań w Google, okazały się głównym tematem nowoczesnej AI. W rzeczywistości Peter powiedział ,że Google jest największym na świecie systemem sztucznej inteligencji. Zapytano go, dlaczego, a on po prostu odpowiedział "dane, dane, dane", a Google ma ich więcej niż ktokolwiek ".

Tymczasowe sieci bayesowskie

Przykłady sieci bayesowskich zilustrowane w ostatnich sekcjach, wraz z większymi zastosowanymi w wielu aplikacjach, można nazwać "statycznymi". Oznacza to, że zdania i wielkości reprezentowane przez węzły i CPT są ponadczasowe w tym sensie, że dotyczą one tego samego momentu w czasie (lub wszystkich momentów w czasie). Jednak opisałem już sieć probabilistyczną, która w różnym czasie obejmuje wielkości, a mianowicie ukryte modele Markowa. W sekcji 17.3.2 wyjaśniłem, w jaki sposób HMM zostały użyte w rozpoznawaniu mowy. Jedną z powszechnych postaci HMM pokazano na rysunku


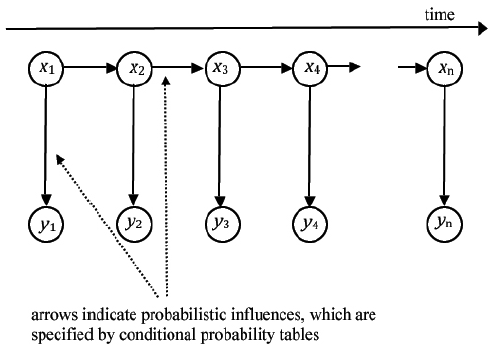
Ten schemat ma na celu pokazanie, jak sekwencja czasowa bytów, x₁; x₁; …x₁, powoduje sekwencję czasową innych bytów, y₁; y₂;… y_n. Wpływ każdego x_i na kolejne x i y jest regulowany przez prawdopodobieństwa. Łatwo zauważyć, że ta sieć jest siecią bayesowską, mimo że zaangażowane ilości występują w sekwencji czasowej. Ten konkretny HMM jest nazywany procesem Markowa pierwszego rzędu, ponieważ każdy stan zależy tylko od stanu bezpośrednio poprzedzającego. W procesach wyższego rzędu na każdy stan wpływa więcej niż jeden stan poprzedni. W sieci HMM każda x_i jest "zmienną stanu", a y_i są "zmiennymi obserwowalnymi". Zakłada się, że wartości stanów są nieznane (to znaczy "ukryte"), ale obserwowalne wartości można zmierzyć i tym samym poznać. Każdy stan powoduje związany z nim obserwowalny i następny stan. Zakładamy, że znamy tablice prawdopodobieństwa warunkowego sieci, to znaczy prawdopodobieństwa obserwowalności i następnego stanu, biorąc pod uwagę wartość stanu. Biorąc pod uwagę wartość jednego lub większej liczby obserwowalnych, możemy obliczyć zaktualizowane prawdopodobieństwa stanów za pomocą dowolnej metody obliczeniowej prawdopodobieństwa w sieci bayesowskiej. Oto przykład. Załóżmy, że warunki pogodowe samolotu na odległym lotnisku są albo mgliste, albo nie. Czujnik na lotnisku rejestruje pogodę, a nadajnik emituje sygnał co pięć minut. Sygnał ten, odbierany przez samolot próbujący wylądować na lotnisku, może czasami być w błędzie. Zatem stany, czyli x w HMM modelujące ten proces, może mieć wartości 1 lub 0, a wartość 1 oznacza mgłę. Sygnały odbierane przez samolot, y w HMM, również mają wartości 1 lub 0, przy czym wartość 1 wskazuje, że zaobserwowano mgłę. Ale obserwacje mogą być błędne. Mówiąc konkretnie, załóżmy, że prawdopodobieństwo, że następny stan ma taką samą wartość jak w obecnym stanie, wynosi 75% (mgła ma tendencję do utrzymywania się), a prawdopodobieństwo błędu jest możliwe do zaobserwowania na poziomie 5%. Prawdopodobieństwa te pozwalają na zbudowanie tabel prawdopodobieństwa warunkowego sieci bayesowskiej. (Przykład można uczynić bardziej realistycznym, pozwalając każdemu stanowi odzwierciedlić stopień zamglenia i zależą od stanów oprócz pojedynczego stanu poprzedzającego.) Pilot statku powietrznego musi podjąć decyzję o próbie wylądowania lub nie w oparciu o kolejność otrzymanych y. Na przykład, on lub ona może chcieć poznać prawdopodobieństwo, że lądowisko jest teraz mgliste na podstawie sekwencji wcześniejszych obserwacji, aż do obecnej. W języku HMM operacja obliczająca to prawdopodobieństwo nazywa się "filtrowaniem". Alternatywnie, pilot może chcieć obliczyć prawdopodobieństwo, że lądowanie będzie mgliste za 10 minut na podstawie tych obserwacji. Ta operacja nazywa się "prognozowaniem". Chociaż pilot nie przydałby się wiele, może być ciekawy prawdopodobieństwa, że 10 minut temu pas lądowania był zamglony na podstawie sekwencji obserwacji do chwili obecnej. Ta operacja nazywa się "wygładzaniem". W mojej dyskusji na temat rozpoznawania mowy w rozdziale 17.3.2 wspomniałem, że stany HMM odpowiadają pojedynczym słowom, a obserwacje odpowiadają segmentom kształtu fali. W tej aplikacji chcemy obliczyć najbardziej prawdopodobną sekwencję słów, biorąc pod uwagę wszystkie obserwacje przebiegów do chwili obecnej. Wszystkie te obliczenia - filtrowanie, przewidywanie, wygładzanie i najbardziej prawdopodobna sekwencja stanów - mogą być wykonywane przy użyciu procedur wnioskowania sieci bayesowskich . Istnieje kilka wyspecjalizowanych wersji, z których niektóre pochodzą z terenów spoza AI. Zależą one od aplikacji i danych sieci. Spośród nich mogę wspomnieć (ale nie będę próbował tutaj wyjaśniać) algorytm przewijania do przodu, algorytm Viterbiego i filtrowanie Kalmana. Odważny matematycznie czytelnik może znaleźć jasne wyjaśnienia w doskonałym podręczniku Russella i Norviga. Fakt, że pełne wyjaśnienia wiążą się z dość złożoną matematyką, ponownie świadczy o wielkim wzroście technicznej głębi sztucznej inteligencji, który rozpoczął się w latach 80. HMM, w tym mój mglisty / nie-zamglony przykład, mają tylko jedną zmienną stanu w każdej chwili. Możliwe jest budowanie sieci, w których za każdym razem jest więcej zmiennych stanu {z których wszystkie wpływają na siebie nawzajem, obserwacje i kolejne zmienne stanu. Są one zwykle nazywane "dynamicznymi sieciami bayesowskimi" (DBN) i zostały po raz pierwszy zbadane w AI przez Thomasa Deana i Keiji Kanazawa. Dodatkowe zmienne stanu i obserwacji sprawiają, że dokładne obliczenia są trudne, ale opracowano kilka praktycznych przybliżonych metod, takich jak "filtrowanie cząstek" (które opiszę bardziej szczegółowo później). Podobnie jak w przypadku zwykłych sieci bayesowskich, DBN można nauczyć się z baz danych zawierających informacje o procesach czasowych. Wykorzystano je przede wszystkim w kilku aplikacjach te wymagające percepcji. Jednym z nich jest przetwarzanie filmów, w których można wykorzystywać probabilistyczne zależności między klatkami do rozpoznawania i śledzenia poruszających się obiektów. Innym jest certyfikacja systemów unikania kolizji dla załogowych i bezzałogowych statków powietrznych. Chociaż ten rozdział dotyczy sieci bayesowskich, są one tylko jednym rodzajem ważnej ogólnej klasy zwanej "probabilistycznymi modelami graficznymi. "Losowe pola Markowa, często nazywane sieciami Markowa, są kolejnym członkiem tej klasy, w której połączenia między węzłami są niekierunkowe. Zostały one pierwotnie opracowane w celu rozwiązywania problemów w fizyce statystycznej, a teraz znajdują zastosowanie w wielu obszarach, w tym w przetwarzaniu obrazu, percepcji sensorycznej i modelowaniu mózgu. Istnieją również sposoby interpretacji innych sieci neuronowych jako przykładów probabilistycznych modeli graficznych.