Jak wspomniano, zebraliśmy wszystkie dane do głosowania imiennego Senatu na kongresach 101. do 111. i umieściliśmy je w katalogu danych. Jak zrobiliśmy w całym tym tekście, rozpoczniemy to studium przypadku, ładując dane i sprawdzając je. W tym procesie wykorzystamy dwie biblioteki R: po pierwsze, bibliotekę zagraniczną, które omówimy za chwilę; a po drugie, ggplot2, którego użyjemy do wizualizacji wyników algorytmu MDS. Pliki znajdują się w data / roll_call /, więc używamy funkcji list.files do generowania wektora znakowego o nazwie data.files ze wszystkimi nazwami plików danych.
library(foreign)
library(ggplot2)cac
data.dir <- “data/roll_call/”
data.files <- list.files(data.dir)
Kiedy sprawdzamy zmienną data.files, widzimy, że rozszerzenie plików danych różni się od plików tekstowych, których używaliśmy do naszych studiów przypadków w poprzednich częściach. Rozszerzenie .dta odpowiada plikowi danych Stata. Stata to komercyjny program do obliczeń statystycznych, który okazuje się być bardzo popularny wśród naukowców, szczególnie naukowców. Ponieważ Poole i Rosenthal postanowili rozpowszechnić dane w tym formacie, więc będziemy potrzebować sposobu załadowania tych danych do R.
data.files
[1] “sen101kh.dta” “sen102kh.dta”
[3] “sen103kh.dta” “sen104kh.dta”
[5] “sen105kh.dta” “sen106kh.dta”
[7] “sen107kh.dta” “sen108kh_7.dta”
[9] “sen109kh.dta” “sen110kh_2008.dta”
[11] “sen111kh.dta”
Wprowadź obcy pakiet, który jest przeznaczony do odczytu dużej liczby egzotycznych plików danych do ramek danych R, w tym S, SAS, SPSS, Systat, dBase i wielu innych. Do naszych celów wykorzystamy funkcję read.dta, która jest przeznaczona do odczytu plików Stata. Na potrzeby tej analizy chcemy przeanalizować dane dla 10 kongresów, od 101 do 111. Wszystkie te dane przechowamy w jednym obiekcie, którym można manipulować jednocześnie. Jak zobaczymy, te zestawy danych są stosunkowo małe, więc w tym przypadku nie martwimy się o pamięć. Aby połączyć nasze zestawy danych, użyjemy funkcji lapply w połączeniu z read.dta.
rollcall.data <- lapply(data.files,
function(f) read.dta(paste(data.dir, f, sep=””), convert.factors=FALSE))
Mamy teraz wszystkie 10 ramek danych głosowań imiennych w zmiennej rollcall.data. Kiedy sprawdzamy wymiar pierwszej ramki danych, 101. kongresu, widzimy, że ma ona 103 wiersze i 647 kolumn. Po dalszym sprawdzeniu nagłówka tej ramki danych możemy zobaczyć, co znajduje się w tych wierszach i kolumnach. Podczas sprawdzania głowy danych należy zwrócić uwagę na dwie ważne rzeczy. Po pierwsze, każdy wiersz odpowiada wyborcy w Senacie USA. Po drugie, pierwsze dziewięć kolumn ramki danych zawiera informacje identyfikacyjne dla tych wyborców, a pozostałe kolumny to rzeczywiste głosy. Zanim przejdziemy dalej, musimy zrozumieć te informacje identyfikacyjne.
dim(rollcall.data[[1]])
[1] 103 647
head(rollcall.data[[1]])
cong id state dist lstate party eh1 eh2 name V1 V2 V3 … V638
1 101 99908 99 0 USA 200 0 0 BUSH 1 1 1 … 1
2 101 14659 41 0 ALABAMA 100 0 1 SHELBY, RIC 1 1 1 … 6
3 101 14705 41 0 ALABAMA 100 0 1 HEFLIN, HOW 1 1 1 … 6
4 101 12109 81 0 ALASKA 200 0 1 STEVENS, TH 1 1 1 … 1
5 101 14907 81 0 ALASKA 200 0 1 MURKOWSKI, 1 1 1 … 6
6 101 14502 61 0 ARIZONA 100 0 1 DECONCINI, 1 1 1 … 6
Niektóre kolumny są dość oczywiste, takie jak lstate i name, ale co z eh1 i eh2? Na szczęście Poole i Rosenthal udostępniają książkę kodów dla wszystkich danych apelowych. Książka kodów dla 101. kongresu znajduje się na stronie http://www.voteview.com/senate101. Ten słownik kodów jest szczególnie pomocny ponieważ wyjaśnia nie tylko, co zawiera każda z pierwszych dziewięciu kolumn, ale także sposób kodowania każdego z głosów, na co będziemy musieli wkrótce zwrócić uwagę.
- Numer kongresu
- Numer identyfikacyjny ICPSR: 5-cyfrowy kod przypisany przez ICPSR, poprawiony przez Howarda Rosenthala i mnie.
- Kod stanu: 2-cyfrowy kod stanu ICPSR.
- Numer dystryktu kongresowego (0, jeśli Senat)
- Nazwa stanu
- Kod imprezy: 100 = Dem., 200 = Repub. (Patrz PARTY3.DAT)
- Obłożenie: Kod zajętości ICPSR – 0 = tylko mieszkaniec; 1 = 1. mieszkaniec; 2 = 2. mieszkaniec; itp.
- Ostatni sposób objęcia urzędu: Kodeks zdobycia urzędu ICPSR – 1 = wybory powszechne;
2 = wybory specjalne; 3 = wybrany przez ustawodawcę stanowego; 5 = wyznaczony
- Imię i nazwisko
10 – do liczby apeli + 10: dane apeli –
0 = nie jest członkiem, 1 = Tak, 2 = Sparowane Tak, 3 = Ogłoszono Tak,
4 = nie ogłoszono, 5 = powiązano, 6 = nie,
7 = Obecne (niektóre kongresy, również nieużywane niektóre kongresy),
8 = Obecne (niektóre Kongresy, również nie korzystały z niektórych Kongresów),
9 = Nie głosować
Do naszych celów jesteśmy zainteresowani jedynie nazwiskami wyborców, ich przynależnością do partii i ich faktycznymi głosami. Z tego powodu naszym pierwszym krokiem jest uzyskanie danych głosowania imiennego w formie, z której możemy stworzyć rozsądną miarę odległości od głosów. Jak widać w przykładzie 9-1, głosowanie imienne w Senacie nie jest po prostu tak lub nie; istnieją ogłoszone i sparowane formy głosów Yea i Nay, a także Obecne głosy, to znaczy głosy, w których senator wstrzymał się od głosowania nad konkretnym projektem ustawy, ale był obecny w czasie głosowania. Są też chwile, kiedy senatorzy po prostu nie byli obecni, aby oddać głos, ani nawet nie zostali wybrani do Senatu. Biorąc pod uwagę różnorodność możliwych głosów, w jaki sposób bierzemy te dane i przekształcamy je w coś, co możemy łatwo wykorzystać do pomiaru odległości między senatorami? Jednym z podejść jest uproszczenie kodowania danych poprzez agregację podobnych typów głosów. Na przykład głosowanie w parach jest procedurą, w ramach której członkowie Kongresu wiedzą, że nie będą obecni podczas danego głosowania imiennego, a ich głos może zostać „sparowany” z innym członkiem, który głosuje przeciwnie. To, wraz z ogłoszonymi głosowaniami, jest środkiem parlamentarnym dla Senatu lub Izby w celu ustalenia kworum do przeprowadzenia głosowania. Dla naszych celów jesteśmy jednak mniej zainteresowani mechanizmem, w którym głosowanie się odbyło, a raczej zamierzonym wynikiem głosowania, tj. Za lub przeciw. Jako taki, jedną metodą agregacji byłoby grupowanie wszystkich typów Yea i Nay razem. Zgodnie z tą samą logiką możemy zgrupować wszystkie typy, które nie oddają głosu.
rollcall.simplified <- function(df) {
no.pres <- subset(df, state < 99)
for(i in 10:ncol(no.pres)) {
no.pres[,i] <- ifelse(no.pres[,i] > 6, 0, no.pres[,i])
no.pres[,i] <- ifelse(no.pres[,i] > 0 & no.pres[,i] < 4, 1, no.pres[,i])
no.pres[,i] <- ifelse(no.pres[,i] > 1, -1, no.pres[,i])
}
return(as.matrix(no.pres[,10:ncol(no.pres)]))
}
rollcall.simple <- lapply(rollcall.data, rollcall.simplified)
Rysunek
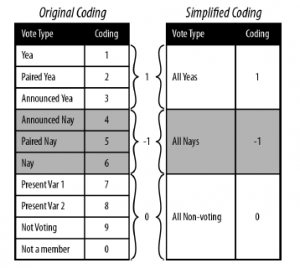
ilustruje procedurę, którą zastosujemy w celu uproszczenia kodowania z Poole i Rosenthal, która zostanie wykorzystana w naszej analizie. Podobnie jak w symulowanym przykładzie w poprzedniej sekcji, zakodujemy wszystkie Yeas jako +1, wszystkie Nays jako –1, a wszystkie obserwacje bez głosu jako 0. To pozwala na bardzo proste zastosowanie kodowania danych do metryki odległości. Teraz musimy przekonwertować dane na nasze nowe kodowanie. Musimy także wyodrębnić tylko głosy z ramki danych, abyśmy mogli wykonać niezbędną manipulację macierzą. Aby to zrobić, definiujemy funkcję rollcall.simplified, która przyjmuje ramkę danych wywołania roll jako swój jedyny argument i zwraca matrycę senator według głosów z naszym uproszczonym kodowaniem. Zauważysz, że pierwszy krok w tej funkcji usuwa wszystkie obserwacje, w których kolumna stanu jest równa 99. Kod stanu 99 odpowiada wiceprezydentowi Stanów Zjednoczonych, a ponieważ wiceprezydent bardzo rzadko głosuje, usuwamy go. Następnie używamy polecenia ifelse, aby wykonać wektoryzowane porównanie numeryczne dla wszystkich kolumn w pozostałej macierzy. Pamiętaj, że kolejność, w jakiej dokonujemy tego porównania, ma znaczenie. Zaczynamy od ustawienia wszystkich nonvotes (wszystko powyżej 6) na zero. Możemy wtedy szukać głosów zakodowanych powyżej 0 i mniej niż 4, Yeas, i przekonwertować je na 1. W końcu wszystko większe niż 4 to NIE, więc kodujemy je jako –1. Mamy teraz dane apelowe w tej samej formie, w jakiej zaczęliśmy dla naszych danych symulowanych z poprzedniej sekcji, i możemy kontynuować te dane dokładnie tak samo, jak w przypadku danych symulowanych recenzji konsumenckich. W następnej i ostatniej sekcji wygenerujemy MDS tych danych i zbadamy je wizualnie.