Rysunek
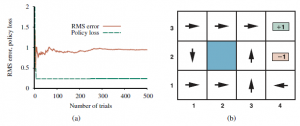
przedstawia wyniki jednej sekwencji prób dla agenta ADP, która na każdym kroku jest zgodna z zaleceniem optymalnej polityki dla wyuczonego modelu. Agent nie uczy się prawdziwych narzędzi ani prawdziwej optymalnej polityki! Zamiast tego dzieje się tak, że w trzeciej próbie znajduje politykę, która osiąga nagrodę +1 na niższej trasie przez (2,1), (3,1), (3,2) i (3,3). (Patrz Rysunek (b). Po eksperymentowaniu z drobnymi zmianami, od ósmej próby dalej trzyma się tej polityki, nigdy nie ucząc się użyteczności innych stanów i nigdy nie znajdując optymalnej trasy przez (1, 2), (1, 3) i (2,3). Nazwiemy tego agenta zachłannym agentem, ponieważ na każdym kroku zachłannie podejmuje działania, które obecnie uważa za optymalne. Czasami chciwość się opłaca i agent dąży do optymalnej polityki, ale często tak się nie dzieje. Jak to możliwe, że wybór optymalnego działania prowadzi do nieoptymalnych wyników? Odpowiedź brzmi, że wyuczony model nie jest tym samym, co prawdziwe środowisko; co jest optymalne w nauczonym model może zatem być nieoptymalny w rzeczywistym środowisku. Niestety, agent nie wie, czym jest prawdziwe środowisko, więc nie może obliczyć optymalnego działania dla prawdziwego środowiska. Co więc powinien zrobić? Chciwy agent przeoczył fakt, że działania nie tylko zapewniają nagrody; dostarczają również informacji w postaci perceptów w powstałych stanach. Jak widzieliśmy w przypadku problemów z bandytami w sekcji 16.3, agent musi dokonać kompromisu między wykorzystaniem aktualnie najlepszej akcji, aby zmaksymalizować swoją krótkoterminową nagrodę, a eksploracją wcześniej nieznanych stanów w celu uzyskania informacji, które mogą prowadzić do zmiany polityki (i do większe nagrody w przyszłości). W prawdziwym świecie nieustannie trzeba wybierać między kontynuowaniem wygodnej egzystencji, a wyruszeniem w nieznane w nadziei na lepsze życie. Chociaż problemy z bandytami są trudne do rozwiązania dokładnie w celu uzyskania optymalnego schematu eksploracji, możliwe jest jednak wymyślenie schematu, który ostatecznie odkryje optymalną politykę, nawet jeśli może to potrwać dłużej niż jest to optymalne. Każdy taki schemat nie powinien być zachłanny w odniesieniu do najbliższego następnego ruchu, ale powinien być tak zwany „chciwy w granicy nieskończonej eksploracji” lub GLIE. Schemat GLIE musi wypróbować każdą akcję w każdym stanie nieograniczoną liczbę razy, aby uniknąć skończonego prawdopodobieństwa pominięcia optymalnej akcji. Agent ADP korzystający z takiego schematu w końcu nauczy się prawdziwego modelu przejścia, a następnie będzie mógł działać w warunkach eksploatacji. Istnieje kilka schematów GLIE; jednym z najprostszych jest nakłonienie agenta do wybrania losowej akcji w kroku czasowym t z prawdopodobieństwem 1=t, aw przeciwnym razie przestrzeganie polityki zachłanności. Chociaż ostatecznie zbiega się to do optymalnej polityki, może być powolne. Lepsze podejście nadałoby pewną wagę działaniom, których agent nie próbował zbyt często, jednocześnie unikając działań, które są uważane za mało użyteczne (tak jak zrobiliśmy to w przypadku przeszukiwania drzewa Monte Carlo). Można to zaimplementować zmieniając równanie ograniczające , tak aby przypisało wyższe oszacowanie użyteczności stosunkowo niezbadanym parom stan-działanie. To sprowadza się do optymistycznego wyprzedzenia możliwych środowisk i powoduje, że agent początkowo zachowuje się tak, jakby wszędzie były rozrzucone wspaniałe nagrody. Użyjmy U+(s) do oznaczenia optymistycznego oszacowania użyteczności (tj. oczekiwanej nagrody za przejście) stanu s i niech N(s;a) będzie liczbą prób działania a w stan s. Załóżmy, że używamy iteracji wartości w agencie uczącym ADP; następnie musimy przepisać równanie aktualizacji , aby uwzględnić optymistyczne oszacowanie:
![]()
Tutaj f jest funkcją eksploracji. Funkcja f (u,n) określa, w jaki sposób chciwość (preferencja wysokich wartości użyteczności u) jest wymieniana na ciekawość (preferowanie działań, które nie były często podejmowane i mają małą liczbę n). Funkcja powinna rosnąć w u i maleć w n. Oczywiście istnieje wiele możliwych funkcji, które pasują do tych warunków. Jedna szczególnie prosta definicja to:
![]()
gdzie R+ to optymistyczne oszacowanie najlepszej możliwej nagrody możliwej do uzyskania w dowolnym stanie, a Ne to stały parametr. Spowoduje to, że agent spróbuje każdej pary stan-działanie co najmniej Ne razy. Bardzo ważny jest fakt, że po prawej stronie równania pojawia się U+, a nie U. W miarę postępu eksploracji stany i działania w pobliżu stanu początkowego mogą być wypróbowywane wiele razy. Gdybyśmy użyli U, bardziej pesymistycznego oszacowania użyteczności, wówczas agent wkrótce byłby niechętny do eksploracji dalej. Użycie U+ oznacza, że korzyści z eksploracji są propagowane z obrzeży niezbadanych regionów, dzięki czemu działania prowadzące do niezbadanych regionów są ważone wyżej, a nie tylko działania, które same w sobie są nieznane. Skutki tej polityki poszukiwań widać wyraźnie na wykresie (b),
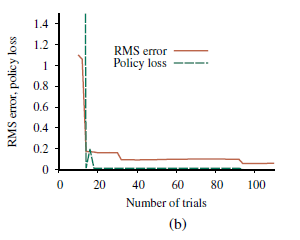
który pokazuje szybką konwergencję w kierunku zerowej utraty polityki, w przeciwieństwie do podejścia zachłannego. Bardzo prawie optymalną politykę można znaleźć już po 18 próbach. Zauważ, że błąd RMS w szacunkach użyteczności nie jest zbieżny tak szybko. Dzieje się tak, ponieważ agent dość szybko przestaje eksplorować niewdzięczne części przestrzeni stanu, a następnie odwiedza je tylko „przypadkowo”. Jednak ma sens, aby agent nie dbał o dokładną użyteczność stanów, o których wie, że są niepożądane i można ich uniknąć. Nie ma większego sensu poznawanie najlepszej stacji radiowej do słuchania spadając z klifu.