Podstawową ideą jest zrozumienie, w jaki sposób zwykłe sieci bayesowskie i RPM potrafią zdefiniować unikalny model prawdopodobieństwa i przenieść ten wgląd na ustawienie pierwszego rzędu. W istocie sieć Bayesa generuje każdy możliwy świat, zdarzenie po zdarzeniu, w porządku topologicznym określonym przez strukturę sieci, gdzie każde zdarzenie jest przypisaniem wartości do zmiennej. RPM rozszerza to na całe zestawy zdarzeń, zdefiniowane przez możliwe wystąpienia zmiennych logicznych w danym predykacie lub funkcji. OUPM idą dalej, zezwalając na kroki generatywne, które dodają obiekty do możliwego świata w budowie, gdzie liczba i typ obiektów może zależeć od obiektów, które już znajdują się w tym świecie oraz ich właściwości i relacji. Oznacza to, że generowane zdarzenie nie jest przypisaniem wartości do zmiennej, ale samym istnieniem obiektów. Jednym ze sposobów wykonania tego w jednostkach OUPM jest podanie instrukcji liczbowych, które określają rozkłady warunkowe na liczbach obiektów różnego rodzaju. Na przykład w domenie rekomendacji książek możemy chcieć odróżnić klientów (prawdziwych ludzi) od ich identyfikatorów logowania. (Tak naprawdę to identyfikatory logowania dają rekomendacje, a nie klienci!) Załóżmy (dla uproszczenia), że liczba klientów jest taka sama w zakresie od 1 do 3, a liczba książek jest taka sama w zakresie od 2 do 4:
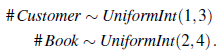
Oczekujemy, że uczciwi klienci będą mieli tylko jeden identyfikator, podczas gdy nieuczciwi klienci mogą mieć od 2 do 5 identyfikatorów:
![]()
Ta instrukcja liczbowa określa rozkład na liczbę identyfikatorów logowania, dla których klient c jest Właścicielem. Funkcja Owner jest nazywana funkcją pochodzenia, ponieważ mówi skąd pochodzi każdy obiekt wygenerowany przez tę instrukcję liczby. W przykładzie w poprzednim akapicie zastosowano równomierny rozkład liczb całkowitych od 2 do 5 w celu określenia liczby logowań dla nieuczciwego klienta. Ten szczególny rozkład jest ograniczony, ale ogólnie rzecz biorąc, liczba obiektów może nie być a priori ograniczona. Najczęściej używanym rozkładem na nieujemne liczby całkowite jest rozkład Poissona. Poisson ma jeden parametr, który jest oczekiwaną liczbą obiektów, a zmienna X pobrana z Poisson(λ) ma następujący rozkład:
![]()
Wariancja Poissona również wynosi λ , więc odchylenie standardowe wynosi √λ . Oznacza to, że dla dużych wartości λ , rozkład jest wąski w stosunku do średniej – na przykład, jeśli liczba mrówek w gnieździe jest modelowana przez Poissona ze średnią wynoszącą jeden milion, odchylenie standardowe wynosi tylko tysiąc lub 0,1%. W przypadku dużych liczb często bardziej sensowne jest użycie dyskretnego rozkładu logarytmiczno-normalnego, który jest odpowiedni, gdy logarytm liczby obiektów ma rozkład normalny. Szczególnie intuicyjna forma, którą nazywamy rozkładem rzędu wielkości, używa logów do podstawy 10: zatem rozkład OM(3,1) ma średnią 103 i odchylenie standardowe jednego rzędu wielkości, tj. masy prawdopodobieństwa mieści się między 102 a 104. Formalna semantyka OUPM zaczyna się od definicji obiektów, które zaludniają możliwe światy. W standardowej semantyce typizowanej logiki pierwszego rzędu obiekty są po prostu ponumerowanymi tokenami z typami. W OUPM każdy obiekt to historia generacji; na przykład obiekt może być „czwartym identyfikatorem logowania siódmego klienta”. (Przyczyna tej nieco barokowej konstrukcji stanie się wkrótce jasna.) Dla typów bez funkcji początku obiekty mają puste źródło; na przykład <Klient; ;2i> odnosi się do drugiego klienta wygenerowanego z tego numeru. W przypadku instrukcji liczbowych z funkcjami początku , każdy obiekt zapisuje swój początek; na przykład obiekt <LoginID; <Owner; <Klient; ;2>>;3> to trzeci login należący do drugiego klienta.
Zmienne liczbowe OUPM określają, ile jest obiektów każdego typu z każdym możliwym pochodzeniem w każdym możliwym świecie; zatem #LoginID<Owner;hCustomer; ;2>>(ω)=4 oznacza, że w świecie ω, klient 2 posiada 4 identyfikatory logowania. Podobnie jak w relacyjnych modelach prawdopodobieństwa, podstawowe zmienne losowe wyznaczają wartości predykatów i funkcji dla wszystkich krotek obiektów; zatem, Uczciwy<Klient; ;2>ω)=true oznacza, że w świecie ω, klient 2 jest uczciwy. Świat możliwy jest zdefiniowany przez wartości wszystkich zmiennych liczbowych i podstawowych zmiennych losowych. Świat może zostać wygenerowany z modelu przez próbkowanie w porządku topologicznym; Rysunek przedstawia przykład.
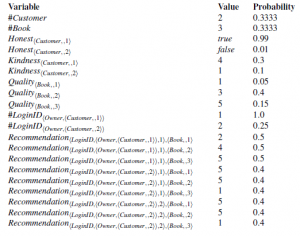
Prawdopodobieństwo tak skonstruowanego świata jest iloczynem prawdopodobieństw dla wszystkich wartości próbkowanych; w tym przypadku 1,2672 x 10-11. Teraz staje się jasne, dlaczego każdy obiekt zawiera swój początek: ta właściwość zapewnia, że każdy świat może być skonstruowany przez dokładnie jedną sekwencję generacji. Gdyby tak nie było, prawdopodobieństwo istnienia świata byłoby nieporęczną sumą kombinatoryczną wszystkich możliwych sekwencji generacji, które go tworzą. Modele otwartego wszechświata mogą mieć nieskończenie wiele zmiennych losowych, więc pełna teoria obejmuje nietrywialne rozważania z zakresu teorii miary. Na przykład instrukcje liczbowe z rozkładami Poissona lub rzędu wielkości pozwalają na nieograniczoną liczbę obiektów, co prowadzi do nieograniczonej liczby zmiennych losowych dla właściwości i relacji tych obiektów. Co więcej, OUPM mogą mieć zależności rekurencyjne i nieskończone typy (liczby całkowite, łańcuchy itp.). Wreszcie, dobre ukształtowanie nie pozwala na cykliczne zależności i nieskończenie oddalające się łańcuchy przodków; warunki te są na ogół nierozstrzygalne, ale pewne warunki wystarczające syntaktycznie można łatwo sprawdzić.