Podstawowym założeniem teorii gier kooperacyjnych jest to, że gracze będą podejmować strategiczne decyzje dotyczące tego, z kim będą współpracować. Intuicyjnie gracze nie będą chcieli pracować z nieproduktywnymi graczami — będą naturalnie szukać graczy, którzy wspólnie zapewniają wysoką wartość koalicyjną. Ale ci poszukiwani gracze będą prowadzić własne rozumowanie strategiczne. Zanim będziemy mogli opisać to rozumowanie, potrzebujemy kilku dalszych definicji. Imputacja dla gry kooperacyjnej (N,v) to wektor wypłaty, który spełnia dwa następujące warunki:

Pierwszy warunek mówi, że przypisanie musi rozdzielić całkowitą wartość wielkiej koalicji; drugi warunek, zwany racjonalnością indywidualną, mówi, że każdy gracz ma się przynajmniej tak dobrze, jakby działał sam. Biorąc pod uwagę przypisanie x = (x1,…xn) i koalicję C ⊆ N, definiujemy x(C) jako sumę Σi C xi – całkowitą kwotę wypłaconą C przez przypisanie x. Następnie definiujemy rdzeń gry (N,v) jako zbiór wszystkich imputacji x spełniających warunek x(C) ≥ v(C) dla każdej możliwej koalicji C ⊂ N. Tak więc, jeśli imputacja x nie jest w rdzeniu, to istnieje jakaś koalicja C ⊂ N taka, że v(C) > x(C). Gracze w C odmówiliby przyłączenia się do wielkiej koalicji, ponieważ lepiej byłoby, gdyby trzymali się C. Rdzeń gry składa się zatem ze wszystkich możliwych wektorów wypłat, którym żadna koalicja nie mogłaby się sprzeciwić, ponieważ mogliby sobie radzić lepiej, nie przystąpienie do wielkiej koalicji. Tak więc, jeśli rdzeń jest pusty, to wielka koalicja nie może się utworzyć, ponieważ niezależnie od tego, jak wielka koalicja podzieliłaby swoje wypłaty, jakaś mniejsza koalicja odmówiłaby przystąpienia. Główne pytania obliczeniowe wokół rdzenia dotyczą tego, czy jest pusta, oraz czy dany rozkład wypłat znajduje się w rdzeniu. Definicja rdzenia w naturalny sposób prowadzi do układu nierówności liniowych, jak następuje (niewiadomymi są zmienne x1,…,xn, a wartości nv(C) są stałymi):

Każde rozwiązanie tych nierówności zdefiniuje przypisanie w rdzeniu. Możemy sformułować nierówności jako program liniowy, używając fikcyjnej funkcji celu (na przykład maksymalizując ![]()
która pozwoli nam obliczyć wielomiany w czasie w liczbie nierówności. Trudność polega na tym, że daje to wykładniczą liczbę nierówności (po jednej na każdą z 2n możliwych koalicji). W ten sposób podejście to daje algorytm sprawdzania braku pustego rdzenia, który działa w czasie wykładniczym. To, czy możemy zrobić coś lepszego, zależy od badanej gry: dla wielu klas gry kooperacyjnej problem sprawdzania niepustości rdzenia jest współ-NP-zupełny. Poniżej podajemy przykład. Zanim przejdziemy dalej, zobaczmy przykład gry superaddytywnej z pustym rdzeniem. Gra ma trzech graczy N = {1,2,3} i ma charakterystyczną funkcję określoną w następujący sposób:
![]()
Rozważmy teraz wszelkie przypisania (x1,x2,x3) dla tej gry. Ponieważ v(N) = 1, musi być tak, że co najmniej jeden gracz i ma xi > 0, a pozostali dwaj uzyskują całkowitą wypłatę mniejszą niż 1. Ci dwaj mogliby zyskać tworząc koalicję bez gracza i i dzieląc się wartość 1 między sobą. Ale ponieważ dotyczy to wszystkich imputacji, rdzeń musi być pusty. Rdzeń formalizuje ideę, że wielka koalicja jest stabilna, w tym sensie, że żadna koalicja nie może z niej z zyskiem odejść. Jednak rdzeń może zawierać nieuzasadnione imputacje w tym sensie, że jeden lub więcej graczy może uważać, że są niesprawiedliwi. Załóżmy, że N = {1,2} i mamy funkcję charakterystyczną n zdefiniowaną następująco:
![]()
Tutaj współpraca daje nadwyżkę 10 w stosunku do tego, co gracze mogliby uzyskać pracując w izolacji, więc intuicyjnie współpraca będzie miała sens w tym scenariuszu. Teraz łatwo zauważyć, że przypisanie (6;14) jest rdzeniem tej gry: żaden z graczy nie może odejść, aby uzyskać wyższą użyteczność. Ale z punktu widzenia gracza 1 może się to wydawać nierozsądne, ponieważ daje 9/10 nadwyżki graczowi 2. Zatem pojęcie rdzenia mówi nam, kiedy może powstać wielka koalicja, ale nie mówi nam jak rozłożyć wypłatę. Wartość Shapleya jest elegancką propozycją podziału wartości v(N) pomiędzy graczy, biorąc pod uwagę, że powstała wielka koalicja N. Sformułowana przez laureata Nagrody Nobla Lloyda Shapleya na początku lat pięćdziesiątych, wartość Shapleya ma być systemem sprawiedliwej dystrybucji. Co oznacza uczciwy? Rozkładanie v(N) na podstawie koloru oczu graczy, ich płci lub koloru skóry byłoby niesprawiedliwe. Studenci często sugerują, że wartość v(N) powinna być podzielona równo, co wydaje się być sprawiedliwe, dopóki nie uznamy, że dałoby to taką samą nagrodę graczom, którzy wnoszą duży wkład i graczom, którzy nie wnoszą nic. Spostrzeżenia Shapleya sugerowały, że jedynym sprawiedliwym sposobem podzielenia wartości v(N) było zrobienie tego w zależności od tego, ile każdy gracz przyczynił się do stworzenia wartości v(N). Najpierw musimy zdefiniować pojęcie marginalnego wkładu gracza. Krańcowy wkład gracza i do koalicji C to wartość, którą dodałbym (lub odjął), gdybym dołączył do koalicji C. Formalnie marginalny wkład gracza i do koalicji C jest oznaczony przez mci(C):
![]()
Teraz pierwszą próbą zdefiniowania schematu podziału wypłat zgodnie z sugestią Shapleya, że gracze powinni być nagradzani zgodnie z ich wkładem, byłaby zapłacenie każdemu graczowi wartości, którą dodaliby do koalicji zawierającej wszystkich innych graczy:
mci(N-{1})
- Problem polega na tym, że zakłada się domyślnie, że gracz i jest ostatnim graczem, który wchodzi do koalicji. Tak więc, zasugerował Shapley, musimy rozważyć wszystkie możliwe sposoby, w jakie mogłaby utworzyć się wielka koalicja, to znaczy wszystkie możliwe porządki graczy N, i wziąć pod uwagę wartość, jaką i dodaje do poprzednich graczy w kolejności. Następnie gracz powinien zostać nagrodzony poprzez otrzymanie średniego marginalnego wkładu, jaki wnosi gracz i, we wszystkich możliwych kolejnościach graczy, do zestawu graczy poprzedzających i w kolejności. Niech P oznacza wszystkie możliwe permutacje (np. uporządkowania) graczy N, a członków P przez p, p’,…, itd. Gdzie p ∈ P oraz i ∈ N, przez pi oznaczamy zbiór graczy poprzedzających i w porządku p. Wtedy wartość Shapleya dla gry G to imputacja φ(G) = (φ1(G),…, φn(G)) zdefiniowana w następujący sposób:
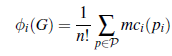
To powinno Cię przekonać, że wartość Shapleya jest rozsądną propozycją. Ale niezwykłym faktem jest to, że jest to unikalne rozwiązanie zestawu aksjomatów charakteryzujących „sprawiedliwy” schemat dystrybucji wypłat. Potrzebujemy więcej definicji przed zdefiniowaniem aksjomatów. Wirtualnego gracza definiujemy jako gracza i, który nigdy nie dodaje żadnej wartości do koalicji — to znaczy, mci(C) = 0 dla wszystkich C ⊆ N – 1. Powiemy, że dwaj gracze i oraz j są graczami symetrycznymi, jeśli zawsze wnoszą identyczny wkład do koalicji – czyli mci(C) = mcj(C) dla wszystkich C ⊆ N – {i,j}. Wreszcie, gdzie G = (N, v) i G’ = (N,v’) są grami z tym samym zestawem graczy, gra G+G’ jest grą z tym samym zestawem graczy i charakterystyczną funkcją v’’ określoną przez v’’(C) = n(C)+n’(C). Biorąc pod uwagę te definicje, możemy zdefiniować aksjomaty uczciwości spełnione przez wartość Shapleya:
• Sprawność: ![]() (Cała wartość powinna być rozdzielona).
(Cała wartość powinna być rozdzielona).
- Wirtualny gracz: Jeśli i jest fikcyjnym graczem w G, wtedy φi(G) = 0. (Gracze, którzy nigdy nic nie wnoszą, nigdy nie powinni niczego otrzymywać).
- Symetria: Jeśli i oraz j są symetryczne w G, to φi(G) = φj(G). (Gracze, którzy wnoszą identyczne wkłady, powinni otrzymać identyczne wypłaty.)
- Addytywność: Wartość jest addytywna w stosunku do gier: dla wszystkich gier G=(N,v) i G’ =(N,v’) oraz dla wszystkich graczy i N mamy φi(G+G’) = φi(G)+φi(G’).
Aksjomat addytywności jest wprawdzie dość techniczny. Jeśli jednak przyjmiemy to jako wymóg, możemy ustalić następującą kluczową właściwość: wartość Shapleya jest jedynym sposobem dystrybucji wartości koalicyjnej J, aby spełnić te aksjomaty sprawiedliwości.