Struktury i wyniki koalicji

Konwencjonalnie określa się podzbiór graczy C jako koalicję. W codziennym użyciu termin „koalicja” oznacza zbiór ludzi o wspólnej sprawie (takiej jak Koalicja na rzecz Stop Gun Violence), ale każdy podzbiór graczy będziemy nazywać koalicją. Zestaw wszystkich graczy N jest znany jako wielka koalicja. W naszym modelu każdy gracz musi wybrać dołączenie dokładnie do jednej koalicji (która może być koalicją tylko jednego gracza). W ten sposób koalicje tworzą podział zbioru graczy. Rozbiór nazywamy strukturą koalicyjną. Formalnie struktura koalicji nad zbiorem graczy N jest zbiorem koalicji {C₁,…,C_k} takie, że:

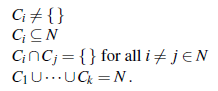
Na przykład, jeśli mamy N = {1,2,3}, to istnieje siedem możliwych koalicji:

{1}, {2}, {3}, {1,2},  {2,3} , {3,1}, i {1,2.3}

oraz pięć możliwych struktur koalicyjnych:

{{1}, {2}, {3}} , {{1}, {2,3}} , {{2}, {1,3}} , {{3}, {1,2}} , i {{1,2,3}}:

Używamy notacji CS(N) do oznaczenia zbioru wszystkich struktur koalicyjnych nad zbiorem gracza N, a CS(i) do oznaczenia koalicji, do której należy gracz i. Wynik gry jest określony przez wybory, jakich dokonują gracze, decydując, które koalicje mają utworzyć, oraz wybierając sposób podziału wartości v(C), którą otrzymuje każda koalicja. Formalnie, biorąc pod uwagę grę kooperacyjną określoną przez (N,v), wynikiem jest para (CS,x) składająca się ze struktury koalicyjnej i wektora wypłaty x = (x₁,…,x_n) gdzie x_i jest wartością trafia do gracza I. Wypłata musi spełniać warunek, zgodnie z którym każda koalicja C dzieli całą swoją wartość v(C) między swoich członków:

Na przykład, biorąc pod uwagę grę ({1,2,3},v), gdzie v({1})=4 i v({2,3})=10, możliwym wynikiem jest:

({{1} ,{2,3}} , (4;5;5)):

Oznacza to, że gracz 1 zostaje sam i akceptuje wartość 4, podczas gdy gracze 2 i 3 łączą siły, aby otrzymać wartość 10, którą wybierają równo. Niektóre gry kooperacyjne mają tę cechę, że gdy dwie koalicje łączą się ze sobą, nie radzą sobie gorzej, niż gdyby pozostały rozdzielone. Ta właściwość nazywana jest superaddytywnością. Formalnie gra jest superaddytywna, jeśli jej charakterystyczna funkcja spełnia następujący warunek:

Jeśli gra jest superaddytywna, wielka koalicja otrzymuje wartość co najmniej tak wysoką lub wyższą niż suma otrzymana przez jakąkolwiek inną strukturę koalicji. Jednak, jak wkrótce zobaczymy, gry superaddytywne nie zawsze kończą się wielką koalicją, z tego samego powodu, z którego gracze nie zawsze osiągają zbiorowo pożądany, optymalny w sensie Pareto wynik w dylemacie więźnia.