Aby zrozumieć POMDP, musimy najpierw je odpowiednio zdefiniować. POMDP ma te same elementy co MDP – model przejścia P (s’ | s , a), akcje A (s) i funkcja nagrody R (s,a,s’) – ale podobnie jak częściowo obserwowalne problemy wyszukiwania, ma również model czujnika P (e | s). Tutaj, podobnie jak w rozdziale 14, model czujnika określa prawdopodobieństwo dostrzeżenia dowodów w stanie s. Na przykład możemy przekształcić świat 4 x 3 w POMDP, dodając zaszumiony lub częściowy czujnik zamiast zakładać, że agent dokładnie zna swoją lokalizację. Można użyć zaszumionego czterobitowego czujnika, który zgłasza obecność lub brak ściany w każdym kierunku kompasu z dokładnością 1 – ε. Podobnie jak w przypadku MDP, możemy uzyskać zwartą reprezentację dla dużych POMDP, używając dynamicznych sieci decyzyjnych (patrz Rozdział 16.1.4). Dodajemy zmienne czujnika Et, zakładając, że zmienne stanu Xt mogą nie być bezpośrednio obserwowalne. Następnie podano model czujnika POMDP przez P (Et| Xt). Na przykład, możemy dodać zmienne czujnika do DDN na rysunku 16.4, takie jak BatteryMetert, aby oszacować rzeczywisty ładunek Batteryt i Speedometert, aby oszacować wielkość wektora prędkości ˙Xt. Czujnik sonaru Wallst może podać szacunkowe odległości do najbliższej ściany w każdym z czterech głównych kierunków względem aktualnej orientacji robota; wartości te zależą od aktualnej pozycji i orientacji Xt. W rozdziałach 4 i 11 zbadaliśmy niedeterministyczne i częściowo obserwowalne problemy planowania i zidentyfikowaliśmy stan przekonania – zbiór rzeczywistych stanów, w których może się znajdować agent – jako kluczową koncepcję do opisywania i obliczania rozwiązań. W POMDP stan przekonania b staje się rozkładem prawdopodobieństwa na wszystkie możliwe stany, tak jak w rozdziale 14. Na przykład początkowy stan przekonania dla POMDP 4 x 3 może być jednorodnym rozkładem na dziewięć stanów nieterminalnych wraz z zerami dla terminala stany, czyli częściowo obserwowalne problemy planowania i zidentyfikowaliśmy stan przekonania – zbiór rzeczywistych stanów, w których może się znajdować agent – jako kluczową koncepcję do opisywania i obliczania rozwiązań. W POMDP stan przekonania b staje się rozkładem prawdopodobieństwa na wszystkie możliwe stany, tak jak w rozdziale 14. Na przykład początkowy stan przekonania dla POMDP 4 x 3 może być jednorodnym rozkładem na dziewięć stanów nieterminalnych wraz z zerami dla terminala stany, czyli ![]()
Używamy notacji b (s), aby odnieść się do prawdopodobieństwa przypisanego do stanu faktycznego s przez stan przekonania b. Agent może obliczyć swój aktualny stan przekonań jako warunkowy rozkład prawdopodobieństwa w rzeczywistych stanach, biorąc pod uwagę dotychczasową sekwencję percepcji i działań. Jest to zasadniczo zadanie filtrowania opisane w rozdziale 14. Podstawowe równanie filtrowania rekurencyjnego (14.5 na stronie 485) pokazuje, jak obliczyć nowy stan przekonań na podstawie poprzedniego stanu przekonań i nowych dowodów. W przypadku POMDP również musimy rozważyć działanie, ale wynik jest zasadniczo taki sam. Jeśli b było poprzednim stanem przekonań, a agent wykonuje działanie a, a następnie postrzega dowód e, wtedy nowy stan przekonań uzyskuje się, obliczając prawdopodobieństwo przebywania w stanie s0 dla każdego s0 za pomocą następującego wzoru:
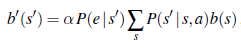
gdzie α jest stałą normalizującą, która sumuje stan przekonania do 1. Przez analogię do operatora aktualizacji do filtrowania , możemy zapisać to jako
![]()
W POMDP 4×3 załóżmy, że agent porusza się w lewo, a jego czujnik zgłasza jedną sąsiednią ścianę; wtedy jest całkiem prawdopodobne (choć nie jest to gwarantowane, ponieważ zarówno ruch, jak i czujnik są hałaśliwe), że agent jest teraz w (3,1). Ćwiczenie 16.POMD prosi o obliczenie dokładnych wartości prawdopodobieństwa dla nowego stanu przekonań. Podstawowy wgląd wymagany do zrozumienia POMDP jest następujący: optymalne działanie J zależy tylko od aktualnego stanu przekonania agenta. Oznacza to, że optymalną politykę można opisać poprzez mapowanie π*(b) stanów przekonań na działania. Nie zależy to od faktycznego stanu agenta. To dobrze, bo agent nie zna swojego aktualnego stanu; wszystko, co wie, to stan wiary. W związku z tym cykl decyzyjny agenta POMDP można podzielić na następujące trzy etapy:
- Mając aktualny stan przekonań b, wykonaj akcję a =π*(b).
- Obserwuj postrzeganie e
- Ustaw obecny stan przekonań na FoRWARD (b; a; e) i powtórz.
Możemy myśleć o POMDP jako wymagających przeszukiwania w przestrzeni stanów przekonań, podobnie jak metody rozwiązywania problemów bezczujnikowych i problemów losowych w Rozdziale 4. Główną różnicą jest to, że przestrzeń stanów przekonań POMDP jest ciągła, ponieważ stan przekonań POMDP jest prawdopodobieństwem. dystrybucja. Na przykład stan wiary dla świata 4 x 3 jest punktem w 11-wymiarowej ciągłej przestrzeni. Czynność zmienia stan przekonań, a nie tylko stan fizyczny, ponieważ wpływa na odbierane postrzeganie. W związku z tym działanie jest oceniane przynajmniej częściowo zgodnie z informacjami, które agent uzyskuje w wyniku. Dlatego POMDP uwzględniają wartość informacji (sekcja 15.6) jako jeden z elementów problemu decyzyjnego. Przyjrzyjmy się dokładniej wynikom działań. W szczególności obliczmy prawdopodobieństwo, że agent w stanie przekonań b osiągnie stan przekonań b’ po wykonaniu działania a. Teraz, gdybyśmy znali działanie i następujące po nim spostrzeżenie, to równanie (16.16) dostarczyłoby deterministycznej aktualizacji stanu przekonania: b’ = FORWARD (b , a , e). Oczywiście, kolejny percept nie jest jeszcze znany, więc agent może przybyć w jednym z kilku możliwych stanów przekonań b’, w zależności od perceptu, który jest odbierany. Prawdopodobieństwo dostrzeżenia e, zakładając, że a zostało wykonane w stanie przekonania b, jest określone przez zsumowanie wszystkich rzeczywistych stanów s’, które agent może osiągnąć:
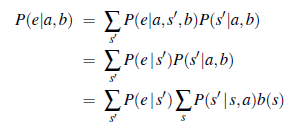
Zapiszmy prawdopodobieństwo osiągnięcia b’ z b przy danej akcji a, jako P (b’ |b, a). Prawdopodobieństwo to można obliczyć w następujący sposób:
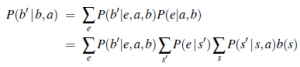
gdzie P (b’|e, a, b) wynosi 1, jeśli b’ = FORWARD (b, a, e) i 0 w przeciwnym razie. Równanie (16.17) można postrzegać jako definiujące model przejścia dla przestrzeni stan-przekonanie. Możemy również zdefiniować funkcję nagrody dla przejść stan-przekonanie, która jest wyprowadzona z oczekiwanej nagrody za przemiany stanu rzeczywistego, które mogą zachodzić. Tutaj używamy prostej formy (b; a), oczekiwanej nagrody, jeśli agent wykona stan przekonań b:
![]()
Razem P (b’ | b , a) i ρ(b , a) definiują obserwowalny MDP w przestrzeni stanów przekonań. Ponadto można wykazać, że optymalna polityka dla tego MDP, π*(b), jest również optymalna polityką I dla oryginalnego POMDP. Innymi słowy, rozwiązywanie POMDP w przestrzeni stanów fizycznych można zredukować do rozwiązywania MDP w odpowiedniej przestrzeni stanów przekonań. Fakt ten jest być może mniej zaskakujący, jeśli pamiętamy, że stan przekonań jest z definicji zawsze obserwowalny dla agenta