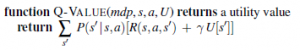Po ustaleniu, że użyteczność danej historii jest sumą zdyskontowanych nagród, możemy porównać polisy, porównując oczekiwane użyteczności uzyskane podczas ich realizacji. Zakładamy, że agent znajduje się w pewnym stanie początkowym s i definiujemy St (zmienną losową) jako stan, który agent osiąga w czasie t podczas wykonywania określonej polityki π. (Oczywiście, S0=s, stan, w którym znajduje się agent.) Rozkład prawdopodobieństwa na sekwencje stanów S1,S2, … jest określany przez stan początkowy, politykę π i model przejściowy dla środowiska. Oczekiwana użyteczność uzyskana przez wykonanie π startu w s jest dana wzorem

gdzie oczekiwanie E odnosi się do rozkładu prawdopodobieństwa w ciągach stanów określonych przez s i π . Teraz ze wszystkich polityk, które agent może wybrać do wykonania, zaczynając od s, jedna (lub więcej) będzie miała wyższe oczekiwane narzędzia niż wszystkie inne. Użyjemy π*s do oznaczenia jednej z tych zasad:
![]()
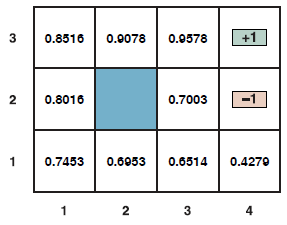
Pamiętaj, że π*s to polityka, więc zaleca działanie dla każdego stanu; jego związek z s w szczególności polega na tym, że jest to optymalna polityka, gdy s jest stanem początkowym. Niezwykłą konsekwencją stosowania zdyskontowanych narzędzi o nieskończonych horyzontach jest to, że optymalna polityka jest niezależna od stanu wyjściowego. (Oczywiście sekwencja działań nie będzie niezależna; pamiętaj, że polityka to funkcja określająca akcję dla każdego stanu.) Ten fakt wydaje się intuicyjnie oczywisty: jeśli polityka π*a jest optymalna, zaczynając od a polityka π*b jest optymalna, zaczynając od b, a następnie, gdy osiągną trzeci stan c, nie ma powodu, aby nie zgadzali się ze sobą lub z π*c , co dalej. Możemy więc po prostu napisać optymalną politykę. Biorąc pod uwagę tę definicję, prawdziwa użyteczność stanu to Uπ((s) – to znaczy oczekiwana suma zdyskontowanych nagród, jeśli agent realizuje optymalną politykę. Piszemy to jako U(s), pasując do notacji dla użyteczności wyniku. Rysunek przedstawia narzędzia dla świata 4 x 3 . Zauważ, że narzędzia są wyższe dla stanów bliżej wyjścia +1, ponieważ do wyjścia potrzeba mniej kroków.
Funkcja użyteczności U(s) pozwala agentowi wybrać działania zgodnie z zasadą maksymalnej oczekiwanej użyteczności, czyli wybrać działanie, które maksymalizuje nagrodę za kolejny krok plus oczekiwaną zdyskontowaną użyteczność kolejnego stanu:
![]()
Zdefiniowaliśmy użyteczność stanu, U(s), jako oczekiwaną sumę zdyskontowanych nagród od tego momentu. Z tego wynika, że istnieje bezpośredni związek między użytecznością państwa a użytecznością I jego sąsiadów: użyteczność państwa to oczekiwana nagroda za następne przejście plus zdyskontowana użyteczność następnego stanu, przy założeniu, że agent wybiera optymalne działanie. Oznacza to, że użyteczność stanu jest dana przez
![]()
Nazywa się to równaniem Bellmana, od Richarda Bellmana (1957). Użyteczności stanów — określone równaniem (jako oczekiwana użyteczność kolejnych ciągów stanów – są rozwiązaniami układu równań Bellmana. W rzeczywistości są to unikalne rozwiązania. Spójrzmy na jedno z równań Bellmana dla świata 4 x 3 . Wyrażenie na U(1;1) to
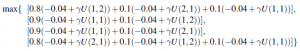
gdzie cztery wyrażenia odpowiadają ruchom w górę, w lewo, w dół i w prawo. Kiedy wstawiamy liczby z rysunku powyżej, przy ϒ=1, okazuje się, że najlepszym działaniem jest Up. Inną ważną wielkością jest funkcja użyteczności działania, czyli funkcja Q: Q(s,a) to oczekiwana użyteczność podjęcia danego działania w danym stanie. Funkcja Q jest związana z mediami w oczywisty sposób:
![]()
Ponadto optymalną politykę można wyodrębnić z funkcji Q w następujący sposób:
![]()
Możemy również opracować równanie Bellmana dla funkcji Q, zauważając, że oczekiwana całkowita nagroda za podjęcie działania jest jego natychmiastową nagrodą plus zdyskontowana użyteczność stanu końcowego, który z kolei może być wyrażony w postaci funkcji Q:
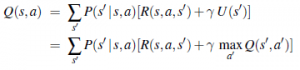
Rozwiązanie równań Bellmana dla U (lub dla Q) daje nam to, czego potrzebujemy, aby znaleźć optymalną politykę. Funkcja Q pojawia się raz za razem w algorytmach rozwiązywania MDP, więc zastosujemy następującą definicję: