W przykładzie MDP na rysunku wcześniejszym wydajność agenta była mierzona sumą nagród za doświadczane przejścia. Ten wybór miary wydajności nie jest arbitralny, ale nie jest jedyną możliwością dla funkcji użyteczności2 w historiach środowiska, które zapisujemy jako Uh([s0;a0; s1;a1,…, sn]). Pierwsze pytanie, na które należy odpowiedzieć, to czy istnieje horyzont skończony czy nieskończony dla podejmowania decyzji. Skończony horyzont oznacza, że istnieje ustalony czas N, po którym nic nie ma znaczenia — gra się, że tak powiem, skończona. Zatem,
dla wszystkich k > 0. Załóżmy na przykład, że agent zaczyna się w (3,1) w świecie 4 x 3 z rysunku i załóżmy, że N=3. Następnie, aby mieć jakąkolwiek szansę na osiągnięcie stanu +1, agent musi skierować się bezpośrednio w jego stronę, a optymalnym działaniem jest wejście w górę. Z drugiej strony, jeśli N=100, to jest mnóstwo czasu, aby obrać bezpieczną trasę, jadąc w lewo. Tak więc przy skończonym horyzoncie optymalne działanie w danym stanie może zależeć od tego, ile czasu pozostało. Polisa zależna od czasu nazywana jest niestacjonarną. Z drugiej strony bez ustalonego limitu czasowego nie ma powodu, aby zachowywać się inaczej w tym samym stanie w różnym czasie. Zatem optymalne działanie zależy tylko od aktualnego stanu, a optymalna polityka jest stacjonarna. Zasady dla przypadku o nieskończonym horyzoncie są zatem prostsze niż te dla przypadku o skończonym horyzoncie iw tym rozdziale zajmujemy się głównie przypadkiem o nieskończonym horyzoncie. (Później zobaczymy, że dla środowisk częściowo obserwowalnych, nieskończony horyzont przypadek nie jest taki prosty.) Zauważ, że „nieskończony horyzont” niekoniecznie oznacza, że wszystkie ciągi stanów są nieskończone; oznacza to tylko, że nie ma ustalonego terminu. W MDP o nieskończonym horyzoncie, który zawiera stan końcowy, mogą istnieć skończone sekwencje stanów. Kolejnym pytaniem, na które musimy się zdecydować, jest to, jak obliczyć użyteczność ciągów stanów. W tej części będziemy dodawać zniżkowe nagrody: użyteczność historii to
gdzie współczynnik dyskonta γ jest liczbą z zakresu od 0 do 1. Współczynnik dyskonta opisuje preferencje agenta dla bieżących nagród w stosunku do przyszłych nagród. Gdy γ zbliża się do zera, nagrody w odległej przyszłości są postrzegane jako nieistotne. Gdy γ zbliża się do 1, agent chętniej czeka na długoterminowe nagrody. Kiedy γ wynosi dokładnie 1, nagrody ze zniżką sprowadzają się do szczególnego przypadku nagród czysto addytywnych. Zauważ, że addytywność została użyta niejawnie w naszym użyciu funkcji kosztu ścieżki w heurystycznych algorytmach wyszukiwania.
Istnieje kilka powodów, dla których nagrody ze zniżką addytywną mają sens. Jedna jest empiryczna: wydaje się, że zarówno ludzie, jak i zwierzęta cenią sobie nagrody krótkoterminowe bardziej niż nagrody w odległej przyszłości. Inny jest ekonomiczny: jeśli nagrody są pieniężne, naprawdę lepiej jest je zdobyć wcześniej niż później, ponieważ wczesne nagrody można zainwestować i przynosić zwroty podczas oczekiwania na późniejsze nagrody. W tym kontekście współczynnik dyskontowy γ jest równoważny do stopy procentowej (1/γ -1. Na przykład współczynnik dyskontowy γ=0:9 odpowiada stopie procentowej 11,1%. Trzecim powodem jest niepewność co do prawdziwych nagród: mogą nigdy nie nadejść z różnych powodów, które nie są brane pod uwagę w modelu przejściowym. Przy pewnych założeniach współczynnik dyskontowy gamma jest równoznaczny z dodaniem prawdopodobieństwa 1-γ przypadkowego zakończenia w każdym kroku czasowym, niezależnie od podjętego działania. Czwarte uzasadnienie wynika z naturalnej właściwości preferencji w stosunku do historii. W terminologii wieloatrybutowej teorii użyteczności, każde przejścia 
może być postrzegany jako atrybut historii [s0,a0,s1,a1,s2…]. W zasadzie funkcja użyteczności może zależeć w dowolnie złożony sposób od tych atrybutów. Istnieje jednak wysoce prawdopodobne założenie, że preferencje są niezależne od preferencji, a mianowicie, że preferencje podmiotu między sekwencjami stanów są stacjonarne. Załóżmy dwie historie [s0;a0, s1,a1, s2,…] i [s’0;a’0; s’1;a’1 ; s’2,…] zaczynają się od tego samego przejścia (tj. s0=s’0, a0=a’0 i s1=s’1). Wtedy stacjonarność preferencji oznacza, że dwie historie powinny być uporządkowane według preferencji w taki sam sposób, jak historie [s1,a1, s2,…] i [s’1;a’1; s’0,…]. W języku polskim oznacza to, że jeśli wolisz jedną przyszłość od drugiej, która zaczyna się jutro, to i tak powinieneś preferować tę przyszłość, jeśli zamiast tego ma zaczynać się dzisiaj. Stacjonarność jest dość nieszkodliwym założeniem, ale dyskontowanie addytywne jest jedyną formą użyteczności na historiach, które go satysfakcjonują. Ostatecznym uzasadnieniem przecenionych nagród jest to, że dogodnie sprawia, że niektóre paskudne nieskończoności znikają. W przypadku horyzontów nieskończonych istnieje potencjalna trudność: jeśli środowisko nie zawiera stanu końcowego lub jeśli agent nigdy go nie osiągnie, wszystkie historie środowiska będą nieskończenie długie, a narzędzia z addytywnymi, niedyskontowalnymi nagrodami będą generalnie nieskończone. Chociaż możemy się zgodzić, że +∞ jest lepsze niż -∞, porównanie dwóch sekwencji stanów z użytecznością +∞ jest trudniejsze. Istnieją trzy rozwiązania, z których dwa już widzieliśmy:
1. Przy obniżonych nagrodach użyteczność nieskończonej sekwencji jest skończona. W rzeczywistości, jeśli γ < 1 i nagrody są ograniczone przez ±Rmax, mamy
używając standardowego wzoru na sumę nieskończonego szeregu geometrycznego.
- Jeśli środowisko zawiera stany końcowe i jeśli agent ma pewność, że w końcu osiągnie jeden, nigdy nie będziemy musieli porównywać nieskończonych sekwencji. Polityka, która gwarantuje osiągnięcie stanu końcowego, nazywana jest polityką właściwą. Przy odpowiednich zasadach możemy użyć γ=1 (tj. dodatkowych nagród bez rabatu). Pierwsze trzy zasady przedstawione na rysunku (b) są prawidłowe, ale czwarta jest niewłaściwa.
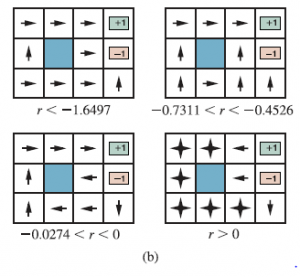
Zyskuje nieskończoną całkowitą nagrodę, pozostając z dala od stanów końcowych, gdy nagroda za przejścia między stanami nieterminalnymi jest dodatnia. Istnienie niewłaściwych zasad może spowodować, że standardowe algorytmy rozwiązywania problemów MDP zakończą się niepowodzeniem z dodatkowymi nagrodami, a zatem stanowi dobry powód do korzystania ze zdyskontowanych nagród.
- Nieskończone sekwencje mogą być porównywane pod względem średniej nagrody uzyskanej na czas kroku Średnia nagroda. Załóżmy, że przejścia do kwadratu (1,1) w świecie 4 x 3 mają nagrodę 0,1, podczas gdy przejścia do innych stanów nieterminalnych mają nagrodę 0,01. Wtedy polisa, która stara się pozostać w (1,1), będzie miała wyższą średnią nagrodę niż polisa, która zostaje gdzie indziej. Średnia nagroda jest użytecznym kryterium dla niektórych problemów, ale analiza algorytmów średniej nagrody jest złożona.
Nagrody ze zniżką addytywną stanowią najmniej trudności w ocenie historii, więc odtąd będziemy z nich korzystać.