Fakt, że wartość sekwencji obserwacji jest niezmienna w przypadku permutacji sekwencji, jest intrygujący, ale sam w sobie nie prowadzi do wydajnych algorytmów do optymalnego gromadzenia informacji. Nawet jeśli ograniczymy się do wcześniejszego wybrania ustalonego podzbioru obserwacji do zebrania, istnieje 2n możliwych takich podzbiorów z n potencjalnych obserwacji. W ogólnym przypadku mamy do czynienia z jeszcze bardziej złożonym problemem znalezienia optymalnego planu warunkowego, który wybiera obserwację, a następnie działa lub wybiera więcej obserwacji, w zależności od wyniku. Takie plany tworzą drzewa, a liczba takich drzew jest superwykładnicza w n. W przypadku obserwacji zmiennych w sieci decyzyjnej okazuje się, że problem ten jest nierozwiązywalny nawet wtedy, gdy sieć jest wielodrzewa. Istnieją jednak szczególne przypadki, w których problem można skutecznie rozwiązać. Tutaj przedstawiamy jeden taki przypadek: problem poszukiwania skarbów (lub najmniej kosztowna sekwencja testowa, dla mniej romantycznych). Jest n lokalizacji 1,…,n; każda lokalizacja i zawiera skarb z niezależnym prawdopodobieństwem P(i); a sprawdzenie lokalizacji i kosztuje C(i). Odpowiada to sieci decyzyjnej, w której wszystkie potencjalne zmienne dowodowe Treasurei są całkowicie niezależne. Agent bada lokalizacje w określonej kolejności, dopóki nie znajdzie skarbu; pytanie brzmi, jaka jest optymalna kolejność? Aby odpowiedzieć na to pytanie, będziemy musieli rozważyć oczekiwane koszty i prawdopodobieństwa powodzenia różnych sekwencji obserwacji, zakładając, że agent zatrzymuje się po znalezieniu skarbu. Niech x będzie takim ciągiem; xy być konkatenacją ciągów x i y; C(x) będzie oczekiwanym kosztem x; P(x) jest prawdopodobieństwem, że sekwencja x zdoła znaleźć skarb a F(x)=1-P(x) jest prawdopodobieństwem niepowodzenia. Biorąc pod uwagę te definicje, mamy
![]()
oznacza to, że ciąg xy na pewno poniesie koszt x, a jeśli x zawiedzie, poniesie również koszt y. Podstawową ideą w każdym zadaniu optymalizacji sekwencji jest przyjrzenie się zmianie kosztu, zdefiniowanej przez Δ=C(wxyz)-C(wyxz), gdy dwa sąsiednie podciągi x i y w ogólnej sekwencji wxyz są odwrócone. Gdy sekwencja jest optymalna, wszystkie takie zmiany pogarszają sekwencję. Pierwszym krokiem jest pokazanie, że znak efektu (zwiększenie lub zmniejszenie kosztu) nie zależy od kontekstu dostarczonego przez w i z. Mamy
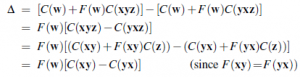
Pokazaliśmy więc, że kierunek zmiany kosztu całej sekwencji zależy tylko od kierunku zmiany kosztu odwróconej pary elementów; kontekst pary nie ma znaczenia. Daje nam to możliwość sortowania sekwencji przez porównania parami w celu uzyskania optymalnego rozwiązania. W szczególności mamy teraz
![]()
Odnosi się to do dowolnych sekwencji x i y, więc dotyczy to szczególnie, gdy x i y są pojedynczymi obserwacjami lokalizacji odpowiednio i oraz j. Wiemy więc, że aby i oraz j sąsiadowały w optymalnej sekwencji, musimy mieć C(i)P(j) ≤ C(j)P(i) lub P(i)/C(i) ≥ P(j)/C(j). Innymi słowy, optymalna kolejność szereguje lokalizacje zgodnie z prawdopodobieństwem sukcesu na koszt jednostkowy.