Na te pytania można odpowiedzieć, wypisując pewne ograniczenia preferencji, jakie powinien mieć racjonalny podmiot, a następnie pokazując, że zasadę MEU można wyprowadzić z ograniczeń. Do opisu preferencji agenta używamy następującej notacji:
![]()
Teraz oczywistym pytaniem jest, jakie rodzaje rzeczy to A i B? Mogą to być stany świata, ale najczęściej nie ma pewności co do tego, co tak naprawdę jest oferowane. Na przykład pasażer linii lotniczej, któremu proponuje się „danie z makaronu lub kurczaka”, nie wie, co kryje się pod folią aluminiową1. Makaron może być pyszny lub zakrzepły, a kurczak soczysty lub rozgotowany nie do poznania. Możemy myśleć o zestawie wyników dla każdej akcji jak o loterii – myśleć o każdej akcji jak o losie. Loteria L z możliwymi wynikami S1,…,Sn, które występują z prawdopodobieństwami p1,…, pn jest zapisane
![]()
Ogólnie rzecz biorąc, każdy wynik Si loterii może być stanem atomowym lub inną loterią. Podstawowym problemem teorii użyteczności jest zrozumienie, w jaki sposób preferencje między złożonymi loteriami są powiązane z preferencjami między podstawowymi stanami w tych loteriach. Aby rozwiązać ten problem, wymieniamy sześć ograniczeń, których przestrzegania wymagamy od jakiejkolwiek rozsądnej relacji preferencji:
* Porządność: Biorąc pod uwagę dowolne dwie loterie, racjonalny agent musi albo preferować jedną, albo ocenić je jako równie preferowane. Oznacza to, że agent nie może uniknąć decyzji. Jak wspomniano na stronie 412, odmowa obstawienia jest jak odmowa pozostawienia czasu na upływ.
Dokładnie jeden z (A ≻ B); (B ≻ A); lub (A ∼ B) trzyma
* Przechodniość: biorąc pod uwagę dowolne trzy loterie, jeśli agent woli A do B i B do C, to agent musi preferować A do C.
(A ≻ B)Λ(B ≻ C) ) ⇒ (A ≻ C)
* Ciągłość: Jeśli jakaś loteria B jest pomiędzy A i C, to istnieje pewne prawdopodobieństwo p, dla którego racjonalny agent będzie obojętny między otrzymaniem B na pewno, a loterią, która daje A z prawdopodobieństwem p i C z prawdopodobieństwem 1- p .
A ≻ B v C ∃p [p;A; 1- p,C] ∼ B:
* Zastępowalność: jeśli agent jest obojętny w przypadku dwóch loterii A i B, to agent jest obojętny w przypadku dwóch bardziej złożonych loterii, które są takie same, z wyjątkiem tego, że B zastępuje A w jednej z nich. Zasada ta obowiązuje niezależnie od prawdopodobieństw i innych wyników loterii.
(A ∼ B) ⇒ [p,A 1- p,C] ∼ [p,B;1- p,C] :
Odnosi się to również, jeśli podstawimy w tym aksjomacie.
* Monotoniczność: Załóżmy, że dwie loterie mają te same dwa możliwe wyniki, A i B. Jeśli agent woli A do B, to agent musi preferować loterię, która ma większe prawdopodobieństwo dla A (i odwrotnie).
(A ≻ B ) ⇒ (p > q , [p,A; 1 – p;B] [q,A; 1-q;B])
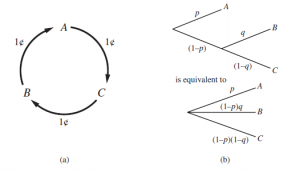
* Rozkład: loterie złożone można zredukować do prostszych za pomocą praw prawdopodobieństwa. Nazywa się to zasadą „żadnej zabawy w hazardzie”: jak pokazuje rysunek 15.1(b), łączy ona dwie następujące po sobie loterie w jedną równoważną loterię.
[p,A; 1-p; [q,B; 1-q,C]] ∼ [p;A; (1-p)q,B; (1-p)(1-q);C]
Te ograniczenia są znane jako aksjomaty teorii użyteczności. Każdy aksjomat może być motywowany przez pokazanie, że podmiot, który go narusza, w pewnych sytuacjach będzie wykazywał jawnie irracjonalne zachowanie. Na przykład możemy motywować przechodniość, sprawiając, że agent o nieprzechodnich preferencjach daje nam wszystkie swoje pieniądze. Załóżmy, że agent ma nieprzechodnie preferencje A ≻ B ≻ C ≻ A, gdzie A, B i C to dobra, które można swobodnie wymieniać. Jeśli agent ma obecnie A, możemy zaproponować wymianę C na A plus jeden cent. Agent preferuje C, więc byłby skłonny dokonać tej wymiany. Moglibyśmy wtedy zaproponować wymianę B na C, wydobycie kolejnego centa, a na koniec wymianę A na B. To prowadzi nas z powrotem do punktu wyjścia, z wyjątkiem tego, że agent dał nam trzy centy (rysunek (a)). Możemy kontynuować cykl, dopóki agent w ogóle nie będzie miał pieniędzy. Najwyraźniej agent działał w tym przypadku irracjonalnie.