Po naszkicowaniu kilku pomysłów na przedstawienie złożonych procesów jako DBN, przechodzimy teraz do kwestii wnioskowania. W pewnym sensie na to pytanie już udzielono odpowiedzi: dynamiczne sieci bayesowskie są sieciami bayesowskimi i mamy już algorytmy wnioskowania w sieciach bayesowskich. Mając sekwencję obserwacji, można skonstruować pełną reprezentację DBN w sieci bayesowskiej, replikując wycinki, aż sieć będzie wystarczająco duża, aby pomieścić obserwacje, jak na rysunku
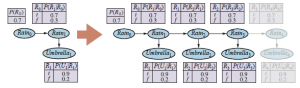
Ta technika nazywa się rozwijaniem. (Z technicznego punktu widzenia DBN jest równoważny pół-nieskończonej sieci uzyskanej przez rozwijanie na zawsze. Wycinki dodane poza ostatnią obserwacją nie mają wpływu na wnioskowanie w okresie obserwacji i można je pominąć.) Po rozwinięciu DBN można użyć dowolnego z algorytmy wnioskowania – eliminacja zmiennych, metody grupowania itd. Niestety naiwne zastosowanie rozwijania nie byłoby szczególnie wydajne. Jeśli chcemy przeprowadzić filtrowanie lub wygładzanie z długą sekwencją obserwacji e1:t , rozwinięta sieć wymagałaby przestrzeni O(t) i tym samym rosłaby bez ograniczeń w miarę dodawania kolejnych obserwacji. Co więcej, jeśli po prostu uruchomimy algorytm wnioskowania od nowa za każdym razem, gdy dodana zostanie obserwacja, czas wnioskowania na aktualizację również wzrośnie jako O(t). Patrząc wstecz, widzimy, że stały czas i przestrzeń na aktualizację filtrowania można osiągnąć, jeśli obliczenia można wykonać rekurencyjnie. Zasadniczo aktualizacja filtrowania w równaniu polega na zsumowaniu zmiennych stanu z poprzedniego kroku czasowego w celu uzyskania rozkładu dla nowego kroku czasowego. Sumowanie zmiennych jest dokładnie tym, co robi algorytm eliminacji zmiennych i okazuje się, że uruchamianie eliminacji zmiennych ze zmiennymi w kolejności czasowej dokładnie naśladuje operację aktualizacji filtrowania rekurencyjnego w równaniu. Zmodyfikowany algorytm utrzymuje większość dwóch wycinków w pamięci w dowolnym momencie: zaczynając od wycinka 0, dodajemy wycinek 1, następnie sumujemy wycinek 0, następnie dodajemy wycinek 2, a następnie sumujemy wycinek 1 i tak dalej. W ten sposób możemy osiągnąć stałą przestrzeń i czas na aktualizację filtrowania. (Taką samą wydajność można osiągnąć poprzez odpowiednie modyfikacje algorytmu klastrowania.). Tyle dobrych wieści; teraz złe wieści: okazuje się, że „stała” złożoności czasowej i przestrzennej aktualizacji jest prawie we wszystkich przypadkach wykładnicza liczby zmiennych stanu. Dzieje się tak, że w miarę postępu eliminacji zmiennych czynniki rosną i obejmują wszystkie zmienne stanu (a dokładniej wszystkie te zmienne stanu, które mają rodziców w poprzednim przedziale czasu). Maksymalny rozmiar czynnika to O(dn+k), a całkowity koszt aktualizacji na krok to O(ndn+k), gdzie d to rozmiar domeny zmiennych, a k to maksymalna liczba rodziców dowolnej zmiennej stanu. Oczywiście jest to znacznie mniej niż koszt aktualizacji HMM, który wynosi O(d2n), ale nadal jest niewykonalny dla dużej liczby zmiennych. Ten ponury fakt oznacza, że chociaż możemy używać DBN do reprezentowania bardzo złożonych procesów czasowych z wieloma słabo powiązanymi zmiennymi, nie możemy skutecznie i dokładnie wnioskować o tych procesach. Sam model DBN, który reprezentuje wcześniejszy wspólny rozkład na wszystkie zmienne, jest rozkładany na czynniki składowe CPT, ale rozkład tylnego stawu uwarunkowany sekwencją obserwacji – to znaczy przekazem do przodu – generalnie nie podlega rozkładowi. Problem jest generalnie nierozwiązywalny, więc musimy sięgnąć do metod przybliżonych.