Przykład stomatologii ilustruje powszechnie występujący wzorzec, w którym pojedyncza przyczyna bezpośrednio wpływa na szereg skutków, z których wszystkie są warunkowo niezależne od przyczyny. Pełny wspólny rozkład można zapisać jako
![]()
Taki rozkład prawdopodobieństwa nazywany jest naiwnym modelem Bayesa – „naiwnym”, ponieważ jest często stosowany (jako założenie upraszczające) w przypadkach, gdy zmienne „skutków” nie są ściśle niezależne ze względu na zmienną przyczyny. (Naiwny model Bayesa jest czasami nazywany klasyfikatorem bayesowskim, co skłoniło prawdziwych Bayesa do nazwania go idiotycznym modelem Bayesa). W praktyce naiwne systemy Bayesa często działają bardzo dobrze, nawet jeśli założenie warunkowej niezależności nie jest ściśle prawda. Aby użyć naiwnego modelu Bayesa, możemy zastosować równanie, aby uzyskać prawdopodobieństwo przyczyny przy pewnych zaobserwowanych efektach. Zaobserwowane efekty nazwijmy E = e , podczas gdy pozostałe zmienne efektu Y są nieobserwowane. Następnie można zastosować standardową metodę wnioskowania z rozkładu łącznego :
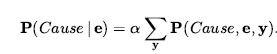
Następnie otrzymujemy
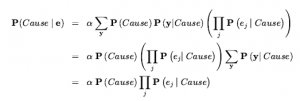
gdzie następuje ostatni wiersz, ponieważ suma nad y wynosi 1. Reinterpretacja tego równania słowami: dla każdej możliwej przyczyny pomnóż prawdopodobieństwo a priori przyczyny przez iloczyn prawdopodobieństw warunkowych zaobserwowanych skutków danej przyczyny; następnie znormalizuj wynik. Czas wykonania tego obliczenia jest liniowy pod względem liczby zaobserwowanych efektów i nie zależy od liczby nieobserwowanych efektów (która może być bardzo duża w dziedzinach takich jak medycyna). W następnym rozdziale zobaczymy, że jest to powszechne zjawisko we wnioskowaniu probabilistycznym: zmienne dowodowe, których wartości są nieobserwowane, zwykle „znikają” z obliczeń.