Zarówno w naukowych, jak i zdroworozsądkowych teoriach świata przedmioty mają wysokość, masę, koszt i tak dalej. Wartości, które przypisujemy tym właściwościom, nazywamy miarami. Zwykłe miary ilościowe są dość łatwe do przedstawienia. Wyobrażamy sobie, że wszechświat zawiera abstrakcyjne „obiekty pomiarowe”, takie jak długość, która jest długością tego odcinka linii:|—————————-| . Możemy nazwać tę długość 1,5 cala lub 3,81 centymetra. Tak więc ta sama długość ma różne nazwy w naszym języku. Reprezentujemy długość za pomocą funkcji jednostek, która jako argument przyjmuje liczbę.
Naturalne rodzaje
Niektóre kategorie mają ścisłe definicje: obiekt jest trójkątem wtedy i tylko wtedy, gdy jest wielokątem o trzech bokach. Z drugiej strony większość kategorii w świecie rzeczywistym nie ma jednoznacznej definicji; są to tak zwane kategorie rodzaju naturalnego. Na przykład pomidory wydają się być matowe, szkarłatne; z grubsza kulisty; z wcięciem u góry w miejscu łodygi; około dwóch do czterech cali średnicy; o cienkiej, ale twardej skórze; oraz z miąższem, nasionami i sokiem w środku. Istnieje jednak zróżnicowanie: niektóre pomidory są żółte lub pomarańczowe, niedojrzałe pomidory są zielone, niektóre są mniejsze lub większe niż przeciętne, a pomidorki koktajlowe są jednakowo małe. Zamiast mieć pełną definicję pomidorów, mamy zestaw funkcji, które służą do identyfikacji obiektów, które są wyraźnie typowymi pomidorami, ale mogą nie identyfikować ostatecznie innych obiektów. (Czy może istnieć pomidor, który jest puszysty jak brzoskwinia?) Stanowi to problem dla agenta logicznego. Agent nie może być pewien, że postrzegany przez niego przedmiot jest pomidorem, a nawet gdyby był pewien, nie mógłby być pewien, jakie właściwości ma ten typowy pomidor. Ten problem jest nieuniknioną konsekwencją działania w częściowo obserwowalnych środowiskach. Jednym z przydatnych podejść jest oddzielenie tego, co jest prawdziwe we wszystkich przypadkach kategorii, od tego, co jest prawdziwe tylko w przypadku typowych przypadków. Tak więc oprócz kategorii Pomidory będziemy mieli również kategorię Typowe (Pomidory). Tutaj funkcja Typowa odwzorowuje kategorię na podklasę, która zawiera tylko typowe instancje:
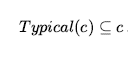
Większość wiedzy o naturalnych gatunkach dotyczy ich typowych przypadków:
![]()
W ten sposób możemy zapisywać przydatne fakty dotyczące kategorii bez dokładnych definicji. Trudność w dostarczeniu dokładnych definicji dla większości kategorii naturalnych została dogłębnie wyjaśniona przez Wittgensteina (1953). Posłużył się przykładem gier, aby pokazać, że członkowie kategorii mają wspólne „podobieństwa rodzinne”, a nie konieczne i wystarczające cechy: jaka ścisła definicja obejmuje szachy, berka, pasjansa i zbijaka? Użyteczność pojęcia ścisłej definicji zakwestionował także Quine. Wskazał, że nawet definicja „kawalera” jako niezamężnego dorosłego mężczyzny jest podejrzana; można na przykład zakwestionować stwierdzenie w rodzaju „Papież jest kawalerem”. Chociaż nie jest to całkowicie fałszywe, to użycie jest z pewnością niefortunne, ponieważ wywołuje niezamierzone wnioski ze strony słuchacza. Napięcie można by chyba rozwiązać, rozróżniając definicje logiczne odpowiednie do wewnętrznej reprezentacji wiedzy od bardziej zniuansowanych kryteriów szczęśliwego użycia językowego. To ostatnie można osiągnąć poprzez „filtrowanie” twierdzeń wywodzących się z tego pierwszego. Możliwe jest również, że błędy w użyciu językowym służą jako informacja zwrotna do modyfikacji wewnętrznych definicji, tak że filtrowanie staje się niepotrzebne. Jeśli odcinek linii nazywa się L1, możemy napisać
![]()
Konwersja między jednostkami odbywa się poprzez porównanie wielokrotności jednej jednostki do drugiej:
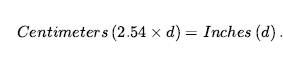
Podobne aksjomaty można zapisać dla funtów i kilogramów, sekund i dni oraz dolarów i centów. Miary mogą być używane do opisu obiektów w następujący sposób:
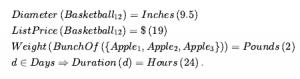
Zauważ, że $(1) nie jest dolarem — to cena. Można mieć dwa banknoty dolarowe, ale istnieje tylko jeden obiekt o nazwie $(1) . Zauważ również, że chociaż cale(0) i centymetry(0) odnoszą się do tej samej zerowej długości, nie są one identyczne z innymi zerowymi miarami, takimi jak sekundy(0). Proste, ilościowe miary są łatwe do przedstawienia. Inne miary stanowią większy problem, ponieważ nie mają uzgodnionej skali wartości. Ćwiczenia mają trudności, desery mają smakowitość, a wiersze piękno, ale tym walorom nie można przypisać liczb. Można by w chwili czystej księgowości odrzucić takie właściwości jako bezużyteczne dla celów logicznego rozumowania; lub, co gorsza, próbować narzucić pięknu skalę liczbową. Byłby to poważny błąd, ponieważ jest niepotrzebny. Najważniejszym aspektem miar nie są poszczególne wartości liczbowe, ale możliwość uporządkowania miar. Chociaż miary nie są liczbami, nadal możemy je porównywać, używając symbolu porządkowania, takiego jak . Na przykład możemy uwierzyć, że ćwiczenia Norviga są trudniejsze niż ćwiczenia Russella i że trudniejsze ćwiczenia mają mniej punktów:
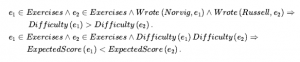
To wystarczy, aby zdecydować, które ćwiczenia wykonać, mimo że nigdy nie używano wartości liczbowych trudności. (Trzeba jednak odkryć, kto napisał które ćwiczenia). Tego rodzaju monotoniczne relacje między miarami stanowią podstawę dziedziny fizyki jakościowej, poddziedziny sztucznej inteligencji, która bada, jak wnioskować o układach fizycznych bez zagłębiania się w szczegółowe równania i symulacje numeryczne. Fizyka jakościowa jest omówiona w dziale notatek historycznych.