Żadna z metod wnioskowania opisanych do tej pory w tym rozdziale nie poradzi sobie z twierdzeniem postaci x = y bez dodatkowej pracy. Można zastosować trzy różne podejścia. Pierwszym z nich jest aksjomatyzacja równości – zapisanie zdań o relacji równości w bazy wiedzy. Musimy powiedzieć, że równość jest zwrotna, symetryczna i przechodnia, a także musimy powiedzieć, że możemy zastąpić równaniami równymi w dowolnym predykacie lub funkcji. Potrzebujemy więc trzech podstawowych aksjomatów, a następnie po jednym dla każdego predykatu i funkcji:
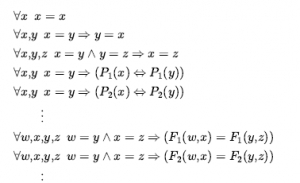
Biorąc pod uwagę te zdania, standardowa procedura wnioskowania, taka jak rozdzielczość, może wykonywać zadania wymagające wnioskowania o równości, takie jak rozwiązywanie równań matematycznych. Jednak te aksjomaty wygenerują wiele wniosków, z których większość nie będzie pomocna w dowodzie. Tak więc drugie podejście polega na dodawaniu reguł wnioskowania, a nie aksjomatów. Najprostsza zasada, demodulacja, przyjmuje klauzulę jednostkową x = y i pewną klauzulę α który zawiera termin x i daje nową klauzulę utworzoną przez podstawienie y za x w obrębie α. Działa, jeśli termin w α łączy się z ; nie musi być dokładnie równe x. Zauważ, że demodulacja jest kierunkowa; biorąc pod uwagę x = y , x zawsze jest zastępowany przez y, nigdy odwrotnie. Oznacza to, że demodulację można wykorzystać do uproszczenia wyrażeń za pomocą demodulatorów, takich jak z+0 = z lub z1 = z . Jako inny przykład podano
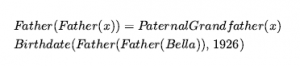
możemy zakończyć demodulacją
![]()
Bardziej formalnie mamy
* DEMODULACJA: Dla dowolnych terminów x, y i z, gdzie z pojawia się gdzieś w dosłownym m i gdzie UNIFY(x,z) = θ
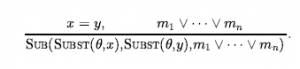
gdzie SUBST jest zwykłym podstawieniem listy wiążącej, a SUB(x,y,m) oznacza zastąpienie x przez y gdzieś w obrębie m . Reguła może być również rozszerzona o obsługę klauzul niejednostkowych, w których pojawia się znak równości:
* PARAMODULACJA: dla dowolnych wyrażeń x, y i z , gdzie występuje gdzieś w literze m , a gdzie , UNIFY(x,z) = θ

Na przykład z
![]()
mamy θ = UNIFY(F(A,y),F(x,B)) = {x/A , y/B} , i możemy zakończyć przez paramodulację zdania
![]()
Paramodulacja daje pełną procedurę wnioskowania dla logiki pierwszego rzędu z równością. Trzecie podejście obsługuje wnioskowanie o równości w całości w ramach rozszerzonego algorytmu unifikacji. Oznacza to, że terminy są unifikowalne, jeśli są równorzędne do udowodnienia przy pewnym podstawieniu, gdzie „dowieść” pozwala na wnioskowanie o równości. Na przykład terminy 1 + 2 i 2 + 1 zwykle nie są unifikowalne, ale algorytm unifikacji, który wie, że x + y = y + x może je ujednolicić za pomocą pustego podstawienia. Tego rodzaju unifikację równań można przeprowadzić za pomocą wydajnych algorytmów zaprojektowanych dla poszczególnych używanych aksjomatów (przemienność, asocjatywność itd.), a nie poprzez jawne wnioskowanie z tymi aksjomatami. Dowodzące twierdzeń przy użyciu tej techniki są ściśle związane z systemami CLP.