Ta sekcja zawiera dowód kompletności rozwiązania. Może być bezpiecznie pominięty przez tych, którzy są gotowi przyjąć ją na wiarę. Pokazujemy, że rozwiązanie jest obalające zupełne, co oznacza, że jeśli zbiór zdań jest niezadowalający, to rozwiązanie zawsze będzie w stanie wyprowadzić sprzeczność. Rozdzielczość nie może być użyta do wygenerowania wszystkich logicznych konsekwencji zbioru zdań, ale może być użyta do ustalenia, że dane zdanie jest zawarte w zbiorze zdań. Można go zatem wykorzystać do znalezienia wszystkich odpowiedzi na zadane pytanie Q(x) , udowadniając, że KB Λ ¬Q(x) jest ono niezadowalające.
Przyjmujemy, że każde zdanie w logice pierwszego rzędu (bez równości) może zostać przepisane jako zbiór klauzul w CNF. Można to udowodnić przez indukcję na formie zdania, używając zdań atomowych jako przypadku bazowego. Naszym celem jest zatem udowodnienie, co następuje: jeśli S jest to niespełniony zbiór klauzul, to zastosowanie skończonej liczby kroków rozstrzygnięcia do S przyniesie sprzeczność.
Nasz szkic dowodowy podąża za oryginalnym dowodem Robinsona z pewnymi uproszczeniami zaczerpniętymi z Genesereth i Nilsson. Podstawowa struktura dowodu jest następująca:

- Po pierwsze, zauważamy, że jeśli S jest niespełniony, to istnieje określony zbiór podstawowych wystąpień zdań S o takim charakterze, że ten zbiór również jest niespełniony (twierdzenie Herbranda).
- Następnie odwołujemy się do twierdzenia o rozstrzygnięciu w podstawie podanego w rozdziale 7, które stwierdza, że rozstrzyganie zdaniowe jest kompletne dla zdań gruntowych.
- Następnie używamy lematu unoszącego, aby pokazać, że dla każdego dowodu rozstrzygnięcia zdań przy użyciu zbioru zdań podstawowych istnieje odpowiedni dowód rozstrzygnięcia pierwszego rzędu wykorzystujący zdania pierwszego rzędu, z których otrzymano zdania podstawowe.
Aby wykonać pierwszy krok, potrzebujemy trzech nowych koncepcji:
* HERBRAND UNIVERSE: Jeśli S jest zbiorem klauzul, to HS , uniwersum Herbranda S , jest zbiorem wszystkich podstawowych terminów, które można skonstruować z następującego:
- Symbole funkcji w S , jeśli istnieją.
- Symbole stałe w S , jeśli istnieją; jeśli brak, to domyślny symbol stałej, S.
Na przykład, jeśli S zawiera tylko zdanie ![]() to HS jest następującym nieskończonym zbiorem terminów podstawowych:
to HS jest następującym nieskończonym zbiorem terminów podstawowych:
{A,B,F(A,A),F(A,B),F(B,A),F(B,B),F(A,F(A,A)),…}.
* NASYCENIE: Jeśli S jest zbiorem klauzul i P jest zbiorem warunków podstawowych, to P(S) , nasycenie S względem P , jest zbiorem wszystkich klauzul podstawowych uzyskanych przez zastosowanie wszystkich możliwych zgodnych podstawień warunków podstawowych w P dla zmiennych w S .
* BAZA HERBRAND: Nasycenie zbioru klauzul S w odniesieniu do jego uniwersum Herbranda nosi nazwę bazy Herbrand , pisanej jako HS(S) . Na przykład, jeśli S zawiera wyłącznie klauzulę podaną powyżej, to HS(S) jest nieskończonym zbiorem klauzul
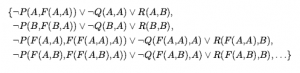
Definicje te pozwalają na sformułowanie formy twierdzenia Herbranda (Herbrand, 1930):
Jeśli zbiór klauzul jest niespełniony, to istnieje skończony podzbiór HS(S), który również jest niespełniony.
Niech S’ będzie tym skończonym podzbiorem zdań podstawowych. Teraz możemy odwołać się do twierdzenia o rozdzielczości podstawowej (strona 228), aby pokazać, że zamknięcie rozdzielczości RC(S’) zawiera pustą klauzulę. Oznacza to, że uruchomienie rozwiązania zdań do zakończenia na S” wyprowadzi sprzeczność.
Teraz, gdy ustaliliśmy, że zawsze istnieje dowód rozdzielczości obejmujący jakiś skończony podzbiór bazy Herbranda z , następnym krokiem jest wykazanie, że istnieje dowód rozdzielczości wykorzystujący klauzule samego S, które niekoniecznie są klauzulami podstawowymi. Zaczynamy od rozważenia pojedynczego zastosowania zasady resolution. Robinson stwierdził ten lemat:
Niech C1 i C2 będą dwoma klauzulami bez wspólnych zmiennych, a C1′ i C2′ będą podstawowymi instancjami C1 i C2 . Jeśli C’ jest rezolwentą C1′ i C2′ , to istnieje klauzula C taka, że (1) C jest rezolwentą C1 i C2 oraz (2) C’ jest podstawową instancją C.
Nazywa się to lematem znoszącym, ponieważ przenosi krok dowodowy z klauzul podstawowych do ogólnych klauzul pierwszego rzędu. Aby udowodnić swój podstawowy lemat podnoszenia, Robinson musiał wymyślić unifikację i wyprowadzić wszystkie właściwości większości ogólnych unifikatorów. Zamiast powtarzać tutaj dowód, po prostu zilustrujemy lemat:
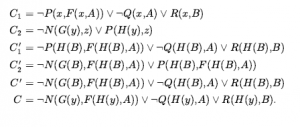
Widzimy, że rzeczywiście C’ jest podstawową instancją C . Ogólnie, aby C1’i C2′ miały jakiekolwiek rezolwenty, muszą być skonstruowane przez zastosowanie najpierw do C1 i C2 najbardziej ogólnego unifikatora pary komplementarnych literałów w C1 i C2 . Z lematu o podnoszeniu łatwo wyprowadzić podobne stwierdzenie o dowolnej kolejności zastosowań reguły rozstrzygania:
Dla każdej klauzuli C’ w zamknięciu rezolucji S’ istnieje klauzula C w zamknięciu rezolucji S taka, że C’ jest podstawową instancją C, a wyprowadzenie C ma taką samą długość jak wyprowadzenie C’.
Z tego faktu wynika, że jeżeli klauzula pusta pojawia się w zamknięciu rezolucji S’ , to musi ona również pojawić się w zamknięciu rezolucji S . Dzieje się tak, ponieważ pusta klauzula nie może być podstawową instancją żadnej innej klauzuli. Reasumując: pokazaliśmy, że jeśli S jest niespełnialne, to istnieje skończone wyprowadzenie pustej klauzuli za pomocą reguły rozwiązywania. Zniesienie dowodzenia twierdzeń z klauzul podstawowych do klauzul pierwszego rzędu zapewnia ogromny wzrost mocy. Ten wzrost wynika z faktu, że dowód pierwszego rzędu wymaga zmiennych instancji tylko w takim stopniu, w jakim jest to konieczne dla dowodu, podczas gdy metody klauzul podstawowych były wymagane do zbadania ogromnej liczby arbitralnych instancji.