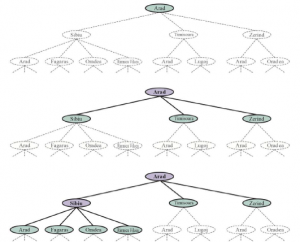
Drzewo wyszukiwania pokazane na rysunku (na dole) zawiera ścieżkę z Arad do Sibiu iz powrotem do Arad. Mówimy, że Arad jest powtarzającym się stanem w drzewie wyszukiwania, generowanym w tym przypadku przez cykl (znany również jako ścieżka zapętlona). Tak więc, mimo że przestrzeń stanów ma tylko 20 stanów, pełne drzewo poszukiwań jest nieskończone, ponieważ nie ma ograniczeń co do częstotliwości przechodzenia przez pętlę.
Po drugie, nie możemy się martwić o powtórzenie przeszłości. Istnieją pewne sformułowania problemów, w których rzadko lub niemożliwie dwie ścieżki osiągają ten sam stan. Przykładem może być problem z montażem, w którym każda akcja dodaje część do rozwijającego się złożenia i istnieje kolejność części tak, że można dodać, a potem, ale nie, a potem. W przypadku tych problemów możemy zaoszczędzić miejsce w pamięci, jeśli nie , nie śledź osiągniętych stanów i nie sprawdzamy nadmiarowych ścieżek. Algorytm wyszukiwania nazywamy przeszukiwaniem grafu, jeśli sprawdza on nadmiarowe ścieżki, a wyszukiwaniem podobnym do drzewa, jeśli nie sprawdza. Algorytm BEST-FIRST-SEARCH jest algorytmem przeszukiwania grafów; jeśli usuniemy wszystkie odniesienia, do których się udało, otrzymamy wyszukiwanie podobne do drzewa, które zużywa mniej pamięci, ale bada nadmiarowe ścieżki do tego samego stanu, a zatem będzie działać wolniej.

Po trzecie, możemy pójść na kompromis i sprawdzić cykle, ale ogólnie nie pod kątem nadmiarowych ścieżek. Ponieważ każdy węzeł ma łańcuch wskaźników nadrzędnych, możemy sprawdzić cykle bez potrzeby dodatkowej pamięci, podążając za łańcuchem rodziców, aby sprawdzić, czy stan na końcu ścieżki pojawił się wcześniej w ścieżce. Niektóre implementacje podążają za tym łańcuchem aż do góry, a tym samym eliminują wszystkie cykle; inne implementacje podążają tylko za kilkoma linkami (np. do rodzica, dziadka i pradziadka), a zatem zajmują tylko stałą ilość czasu, eliminując wszystkie krótkie cykle (i polegając na innych mechanizmach radzenia sobie z długimi cyklami).