Funkcje R mogą być stosowane rekurencyjnie. Funkcja rekurencyjna to funkcja, która wywołuje samą siebie, dopóki warunek nie zostanie spełniony. Używamy szeregu, który definiuje rozkład wykładniczy, aby zilustrować działanie funkcji rekurencyjnej.
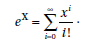
Potrzebujemy więc funkcji, która dodaje xi / i! na każdym kroku dla i równego 0, 1,…, n dla pewnego punktu zatrzymania . Ponieważ xi / i! zmniejsza się z każdym krokiem i staje się arbitralnie mały, użyliśmy rozmiaru xi / i! aby ustawić punkt zatrzymania.
Funkcja jest następująca:
> r.exp =
function (x, i = 0) {
if (abs (x ^ i / silnia (i))> 1,0e-8) {
r.exp (x, i + 1) + x ^ i / silnia (i)
}
else {
0
}
}
W pierwszym kroku rekurencji i jest równe zero, więc wartość r.exp() wynosi
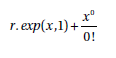
W drugim kroku wartość to
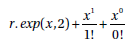
Jeśli i równe n jest ostatnim krokiem wcześniej xi / i! jest mniejsza niż nasz punkt zatrzymania 1,0e-8, to dla i równego n, wartość r.exp() jest równa
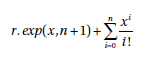
Ale
r.exp(x,n+1) = 0
więc rekurencja się zatrzymuje. Ponieważ wyrażenie w sekcji if funkcji jest ostatnią instrukcją wykonywaną w funkcji, funkcja zwraca wynik. Aby zobaczyć, jak działa funkcja, niech x będzie równe jeden:
> r.exp (1)
[1] 2,718282
> exp (1)
[1] 2,718282
Zauważ, że dla x równego jeden, funkcja daje taką samą wartość jak funkcja exp()