https://aie24.pl/
Wyobraź sobie prostego robota, R, w kształcie trójkąta prostokątnego, jak pokazano w lawendowym trójkącie w lewym dolnym rogu rysunku.
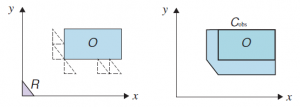
Robot musi zaplanować ścieżkę, która ominie prostokątną przeszkodę, O. Przestrzeń fizyczna, po której porusza się robot, nazywana jest przestrzenią roboczą. Ten konkretny robot może poruszać się w dowolnym kierunku w płaszczyźnie x-y, ale nie może się obracać. Rysunek przedstawia pięć innych możliwych pozycji robota z przerywanymi konturami; są one tak blisko przeszkody, jak robot może się dostać. Ciało robota może być przedstawione jako zbiór (x,y) punktów (lub (x,y, z) punktów dla robota trójwymiarowego), podobnie jak przeszkoda. Dzięki tej reprezentacji unikanie przeszkody oznacza, że żaden punkt na robocie nie zachodzi na żaden punkt na przeszkodzie. Planowanie ruchu wymagałoby obliczeń na zbiorach punktów, co może być skomplikowane i czasochłonne. Możemy uprościć obliczenia, używając schematu reprezentacji, w którym wszystkie punkty składające się na robota są reprezentowane jako pojedynczy punkt w abstrakcyjnej przestrzeni wielowymiarowej, którą nazywamy przestrzenią konfiguracji lub przestrzenią C. Chodzi o to, że zbiór punktów, które składają się na robota, można obliczyć, jeśli znamy (1) podstawowe wymiary robota (dla naszego trójkątnego robota wystarczy długość trzech boków) i (2) aktualna pozycja robota robota – jego pozycja i orientacja. W przypadku naszego prostego robota trójkątnego dla przestrzeni C wystarczą dwa wymiary: jeśli
znamy współrzędne (x,y) określonego punktu na robocie — użyjemy wierzchołka pod kątem prostym – wtedy możemy obliczyć, gdzie każdy inny punkt trójkąta to (ponieważ znamy rozmiar i kształt trójkąta i ponieważ trójkąt nie może się obracać). W lewym dolnym rogu rysunku trójkąt lawendowy może być reprezentowany przez konfigurację (0,0). Jeśli zmienimy reguły tak, aby robot mógł się obracać, będziemy potrzebować trzech wymiarów (x,y; ), aby móc obliczyć, gdzie znajduje się każdy punkt. Oto kąt obrotu robota w płaszczyźnie. Gdyby robot miał również zdolność do rozciągania się, wzrastając jednostajnie o współczynnik skalowania s, wówczas przestrzeń C miałaby cztery wymiary (x,y,θ s). Na razie pozostaniemy przy prostej dwuwymiarowej przestrzeni C robota z nieobrotowym trójkątem. Kolejnym zadaniem jest ustalenie, gdzie w przestrzeni C znajdują się punkty na przeszkodzie. Rozważ pięć trójkątów z linią przerywaną po lewej stronie rysunku 26.11 i zauważ, gdzie na każdym z nich znajduje się wierzchołek kąta prostego. Następnie wyobraź sobie wszystkie sposoby, w jakie trójkąt może się przesuwać. Oczywiście, wierzchołek pod kątem prostym nie może wejść do środka przeszkody, ani nie może zbliżyć się bliżej niż w żadnym z pięciu trójkątów z linią przerywaną. Widać więc, że obszar, do którego nie może dojść wierzchołek pod kątem prostym — przeszkoda w przestrzeni C – to pięcioboczny wielokąt po prawej stronie rysunku oznaczony Cobs W języku potocznym mówimy o wielu przeszkodach dla robot – stół, krzesło, jakieś ściany. Ale notacja matematyczna jest nieco łatwiejsza, jeśli pomyślimy o tym wszystkim jako o połączeniu w jedną „przeszkodę”, która ma rozłączone komponenty. Ogólnie rzecz biorąc, przeszkoda w przestrzeni C to zbiór wszystkich punktów q w C taki, że gdyby robot został umieszczony w tej konfiguracji, jego geometria przestrzeni roboczej przecinałaby przeszkodę w przestrzeni roboczej. Niech przeszkody w przestrzeni roboczej będą zbiorem punktów O, a zbiór wszystkich punktów na robocie w konfiguracji q będzie A(q). Wtedy przeszkoda w przestrzeni C jest zdefiniowana jako
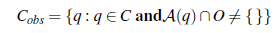
a wolna przestrzeń to Cfree =C-Cobs.
Przestrzeń C staje się bardziej interesująca dla robotów z ruchomymi częściami. Rozważ ramię z dwoma łącznikami z rysunku (a).
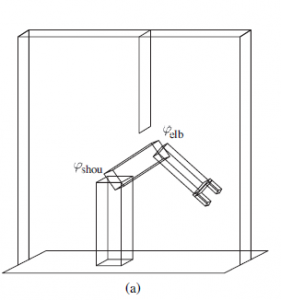
Jest przykręcony do stołu, więc podstawa się nie porusza, ale ramię ma dwa przeguby, które poruszają się w zależności od siebie – nazywamy te stopnie zaciśnięcia (DOF). Poruszanie stawami zmienia współrzędne (x,y) łokcia, chwytaka i każdego punktu na ramieniu. Przestrzeń konfiguracji ramienia jest dwuwymiarowa: ( θshou , θelb), gdzie θshou jest kątem stawu barkowego, a θelb jest kątem stawu łokciowego. Znajomość konfiguracji naszego ramienia z dwoma ogniwami oznacza, że możemy określić, gdzie znajduje się każdy punkt na ramieniu, za pomocą prostej trygonometrii. Ogólnie rzecz biorąc, mapowanie kinematyki do przodu jest funkcją
Φb : C->W
który przyjmuje konfigurację i wyświetla lokalizację określonego punktu b na robocie, gdy robot znajduje się w tej konfiguracji. Szczególnie przydatnym mapowaniem kinematyki do przodu jest mapowanie dla końcowego efektora robota, ΦEE. Zbiór wszystkich punktów na robocie w określonej konfiguracji q oznaczamy przez A(q) W:
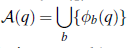
Odwrotny problem, polegający na mapowaniu pożądanej lokalizacji punktu na robocie do konfiguracji, w jakich musi się znajdować robot, aby to się stało, jest znany jako kinematyka odwrotna:
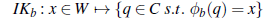
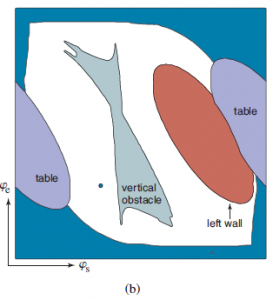
Czasami mapowanie kinematyki odwrotnej może przyjąć jako dane wejściowe nie tylko pozycję, ale także pożądaną orientację. Na przykład, gdy chcemy, aby manipulator chwycił obiekt, możemy obliczyć żądaną pozycję i orientację jego chwytaka oraz użyć kinematyki odwrotnej do określenia konfiguracji celu dla robota. Następnie planista musi znaleźć sposób na przeniesienie robota z jego obecnej konfiguracji do konfiguracji docelowej bez przecinania przeszkód. Przeszkody w przestrzeni roboczej są często przedstawiane jako proste formy geometryczne – zwłaszcza w podręcznikach robotyki, które skupiają się na przeszkodach wielokątnych. Ale jak wyglądają przeszkody w przestrzeni konfiguracyjnej? W przypadku ramienia z dwoma łącznikami proste przeszkody w przestrzeni roboczej, takie jak linia pionowa, mają bardzo złożone odpowiedniki w przestrzeni C, jak pokazano na rysunku 26.12(b). Różne odcienie zajmowanej przestrzeni odpowiadają różnym obiektom w przestrzeni roboczej robota: ciemny obszar otaczający całą wolną przestrzeń odpowiada konfiguracjom, w których robot zderza się ze sobą. Łatwo zauważyć, że ekstremalne wartości kątów barku czy łokcia powodują takie naruszenie. Dwa obszary o owalnym kształcie po obu stronach robota odpowiadają stolikowi, na którym robot jest zamontowany. Trzeci owalny obszar odpowiada lewej ścianie. Wreszcie najciekawszym obiektem w przestrzeni konfiguracyjnej jest pionowa przeszkoda, która zwisa z sufitu i utrudnia ruchy robota. Obiekt ten ma zabawny kształt w przestrzeni konfiguracji: jest wysoce nieliniowy, a miejscami wręcz wklęsły. Przy odrobinie wyobraźni czytelnik rozpozna kształt chwytaka na lewym górnym końcu. Zachęcamy czytelnika do chwili zatrzymania się i przestudiowania tego schematu. Kształt tej przeszkody w przestrzeni C wcale nie jest oczywisty! Kropka na rysunku (b) oznacza konfigurację robota na rysunku (a).
Rysunek przedstawia trzy dodatkowe konfiguracje, zarówno w przestrzeni roboczej, jak iw przestrzeni konfiguracyjnej.
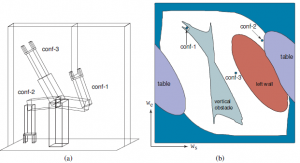
W konfiguracji konf-1 chwytak chwyta pionową przeszkodę. Widzimy, że nawet jeśli obszar roboczy robota jest reprezentowany przez płaskie wielokąty, kształt wolnej przestrzeni może być bardzo skomplikowany. W praktyce zatem zwykle sonduje się przestrzeń konfiguracyjną zamiast jawnie ją konstruować. Planista może wygenerować konfigurację, a następnie sprawdzić, czy znajduje się ona w wolnej przestrzeni, stosując kinematykę robota, a następnie sprawdzając kolizje we współrzędnych obszaru roboczego.



