Zamiast używać planera do tworzenia ścieżki kinematycznej i martwić się tylko dynamiką systemu po fakcie, tutaj omawiamy, w jaki sposób moglibyśmy zrobić to wszystko na raz. Weźmiemy problem optymalizacji trajektorii dla ścieżek kinematycznych i zamienimy go w prawdziwą optymalizację trajektorii z dynamiką: będziemy optymalizować bezpośrednio nad akcjami, biorąc pod uwagę dynamikę (lub przejścia). To znacznie przybliża nas do tego, co widzieliśmy w rozdziałach wyszukiwania i MDP. Jeśli znamy dynamikę systemu, możemy znaleźć sekwencję działań do wykonania, tak jak w rozdziale 3. Jeśli nie jesteśmy pewni, możemy potrzebować polityki, jak w rozdziale 16. W tej sekcji jesteśmy patrząc bardziej bezpośrednio na podstawowy MDP, w którym pracuje robot. Przechodzimy ze znanych dyskretnych MDP na ciągłe. Oznaczymy nasz dynamiczny stan świata przez x, jak jest to powszechna praktyka — odpowiednik s w dyskretnych MDP. Niech xs i xg będą stanami początkowym i docelowym. Chcemy znaleźć sekwencję akcji, które po wykonaniu przez robota dają pary stanów o niskim koszcie skumulowanym. Działaniami są momenty, które oznaczamy przez u(t) dla t zaczynając od 0 i kończąc na T. Formalnie chcemy znaleźć ciąg momentów u, które minimalizują skumulowany koszt J:
![]()
podlega ograniczeniom
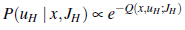
Jaki ma to związek z planowaniem ruchu i kontrolą śledzenia trajektorii? Cóż, wyobraźmy sobie, że usuwamy pojęcie sprawności i prześwitu z przeszkód i umieszczamy je w funkcji kosztu J, tak jak robiliśmy to wcześniej w optymalizacji trajektorii nad stanem kinematycznym. Stan dynamiczny to konfiguracja i prędkość, a momenty obrotowe u zmieniają je poprzez dynamikę f ze śledzenia trajektorii w otwartej pętli. Różnica polega na tym, że teraz myślimy jednocześnie o konfiguracjach i momentach obrotowych. Czasami możemy chcieć traktować unikanie kolizji również jako twarde ograniczenie, o czym wspomnieliśmy już wcześniej, przyglądając się optymalizacji trajektorii tylko dla stanu kinematycznego. Aby rozwiązać ten problem optymalizacji, możemy wziąć gradienty J — już nie w odniesieniu do sekwencji τ konfiguracji, ale bezpośrednio w odniesieniu do kontrolek u. Czasami pomocne jest uwzględnienie sekwencji stanów x również jako zmiennej decyzyjnej i użycie ograniczeń dynamiki, aby zapewnić, że x i u są spójne. Istnieją różne techniki optymalizacji trajektorii wykorzystujące to podejście; dwa z nich noszą nazwy wielokrotnego strzelania i bezpośredniej kolokacji. Żadna z tych technik nie znajdzie globalnego optymalnego rozwiązania, ale w praktyce mogą skutecznie sprawić, że roboty humanoidalne będą chodzić i prowadzić autonomiczne samochody. Magia ma miejsce, gdy w powyższym zadaniu J jest kwadratowe, a f jest liniowe względem x i u. Chcemy zminimalizować
![]()
Możemy optymalizować w nieskończonym horyzoncie, a nie skończonym, i uzyskujemy politykę z dowolnego stanu, a nie tylko z sekwencji kontroli. Aby to zadziałało, Q i R muszą być dodatnio określonymi macierzami. To daje nam liniowy regulator kwadratowy (LQR). W przypadku LQR optymalna funkcja wartości (zwana kosztem do przebycia) jest kwadratowa, a optymalna polityka jest liniowa. Polityka wygląda tak, jak u = -Kx, gdzie znalezienie macierzy K wymaga rozwiązania algebraicznego równania Riccati – nie jest potrzebna żadna lokalna optymalizacja, żadna iteracja wartości, żadna iteracja polityki nie jest potrzebna! Ze względu na łatwość znalezienia optymalnej polityki, LQR znajduje wiele zastosowań w praktyce, mimo że rzeczywiste problemy rzadko mają kwadratowe koszty i liniową dynamikę. Naprawdę użyteczną metodą jest metoda iteracyjna LQR (ILQR), która polega na rozpoczęciu od rozwiązania, a następnie iteracyjnym obliczeniu liniowej aproksymacji dynamiki i kwadratowej aproksymacji kosztów wokół niej, a następnie rozwiązaniu powstałego systemu LQR w celu uzyskania nowego rozwiązanie. Warianty LQR są również często używane do śledzenia trajektorii.