Omówiliśmy, jak planować ruchy, ale nie jak się poruszać — jak przykładać prąd do silników, wytwarzać moment obrotowy, poruszać robotem. To jest dziedzina teorii sterowania, dziedzina o coraz większym znaczeniu w sztucznej inteligencji. Należy sobie poradzić z dwoma głównymi pytaniami: w jaki sposób zamienić matematyczny opis ścieżki w sekwencję działań w świecie rzeczywistym (kontrola w otwartej pętli) oraz w jaki sposób upewniamy się, że pozostajemy na dobrej drodze (zamknięta pętla kontrola)? Od konfiguracji do momentów obrotowych do śledzenia w otwartej pętli: nasza ścieżka τ(t) daje nam konfiguracje. Robot zaczyna w spoczynku przy qs = τ(0). Stamtąd silniki robota zamieniają prądy w momenty obrotowe, prowadząc do ruchu. Ale do jakich momentów powinien dążyć robot, aby kończyć się na qg = τ(1)? W tym miejscu pojawia się idea modelu dynamicznego (lub modelu przejściowego). Możemy nadać robotowi funkcję f, która oblicza wpływ momentów obrotowych na konfigurację. Pamiętasz F = ma z fizyki? Cóż, jest coś takiego również dla momentów, w postaci 
gdzie u moment, 
prędkość, a 
Jeśli robot jest w konfiguracji q i prędkość oraz przyłożony moment obrotowy u, który doprowadziłby do przyspieszenia 
Krotka 
jest stanem dynamicznym, ponieważ zawiera prędkość, podczas gdy q jest stanem kinematycznym i nie jest wystarczająca do obliczenia dokładnego momentu, który należy zastosować. f jest deterministycznym modelem dynamiki w MDP w stanach dynamicznych z momentami obrotowymi jako działaniami. f-1 to dynamika odwrotna, która mówi nam, jaki moment zastosować, jeśli chcemy określonego przyspieszenia, które prowadzi do zmiany prędkości, a tym samym do zmiany stanu dynamicznego. Tera1z, naiwnie, moglibyśmy pomyśleć o t [0,1] jako o „czasie” w skali od 0 do 1 i wybrać nasz moment obrotowy za pomocą dynamiki odwrotnej:
zakładając, że robot zaczyna się o 
W rzeczywistości jednak sprawy nie są takie proste. Ścieżka została utworzona jako ciąg punktów, bez uwzględniania prędkości i przyspieszeń. Jako taka, ścieżka może nie spełniać wymagań ˙ τ(0) = 0 (robot startuje z prędkością 0), a nawet ,że τ jest różniczkowalna (nie mówiąc już o dwukrotnej różniczkowalności). Co więcej, znaczenie punktu końcowego „1” jest niejasne: ile sekund ma to odwzorowanie? W praktyce, zanim w ogóle pomyślimy o śledzeniu ścieżki odniesienia, zwykle zmieniamy jej czas, czyli przekształcamy w trajektorię ξ(t), która odwzorowuje przedział [0,T] przez pewien czas T na punkty w przestrzeni konfiguracyjnej C. (Symbol ξ to grecka litera Xi.) Powrót do tyłu jest trudniejszy, niż mogłoby się wydawać, ale istnieją przybliżone sposoby, aby to zrobić, na przykład wybierając maksymalną prędkość i przyspieszenie oraz używając profilu, który przyspiesza do tej maksymalnej prędkości , pozostaje tam tak długo, jak może, a następnie zwalnia z powrotem do 0. Zakładając, że możemy to zrobić, równanie (26.2) powyżej można przepisać jako
Nawet przy zmianie z rzeczywistej trajektorii τ na ξ , równanie przyłożenia momentów od góry (nazywane prawem sterowania) ma w praktyce problem. Wracając do sekcji uczenia się przez wzmacnianie, możesz zgadnąć, co to jest. Równanie działa świetnie w sytuacji, gdy f jest dokładne, ale nieznośna rzeczywistość staje się jak zwykle przeszkodą: w rzeczywistych układach nie możemy dokładnie zmierzyć mas i bezwładności, a f może nie uwzględniać prawidłowo zjawisk fizycznych, takich jak tarcie w silnikach (tarcie, które ma tendencję do uniemożliwiania wprawiania w ruch nieruchomych powierzchni – aby się przykleiły). Tak więc, gdy ramię robota zaczyna przykładać te momenty, ale f jest nieprawidłowe, błędy kumulują się i użytkownik coraz bardziej odchodzi od ścieżki odniesienia. Zamiast po prostu pozwalać na akumulację tych błędów, robot może użyć procesu sterowania, który sprawdza, gdzie według niego jest, porównuje to z tym, gdzie chciał się znajdować, i przykłada moment obrotowy, aby zminimalizować błąd. Regulator, który zapewnia siłę w ujemnej proporcji do zaobserwowanego błędu, nazywany jest regulatorem proporcjonalnym lub w skrócie regulatorem P. Równanie siły to:
gdzie qt jest bieżącą konfiguracją, a KP jest stałą reprezentującą współczynnik wzmocnienia regulatora. KP reguluje, jak mocno sterownik koryguje odchylenia między rzeczywistymi stanami qt i stan pożądany ξ(t).
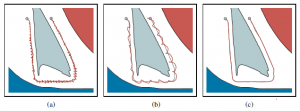
Za każdym razem, gdy wystąpi odchylenie — czy to z powodu hałasu, czy z powodu ograniczeń sił, które robot może zastosować — robot dostarcza przeciwną siłę, której wielkość jest proporcjonalna do tego odchylenia. Intuicyjnie może się to wydawać prawdopodobne, ponieważ odchylenia powinny być kompensowane przez siłę przeciwną, aby utrzymać robota na torze. Sterownik proporcjonalny może spowodować, że robot zastosuje zbyt dużą siłę, przekraczając pożądaną ścieżkę i poruszając się zygzakiem w przód iw tył. Wynika to z naturalnej bezwładności robota: po powrocie do pozycji odniesienia robot ma prędkość, której nie można natychmiast zatrzymać. Na rysunku 26.22(a) parametr KP = 1. Na pierwszy rzut oka można by pomyśleć, że wybranie mniejszej wartości KP rozwiąże problem, dając robotowi łagodniejsze podejście do pożądanej ścieżki. Niestety tak nie jest. Rysunek 26 (b) przedstawia trajektorię dla KP = .1, nadal wykazując zachowanie oscylacyjne. Niższa wartość parametru wzmocnienia pomaga, ale nie rozwiązuje problemu. W rzeczywistości, przy braku tarcia, regulator P jest zasadniczo prawem sprężyny; więc będzie oscylować w nieskończoność wokół ustalonej lokalizacji docelowej. Istnieje wiele sterowników, które są lepsze od prostego prawa proporcjonalnego sterowania. Mówi się, że sterownik jest stabilny, jeśli małe perturbacje prowadzą do ograniczonego błędu między robotem a sygnałem odniesienia. Mówi się, że jest całkowicie stabilny, jeśli jest w stanie powrócić, a następnie pozostać na swojej ścieżce odniesienia po takich perturbacjach. Nasz kontroler P wydaje się być stabilny, ale nie do końca stabilny, ponieważ nie znajduje się w pobliżu swojej trajektorii odniesienia. Najprostszym kontrolerem, który osiąga ścisłą stabilność w naszej domenie, jest kontroler PD. Litera „P” ponownie oznacza proporcjonalność, a „D” oznacza pochodną. Kontrolery PD są opisane następującym równaniem:
Jak sugeruje to równanie, regulatory PD rozszerzają regulatory P o składową różniczkową, która dodaje do wartości u(t) człon proporcjonalny do pierwszej pochodnej błędu ξ(t)-qt w czasie. Jaki jest skutek takiego terminu? Ogólnie rzecz biorąc, wyraz pochodny tłumi system, który jest kontrolowany. Aby to zobaczyć, rozważ sytuację, w której błąd zmienia się szybko w czasie, jak w przypadku naszego kontrolera P powyżej. Pochodna tego błędu będzie wówczas przeciwdziałać członowi proporcjonalnemu, co zmniejszy ogólną reakcję na zaburzenie. Jeśli jednak ten sam błąd utrzymuje się i nie zmienia się, pochodna zniknie, a człon proporcjonalny dominuje w wyborze kontroli. Rysunek (c) pokazuje wynik zastosowania tego kontrolera PD do ramienia naszego robota, używając jako parametrów wzmocnienia KP = .3 i KD = .8. Oczywiście uzyskana ścieżka jest znacznie gładsza i nie wykazuje żadnych widocznych oscylacji. Kontrolery PD mają jednak tryby awarii. W szczególności sterowniki PD mogą nie regulować błędu do zera, nawet przy braku zewnętrznych perturbacji. Często taka sytuacja jest wynikiem systematycznej siły zewnętrznej, która nie jest częścią modelu. Na przykład autonomiczny samochód jadący po nachylonej nawierzchni może być systematycznie ściągany na bok. Zużycie ramion robota powoduje podobne systematyczne błędy. W takich sytuacjach wymagana jest nieproporcjonalna informacja zwrotna, aby zbliżyć błąd do zera. Rozwiązanie tego problemu polega na dodaniu do prawa kontrolnego trzeciego członu, opartego na zintegrowanym błędzie w czasie:
Tutaj KI jest trzecim parametrem wzmocnienia. Składnik 
oblicza całkę błędu w czasie. Efektem tego składnika jest to, że długotrwałe odchylenia między sygnałem odniesienia a stanem rzeczywistym są korygowane. Składniki całkowe zapewniają zatem, że regulator nie wykazują systematyczny błąd długotrwały, chociaż stwarzają niebezpieczeństwo zachowania oscylacyjnego.Regulator ze wszystkimi trzema składnikami nazywany jest regulatorem PID (od proporcjonalnej pochodnej całkującej).Regulatory PID są szeroko stosowane w przemyśle, do różnych problemów ze sterowaniem. Pomyśl o trzech terminach w następujący sposób: proporcjonalny: spróbuj tym bardziej, im dalej jesteś od ścieżki; pochodna: spróbuj jeszcze bardziej, jeśli błąd rośnie; całka: spróbuj bardziej, jeśli nie robiłeś postępu przez długi czas. masa pomiędzy sterowaniem w pętli otwartej w oparciu o dynamikę odwrotną a sterowaniem PID w pętli zamkniętej nazywa się sterowaniem obliczonym momentem obrotowym. Obliczamy moment obrotowy, który według naszego modelu będzie potrzebny, ale kompensujemy niedokładność modelu za pomocą proporcjonalnych warunków błędu:
Pierwszy termin nosi nazwę komponentu sprzężenia do przodu, ponieważ wyszukuje kierunek, w którym robot musi się udać, i oblicza, jaki moment obrotowy może być wymagany. Drugi to składnik sprzężenia zwrotnego, ponieważ przekazuje bieżący błąd w stanie dynamicznym z powrotem do prawa sterowania m(q) jest macierzą bezwładności w konfiguracji q – w przeciwieństwie do normalnego sterowania PD, wzmocnienia zmieniają się wraz z konfiguracją systemu.