Algorytmy losowego próbkowania zwykle najpierw konstruują złożoną, ale wykonalną ścieżkę, a następnie ją optymalizują. Optymalizacja trajektorii działa odwrotnie: zaczyna się od prostej, ale niewykonalnej ścieżki, a następnie stara się wypchnąć ją z kolizji. Celem jest znalezienie ścieżki, która optymalizuje funkcję kosztu1 na ścieżkach. Oznacza to, że chcemy zminimalizować funkcję kosztu J(τ), gdzie τ(0) = qs i τ(1) = qg. J nazywa się funkcjonałem, ponieważ jest funkcją nad funkcjami. Argumentem J jest τ, który sam jest funkcją: τ(t) przyjmuje jako dane wejściowe punkt w przedziale [0,1] i odwzorowuje go na konfigurację. Funkcjonalność standardowego kosztu stanowi kompromis między dwoma ważnymi aspektami ruch robota: unikanie kolizji i wydajność, J = Jobs+ λJeff gdzie wydajność Jeff mierzy długość ścieżki i może również mierzyć gładkość. Wygodnym sposobem zdefiniowania wydajności jest metoda kwadratowa: całkuje pierwszą pochodną do kwadratu (za chwilę zobaczymy, dlaczego tak naprawdę zachęca to do krótkich ścieżek):
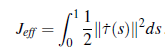
Jako składnik przeszkody załóżmy, że możemy obliczyć odległość d(x) od dowolnego punktu x W do najbliższej krawędzi przeszkody. Ta odległość jest dodatnia poza przeszkodami, 0 na krawędzi i ujemna . Nazywa się to polem odległości ze znakiem. Możemy teraz zdefiniować pole kosztu w obszar roboczy, nazwijmy go c, który ma wysoki koszt wewnątrz przeszkód i mały koszt na zewnątrz. Przy takim koszcie możemy sprawić, że punkty w przestrzeni roboczej naprawdę nienawidzą przebywania w przeszkodach i nie lubią być tuż obok nich (unikając problemu z wykresem widoczności polegającym na tym, że zawsze zwisają z krawędzi przeszkód). Oczywiście nasz robot nie jest punktem w przestrzeni roboczej, więc mamy jeszcze trochę pracy – musimy wziąć pod uwagę wszystkie punkty b na ciele robota:
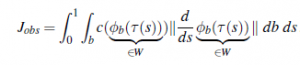
Nazywa się to całką po ścieżce — nie tylko całkuje c po drodze dla każdego punktu ciała, ale mnoży się przez pochodną, aby koszt był niezmienny w stosunku do zmiany czasu na ścieżce. Wyobraź sobie robota przeczesującego pole kosztów, akumulującego koszty, podobnie jak ruchy. Bez względu na to, jak szybko lub wolno ramię porusza się po polu, musi kumulować dokładnie taki sam koszt. Najprostszym sposobem rozwiązania powyższego problemu optymalizacji i znalezienia ścieżki jest opadanie gradientowe. Jeśli zastanawiasz się, jak obliczyć gradienty funkcjonałów względem funkcji, pomoże Ci coś, co nazywa się rachunkiem wariacyjnym. Jest to szczególnie łatwe dla funkcji formularza
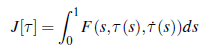
które są całkami funkcji, które zależą tylko od parametru s, wartości funkcji w s i pochodnej funkcji w s. W takim przypadku równanie Eulera-Lagrange’a mówi, że gradient wynosi

Jeśli przyjrzymy się uważnie Jeff i Jobs, obaj podążają za tym wzorem. W szczególności dla Jeff mamy F(s,τ(s),τ (s))= || (s)||2. Aby uzyskać nieco większy komfort, obliczmy gradient tylko dla Jeff. Widzimy, że F nie ma bezpośredniej zależności od τ(s), więc pierwszy wyraz we wzorze wynosi 0. Pozostaje nam
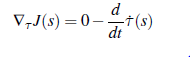
ponieważ pochodna cząstkowa F względem ˙ τs) wynosi ˙ τ(s). Zwróć uwagę, jak ułatwiliśmy sobie sprawę podczas definiowania Jeffa — jest to ładna kwadratowa pochodna (i nawet umieściliśmy 1/2 na początku, aby 2 ładnie się skreślało). W praktyce zobaczysz, że ta sztuczka zdarza się często w przypadku optymalizacji — sztuka polega nie tylko na wyborze sposobu optymalizacji funkcji kosztu, ale także na wybraniu funkcji kosztu, która będzie ładnie współpracować z tym, jak ją zoptymalizujesz. Upraszczając nasz gradient, otrzymujemy
![]()
Teraz, ponieważ Jeff jest kwadratem, ustawienie tego gradientu na 0 daje nam rozwiązanie τ, gdybyśmy nie mieli do czynienia z przeszkodami. Całkując raz, otrzymujemy, że pierwsza pochodna musi być stała; całkując ponownie otrzymujemy, że τ(s) = a ∙ s+b, gdzie a i b są określone przez ograniczenia punktu końcowego e dla τ(0) i τ(1). Optymalna ścieżka w stosunku do Jeff jest więc linią prostą od początku do celu! Jest to rzeczywiście najskuteczniejszy sposób przejścia od jednego do drugiego, jeśli nie ma przeszkód, o które trzeba się martwić. Oczywiście dodanie zadań jest tym, co utrudnia sprawę – i oszczędzimy ci tutaj wyprowadzania jego gradientu. Robot zazwyczaj inicjuje swoją ścieżkę jako linię prostą, która przebija się przez niektóre przeszkody. Następnie obliczyłaby gradient kosztu względem bieżącej ścieżki, a gradient służyłby odepchnięciu ścieżki od przeszkód . Należy pamiętać, że zjazd po pochyłościach znajdzie tylko lokalnie optymalne rozwiązanie – podobnie jak wspinaczka pod górę. Metody takie jak symulowane wyżarzanie mogą być użyte do poszukiwań, aby zwiększyć prawdopodobieństwo, że lokalne optimum jest dobre.