Percepcja to proces, w którym roboty mapują pomiary czujników na wewnętrzne reprezentacje środowiska. Wiele z nich wykorzystuje techniki widzenia komputerowego z poprzedniego rozdziału. Ale percepcja w robotyce musi zajmować się dodatkowymi czujnikami, takimi jak czujniki lidarowe i dotykowe. Percepcja jest trudna, ponieważ czujniki są hałaśliwe, a otoczenie częściowo obserwowalne, nieprzewidywalne i często dynamiczne. Innymi słowy, roboty mają wszystkie problemy z estymacją stanu (lub filtrowaniem), które omówiliśmy w rozdziale 14.2. Z reguły dobre reprezentacje wewnętrzne robotów mają trzy właściwości:
- Zawierają wystarczającą ilość informacji, aby robot mógł podejmować dobre decyzje.
- Są tak skonstruowane, aby można je było sprawnie aktualizować.
- Są naturalne w tym sensie, że zmienne wewnętrzne odpowiadają naturalnym zmiennym stanu w świecie fizycznym.
Wcześniej zobaczyliśmy, że filtry Kalmana, HMM i dynamiczne sieci Bayesa mogą reprezentować modele przejścia i czujniki częściowo obserwowalnego środowiska, i opisaliśmy zarówno dokładne, jak i przybliżone algorytmy aktualizacji stanu przekonania – rozkład prawdopodobieństwa a posteriori w środowisku. zmienne stanu. Przedstawiono kilka dynamicznych modeli sieci Bayesa dla tego procesu. W przypadku problemów z robotyką uwzględniamy w modelu własne przeszłe działania robota jako obserwowane zmienne.
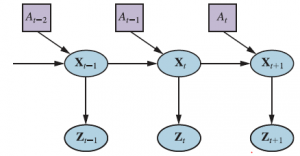
Rysunek pokazuje notację użytą w tym rozdziale: Xt to stan środowiska (w tym robota) w czasie t, Zt to obserwacja otrzymana w czasie t, a At to czynność podjęta po otrzymaniu obserwacji. Chcielibyśmy obliczyć nowy stan przekonań, P(Xt+1 | z1:t+1,a1:t), na podstawie obecnego stanu przekonań, P(Xt | z1:t ,a1:t-1) oraz nowa obserwacja zt+1. Są tu dwie różnice: warunkujemy zarówno działania, jak i obserwacje oraz mamy do czynienia ze zmiennymi ciągłymi, a nie dyskretnymi. W związku z tym modyfikujemy równanie filtrowania rekurencyjnego , aby używać całkowania zamiast sumowania:
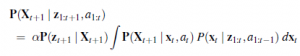
Równanie to stwierdza, że a posteriori zmiennych stanu X w czasie t+1 jest obliczana rekurencyjnie z odpowiedniego oszacowania o jeden krok wcześniej. Obliczenie to obejmuje poprzednią czynność przy i bieżący pomiar czujnika zt+1. Na przykład, jeśli naszym celem jest opracowanie robota do gry w piłkę nożną, Xt+1 może zawierać położenie piłki futbolowej względem robota. A posteriori P(Xt |z1:t , a1:t-1) to rozkład prawdopodobieństwa we wszystkich stanach, który wychwytuje to, co wiemy z poprzednich pomiarów i kontroli czujników. Równanie mówi nam, jak rekurencyjnie oszacować tę lokalizację, stopniowo składając pomiary czujników (np. obrazy z kamery) i polecenia ruchu robota. Prawdopodobieństwo P(Xt+1 | xt,at) nazywane jest modelem przejścia lub modelem ruchu, a P(zt+1 | Xt+1) jest modelem czujnika.