Co by było, gdyby docelowa RNN była warunkowana na wszystkich ukrytych wektorach ze źródłowej RNN, a nie tylko na ostatnim? Złagodziłoby to niedociągnięcia związane z sąsiednim odchyleniem kontekstu i ustalonymi limitami rozmiaru kontekstu, umożliwiając modelowi równie dobry dostęp do dowolnego poprzedniego słowa. Jednym ze sposobów uzyskania tego dostępu jest połączenie wszystkich ukrytych wektorów źródłowych RNN. Spowodowałoby to jednak ogromny wzrost liczby odważników, przy jednoczesnym wzroście czasu obliczeniowego, a także potencjalnie nadmierne dopasowanie. Zamiast tego możemy wykorzystać fakt, że gdy docelowy RNN generuje słowo docelowe jedno słowo na raz, jest prawdopodobne, że tylko niewielka część źródła jest rzeczywiście istotna dla każdego słowa docelowego. Co najważniejsze, docelowy RNN musi zwracać uwagę na różne części źródła dla każdego słowa. Załóżmy, że sieć jest przeszkolona do tłumaczenia angielskiego na hiszpański. Wyświetlane są słowa „Drzwi frontowe są czerwone”, po których następuje znacznik końca zdania, co oznacza, że nadszedł czas, aby rozpocząć pisanie hiszpańskich słów. Najlepiej więc najpierw zwrócić uwagę na „The” i wygenerować „La”, potem zwrócić uwagę na „drzwi” i wyjście „puerta” i tak dalej. Możemy sformalizować tę koncepcję za pomocą komponentu sieci neuronowej zwanego uwagą, który może być użyty do stworzenia „kontekstowego podsumowania” zdania źródłowego do reprezentacji o stałych wymiarach. Wektor kontekstowy ci zawiera najistotniejsze informacje do wygenerowania następnego słowa docelowego i będzie używany jako dodatkowe dane wejściowe do docelowego RNN. Model sekwencja-sekwencja, który wykorzystuje uwagę, nazywa się modelem uwagi sekwencja-sekwencja. Jeżeli standardowa docelowa RNN jest zapisana jako:
hi = RNN(hi-1,xi) ;
docelową RNN dla modeli uwagi sekwencja-sekwencja można zapisać jako:
hi = RNN(hi-1, [xi, ci])
gdzie [xi, ci] jest konkatenacją wektorów wejściowych i kontekstowych, ci, zdefiniowanych jako:
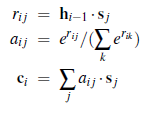
gdzie hi-1 jest docelowym wektorem RNN, który będzie używany do przewidywania słowa w kroku czasowym i, a s j jest wyjściem wektora źródłowego RNN dla słowa źródłowego (lub kroku czasowego) j. Zarówno hi-1, jak i sj są wektorami d-wymiarowymi, gdzie d jest ukrytym rozmiarem. Wartość rij jest zatem surowym „wynikiem uwagi” między bieżącym stanem docelowym a słowem źródłowym j. Te wyniki są następnie normalizowane do prawdopodobieństwa aij przy użyciu softmaxu dla wszystkich słów źródłowych. Wreszcie, prawdopodobieństwa te są wykorzystywane do generowania średniej ważonej źródłowych wektorów RNN, ci (inny wektor d-wymiarowy). Jest kilka ważnych szczegółów do zrozumienia. Po pierwsze, sam komponent uwagi nie ma wyuczonych wag i obsługuje sekwencje o zmiennej długości zarówno po stronie źródłowej, jak i docelowej. Po drugie, podobnie jak większość innych technik modelowania sieci neuronowych, o których się nauczyliśmy, uwaga jest całkowicie ukryta. Programista nie dyktuje, kiedy i jakie informacje zostaną użyte; model uczy się, czego używać. Uwaga ,można również połączyć z wielowarstwowymi sieciami RNN. W takim przypadku zazwyczaj zwraca się uwagę na każdą warstwę. Probabilistyczna formuła softmax dla uwagi służy trzem celom. Po pierwsze, umożliwia zróżnicowanie uwagi, co jest konieczne, aby można ją było wykorzystać z propagacją wsteczną. Mimo że sama uwaga nie ma wyuczonych wag, gradienty nadal płyną z powrotem przez uwagę do źródłowych i docelowych RNN. Po drugie, sformułowanie probabilistyczne umożliwia modelowi uchwycenie pewnych typów kontekstualizacji na duże odległości, które mogły nie zostać uchwycone przez źródłową RNN, ponieważ uwaga może rozważyć całą sekwencję źródłową na raz i nauczyć się zatrzymywać to, co jest ważne, i ignorować resztę . Po trzecie, uwaga probabilistyczna pozwala sieci reprezentować niepewność – jeśli sieć nie wie dokładnie, jakie słowo źródłowe ma przetłumaczyć w następnej kolejności, może rozłożyć prawdopodobieństwa uwagi na kilka opcji, a następnie faktycznie wybrać słowo, używając docelowego RNN. W przeciwieństwie do większości komponentów sieci neuronowych, prawdopodobieństwa uwagi są często interpretowane przez ludzi i intuicyjnie znaczące. Na przykład, w przypadku tłumaczenia maszynowego, prawdopodobieństwa uwagi często odpowiadają wyrównaniu między słowami, które wygenerowałby człowiek. Modele sekwencja-sekwencja są naturalne dla tłumaczenia maszynowego, ale prawie każde zadanie w języku naturalnym można zakodować jako problem sekwencja-sekwencja. Na przykład, system odpowiadania na pytania może być szkolony na danych wejściowych składających się z pytania, po którym następuje ogranicznik, po którym następuje odpowiedź.