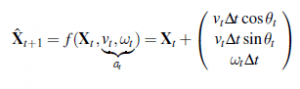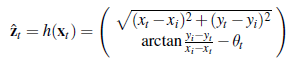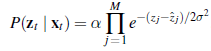https://aie24.pl/
Lokalizacja to problem z ustaleniem, gdzie znajdują się rzeczy — w tym sam robot. Aby lokalizacja była prosta, rozważmy robota mobilnego, który porusza się powoli w płaskim, dwuwymiarowym świecie. Załóżmy też, że robot otrzymuje dokładną mapę otoczenia. Pozę takiego robota mobilnego określają jego dwie współrzędne kartezjańskie o wartościach x i y oraz jego nagłówek o wartości θ , jak pokazano na rysunku (a).
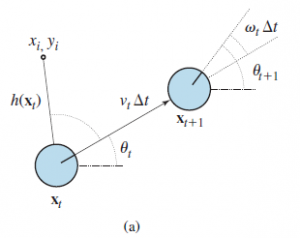
Jeśli ułożymy te trzy wartości w wektorze, to każdy konkretny stan jest określony przez Xt =(xt , yt , θt)T. Na razie w porządku. W przybliżeniu kinematycznym każde działanie składa się z „chwilowej” specyfikacji dwóch prędkości – prędkości translacyjnej vt i prędkości obrotowej ωt . Dla małych przedziałów czasu Δt, zgrubny deterministyczny model ruchu takich robotów jest podany przez
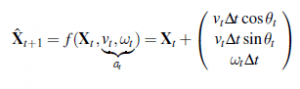
Notacja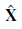 
odnosi się do deterministycznego przewidywania stanu. Oczywiście roboty fizyczne są nieco nieprzewidywalne. Jest to powszechnie modelowane przez rozkład Gaussa ze średnią f(Xt ,vt ,ωt) i kowariancją Σx
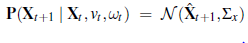
Ten rozkład prawdopodobieństwa to model ruchu robota. Modeluje wpływ ruchu na lokalizację at robota. Następnie potrzebujemy modelu czujnika. Rozważymy dwa rodzaje modeli czujników. Pierwsza zakłada, że czujniki wykrywają stabilne, rozpoznawalne cechy otoczenia zwane punktami orientacyjnymi. Dla każdego punktu orientacyjnego raportowany jest zasięg i namiar. Załóżmy, że stan robota to xt =(xt ,yt , θt)T i wykrywa on punkt orientacyjny, którego położenie jest znane jako (xi ,yi)T. Bez hałasu prognozę zasięgu i namiaru można obliczyć za pomocą prostej geometrii (patrz Rysunek (a)):
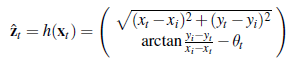
Znowu szum zniekształca nasze pomiary. Aby uprościć sprawę, załóżmy szum Gaussa z kowariancją Σz, dając nam model czujnika
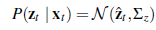
Nieco inny model czujnika jest używany do układu czujników zasięgu, z których każdy ma stałe łożysko względem robota. Takie czujniki wytwarzają wektor wartości zakresu
zt = (z1,…,zM)T.
Przy danej pozycji xt , niech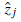 
będzie obliczonym zasięgiem wzdłuż j-tego kierunku wiązki od xt do najbliższej przeszkody. Tak jak poprzednio, zostanie to zepsute przez szum Gaussa. Zazwyczaj zakładamy, że błędy dla różnych kierunków wiązki są niezależne i identycznie rozłożone, więc mamy
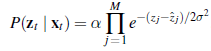
Rysunek (b) pokazuje przykład skanu czterowiązkowego i dwóch możliwych pozycji robota, z których jedna z dużym prawdopodobieństwem wygenerowała obserwowany skan, a druga nie.
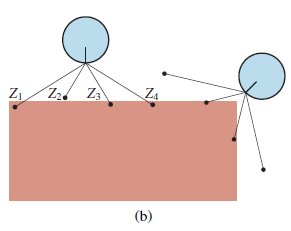
Porównując model ze skanowaniem odległości z modelem punktu orientacyjnego, widzimy, że model ze skanowaniem odległości ma tę zaletę, że nie ma potrzeby identyfikowania punktu orientacyjnego przed interpretacją skanowania odległości; w rzeczywistości na rysunku (b) robot stoi przed ścianą pozbawioną cech charakterystycznych. Z drugiej strony, jeśli istnieją widoczne, możliwe do zidentyfikowania punkty orientacyjne, mogą zapewnić natychmiastową lokalizację. Filtr Kalmana, reprezentuje stan przekonań jako pojedynczą wielowymiarową Gaussa, oraz filtr cząstek, który reprezentuje stan przekonań przez zbiór cząstek, które odpowiadają stanom. Większość współczesnych algorytmów lokalizacji wykorzystuje jedną z tych dwóch reprezentacji przekonań robota P(Xt | z1:t , a1:t-1). Lokalizacja za pomocą filtrowania cząstek nazywana jest lokalizacją Monte Carlo lub MCL. Rysunek przedstawia jedną wersję wykorzystującą model czujnika ze skanowaniem zakresu.
Działanie algorytmu ilustruje rysunek , gdy robot dowiaduje się, gdzie się znajduje w biurowcu.
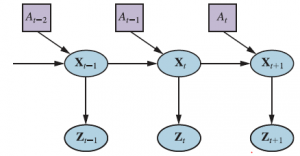
Na pierwszym zdjęciu cząstki są równomiernie rozłożone na podstawie wcześniejszego, co wskazuje na globalną niepewność co do pozycji robota. Na drugim obrazie pojawia się pierwszy zestaw pomiarów, a cząstki tworzą skupiska w obszarach wysokiego przekonania a posteriori. Po trzecie, dostępne są wystarczające pomiary, aby zepchnąć wszystkie cząstki w jedno miejsce. Filtr Kalmana to inny główny sposób lokalizacji. Filtr Kalmana reprezentuje tylne P(Xt | z1:t ,a1:t-1) przez Gaussa. Średnia tego Gaussa będzie oznaczona μt, a jej kowariancja Σt . Główny problem z wierzeniami Gaussa polega na tym, że są one zamknięte tylko dla modeli ruchu liniowego f i modeli pomiaru liniowego h. W przypadku nieliniowych f lub h wynik aktualizacji filtra na ogół nie jest gaussowski. W ten sposób algorytmy lokalizacji wykorzystujące filtr Kalmana linearyzują modele ruchu i czujników. Linearyzacja to lokalne przybliżenie funkcji nieliniowej przez funkcję liniową. Rysunek ilustruje koncepcję linearyzacji (jednowymiarowego) modelu ruchu robota.
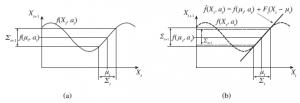
Po lewej stronie przedstawia nieliniowy model ruchu f(xt ,at) (kontrola at jest pominięta na tym wykresie, ponieważ nie odgrywa żadnej roli w linearyzacji). Po prawej stronie funkcja ta jest aproksymowana funkcją liniową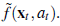 
Ta funkcja liniowa jest styczna do f w punkcie μt , czyli średniej naszego oszacowania stanu w czasie t. Taka linearyzacja nazywana jest rozwinięciem Taylora pierwszego stopnia. Filtr Kalmana, który linearyzuje f i h poprzez rozwinięcie Taylora, nazywany jest rozszerzonym filtrem Kalmana (lub EKF). Rysunek przedstawia sekwencję oszacowań robota obsługującego rozszerzony algorytm lokalizacji filtru Kalmana.
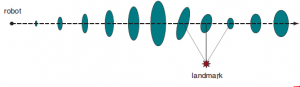
Gdy robot się porusza, niepewność oszacowania jego lokalizacji wzrasta, co pokazują wielokropki błędów. Jego błąd zmniejsza się, gdy wyczuwa zasięg i namiar na punkt orientacyjny o znanej lokalizacji, i ponownie wzrasta, gdy robot traci z oczu punkt orientacyjny. Algorytmy EKF działają dobrze, jeśli punkty orientacyjne są łatwo identyfikowane. W przeciwnym razie rozkład a posteriori może być multimodalny, jak na rycinie (b). Problem konieczności poznania tożsamości punktów orientacyjnych jest przykładem problemu asocjacji danych. W niektórych sytuacjach nie jest dostępna mapa otoczenia. Wtedy robot będzie musiał zdobyć mapę. To trochę problem z kurczakiem i jajkiem: nawigujący robot będzie musiał określić swoje położenie względem mapy, której nie do końca zna, jednocześnie budując tę mapę, nie znając do końca swojej rzeczywistej lokalizacji . Problem ten jest ważny dla wielu zastosowań robotów i był szeroko badany pod nazwą równoczesna lokalizacja i mapowanie, w skrócie SLAM. Problemy SLAM są rozwiązywane przy użyciu wielu różnych technik probabilistycznych, w tym rozszerzonego filtru Kalmana omówionego powyżej. Korzystanie z EKF jest proste: wystarczy rozszerzyć wektor stanu, aby uwzględnić lokalizacje punktów orientacyjnych w środowisku. Na szczęście aktualizacja EKF skaluje się kwadratowo, więc dla małych map (np. kilkuset punktów orientacyjnych) obliczenia są całkiem wykonalne. Bogatsze mapy są często otrzymywane przy użyciu metod relaksacji grafów, podobnych do technik wnioskowania sieci bayesowskich . Oczekiwanie – maksymalizacja jest również stosowana dla SLAM.
