Sieci resztkowe są popularnym i skutecznym podejściem do budowania bardzo głębokich sieci, które pozwalają uniknąć problemu znikających gradientów. Typowe modele głębokie wykorzystują warstwy, które uczą się nowej reprezentacji w warstwie i poprzez całkowite zastąpienie reprezentacji w warstwie i-1. Używając notacji macierzowo-wektorowej, którą wprowadziliśmy w równaniu , gdzie z(i) są wartościami jednostek w warstwie i, mamy
![]()
Ponieważ każda warstwa całkowicie zastępuje reprezentację z warstwy poprzedniej, wszystkie warstwy muszą nauczyć się robić coś pożytecznego. Każda warstwa musi przynajmniej zachowywać istotne dla zadania informacje zawarte w poprzedniej warstwie. Jeśli ustawimy W(i) = 0 dla dowolnej warstwy i, cała sieć przestanie działać. Gdybyśmy również ustawili W(i1) = 0, sieć nie byłaby nawet w stanie się uczyć: warstwa i nie uczyłaby się, ponieważ nie zaobserwowałaby żadnej zmiany danych wejściowych z warstwy i-1, a warstwa i-1 nie byłaby naucz się, ponieważ gradient wsteczny z warstwy i zawsze będzie wynosił zero. Oczywiście są to skrajne przykłady, ale ilustrują one potrzebę stosowania warstw jako kanałów dla sygnałów przechodzących przez sieć. Kluczową ideą sieci resztkowych jest to, że warstwa powinna zaburzać reprezentację z poprzedniej warstwy, a nie całkowicie ją zastępować. Jeśli wyuczona perturbacja jest niewielka, następna warstwa jest prawie kopią warstwy poprzedniej. Osiąga się to za pomocą następującego równania dla warstwy i jako warstwy i-1:
![]()
gdzie gr oznacza funkcje aktywacji dla warstwy resztkowej. Tutaj myślimy o f jako o reszcie, zaburzającej domyślne zachowanie przy przechodzeniu warstwy i1 do warstwy i. Funkcja używana do obliczenia reszty to zazwyczaj sieć neuronowa z jedną warstwą nieliniową połączoną z jedną warstwą liniową:
f(z) = Vg(Wz);
gdzie W i V to wyuczone macierze wag z dodanymi zwykłymi wagami odchylenia. Sieci resztkowe umożliwiają niezawodną naukę znacznie głębszych sieci. Zastanów się, co się stanie, jeśli ustawimy V=0 dla konkretnej warstwy, aby wyłączyć tę warstwę. Wtedy reszta f znika i Równanie upraszcza się do
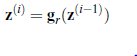
Załóżmy teraz, że gr składa się z funkcji aktywacji ReLU i że z(i-1) również stosuje funkcję ReLU do swoich wejść: z(i-1)=ReLU(in(i-1)). W takim razie mamy
![]()
gdzie następuje przedostatni krok, ponieważ ReLU(ReLU(x))=ReLU(x). Innymi słowy, w sieciach resztkowych z aktywacjami ReLU warstwa o zerowej wadze po prostu przekazuje swoje dane wejściowe bez zmiany. Reszta sieci działa tak, jakby warstwa nigdy nie istniała. Podczas gdy tradycyjne sieci muszą nauczyć się propagować informacje i są narażone na katastrofalne niepowodzenia w rozpowszechnianiu informacji z powodu złego doboru parametrów, pozostałe sieci domyślnie propagują informacje. Sieci resztkowe są często używane z warstwami splotowymi w aplikacjach wizyjnych, ale w rzeczywistości są narzędziem ogólnego przeznaczenia, które sprawia, że głębokie sieci są bardziej niezawodne i pozwalają naukowcom swobodniej eksperymentować ze złożonymi i heterogenicznymi projektami sieci. W chwili pisania tego tekstu nierzadko można zobaczyć szczątkowe sieci z setkami warstw. Projekt takich sieci szybko ewoluuje, więc wszelkie dodatkowe specyfikacje, które moglibyśmy podać, byłyby prawdopodobnie nieaktualne, zanim osiągnęłyby formę drukowaną. Czytelnicy pragnący poznać najlepsze architektury do konkretnych zastosowań powinni zapoznać się z najnowszymi publikacjami naukowymi.