Wyprowadziliśmy gradient funkcji straty względem wag w określonej (i bardzo prostej) sieci. Zaobserwowaliśmy, że gradient można obliczyć przez wsteczną propagację informacji o błędach z warstwy wyjściowej sieci do warstw ukrytych. Powiedzieliśmy również, że ten wynik generalnie obowiązuje dla każdego wykresu obliczeń z wyprzedzeniem. Tutaj wyjaśniamy, jak to działa. Rysunek przedstawia ogólny węzeł na wykresie obliczeń.
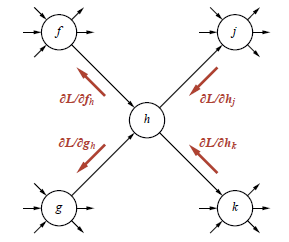
(Węzeł h ma stopień wejściowy i stopień zewnętrzny 2, ale nic w analizie od tego nie zależy.) Podczas przejścia do przodu węzeł oblicza pewną dowolną funkcję h ze swoich danych wejściowych, które pochodzą z węzłów f i g. Z kolei h przekazuje swoją wartość do węzłów j i k. Proces propagacji wstecznej przekazuje komunikaty z powrotem przez każde łącze w sieci. W każdym węźle zbierane są wiadomości przychodzące, a nowe wiadomości są obliczane, aby powrócić do następnej warstwy. Jak widać na rysunku, wszystkie komunikaty są częściowymi pochodnymi straty L. Na przykład komunikat wsteczny ∂/∂hj jest cząstkową pochodną L względem pierwszego wejścia j, które jest wiadomością przekazującą od h do j. Teraz h wpływa na L poprzez j i k, więc mamy
Za pomocą tego równania węzeł h może obliczyć pochodną L względem h przez zsumowanie wiadomości przychodzących od j i k. Teraz, aby obliczyć wychodzące wiadomości ∂L/∂fh i ∂L/∂gh, używamy następujących równań:
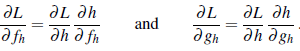
W równaniu drugim ∂L/∂h zostało już obliczone przez równanie pierwsze, a ∂h/∂fh i ∂h/∂gh są po prostu pochodnymi h odpowiednio względem pierwszego i drugiego argumentu. Na przykład, jeśli h jest węzłem mnożenia — to znaczy h(f,g) = f ∙ g – wtedy ∂h/∂fh/=g oraz ∂h/∂gh= f . Pakiety oprogramowania do uczenia głębokiego zazwyczaj zawierają bibliotekę typów węzłów (dodawanie, mnożenie, sigmoid itp.), z których każdy wie, jak obliczyć własne pochodne, zgodnie z wymaganiami równania . Proces propagacji wstecznej rozpoczyna się od węzłów wyjściowych, w których każdy komunikat początkowy 
jest obliczany bezpośrednio z wyrażenia na L pod względem przewidywanej wartości 
i prawdziwej wartości y z danych uczących. W każdym węźle wewnętrznym przychodzące wiadomości zwrotne są sumowane zgodnie z równaniem pierwszym, a wychodzące wiadomości są generowane z równania drugiego. Proces kończy się w każdym węźle na wykresie obliczeniowym, który reprezentuje wagę w . W tym momencie suma wiadomości przychodzących do w to ∂L/∂w – dokładnie gradient potrzebny do zaktualizowania w. Współdzielenie wag, stosowane w sieciach splotowych i sieciach rekurencyjnych , jest obsługiwane po prostu przez traktowanie każdej wspólnej wagi jako pojedynczego węzła z wieloma wychodzącymi łukami na grafie obliczeniowym. Podczas propagacji wstecznej powoduje to wiele przychodzących wiadomości gradientowych. Według równania pierwszego, oznacza to, że gradient dla wspólnej wagi jest sumą udziałów gradientu z każdego miejsca, w którym jest używany w sieci. Z tego opisu procesu propagacji wstecznej jasno wynika, że jego koszt obliczeniowy jest liniowy w stosunku do liczby węzłów w grafie obliczeniowym, podobnie jak koszt obliczeń w przód. Ponadto, ponieważ typy węzłów są zazwyczaj ustalone podczas projektowania sieci, wszystkie obliczenia gradientu można z wyprzedzeniem przygotować w formie symbolicznej i skompilować w bardzo wydajny kod dla każdego węzła na grafie. Należy również zauważyć, że komunikaty na rysunku nie muszą być skalarami: mogą to być w równym stopniu wektory, macierze lub tensory wyższych wymiarów, aby obliczenia gradientu można było mapować na GPU lub TPU, aby korzystać z paralelizmu. Jedną wadą propagacji wstecznej jest to, że wymaga przechowywania większości wartości pośrednich, które zostały obliczone podczas propagacji do przodu, w celu obliczenia gradientów w przejściu wstecznym. Oznacza to, że całkowity koszt pamięci uczenia sieci jest proporcjonalny do liczby jednostek w całej sieci. Tak więc, nawet jeśli reprezentowana jest sama sieć tylko niejawnie przez kod propagacji z wieloma pętlami, a nie jawnie przez strukturę danych, wszystkie pośrednie wyniki tego kodu propagacji muszą być przechowywane jawnie.