W próbie stworzenia agenta do gry w szachy wykazano przydatność określonego typu techniki RL, a mianowicie sieci SARSA. Sieć SARSA wraz z techniką wyszukiwania drzew Monte Carlo czyni cuda ze względu na jej zdolność do rozgrywania partii szachów poprzez planowanie z wyprzedzeniem, a nie tylko stosowanie polityki, która decyduje o wszystkim. Uzyskane wyniki są pozytywne, co wskazuje na sukces tej koncepcji.
Rysunek
przedstawia wyniki jednej sekwencji prób dla agenta ADP, która na każdym kroku jest zgodna z zaleceniem optymalnej polityki dla wyuczonego modelu. Agent nie uczy się prawdziwych narzędzi ani prawdziwej optymalnej polityki! Zamiast tego dzieje się tak, że w trzeciej próbie znajduje politykę, która osiąga nagrodę +1 na niższej trasie przez (2,1), (3,1), (3,2) i (3,3). (Patrz Rysunek (b). Po eksperymentowaniu z drobnymi zmianami, od ósmej próby dalej trzyma się tej polityki, nigdy nie ucząc się użyteczności innych stanów i nigdy nie znajdując optymalnej trasy przez (1, 2), (1, 3) i (2,3). Nazwiemy tego agenta zachłannym agentem, ponieważ na każdym kroku zachłannie podejmuje działania, które obecnie uważa za optymalne. Czasami chciwość się opłaca i agent dąży do optymalnej polityki, ale często tak się nie dzieje. Jak to możliwe, że wybór optymalnego działania prowadzi do nieoptymalnych wyników? Odpowiedź brzmi, że wyuczony model nie jest tym samym, co prawdziwe środowisko; co jest optymalne w nauczonym model może zatem być nieoptymalny w rzeczywistym środowisku. Niestety, agent nie wie, czym jest prawdziwe środowisko, więc nie może obliczyć optymalnego działania dla prawdziwego środowiska. Co więc powinien zrobić? Chciwy agent przeoczył fakt, że działania nie tylko zapewniają nagrody; dostarczają również informacji w postaci perceptów w powstałych stanach. Jak widzieliśmy w przypadku problemów z bandytami w sekcji 16.3, agent musi dokonać kompromisu między wykorzystaniem aktualnie najlepszej akcji, aby zmaksymalizować swoją krótkoterminową nagrodę, a eksploracją wcześniej nieznanych stanów w celu uzyskania informacji, które mogą prowadzić do zmiany polityki (i do większe nagrody w przyszłości). W prawdziwym świecie nieustannie trzeba wybierać między kontynuowaniem wygodnej egzystencji, a wyruszeniem w nieznane w nadziei na lepsze życie. Chociaż problemy z bandytami są trudne do rozwiązania dokładnie w celu uzyskania optymalnego schematu eksploracji, możliwe jest jednak wymyślenie schematu, który ostatecznie odkryje optymalną politykę, nawet jeśli może to potrwać dłużej niż jest to optymalne. Każdy taki schemat nie powinien być zachłanny w odniesieniu do najbliższego następnego ruchu, ale powinien być tak zwany „chciwy w granicy nieskończonej eksploracji” lub GLIE. Schemat GLIE musi wypróbować każdą akcję w każdym stanie nieograniczoną liczbę razy, aby uniknąć skończonego prawdopodobieństwa pominięcia optymalnej akcji. Agent ADP korzystający z takiego schematu w końcu nauczy się prawdziwego modelu przejścia, a następnie będzie mógł działać w warunkach eksploatacji. Istnieje kilka schematów GLIE; jednym z najprostszych jest nakłonienie agenta do wybrania losowej akcji w kroku czasowym t z prawdopodobieństwem 1=t, aw przeciwnym razie przestrzeganie polityki zachłanności. Chociaż ostatecznie zbiega się to do optymalnej polityki, może być powolne. Lepsze podejście nadałoby pewną wagę działaniom, których agent nie próbował zbyt często, jednocześnie unikając działań, które są uważane za mało użyteczne (tak jak zrobiliśmy to w przypadku przeszukiwania drzewa Monte Carlo). Można to zaimplementować zmieniając równanie ograniczające , tak aby przypisało wyższe oszacowanie użyteczności stosunkowo niezbadanym parom stan-działanie. To sprowadza się do optymistycznego wyprzedzenia możliwych środowisk i powoduje, że agent początkowo zachowuje się tak, jakby wszędzie były rozrzucone wspaniałe nagrody. Użyjmy U+(s) do oznaczenia optymistycznego oszacowania użyteczności (tj. oczekiwanej nagrody za przejście) stanu s i niech N(s;a) będzie liczbą prób działania a w stan s. Załóżmy, że używamy iteracji wartości w agencie uczącym ADP; następnie musimy przepisać równanie aktualizacji , aby uwzględnić optymistyczne oszacowanie:
Tutaj f jest funkcją eksploracji. Funkcja f (u,n) określa, w jaki sposób chciwość (preferencja wysokich wartości użyteczności u) jest wymieniana na ciekawość (preferowanie działań, które nie były często podejmowane i mają małą liczbę n). Funkcja powinna rosnąć w u i maleć w n. Oczywiście istnieje wiele możliwych funkcji, które pasują do tych warunków. Jedna szczególnie prosta definicja to:
gdzie R+ to optymistyczne oszacowanie najlepszej możliwej nagrody możliwej do uzyskania w dowolnym stanie, a Ne to stały parametr. Spowoduje to, że agent spróbuje każdej pary stan-działanie co najmniej Ne razy. Bardzo ważny jest fakt, że po prawej stronie równania pojawia się U+, a nie U. W miarę postępu eksploracji stany i działania w pobliżu stanu początkowego mogą być wypróbowywane wiele razy. Gdybyśmy użyli U, bardziej pesymistycznego oszacowania użyteczności, wówczas agent wkrótce byłby niechętny do eksploracji dalej. Użycie U+ oznacza, że korzyści z eksploracji są propagowane z obrzeży niezbadanych regionów, dzięki czemu działania prowadzące do niezbadanych regionów są ważone wyżej, a nie tylko działania, które same w sobie są nieznane. Skutki tej polityki poszukiwań widać wyraźnie na wykresie (b),
który pokazuje szybką konwergencję w kierunku zerowej utraty polityki, w przeciwieństwie do podejścia zachłannego. Bardzo prawie optymalną politykę można znaleźć już po 18 próbach. Zauważ, że błąd RMS w szacunkach użyteczności nie jest zbieżny tak szybko. Dzieje się tak, ponieważ agent dość szybko przestaje eksplorować niewdzięczne części przestrzeni stanu, a następnie odwiedza je tylko „przypadkowo”. Jednak ma sens, aby agent nie dbał o dokładną użyteczność stanów, o których wie, że są niepożądane i można ich uniknąć. Nie ma większego sensu poznawanie najlepszej stacji radiowej do słuchania spadając z klifu.
Wykres na rysunku pokazuje nagrodę, jaką każdy ruch wyprodukował podczas gry.
Wznoszący się wzór wskazuje, że agent nauczył się wykonywać znacznie lepsze ruchy, gdy gra więcej gier. Rysunek pokazuje, że w miarę postępów w rozgrywkach bilans materiałowy poprawiał się po każdej grze.
Oznacza to, że liczba bierek pozostałych po każdym meczu poprawia się. Oznacza to poprawę wydajności modelu. Rysunek przedstawia przykładowy interfejs użytkownika gry w szachy wraz z wynikami.
Agent biernego uczenia się ma ustaloną politykę, która określa jego zachowanie. Aktywny agent uczący się decyduje, jakie działania podjąć. Zacznijmy od agenta adaptacyjnego programowania dynamicznego (ADP) i zastanówmy się, jak można go zmodyfikować, aby wykorzystać tę nową wolność. Po pierwsze, agent będzie musiał nauczyć się pełnego modelu przejścia z prawdopodobieństwami wyniku dla wszystkich działań, a nie tylko modelu dla ustalonej polityki. Mechanizm uczenia się używany przez PASSIVE-ADP-AGENT wystarczy do tego. Następnie musimy wziąć pod uwagę fakt, że agent ma wybór działań. Narzędzia, których musi się nauczyć, to te określone przez optymalną politykę; przestrzegają równań Bellmana (które tutaj powtarzamy):
Równania te można rozwiązać w celu uzyskania funkcji użyteczności U przy użyciu algorytmów iteracji wartości lub iteracji polityki z rozdziału 16. Ostatnią kwestią jest to, co zrobić na każdym kroku. Po uzyskaniu funkcji użyteczności U, która jest optymalna dla wyuczonego modelu, agent może wyodrębnić optymalne działanie poprzez jednoetapowe wyprzedzenie, aby zmaksymalizować oczekiwaną użyteczność; alternatywnie, jeśli używa iteracji polityki, optymalna polityka jest już dostępna, więc może po prostu wykonać akcję zalecaną przez optymalną politykę. Ale czy powinno?
Keras: Aby załadować i zapisać model DNN zasad eksperckich.
Python-chess: Biblioteka symulacji szachów dla Pythona.
Składniki:
RLC_model.h5: Polityka ekspercka
Model Kerasa.
Agent: zawiera wszystkie wymagane funkcje, w tym strategię aktualizacji polityki.
Środowisko: zawiera funkcje związane z charakterystyką środowiska szachowego.
TD_search_m: zawiera kod symulacji gry i kod wyszukiwania MCTS.
Środowisko:
Cel: Efektywnie grać w szachy przeciwko ludzkiemu przeciwnikowi.
Środowisko jest budowane przy użyciu biblioteki o nazwie Python-chess. Rysunek pokazuje szachownicę stworzoną przez Python-chess.
Biblioteka zapewnia:
Fragment kodu : Pseudokod obliczający nagrodę za działanie w określonym stanie.
Obliczanie nagrody:
Strategie decyzyjne agenta – zasady:
Agent wykorzystuje dwa różne rodzaje strategii podejmowania decyzji, aby wykonać ruch. Oni są:
W każdym stanie agent poświęca 1 sekundę na rozszerzenie MCTS. Kroki wykonywane przez agenta przez 1 sekundę są pokazane na rysunku.
Są to:
Rozwiązanie podstawowego MDP, jak w poprzedniej sekcji, nie jest jedynym sposobem na zastosowanie równań Bellmana do problemu uczenia się. Innym sposobem jest wykorzystanie obserwowanych przejść do dostosowania użyteczności obserwowanych stanów tak, aby zgadzały się z równaniami więzów. Rozważmy na przykład przejście od (1,3) do (2,3) w drugiej próbie na stronie 843. Załóżmy, że w wyniku pierwszej próby oszacowania użyteczności wynoszą Uπ(1,3)=0,88 i Uπ (2;3)=0,:96. Teraz, gdyby to przejście od (1,3) do (2,3) zachodziło cały czas, oczekiwalibyśmy, że narzędzia będą zgodne z równaniem
Uπ(1,3) = -0:04+Uπ(2,3) ;
więc Uπ(1,3) byłoby 0,92. Tym samym jego obecne szacunki na poziomie 0,88 mogą być nieco zaniżone i powinny zostać podwyższone. Mówiąc bardziej ogólnie, gdy następuje przejście ze stanu s do stanu s’ poprzez akcję (s), stosujemy następującą aktualizację do π(s):
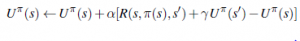
Tu α to parametr szybkości uczenia się. Ponieważ ta reguła aktualizacji wykorzystuje różnicę użyteczności między kolejnymi stanami (a tym samym kolejnymi czasami), jest często nazywana równaniem różnicy czasowej (TD). Podobnie jak w zasadach aktualizacji wag , termin TD R(s,π (s); s’)+ γUπ(s’)-Uπ(s) jest efektywnie sygnał błędu, a aktualizacja ma na celu zmniejszenie błędu. Wszystkie metody różnic czasowych działają poprzez dostosowanie oszacowań użyteczności w kierunku idealnej równowagi, która utrzymuje się lokalnie, gdy oszacowania użyteczności są prawidłowe. W przypadku uczenia się pasywnego równowaga jest dana równaniem
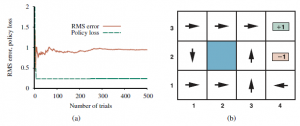
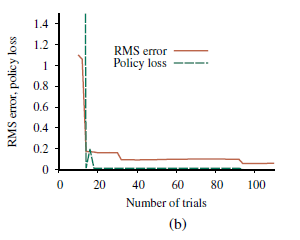
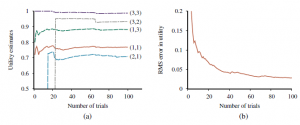
Tu α to parametr szybkości uczenia się. Ponieważ ta reguła aktualizacji wykorzystuje różnicę użyteczności między kolejnymi stanami (a tym samym kolejnymi czasami), jest często nazywana równaniem różnicy czasowej (TD). Podobnie jak w zasadach aktualizacji wag , termin TD R(s,π (s); s’)+ γUπ(s’)-Uπ(s) jest efektywnie sygnał błędu, a aktualizacja ma na celu zmniejszenie błędu. Wszystkie metody różnic czasowych działają poprzez dostosowanie oszacowań użyteczności w kierunku idealnej równowagi, która utrzymuje się lokalnie, gdy oszacowania użyteczności są prawidłowe. W przypadku uczenia się pasywnego równowaga jest dana równaniem). Teraz powyższe faktycznie powoduje, że agent osiąga równowagę podaną przez równanie wcześniejsze, ale wiąże się to z pewną subtelnością. Po pierwsze, zauważ, że aktualizacja dotyczy tylko obserwowanego następcy s0, podczas gdy rzeczywiste warunki równowagi obejmują wszystkie możliwe kolejne stany. Można by pomyśleć, że powoduje to niewłaściwie dużą zmianę Uπ(s), gdy występuje bardzo rzadkie przejście; ale w rzeczywistości, ponieważ rzadkie przejścia występują rzadko, średnia wartość Uπ(s) zbiegnie się do prawidłowej wartości w limicie, nawet jeśli sama wartość będzie się zmieniać. Co więcej, jeśli zmienimy parametr w funkcję, która zmniejsza się wraz ze wzrostem liczby odwiedzin danego stanu, wówczas samo Uπ(s) zbiegnie się do prawidłowej wartości. Rysunek ilustruje wydajność pasywnego agenta TD na świecie 4 3.
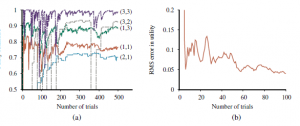
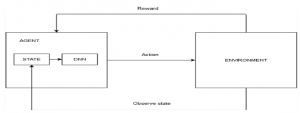
Nie uczy się tak szybko jak agent ADP i wykazuje znacznie większą zmienność, ale jest znacznie prostszy i wymaga znacznie mniej obliczeń na obserwację. Zauważyłem, że TD nie potrzebuje modelu przejściowego do przeprowadzenia aktualizacji. Samo środowisko zasila połączenia między sąsiadującymi państwami w postaci obserwowanych przejść. Podejścia ADP i TD są ze sobą ściśle powiązane. Obaj starają się dokonywać lokalnych korekt szacunków użyteczności, aby każdy stan „zgadzał się” ze swoimi następcami. Jedną z różnic jest to, że TD dostosowuje stan, aby zgadzał się z obserwowanym następcą (Równanie (23.3)), podczas gdy ADP dostosowuje stan, aby zgadzał się ze wszystkimi następcami, które mogą wystąpić, ważonymi ich prawdopodobieństwami . Ta różnica znika, gdy efekty korekt TD są uśredniane dla dużej liczby przejść, ponieważ częstotliwość każdego następcy w zestawie przejść jest w przybliżeniu proporcjonalna do jego prawdopodobieństwa. Ważniejsza różnica polega na tym, że podczas gdy TD dokonuje pojedynczej korekty na obserwowane przejście, ADP dokonuje tyle, ile potrzeba, aby przywrócić spójność między oszacowaniami użyteczności U a modelem przejścia P. Chociaż obserwowane przejście powoduje tylko lokalną zmianę w P, jego efekty mogą wymagać propagowania w całym U. Tak więc TD można postrzegać jako prymitywne, ale skuteczne pierwsze przybliżenie do ADP. Każda korekta dokonana przez ADP mogła być postrzegana, z punktu widzenia TD, jako wynik pseudodoświadczenia wygenerowanego przez symulację obecnego modelu przejścia. Możliwe jest rozszerzenie podejścia TD o wykorzystanie modelu przejścia do generowania kilku pseudodoświadczeń – przejść, które agent TD może sobie wyobrazić, biorąc pod uwagę jego obecny model. Dla każdego obserwowanego przejścia agent TD może wygenerować dużą liczbę urojonych przejść. W ten sposób uzyskane szacunki użyteczności będą coraz bardziej zbliżać się do tych z ADP – oczywiście kosztem wydłużenia czasu obliczeń. W podobnym duchu możemy generować wydajniejsze wersje ADP, bezpośrednio przybliżając algorytmy iteracji wartości lub iteracji polityki. Chociaż algorytm iteracji wartości jest wydajny, jest niewykonalny, jeśli mamy, powiedzmy, 10100 stanów. Jednak wiele niezbędnych korekt wartości stanu w każdej iteracji będzie bardzo małych. Jednym z możliwych podejść do szybkiego generowania dość dobrych odpowiedzi jest ograniczenie liczby korekt dokonywanych po każdym zaobserwowanym przejściu. Można również użyć heurystyki, aby uszeregować możliwe korekty tak, aby przeprowadzić tylko te najważniejsze. Szeroko zakrojona heurystyka z priorytetami woli dokonywać korekt stanów, których prawdopodobni następcy właśnie przeszli dużą korektę w swoich własnych szacunkach użyteczności.
Używając takiej heurystyki, przybliżone algorytmy ADP mogą uczyć się mniej więcej tak szybko, jak pełne ADP, pod względem liczby sekwencji treningowych, ale mogą być o rząd wielkości bardziej wydajne pod względem obliczeń całkowitych. Dzięki temu mogą obsługiwać przestrzenie stanów, które są zbyt duże dla pełnego ADP. Przybliżone algorytmy ADP mają dodatkową zaletę: na wczesnych etapach uczenia się nowego środowiska model przejścia P często będzie daleki od poprawności, więc nie ma sensu obliczać dokładnej funkcji użyteczności, która by mu odpowiadała. Algorytm aproksymacyjny może używać minimalnego rozmiaru korekty, który zmniejsza się, gdy model przejścia staje się dokładniejszy. Eliminuje to bardzo długie cykle iteracji wartości, które mogą wystąpić na wczesnym etapie uczenia się z powodu dużych zmian w modelu.
Stany: zbiór wszystkich stanów; tutaj jest to zestaw wszystkich pozycji figur szachowych na szachownicy.
Polityka: Jest to tabela stan-działanie z wartościami odpowiadającymi każdej parze.
Funkcja wartości: Funkcja wartości zastosowana w tym badaniu to tradycyjne równanie Bellmana.
Gdzie Q(St,At) – prawdopodobieństwo wygranej ze stanu St poprzez wykonanie akcji At, Rt – Nagroda przy St, α – szybkość uczenia się, a γ – współczynnik dyskontowy (znaczenie przyszłej nagrody)
Akcje: Zawiera wszystkie możliwe ruchy, które dana figura może wykonać z pozycji, biorąc pod uwagę wszystkie ograniczenia środowiskowe.
Agent: Agent jest organem decyzyjnym naszego systemu. Reprezentuje bota AI, który gra w szachy. Posiada zdolność postrzegania otoczenia i podejmowania działań wpływających na otoczenie
Otoczenie: Oto środowisko to szachownica. Zawiera wszystkie pionki wraz z zasadami rządzącymi ich ruchem. Zawiera ideę nagród, wartość każdego elementu. Odpowiada agentowi, zwracając agentowi nagrodę za każde jego działanie.
MCTS: Ta technika jest używana przez agenta, aby wyczekiwać gry poprzez zastosowanie symulacji pionów. Oczekiwanie odbywa się za pomocą tego MCTS. To drzewo zawiera:
Węzły: stan szachownicy.
Krawędzie: Akcje i odpowiadające im wartości łączące stan S z S’.
To drzewo jest budowane, gdy agent gra przeciwko ludzkiemu przeciwnikowi. Drzewo jest początkowo inicjowane z wartościami losowymi, ale w miarę rozgrywania większej liczby gier drzewo jest aktualizowane o ruchy wraz z wynikiem zaufania. To właśnie ten wynik ufności jest później wykorzystywany do ponownego zastosowania symulacji.
Polityka ekspercka: W MCTS, aby wykonać te symulacje, musi istnieć polityka, która jest używana do wybierania kolejnych stanów potomnych wymaganych do symulacji. Stosowana tutaj polityka ekspercka to gęsto warstwowa sieć neuronowa. Ten DNN jest trenowany jednocześnie z agentem, gdy agent gra w szachy. Stany przechowywane w MCTS są wykorzystywane jako trening dla tego modelu.
Pracujący:
Agent adaptacyjnego programowania dynamicznego (lub ADP) wykorzystuje ograniczenia między użytecznościami stanów, ucząc się modelu przejścia, który je łączy i rozwiązując odpowiedni proces decyzyjny Markowa za pomocą programowania dynamicznego. W przypadku pasywnego agenta uczącego oznacza to podłączenie wyuczonego modelu przejścia P(s’ | s; π(s)) i obserwowanych nagród R(s, π(s), s’) do równania w celu obliczenia użyteczności stanów . Jak zauważyliśmy w naszej dyskusji na temat iteracji polityki , te równania Bellmana są liniowe, gdy polityka π jest ustalona, więc można je rozwiązać przy użyciu dowolnego pakietu algebry liniowej. Alternatywnie, możemy przyjąć podejście iteracji zmodyfikowanej polityki , używając uproszczonego procesu iteracji wartości w celu aktualizacji oszacowań użyteczności po każdej zmianie wyuczonego modelu. Ponieważ model zwykle zmienia się tylko nieznacznie z każdą obserwacją, proces iteracji wartości może wykorzystywać poprzednie oszacowania użyteczności jako wartości początkowe i zazwyczaj bardzo szybko się zbiegają. Nauka modelu przejścia jest łatwa, ponieważ środowisko jest w pełni obserwowalne. Oznacza to, że mamy nadzorowane zadanie uczenia się, w którym danymi wejściowymi dla każdego przykładu uczącego jest para stan-działanie (s,a), a wyjściem jest stan wynikowy s’. Model przejścia P(s’ |s,a) jest reprezentowany w postaci tabeli i jest szacowany bezpośrednio na podstawie zliczeń zgromadzonych w Ns’0|sa. Liczby rejestrują, jak często stan s’ jest osiągany podczas wykonywania a w s. Na przykład, w trzech próbach ,Prawo jest wykonywane cztery razy w (3,3), a wynikowy stan to (3,2) dwa razy i (4,3) dwa razy, więc P((3,2) j (3,3),Prawo) i P((4,3) j (3,3),Prawo) szacuje się na 12 . Pełny program agenta dla pasywnego agenta ADP pokazano tu
Jego wydajność na świecie 4 3 pokazano na rysunku .
Jeśli chodzi o szybkość poprawy oszacowań wartości, agent ADP jest ograniczony jedynie zdolnością uczenia się modelu przejścia. W tym sensie zapewnia standard, w stosunku do którego można mierzyć inne algorytmy uczenia się przez wzmacnianie. Jest jednak niewykonalny w przypadku dużych przestrzeni państwowych. Na przykład w tryktraku wymagałoby to rozwiązania około 1020 równań w 1020 niewiadomych.
Systemem wybranym do tworzenia i testowania agenta szachowego jest sieć SARSA [7], która realizuje koncepcję przeszukiwania drzewa Monte Carlo (MCTS). W tym przypadku sieć SARSA wdraża koncepcje uczenia się przez wzmacnianie jako technikę on-policy. Technika on-policy odnosi się do modelu RL, który uczy się swojej polityki, gdy wchodzi w interakcję ze środowiskiem, więc interakcja i uczenie się agenta z otoczeniem zachodzą jednocześnie. Architekturę proponowanego agenta szachowego przedstawiono na rysunku .
Ideą bezpośredniego szacowania użyteczności jest to, że użyteczność stanu jest definiowana jako oczekiwana całkowita nagroda od tego stanu (nazywana oczekiwaną nagrodą-to-go) i że każda próba dostarcza próbki tej wielkości dla każdego odwiedzonego stanu. Na przykład pierwsza z trzech prób pokazane wcześniej zapewniają całkowitą nagrodę próbki 0,76 dla stanu (1,1), dwie próbki 0,80 i 0,88 dla (1,2), dwie próbki 0,84 i 0,92 dla (1,3) i tak dalej. Tak więc na końcu każdej sekwencji algorytm oblicza obserwowaną nagrodę do przejścia dla każdego stanu i odpowiednio aktualizuje szacowaną użyteczność dla tego stanu, po prostu utrzymując średnią bieżącą dla każdego stanu w tabeli. W limicie nieskończenie wielu prób średnia z próbki zbiegnie się z prawdziwym oczekiwaniem w równaniu (23.1). Oznacza to, że ograniczyliśmy uczenie się przez wzmacnianie do standardowego nadzorowanego problemu uczenia się, w którym każdy przykład jest parą (stan, nagroda-to-go). Mamy wiele potężnych algorytmów do nadzorowanego uczenia się, więc to podejście wydaje się obiecujące, ale ignoruje ważne ograniczenie: użyteczność stanu jest określana przez nagrodę i oczekiwaną użyteczność J stanów następczych. Dokładniej, wartości użyteczności są zgodne z równaniami Bellmana dla ustalonej polisy:
Ignorując powiązania między stanami, bezpośrednie szacowanie użyteczności pomija możliwości uczenia się. Na przykład druga z trzech podanych wcześniej prób osiąga stan (3,2), który nie był wcześniej odwiedzany. Kolejne przejście osiąga wartość (3,3), o której wiadomo z pierwszej próby, że ma wysoką użyteczność. Równanie Bellmana od razu sugeruje, że (3,2) prawdopodobnie ma również wysoką użyteczność, ponieważ prowadzi do (3,3), ale bezpośrednie oszacowanie użyteczności niczego się nie uczy do końca próby. Mówiąc szerzej, bezpośrednią estymację użyteczności możemy postrzegać jako poszukiwanie U w przestrzeni hipotez, która jest znacznie większa niż to konieczne, ponieważ zawiera wiele funkcji, które naruszają równania Bellmana. Z tego powodu algorytm często zbiega się bardzo powoli.