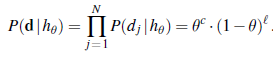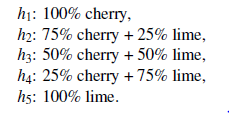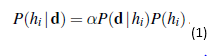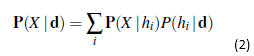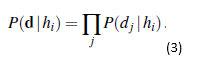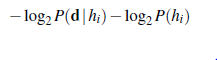Miesiąc: listopad 2022

https://aie24.pl/

Ta sekcja podkreśla ograniczenia obecnych praktyk klinicznych. Ponadto omówiono nowe ramy zaproponowane przez amerykański Narodowy Instytut Zdrowia Psychicznego (NIMH) dla oceny i leczenia znanych jako perspektywy biopsychospołeczne zaburzeń psychicznych. Zdrowie psychiczne to nie tylko brak dysfunkcyjnych myśli, zachowań i emocji, które powodują znaczny stres lub upośledzenie, ale także obecność subiektywnego dobrostanu . W raporcie Światowej Organizacji Zdrowia (WHO) z 2001 r. stwierdzono, że na początku XXI wieku na zaburzenia psychiczne cierpiało około 450 milionów ludzi, wskazując zaburzenia psychiczne jako jedną z głównych przyczyn złego stanu zdrowia i niepełnosprawności na całym świecie. Raport NIMH z 2011 r. poinformował, że zaburzenia psychiczne stanowią 13% globalnego obciążenia chorobami, przewyższając choroby układu krążenia i nowotwory . W raporcie wymieniono depresję jako trzeci główny czynnik przyczyniający się do globalnego obciążenia chorobami. Raport przewidywał, że do 2020 roku 1,5 miliona ludzi może umrzeć przez samobójstwo każdego roku, a 15–30 milionów osób podejmie próbę samobójstwa. Konceptualizacja zaburzeń psychicznych jako anormalnych doświadczeń psychologicznych i traktowanie tych doświadczeń jako chorób przeszła 200-letnią podróż, kiedy interpretowaliśmy choroby psychiczne jako karę Bożą lub wynik sił religijnych lub nadprzyrodzonych. Warto przyznać, że praktyki w zakresie zdrowia psychicznego przeszły długą drogę, zyskując dziś powszechną uwagę i stając się częścią podstawowej opieki zdrowotnej i badań. Tradycyjne obserwacje kliniczne z udziałem klinicystów i subiektywne raporty pacjentów na temat objawów zachowania, myśli i emocji były szeroko krytykowane za ujęcie codziennych, bogatych, złożonych ustawień funkcjonalnych w ramach oceny klinicznej opartej na Diagnostycznym i Statystycznym Podręczniku Zaburzeń Psychicznych (DSM) . Chociaż DSM dostarcza użytecznych ram do klasyfikacji zaburzeń psychicznych, nie jest w stanie odwzorować najnowszych odkryć naukowych dotyczących chorób psychicznych z perspektywy biopsychospołecznej . W poglądach biopsychospołecznych czynniki biologiczne koncentrują się na genetyce i epigenetyce, zaburzeniach równowagi biochemicznej i mózgowych korelatach nieprawidłowości; czynniki psychologiczne skupiają się na nieadaptacyjnych mechanizmach uczenia się i radzenia sobie, uprzedzeniach poznawczych, dysfunkcjonalnej postawie i problemach interpersonalnych; a czynniki społeczne koncentrują się na słabej socjalizacji, stresujących doświadczeniach życiowych, kulturze i nierównościach społecznych . Zdając sobie sprawę ze znaczenia czynników psychospołeczno-biologicznych, NIMH zaproponował nowe ramy badań nad zdrowiem psychicznym i dobrostanem. Zaleciła przeniesienie uwagi z kategorii DSM na bardziej biologiczne, psychologiczne/poznawcze i behawioralne konstrukty jako elementy budulcowe zaburzeń psychicznych .

https://aie24.pl/

Prawdopodobnie najpopularniejszym modelem sieci bayesowskim używanym w uczeniu maszynowym jest naiwny model Bayesa. W tym modelu zmienna „klasy” C (która należy przewidzieć) jest pierwiastkiem, a zmienne „atrybutu” X_i są liście. Model jest „naiwny”, ponieważ zakłada, że atrybuty są od siebie warunkowo niezależne, biorąc pod uwagę klasę. Model na rysunku 21.2(b) jest naiwnym modelem Bayesa z klasą Flavor i tylko jednym atrybutem Wrapper). W przypadku zmiennych logicznych parametry są

Po przeszkoleniu modelu w ten sposób można go użyć do klasyfikowania nowych przykładów, dla których zmienna klasy C nie jest obserwowana. Z zaobserwowanymi wartościami atrybutów x₁,…,x_n, prawdopodobieństwo każdej klasy jest podane przez

Predykcję deterministyczną można uzyskać, wybierając najbardziej prawdopodobną klasę. Rysunek  pokazuje krzywą uczenia się dla tej metody, gdy jest ona zastosowana do problemu restauracji  

Metoda uczy się dość dobrze, ale nie tak dobrze, jak uczenie się drzewa decyzyjnego; przypuszczalnie dzieje się tak dlatego, że prawdziwa hipoteza – która jest drzewem decyzyjnym – nie jest dokładnie odwzorowana przy użyciu naiwnego modelu Bayesa. Uczenie się naiwnego Bayesa okazuje się zaskakująco dobre w szerokim zakresie zastosowań; wersja wzmocniona jest jednym z najskuteczniejszych algorytmów uczenia ogólnego przeznaczenia. Naiwne uczenie Bayesa skaluje się dobrze do bardzo dużych problemów: przy n atrybutach logicznych istnieje tylko 2n+1 parametrów i nie jest wymagane wyszukiwanie, aby znaleźć h_ML, naiwną hipotezę Bayesa o maksymalnym prawdopodobieństwie. Wreszcie, naiwne systemy uczenia Bayesa dobrze radzą sobie z zaszumionymi lub brakującymi danymi iw razie potrzeby mogą dawać probabilistyczne przewidywania. Ich podstawową wadą jest fakt, że założenie warunkowej niezależności rzadko jest trafne;  założenie to prowadzi do zbyt pewnych prawdopodobieństw, które często są bardzo bliskie 0 lub 1, szczególnie przy dużej liczbie atrybutów.

https://aie24.pl/

Rzeczywistość wirtualna (VR) zaciera różnice między bezpośrednim i pośrednim dostępem do postrzeganej rzeczywistości. Doświadczenie VR jest jak doświadczenie Trumana Burbanka w The Truman Show, filmie, w którym iluzja stworzona przez dobrze zaprojektowane i dobrze zaprogramowane środowisko była nie do odróżnienia od rzeczywistości. Truman żył w tej społeczności (znanej jako Morskie Niebo) od urodzenia i zupełnie nie wiedział, że żyje w programie telewizyjnym. Jego rodzina, przyjaciele, sąsiedzi, krewni, pogoda i wszelkie inne przedmioty były częścią ogromnego, starannie zaprojektowanego studia telewizyjnego, skonfigurowanego tak, aby przypominało prawdziwy świat. Naturalna reakcja Trumana na tę wielką, ostateczną iluzję była nie tylko tymczasowa, ale utrzymywała się przez całe życie, aż do wieku dwudziestu dziewięciu lat, kiedy w końcu zdał sobie sprawę z fałszu swojego otoczenia. Co sprawiło, że Truman nigdy nie kwestionował tej sztucznej rzeczywistości? Sprzężenie percepcji i działania, zdolność przewidywania właściwości środowiska, wzajemność fizyczna i społeczna oraz nieświadomość innego świata mogą być prawdopodobnymi wyjaśnieniami. Poczucie obecności i wiarygodność działań zachodzących w środowisku kazały mu wierzyć, że Sea Haven to prawdziwy świat. Ten film oferuje scenę dla filozoficznego i empirycznego dialogu w celu zrozumienia rzeczywistości. Pozwala nam myśleć o problemach, takich jak poznawanie rzeczywistości. Skąd wiemy, że to, co postrzegamy i doświadczamy, jest rzeczywiście prawdziwe? Poszukiwania te intrygowały filozofów co najmniej od XVII wieku, kiedy to Kartezjusz zakwestionował wiarę i postrzeganie rzeczywistości. Coraz większe znaczenie i znaczenie VR w różnych dziedzinach, począwszy od rozrywki w grach, szkolenia wojskowego , praktyki klinicznej , poznania przestrzennego  do emocji , domagają się technologii VR, aby zrobić krok naprzód w celu zrealizowania „najlepszego wyświetlacza”. Ten ostateczny wyświetlacz jest urządzeniem konceptualnym (Sutherland, 1965), które ma na celu upodobnienie do rzeczywistości i zacieranie granic między fizycznym a sztucznym światem generowanym komputerowo, podobnie jak świat Trumana we wspomnianym filmie. Co ważniejsze, przewiduje przekraczanie fizycznej przestrzeni i otwiera okno do zbadania zdolności postrzegania-myślenia-i-działania, fenomenologicznego doświadczania uczuć i świadomości, poprzez umożliwienie kontroli, które sprzeciwiają się regułom fizycznej rzeczywistości, a jednocześnie tworzą poczucie obecność (Sutherland, 1965). Obecność jest zjawiskiem złożonym i obejmuje identyfikację i samolokację w przestrzeni przestrzenno-czasowej. „Identyfikacja” odnosi się do bycia obecnym jako ja. „Umiejscowienie siebie” w czasowym układzie odniesienia odnosi się do bycia obecnym jako „ja” w określonym czasie, od czasu do czasu, w tej samej chwili. Samo-lokalizacja w przestrzeni odnosi się do poczucia bycia obecnym w wirtualnym środowisku, jakby to była fizyczna rzeczywistość (Metzinger, 2018). Postrzegana rzeczywistość to spektrum, które rozciąga się od środowiska rzeczywistego do środowiska wirtualnego . Zdolność do wizualizacji, manipulacji i interakcji z wirtualnym środowiskiem określa stopień, w jakim postrzegamy i odczuwamy rzeczywistość. Postęp technologiczny w VR uświadamia nam kiedyś nie do pomyślenia koncepcje, takie jak poczucie sprawstwa i własności ciała , doświadczenie poza ciałem , halucynacje , iluzja wirtualnej dłoni, leczenie PTSD , leczenie schizofrenii , leczenie fobii i depresji , by wymienić tylko kilka. VR pozwala nam projektować  bardziej spersonalizowane, ekologicznie ważne, dyskretne, ściśle kontrolowane eksperymenty, które są niezbędne dla klinicznych ustawień terapeutycznych i obserwacji naukowych. Możliwość odtworzenia rzeczywistych scenariuszy, a jednocześnie możliwość prowadzenia badania z randomizowanymi, kontrolowanymi próbami, przewiduje więcej ilościowych i obiektywnych praktyk klinicznych i badań klinicznych w przyszłości. Obecnie diagnoza wszelkich zaburzeń psychicznych, w tym tak powszechnych jak depresja, opiera się głównie na badaniu klinicznym i subiektywnej ocenie zgłaszanych przez siebie objawów. Nie ma globalnie akceptowanych lub zatwierdzonych biomarkerów lub markerów psychologicznych/poznawczych stosowanych jako część kryteriów diagnostycznych (DSM-V i ICD-10) dla jakichkolwiek zaburzeń psychicznych (American Psychiatric Association, 2013). Interwencje psychoterapeutyczne i farmakologiczne oraz ich wpływ na obserwację stanu zdrowia pacjenta mają podobne protokoły postępowania jak procedura diagnostyczna.  Niedawno badanie konsorcjum  skupiające się na identyfikacji wielkich wyzwań związanych z zaburzeniami psychicznymi, neurologicznymi i związanymi z używaniem substancji (MNS) na całym świecie, zgłosiło 25 wielkich wyzwań związanych z zaburzeniami MNS w 2011 roku, z pomocą naukowców, zwolenników oraz klinicyści pracujący w ponad 60 krajach. Wśród tych 25 wielkich wyzwań, pierwsze miejsca zajęła potrzeba zidentyfikowania społecznych i biologicznych czynników ryzyka, opracowania biomarkerów, opracowania bardziej ekologicznej i opartej na dowodach interwencji oraz stworzenia bardziej opartych na kulturze metod. Sprawozdawczość subiektywna i badanie subiektywne utrudniają obserwacje kliniczne i ograniczają zakres stawienia czoła 25 wielkim wyzwaniom zaburzeń MNS, które opisali Collin i wsp. (2011). Subiektywne zgłaszanie opiera się na pamięci pacjentów, opartej na myślach samoobserwacji lub introspekcji oraz wyobraźni i oddala ich od uświadamiania sobie problemów ze zdrowiem psychicznym. Uświadamia również pacjentom postrzeganie i osąd innych, gdy dzielą się swoimi interoceptywnymi doświadczeniami, myślami i uczuciami z lekarzem. Jednak wirtualna rzeczywistość oferuje im bardziej spersonalizowane, ekologiczne i kontrolowane środowisko eksperymentalne. Ponadto pacjenci nie muszą polegać na swojej pamięci, introspekcji, odczuciach interoceptywnych, myślach i zachowaniu podczas interakcji ze środowiskiem VR. VR umożliwia dyskretną i bardziej obiektywną obserwację. Środowiska VR z ukierunkowaniem klinicznym mogą pomóc w badaniach psychologicznych i psychiatrycznych, a także sprawić, że praktyki kliniczne staną się bardziej humanitarne i mogą przyspieszyć rozwój markerów psychospołeczno-biologicznych zaproponowanych przez Narodowy Instytut Zdrowia Psychicznego w USA . Badania kliniczne oparte na VR miałyby kluczowe znaczenie w identyfikacji psychospołeczno-biologicznych czynników ryzyka. Pomogłoby to klinicystom zaprojektować programy wczesnej interwencji, aby opóźnić wystąpienie różnych zaburzeń psychicznych, takich jak depresja i lęk. Ponadto oferowałaby lepsze metody psychoterapeutyczne dla skuteczniejszego leczenia chorób psychicznych. W ten sposób VR daje wielką nadzieję na lepszą interwencję, monitorowanie i praktyki leczenia w przyszłości. Postępy w technologii VR sprawiają, że jest ona dostępna w przystępnych cenach i dostępna dla zwykłych ludzi. VR jest w trakcie rewolucyjnej transformacji, kolejnej rewolucji, jak komputery, które ostatecznie przeniosły się z konkretnych laboratoriów do domów zwykłych ludzi. Technologia VR zmieni grę i sprawi, że monitorowanie zdrowia psychicznego stanie się bardziej dostępne, łatwe i wygodne dla pacjentów, podobnie jak urządzenia do monitorowania zdrowia fizycznego, takie jak urządzenia do pomiaru ciśnienia krwi lub cukru. Tu omówiono badania kliniczne nad najnowocześniejszymi technologiami rzeczywistości wirtualnej. Podzielone jest na omówienie dwóch głównych technologii VR: rzeczywistości wirtualnej na głowie i rzeczywistości rozszerzonej. Najpierw omówimy najnowocześniejsze badania kliniczne VR i podkreślimy ograniczenia. W tej części omówione zostaną również przyszłe kierunki badań klinicznych VR. W części poświęconej badaniom klinicznym rzeczywistości rozszerzonej (AR) najpierw omówimy najnowocześniejsze badania kliniczne nad AR, a następnie omówimy ich ograniczenia i przyszłe kierunki. Sekcja dotycząca zdrowia psychicznego podkreśli ograniczenia obecnie trwających praktyk klinicznych i omówi zmianę punktu ciężkości z badania opartego na wywiadzie klinicznym na bardziej obiektywne, poznawcze, neurologiczne i społeczne perspektywy obserwacji klinicznych. Sekcja wirtualnej rzeczywistości omówi najpierw koncepcję rzeczywistości, a następnie podkreśli aktualne badania kliniczne VR. Ponadto w tej części omówione zostaną ograniczenia oparte na metodach obserwacji stosowanych w tych badaniach. Podkreśli potrzebę badań korelacji i przyczyn, koncentrujących się na poznawczych, biologicznych i społecznych perspektywach danego zaburzenia psychicznego. Ta sekcja stanowi znaczną część i stanowi podstawę dla sekcji rzeczywistości rozszerzonej. Sekcja AR omówi najpierw różnicę między VR a AR, a następnie zwróci uwagę na najnowocześniejsze badania kliniczne nad AR. Ograniczenia i przyszłe kierunki przedstawione w tej sekcji podkreślają odniesienia z badań klinicznych VR. Sekcja podsumowująca uzupełni krytyczne elementy każdej z tych sekcji.

https://aie24.pl/

Załóżmy, że kupujemy torebkę cukierków z limonki i wiśni od nowego producenta, którego proporcje smakowe są zupełnie nieznane; ułamek wiśni może wynosić od 0 do 1. W takim przypadku mamy kontinuum hipotez. Parametrem w tym przypadku, który nazywamy Θ , jest proporcja cukierków wiśniowych, a hipotezą jest h_Θ . (Proporcja cukierków z limonką wynosi tylko 1 – Θ.) Jeśli założymy, że wszystkie proporcje są a priori jednakowo prawdopodobne, wówczas podejście maksymalnego prawdopodobieństwa jest rozsądne. Jeśli modelujemy sytuację za pomocą sieci bayesowskiej, potrzebujemy tylko jednej zmiennej losowej, Flavour (smak losowo wybranego cukierka z torebki). Ma wartości wiśnia i limonka, gdzie prawdopodobieństwo pojawienia się wiśni wynosi Θ (patrz Rysunek 21.2(a)). Załóżmy teraz, że odpakujemy N cukierków, z których c to wiśnia, l`=N – c to limonka. Zgodnie z równaniem (21.3) prawdopodobieństwo tego konkretnego zbioru danych wynosi

Hipoteza maksymalnego prawdopodobieństwa jest podana przez wartość Θ, która maksymalizuje to wyrażenie. Ponieważ funkcja logarytmiczna jest monotoniczna, tę samą wartość uzyskuje się poprzez maksymalizację prawdopodobieństwa logarytmicznego:

(Biorąc logarytmy, redukujemy iloczyn do sumy danych, co zwykle łatwiej jest zmaksymalizować.) Aby znaleźć wartość maksymalnego prawdopodobieństwa Θ , różnicujemy L względem Θ i ustawiamy wynikowe wyrażenie na zero:

Zatem w języku angielskim hipoteza maksymalnego prawdopodobieństwa h_ML zakłada, że ​​rzeczywista proporcja cukierków wiśniowych w torebce jest równa obserwowanej proporcji w dotychczas nieopakowanych cukierkach! Wygląda na to, że wykonaliśmy dużo pracy, aby odkryć oczywistość. W rzeczywistości jednak opracowaliśmy jedną standardową metodę uczenia się parametrów maksymalnego prawdopodobieństwa, metodę o szerokim zastosowaniu:

1. Napisz wyrażenie określające prawdopodobieństwo danych jako funkcję parametru(ów).
2. Zapisz pochodną logarytmu wiarygodności dla każdego parametru.
3. Znajdź wartości parametrów takie, że pochodne są zerowe.

Najtrudniejszym krokiem jest zwykle ostatni. W naszym przykładzie było to trywialne, ale zobaczymy, że w wielu przypadkach musimy uciec się do algorytmów rozwiązań iteracyjnych lub innych technik optymalizacji numerycznej, jak opisano w rozdziale 4.2. (Będziemy musieli zweryfikować, czy macierz Hessów jest ujemnie określona.) Przykład ilustruje również istotny problem z ogólnie uczeniem się z maksymalnym prawdopodobieństwem: gdy zbiór danych jest na tyle mały, że niektóre zdarzenia jeszcze nie zostały zaobserwowane – na przykład brak cukierki wiśniowe – hipoteza maksymalnego prawdopodobieństwa przypisuje tym zdarzeniom zerowe prawdopodobieństwo. Aby uniknąć tego problemu, stosuje się różne sztuczki, takie jak inicjowanie liczników dla każdego zdarzenia na 1 zamiast 0. Spójrzmy na inny przykład. Załóżmy, że ten nowy producent cukierków chce dać konsumentowi małą wskazówkę i używa opakowań do cukierków w kolorze czerwonym i zielonym. Opakowanie dla każdego cukierka jest wybierane probabilistycznie, zgodnie z pewnym nieznanym rozkładem warunkowym, w zależności od smaku. Odpowiedni model prawdopodobieństwa pokazano na rysunku 21.2(b). Zauważ, że ma trzy parametry: Θ, Θ₁ i Θ₂. Dzięki tym parametrom prawdopodobieństwo zobaczenia, powiedzmy, cukierka wiśniowego w zielonym opakowaniu można uzyskać ze standardowej semantyki dla sieci bayesowskich

Teraz odwijamy N cukierków, z których c to wiśnia, a l to limonka. Liczba opakowań jest następująca: r_c cukierków wiśniowych ma czerwone opakowania, a gc zielone, natomiast r_l cukierków limonkowych ma czerwone, a g_l zielone. Prawdopodobieństwo danych jest podane przez

Wygląda to okropnie, ale logarytmowanie pomaga:

Korzyść z rejestrowania logów jest oczywista: prawdopodobieństwo logarytmu jest sumą trzech terminów, z których każdy zawiera jeden parametr. Kiedy weźmiemy pochodne względem każdego parametru i ustawimy je na zero, otrzymamy trzy niezależne równania, z których każde zawiera tylko jeden parametr:

Rozwiązanie dla Θ jest takie samo jak poprzednio. Rozwiązaniem dla 1, prawdopodobieństwa, że cukierek wiśniowy ma czerwone opakowanie, jest obserwowana frakcja cukierków wiśniowych z czerwonym opakowaniem, podobnie dla 2. Wyniki te są bardzo pocieszające i łatwo zauważyć, że można je rozszerzyć na dowolną sieć bayesowską, której prawdopodobieństwa warunkowe są reprezentowane w postaci tabel. Najważniejszą kwestią jest to, że przy kompletnych danych problem uczenia się parametrów maksymalnego prawdopodobieństwa dla sieci bayesowskiej rozkłada się na oddzielne problemy uczenia się, po jednym dla każdego parametru. Drugą kwestią jest to, że wartości parametrów dla zmiennej, biorąc pod uwagę jej rodziców, są po prostu obserwowanymi częstotliwościami wartości zmiennych dla każdego ustawienia wartości rodzicielskich. Tak jak poprzednio, musimy uważać, aby uniknąć zer, gdy zestaw danych jest mały.

https://aie24.pl/

Sztuczna inteligencja była rewolucją, która zmieniła nasz świat na każdą skalę. Opieka zdrowotna jest jedną z najważniejszych usług w każdym kraju, a wiele operacji chirurgicznych odbywa się dziś z udziałem sztucznej inteligencji. Wydajność, szybkość i precyzja odgrywają ważną rolę w każdej czynności medycznej, czy to chirurgii, przeszczepie, czy nawet obrazowaniu medycznym. Zakres błędu ludzkiego jest zawsze ryzykiem w każdej działalności medycznej, a posiadany sprzęt nie zawsze jest oszczędny i często również ryzykowny. Sztuczna inteligencja zaznacza wszystkie właściwe pola i ma potencjał, aby zmienić branżę medyczną. Techniki diagnostyki obrazów wykorzystujące sztuczną inteligencję zmniejszają intensywność promieni rentgenowskich, na które pacjent musi być wystawiony, i dają porównywalnie bardziej precyzyjne wyniki niż jakakolwiek z konwencjonalnych technik, takich jak CAT, MRI lub RTG. Operacje wymagają dużego skupienia i precyzji, których brak, niezależnie od doświadczenia lekarza, prowadzi do błędów. Chirurdzy-robotycy znacznie się rozwinęli i są bliscy przyjęcia sztucznej inteligencji, aby działała wydajniej. Stworzenie opartej na chmurze sztucznej inteligencji i robotów obsługujących głębokie uczenie, które są szkolone na niezliczonych danych i działają na podstawie spostrzeżeń lekarzy, otwiera drzwi do nieskończonych możliwości w branży opieki zdrowotnej.

https://aie24.pl/

Ogólne zadanie uczenia się modelu prawdopodobieństwa na podstawie danych, które zakłada się, że są generowane z tego modelu, nazywa się estymacją gęstości. (Termin stosowany pierwotnie do funkcji gęstości prawdopodobieństwa dla zmiennych ciągłych, ale obecnie jest używany również dla rozkładów dyskretnych). Estymacja gęstości jest formą uczenia się bez nadzoru. W tej sekcji omówiono najprostszy przypadek, w którym mamy pełne dane. Dane są kompletne, gdy każdy punkt danych zawiera wartości dla każdej zmiennej w uczonym modelu prawdopodobieństwa. Skupiamy się na uczeniu parametrów – znajdowaniu parametrów numerycznych dla modelu prawdopodobieństwa, którego struktura jest ustalona. Na przykład możemy być zainteresowani poznaniem prawdopodobieństw warunkowych w sieci bayesowskiej o określonej strukturze. Przyjrzymy się również pokrótce problemowi struktury uczenia się oraz nieparametrycznej estymacji gęstości.

 

https://aie24.pl/

Genom ludzki ma 3 miliardy par zasad. Są one analizowane przez sztuczną inteligencję, która wykrywa zmiany w genomach nawet w pojedynczych lokalizacjach zasad. Pomaga to w diagnozowaniu, leczeniu, a w przyszłości zapobieganiu zaburzeniom genetycznym. Terapia genowa, tj. zastąpienie zmutowanych genów powodujących chorobę przez funkcjonalny gen, może być możliwy dzięki AI .

 

https://aie24.pl/

Kluczowymi pojęciami tu, są dane i hipotezy. Tutaj dane są dowodem, to znaczy egzemplarzami niektórych lub wszystkich zmiennych losowych opisujących domenę. Hipotezy przedstawione w tym rozdziale to probabilistyczne teorie działania dziedziny, w tym teorie logiczne jako przypadek szczególny. Rozważ prosty przykład. Nasze ulubione cukierki-niespodzianki występują w dwóch smakach: wiśniowym (mniam) i limonkowym (ugh). Producent ma swoiste poczucie humoru i niezależnie od smaku zawija każdy cukierek w to samo nieprzezroczyste opakowanie. Cukierek sprzedawany jest w bardzo dużych torebkach, których znanych jest pięć rodzajów – znowu nie do odróżnienia z zewnątrz:

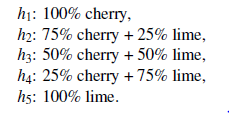
Biorąc pod uwagę nową torebkę cukierków, zmienna losowa H (dla hipotezy) oznacza rodzaj torebki, z możliwymi wartościami od h₁ do h5. Oczywiście H nie można zaobserwować bezpośrednio. Gdy kawałki cukierka są otwierane i sprawdzane, ujawniają się dane-D₁, D₂, …, D_N, gdzie każdy D_i jest zmienną losową z możliwymi wartościami wiśni i limonki. Podstawowym zadaniem stojącym przed agentem jest przewidzenie smaku kolejnego cukierka. Ten scenariusz, mimo pozornej banalności, wprowadza wiele istotnych kwestii. Agent naprawdę musi wywnioskować teorię swojego świata, aczkolwiek bardzo prostą. Uczenie bayesowskie po prostu oblicza prawdopodobieństwo każdej hipotezy na podstawie danych i dokonuje na tej podstawie przewidywań. Oznacza to, że prognozy są dokonywane przy użyciu wszystkich hipotez ważonych ich prawdopodobieństwem, a nie tylko jednej „najlepszej” hipotezy. W ten sposób uczenie się sprowadza się do wnioskowania probabilistycznego. Niech D reprezentuje wszystkie dane, z obserwowaną wartością d. Kluczowe wielkości w podejściu bayesowskim to uprzednia hipoteza P(hi) oraz prawdopodobieństwo danych w ramach każdej hipotezy, P(d|h_i). Prawdopodobieństwo każdej hipotezy uzyskuje się z reguły Bayesa:

 

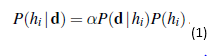
Załóżmy teraz, że chcemy przewidzieć nieznaną wielkość X. Wtedy mamy

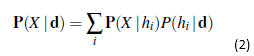
gdzie każda hipoteza określa rozkład prawdopodobieństwa względem X. Równanie to pokazuje, że predykcje są średnimi ważonymi predykcji poszczególnych hipotez, gdzie waga P(h_i|d) jest proporcjonalna do prawdopodobieństwa uprzedniego hi i jego stopnia dopasowania, zgodnie z Równaniem (1). Same hipotezy są zasadniczo „pośrednikami” między surowymi danymi a przewidywaniami. Dla naszego przykładu ze słodyczami przyjmiemy na razie, że uprzedni rozkład nad h₁,…,h₅ jest podane przez <0.1,0.2,0.4,0.2,0.1>, jak reklamuje producent. Prawdopodobieństwo danych jest obliczane przy założeniu, że obserwacje są i.i.d. , aby

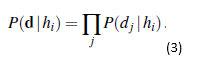
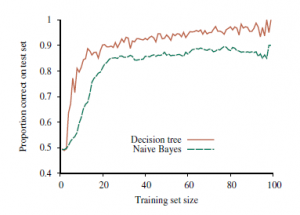
Załóżmy na przykład, że torebka jest w rzeczywistości całkowicie limonkowa (h₅), a pierwsze 10 cukierków to w całości limonka; wtedy P(d|h₃) wynosi 0.5¹⁰, ponieważ połowa cukierków w torebce h₃ to wapno. Rysunek (a) pokazuje, jak zmieniają się prawdopodobieństwo a posteriori pięciu hipotez, gdy obserwuje się sekwencję 10 cukierków z wapnem.

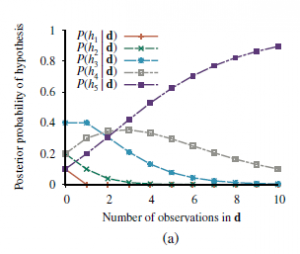
Zauważ, że prawdopodobieństwa zaczynają się od poprzednich wartości, więc h₃ jest początkowo najbardziej prawdopodobnym wyborem i pozostaje takie po rozpakowaniu 1 cukierka z limonką. Po rozpakowaniu 2 cukierków z limonką, najprawdopodobniej h₄; po 3 lub więcej, najbardziej prawdopodobne jest h₅ (przerażająca torebka z limonką). Po 10 z rzędu jesteśmy dość pewni naszego losu. Rysunek (b) pokazuje przewidywane prawdopodobieństwo, że następnym cukierkiem będzie limonka, na podstawie równania (2).

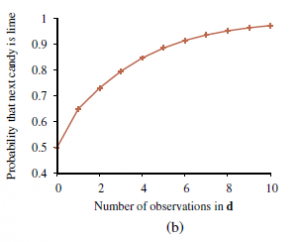
Jak oczekiwalibyśmy, wzrasta ona monotonicznie do 1. Przykład pokazuje, że przewidywanie bayesowskie ostatecznie zgadza się z prawdziwą hipotezą. Jest to charakterystyczne dla uczenia bayesowskiego. W przypadku dowolnego ustalonego a priori, które nie wyklucza prawdziwej hipotezy, prawdopodobieństwo a posteriori jakiejkolwiek fałszywej hipotezy w pewnych warunkach technicznych ostatecznie zniknie. Dzieje się tak po prostu dlatego, że prawdopodobieństwo generowania „nietypowych” danych w nieskończoność jest znikomo małe. Co ważniejsze, przewidywanie bayesowskie jest optymalne, niezależnie od tego, czy zbiór danych jest mały czy duży. Biorąc pod uwagę wcześniejszą hipotezę, oczekuje się, że każda inna prognoza będzie poprawna rzadziej. Oczywiście optymalność uczenia bayesowskiego ma swoją cenę. W przypadku rzeczywistych problemów z uczeniem się przestrzeń hipotez jest zwykle bardzo duża lub nieskończona, jak widzieliśmy w rozdziale 19. W niektórych przypadkach sumowanie w równaniu (2) (lub całkowanie w przypadku ciągłym) można przeprowadzić w sposób praktyczny, ale w w większości przypadków musimy uciekać się do metod przybliżonych lub uproszczonych. Bardzo powszechnym przybliżeniem – takim, które jest zwykle przyjmowane w nauce – jest dokonywanie przewidywań na podstawie jednej najbardziej prawdopodobnej hipotezy – to znaczy hi maksymalizuje P(h_i|d). Jest to często nazywane hipotezą maksimum a posteriori lub MAP (wymawiane „em-ay-pee”). Prognozy wykonane zgodnie z hipotezą MAP h_MAP są w przybliżeniu bayesowskie do tego stopnia, że ​​P(X|d) ≈ P(X |h_MAP). W naszym przykładzie cukierków h_MAP=h₅ po trzech cukierkach z limonką z rzędu, więc uczeń MAP przewiduje, że czwarty cukierek to limonka z prawdopodobieństwem 1,0 – o wiele bardziej niebezpieczna prognoza niż przewidywanie bayesowskie 0,8 pokazane na rysunku (b). . W miarę napływu większej ilości danych prognozy MAP i Bayesa stają się coraz bliższe, ponieważ konkurencja dla hipotezy MAP staje się coraz mniej prawdopodobna. Chociaż ten przykład tego nie pokazuje, znajdowanie hipotez MAP jest często znacznie łatwiejsze niż uczenie bayesowskie, ponieważ wymaga rozwiązania problemu optymalizacji zamiast dużego problemu sumowania (lub integracji). Zarówno w uczeniu bayesowskim, jak i uczeniu MAP ważną rolę odgrywa hipoteza poprzedzająca P(h_i). W rozdziale 19 widzieliśmy, że nadmierne dopasowanie może wystąpić, gdy przestrzeń hipotez jest zbyt wyrazista, to znaczy, gdy zawiera wiele hipotez, które dobrze pasują do zbioru danych. Metody uczenia bayesowskiego i MAP wykorzystują wcześniejsze, aby ukarać złożoność. Zazwyczaj bardziej złożone hipotezy mają niższe prawdopodobieństwo a priori – po części dlatego, że jest ich tak wiele. Z drugiej strony bardziej złożone hipotezy mają większą zdolność dopasowania danych. (W skrajnym przypadku tabela przeglądowa może dokładnie odtworzyć dane). Dlatego wcześniejsza hipoteza zawiera kompromis między złożonością hipotezy a jej stopniem dopasowania do danych. Efekt tego kompromisu widać najwyraźniej w przypadku logicznym, w którym H zawiera tylko hipotezy deterministyczne (takie jak h1, który mówi, że każdy cukierek jest wiśnią). W takim przypadku P(d|h_i) wynosi 1, jeśli hi jest spójne, a 0 w przeciwnym razie. Patrząc na równanie (1), widzimy, że h_MAP będzie wtedy najprostszą teorią logiczną, która jest zgodna z danymi. Dlatego nauka J maksymalnie a posteriori stanowi naturalne ucieleśnienie brzytwy Ockhama. Inny wgląd w kompromis między złożonością a stopniem dopasowania można uzyskać, logarytmując równanie (1). Wybranie hMAP do maksymalizacji P(djhi)P(hi) jest równoznaczne z minimalizacją

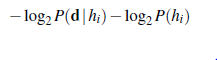
Używając związku między kodowaniem informacji a prawdopodobieństwem,  widzimy, że wyraz -log₂ P(h_i) jest równy liczbie bitów wymaganych do sprecyzowania hipotezy hi. Co więcej, -log₂ P(d|h_i) to dodatkowa liczba bitów wymagana do sprecyzowania danych przy założeniu hipotezy. (Aby to zobaczyć, weź pod uwagę, że nie są wymagane żadne bity, jeśli hipoteza dokładnie przewiduje dane – jak w przypadku h5 i sznurka cukierków z limonki – i log₂ 1=0.) Dlatego uczenie MAP polega na wyborze hipotezy, która zapewnia maksymalną kompresję dane. Do tego samego zadania odnosi się bardziej bezpośrednio metoda uczenia się z minimalną długością opisu, czyli MDL. Podczas gdy uczenie MAP wyraża prostotę, przypisując wyższe prawdopodobieństwa prostszym hipotezom, MDL wyraża to bezpośrednio, licząc bity w binarnym kodowaniu hipotez i danych. Ostatecznym uproszczeniem jest założenie jednolitego a priori nad przestrzenią hipotez. W takim przypadku uczenie się MAP sprowadza się do wybrania hi, które maksymalizuje P(d|hi). Nazywa się to hipotezą maksymalnego prawdopodobieństwa, h_ML. Nauka maksymalnego prawdopodobieństwa jest bardzo powszechna w statystyce, dyscyplinie, w której wielu badaczy nie ufa subiektywnej naturze hipotez a priori. Jest to rozsądne podejście, gdy nie ma powodu, aby a priori przedkładać jedną hipotezę nad inną — na przykład, gdy wszystkie hipotezy są jednakowo złożone. Gdy zestaw danych jest duży, wcześniejszy rozkład nad hipotezami jest mniej ważny – dowody z danych są wystarczająco mocne, aby zasypać wcześniejszy rozkład hipotezami. Oznacza to, że uczenie z maksymalnym prawdopodobieństwem jest dobrym przybliżeniem do uczenia bayesowskiego i MAP z dużymi zestawami danych, ale ma problemy (jak zobaczymy) z małymi zestawami danych.

https://aie24.pl/

Elektroniczna dokumentacja medyczna zebrana podczas leczenia ciąży jest wprowadzana do systemu EMR opartego na sztucznej inteligencji, który powiadamia lekarza, przekazując cenne informacje zwrotne i wzorce umożliwiające dostosowanie leczenia każdego pacjenta. Wykrywanie raka szyjki macicy i przedwczesnego zagrożenia ciężarnej matki, informacje o stanie zdrowia, wieku itp. płodu to tylko niektóre z wielu zadań, jakie może wykonać sztuczna inteligencja.

 

https://aie24.pl/

Zbadaliśmy różne sposoby, w jakie wcześniejsza wiedza może pomóc agentowi w uczeniu się na nowych doświadczeniach. Ponieważ znaczna część dotychczasowej wiedzy jest wyrażana w kategoriach modeli relacyjnych, a nie modeli opartych na atrybutach, omówiliśmy również systemy, które umożliwiają uczenie się modeli relacyjnych. Ważne punkty to:

• Wykorzystanie wcześniejszej wiedzy w uczeniu się prowadzi do obrazu skumulowanego uczenia się, w którym uczący się agenci poprawiają swoją zdolność uczenia się w miarę zdobywania większej wiedzy.
• Wcześniejsza wiedza pomaga w uczeniu się, eliminując skądinąd spójne hipotezy i „uzupełniając” wyjaśnienia przykładów, co pozwala na stawianie krótszych hipotez. Te wkłady często skutkują szybszym uczeniem się z mniejszej liczby przykładów.
• Zrozumienie różnych ról logicznych odgrywanych przez wcześniejszą wiedzę, wyrażonych przez ograniczenia implikacji, pomaga zdefiniować różnorodne techniki uczenia się.
• Uczenie się oparte na wyjaśnieniach (EBL) wyodrębnia ogólne zasady z pojedynczych przykładów, wyjaśniając przykłady i uogólniając wyjaśnienie. Zapewnia dedukcyjną metodę przekształcania wiedzy o podstawowych zasadach w użyteczną, wydajną wiedzę specjalistyczną o specjalnym przeznaczeniu.
• Uczenie się oparte na istotności (RBL) wykorzystuje wcześniejszą wiedzę w formie określeń do identyfikacji odpowiednich atrybutów, tym samym generując zmniejszoną przestrzeń dla hipotez i przyspieszając uczenie się. RBL pozwala również na dedukcyjne uogólnienia z pojedynczych przykładów.
• Uczenie indukcyjne oparte na wiedzy (KBIL) znajduje hipotezy indukcyjne, które wyjaśniają zbiory obserwacji za pomocą wiedzy podstawowej.
• Techniki programowania logiki indukcyjnej (ILP) wykonują KBIL na wiedzy wyrażonej w logice pierwszego rzędu. Metody ILP mogą uczyć się wiedzy relacyjnej, której nie można wyrazić w systemach opartych na atrybutach.
• ILP można przeprowadzić z zastosowaniem podejścia odgórnego polegającego na dopracowaniu bardzo ogólnej zasady lub oddolnego podejścia polegającego na odwróceniu procesu dedukcyjnego.
• Metody ILP w naturalny sposób generują nowe predykaty, za pomocą których można wyrażać nowe zwięzłe teorie i obiecujące jako uniwersalne systemy tworzenia teorii naukowych.