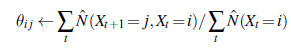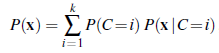Miesiąc: listopad 2022

https://aie24.pl/

Nasze ostateczne zastosowanie EM obejmuje poznanie prawdopodobieństw przejścia w ukrytych modelach Markowa (HMM). Przypomnijmy , że ukryty model Markowa może być reprezentowany przez dynamiczną sieć Bayesa z pojedynczą dyskretną zmienną stanu, jak pokazano na rysunku 

Każdy punkt danych składa się z sekwencji obserwacji o skończonej długości, więc problemem jest poznanie prawdopodobieństw przejścia ze zbioru sekwencji obserwacji (lub tylko jednej długiej sekwencji). Widzieliśmy już, jak uczyć się sieci Bayesa, ale jest to komplikacja: w sieciach Bayesa każdy parametr jest inny; z drugiej strony w ukrytym modelu Markowa poszczególne prawdopodobieństwa przejścia ze stanu i do stanu j w czasie t, θ_ijt =P(X_t+1= j|X_t =i), są powtarzane w czasie, czyli θ_ijt = θ_ij dla wszystkich t. Aby oszacować prawdopodobieństwo przejścia ze stanu i do stanu j, po prostu obliczamy oczekiwany odsetek przypadków przejścia systemu do stanu j w stanie i:

Oczekiwane liczby są obliczane przez algorytm anHMMinference. Algorytm naprzód-wstecz przedstawiony  można bardzo łatwo zmodyfikować, aby obliczyć niezbędne prawdopodobieństwa. Ważną kwestią jest to, że wymagane prawdopodobieństwa uzyskuje się poprzez wygładzanie, a nie filtrowanie. Filtrowanie daje rozkład prawdopodobieństwa aktualnego stanu, biorąc pod uwagę przeszłość, ale wygładzanie daje rozkład podany wszelkimi dowodami, łącznie z tym, co dzieje się po wystąpieniu określonego przejścia. Dowody w sprawie o morderstwo są zwykle uzyskiwane po dokonaniu przestępstwa (tj. przejściu ze stanu i do stanu j).

https://aie24.pl/

Opracowano inteligentne urządzenia monitorujące do zarządzania elektrowniami słonecznymi za pomocą IoT: czujniki zapewniające analizę danych, sterowanie SPV i wykrywanie usterek (Hiszpania, 2017). Stworzono zintegrowany system informatyczny do monitorowania i zarządzania środowiskiem, wykorzystując najnowsze technologie, takie jak IoT, geoinformatyka, big data i cloud computing . IoT jest wykorzystywane przez wielu badaczy do oceny, zarządzania i monitorowania potencjału słonecznego z wykorzystaniem teledetekcji, GIS, dużych zbiorów danych i przetwarzania w chmurze . Usługi Aeris IoT zapewniają rozwiązania do konserwacji projektów energii słonecznej z wykorzystaniem łączności GSM i CDMA, w tym 2G, 3G i 4G LTE . Pomaga to w analizowaniu i przetwarzaniu aktualizacji i danych projektu fotowoltaicznego w czasie rzeczywistym. Tego typu usługi pomagają w uzyskaniu dokładnych i szybkich informacji z projektu M2M i IoT. Dane online dotyczące natężenia promieniowania słonecznego zostały wykorzystane przez wielu badaczy do przeprowadzenia oceny potencjału słonecznego, analizy energii i kosztów. Do przeprowadzenia analizy natężenia promieniowania słonecznego naukowcy wykorzystali dane o natężeniu promieniowania słonecznego (NASA) oraz dane dotyczące użytkowania gruntów . Lefevre i inni wyprowadzili podstawową zasadę Heliosat-II . Równanie zdefiniowało indeks zachmurzenia, n, jako wartość natężenia napromienienia wykrytego przez czujnik w stosunku do wartości natężenia napromienienia piksela przy ziemi. Jeśli nie ma różnicy, to jest to związane z przejrzystością atmosfery.

ρ^t(i,j) jest współczynnikiem odbicia lub pozornym albedo obserwowanym przez czujnik w przestrzeni kosmicznej dla czasu t i piksela (I,j):  

gdzie L^t(i,j) to obserwowana radiancja; ρ^t_cloud  to pozorne albedo nad najjaśniejszymi chmurami, a ρ_g^t (i,j) to pozorne albedo nad ziemią pod czystym niebem. Zhang i Grijalva opracowali opartą na danych metodologię identyfikacji, weryfikacji i szacowania mieszkaniowych instalacji fotowoltaicznych przy użyciu algorytmu punktu zmiany w celu wybrania niefunkcjonalnego wykorzystania energii i zweryfikowali za pomocą listy permutacji ze współczynnikiem rang Spearmana. Obliczyli obciążenie PV przy użyciu lokalnego zestawu danych meteorologicznych. Spanias  opracował ramy do zarządzania projektami słonecznymi za pomocą czujników IoT. Zademonstrował ramy zarządzania i dostarczania mobilnej analityki, umożliwienia sterowania elektrownią słoneczną, kodu oprogramowania do wykrywania i zarządzania usterkami, optymalizacji mocy i redukcji stanów nieustalonych falownika za pomocą filtra Kalmana, przetwarzania sygnału, sieci neuronowej i metod cyfrowego przetwarzania obrazu.

https://aie24.pl/

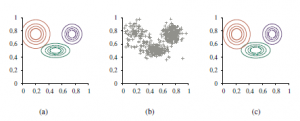
Aby nauczyć się sieci bayesowskiej z ukrytymi zmiennymi, stosujemy te same spostrzeżenia, które działały w przypadku mieszanek Gaussa. Rysunek(a)

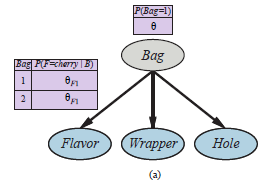
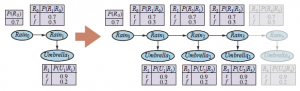
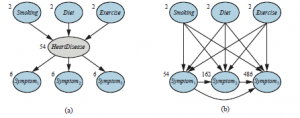
przedstawia sytuację, w której zmieszano dwie torebki cukierków. Cukierki są opisane trzema cechami: oprócz Smaku i Opakowania, niektóre cukierki mają otwór w środku, a niektóre nie. Rozkład cukierków w każdej torebce jest opisany przez naiwny model Bayesa: cechy są niezależne dla danej torebki, ale rozkład prawdopodobieństwa warunkowego dla każdej cechy zależy od torebki. Parametry są następujące: θ jest prawdopodobieństwem a priori, że cukierek pochodzi z Bag 1; θ_F1 i θ_F2 to prawdopodobieństwa, że ​​smak jest wiśniowy, biorąc pod uwagę, że cukierek pochodzi odpowiednio z Torebki 1 lub Torebki 2; θ_W1 i θ_W2 podają prawdopodobieństwa, że ​​opakowanie jest czerwone; a θ_H1 i θ_H2 dają prawdopodobieństwo, że cukierek ma dziurkę. Ogólny model to model mieszany: ważona suma dwóch różnych rozkładów, z których każdy jest iloczynem niezależnych rozkładów jednowymiarowych. (W rzeczywistości możemy również modelować mieszaninę Gaussów jako sieć bayesowską, jak pokazano na rysunku (b).)

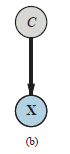
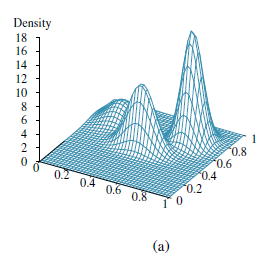
Na rysunku torebka jest zmienną ukrytą, ponieważ po zmieszaniu cukierków już nie wiedzieć, z której torby pochodzi każdy cukierek. Czy w takim razie możemy odzyskać opisy dwóch torebek, obserwując cukierki z mieszanki? Przejdźmy przez iterację EM dla tego problemu. Najpierw spójrzmy na dane. Wygenerowaliśmy 1000 próbek z modelu, którego prawdziwe parametry są następujące:

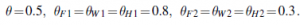
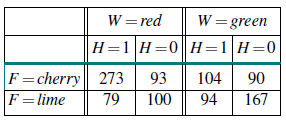
Oznacza to, że cukierki z równym prawdopodobieństwem pochodzą z obu toreb; pierwszy to głównie wiśnia z czerwonymi obwoluty i dziurkami; drugi to głównie limonka z zielonymi opakowaniami i bez dziur. Liczba ośmiu możliwych rodzajów cukierków jest następująca:

Zaczynamy od inicjalizacji parametrów. Dla uproszczenia numerycznego wybieramy arbitralnie

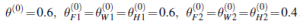
Najpierw popracujmy nad parametrem θ. W przypadku w pełni obserwowalnym oszacowalibyśmy to bezpośrednio na podstawie zaobserwowanej liczby cukierków z torebek 1 i 2. Ponieważ torebka jest zmienną uk rytą, zamiast tego obliczamy oczekiwane liczby. Oczekiwana liczba 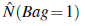 jest sumą prawdopodobieństwa, że cukierek pochodzi z woreczka 1 dla wszystkich cukierków.

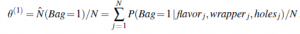
Prawdopodobieństwa te można obliczyć za pomocą dowolnego algorytmu wnioskowania dla sieci bayesowskich. W przypadku naiwnego modelu Bayesa, takiego jak ten w naszym przykładzie, możemy wnioskować „ręcznie”, korzystając z reguły Bayesa i stosując warunkową niezależność:

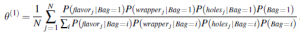
Stosując tę formułę do, powiedzmy, 273 cukierków wiśniowych w czerwonych opakowaniach z dziurkami, otrzymujemy wkład w wysokości

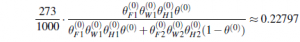
Kontynuując z pozostałymi siedmioma rodzajami cukierków w tabeli liczebności, otrzymujemy θ⁽¹⁾=0:6124. Rozważmy teraz inne parametry, takie jak θ_F1. W przypadku w pełni obserwowalnym oszacowalibyśmy to bezpośrednio na podstawie zaobserwowanej liczby cukierków wiśniowych i limonkowych z torebki 1. Oczekiwana liczba cukierków wiśniowych z torebki 1 jest dana wzorem

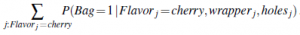
Ponownie, prawdopodobieństwa te można obliczyć dowolnym algorytmem sieci Bayesa. Kończąc ten proces otrzymujemy nowe wartości wszystkich parametrów:

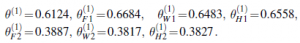
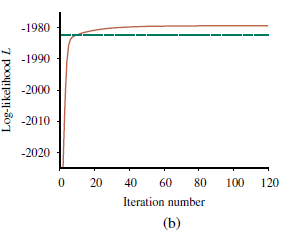
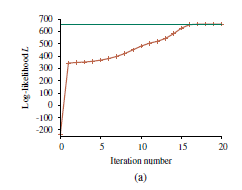
Oznacza to, że aktualizacja poprawia samo prawdopodobieństwo około e²³ ≈ 10¹⁰. Przy dziesiątej iteracji wyuczony model jest lepiej dopasowany niż model oryginalny (L= -1982.214). Następnie postęp staje się bardzo powolny. Nie jest to rzadkością w przypadku EM, a wiele praktycznych systemów łączy EM z algorytmem gradientowym, takim jak Newton-Raphson  w ostatniej fazie uczenia się. Ogólna lekcja z tego przykładu jest taka, że ​​aktualizacje parametrów dla uczenia sieci bayesowskiej z ukrytymi zmiennymi są bezpośrednio dostępne z wyników wnioskowania na każdym przykładzie. Ponadto dla każdego parametru potrzebne są tylko lokalne prawdopodobieństwa a posteriori. Tutaj „lokalny” oznacza, że ​​tablicę prawdopodobieństwa warunkowego (CPT) dla każdej zmiennej X_i można nauczyć się z prawdopodobieństw a posteriori obejmujących tylko Xi i jego rodziców U_i. Definiując θ_ijk jako parametr CPT P(X_i=x_ij |U_i=uik), aktualizacja jest podawana przez znormalizowane oczekiwane liczby w następujący sposób:

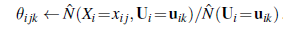
Oczekiwane liczby uzyskuje się przez zsumowanie przykładów, obliczenie prawdopodobieństw P(X_i=x_ij,U_i=u_ik) dla każdego przy użyciu dowolnego algorytmu wnioskowania sieci Bayesa. W przypadku dokładnych algorytmów – w tym eliminacji zmiennych – wszystkie te prawdopodobieństwa można uzyskać bezpośrednio jako produkt uboczny standardowego wnioskowania, bez konieczności wykonywania dodatkowych obliczeń związanych z uczeniem się. Ponadto informacje potrzebne do nauki są dostępne lokalnie dla każdego parametru. Cofając się trochę, możemy pomyśleć o tym, co robi algorytm EM w tym przykładzie jako odzyskiwanie siedmiu parametrów ( θ, θ_F1, θ_W1 , θ_H1, θ_F2 , θ_W2, θ_H2) z siedmiu (2³ -1) obserwowane liczebności w danych. (Ósma liczba jest ustalona przez fakt, że liczby sumują się do 1000). Gdyby każdy cukierek był opisany dwoma atrybutami, a nie trzema (powiedzmy, pomijając dziury), mielibyśmy pięć parametrów (θ, θ_{F1 ,} θ_W1 , θ_F2 , θ_W2), ale tylko trzy (2²-1) zaobserwowane zliczenia. W takim przypadku nie jest możliwe odzyskanie masy mieszanki lub właściwości dwóch zmieszanych ze sobą worków. Mówimy, że model dwuatrybutowy nie jest identyfikowalny. Identyfikowalność w sieciach bayesowskich to trudna kwestia. Zauważ, że nawet przy trzech atrybutach i siedmiu zliczeniach nie możemy jednoznacznie odtworzyć modelu, ponieważ istnieją dwa obserwacyjnie równoważne modele z odwróconą zmienną Bag. W zależności od tego, jak parametry są inicjowane, EM zbiegnie się albo do modelu, w którym torebka 1 zawiera głównie wiśnie, a torebka 2 głównie limonkę, lub odwrotnie. Tego rodzaju, jeśli nieidentyfikowalność jest nieunikniona w przypadku zmiennych, które nigdy nie są obserwowane.

https://aie24.pl/

Internet rzeczy (IoT) umożliwia maszynom komunikowanie się i wymianę informacji między sobą bez minimalnej liczby ludzkich mediatorów. IoT odgrywa ważną rolę w przekazywaniu informacji i podejmowaniu decyzji. Pomaga w teledetekcji, rejestrując miejsce z odległej lokalizacji i wysyłając dane do przetwarzania użytkownikom. Termin „Internet przedmiotów” został ukuty przez Kevina Ashtona w 1999 roku podczas prezentacji pracy Procter & Gamble (P&G). IoT zajmuje się czujnikami i urządzeniami fizycznymi podłączonymi do Internetu. Jeśli urządzenie nie jest teraz połączone z Internetem, zostanie połączone z Internetem w przyszłości. Komunikacja maszyna-maszyna (M2M) to połączenie pomiędzy różnymi typami maszyn, takimi jak komputer stacjonarny, skaner, mysz itp. Ta M2M jest podzbiorem IoT. W obu przypadkach M2M i IoT nie mogą się wzajemnie zastępować. IoT to nadzbiór połączonych maszyn . Informacje z satelitów, panelu słonecznego i czujników są przesyłane do analityki za pośrednictwem Internetu. Cztery kluczowe elementy IoT to ludzie, rzeczy, dane i procesy. Ludzie tutaj odnoszą się do punktów końcowych podłączonych do Internetu, aby udostępniać informacje, takie jak na przykład czujniki teledetekcji, zdrowia i kondycji. Te wyodrębnione funkcje zostały wykorzystane do oszacowania powierzchni użytkowej do zainstalowania panelu SPV. Pytania badawcze, które zostały sformułowane w celu sprawdzenia przydatności tych badań, obejmują: Czy w tym miejscu jest możliwe zainstalowanie sprzętu do wytwarzania energii słonecznej? oraz Ile potencjału słonecznego jest dostępne przy użyciu nachylonego GHI z piranometru? Oszacowanie najlepszych praktyk zarządzania konserwacją elektrowni słonecznych jest również przedmiotem badań.

https://aie24.pl/

Nienadzorowane grupowanie to problem rozróżniania wielu kategorii w kolekcji obiektów. Problem nie jest nadzorowany, ponieważ nie podano etykiet kategorii. Załóżmy na przykład, że rejestrujemy widma stu tysięcy gwiazd; czy istnieją różne typy gwiazd ujawniane przez widma, a jeśli tak, to ile typów i jakie są ich cechy charakterystyczne? Wszyscy znamy terminy takie jak „czerwony olbrzym” i „biały karzeł”, ale gwiazdy nie noszą tych etykiet na kapeluszach – astronomowie musieli wykonywać nienadzorowane grupowanie, aby zidentyfikować te kategorie. Inne przykłady obejmują identyfikację gatunków, rodzajów, rzędów, gromady itd. w taksonomii Linneusza oraz tworzenie naturalnych rodzajów dla zwykłych przedmiotów. Nienadzorowane klastrowanie zaczyna się od danych. Rysunek 21.12(b) przedstawia 500 punktów danych, z których każdy określa wartości dwóch ciągłych atrybutów. Punkty danych mogą odpowiadać gwiazdom, a atrybuty mogą odpowiadać intensywnościom widmowym przy dwóch określonych częstotliwościach. Następnie musimy zrozumieć, jaki rodzaj rozkładu prawdopodobieństwa mógł wygenerować dane. Grupowanie zakłada, że ​​dane są generowane z rozkładu mieszaniny P. Taki rozkład ma k składników, z których każdy jest rozkładem sam w sobie. Punkt danych jest generowany przez wybranie najpierw składnika, a następnie wygenerowanie próbki z tego składnika. Niech zmienna losowa C oznacza składnik o wartościach 1,…,k; wtedy rozkład mieszaniny jest podany przez

gdzie x odnosi się do wartości atrybutów dla punktu danych. W przypadku danych ciągłych naturalnym wyborem dla rozkładów składowych jest wielowymiarowy Gaussian, który daje tak zwaną mieszankę rozkładów z rodziny Gaussów. Parametry mieszaniny Gaussów to w_i=P(C=i) (waga każdego składnika), μ_i (średnia każdego składnika) i Σ_i (kowariancja każdego składnika). Rysunek  (a) przedstawia mieszaninę trzech Gaussów; ta mieszanina jest w rzeczywistości źródłem danych w (b), a także modelem pokazanym na rysunku  (a). ) z surowych danych, takich jak na rysunku (b). Oczywiście, gdybyśmy wiedzieli, który komponent wygenerował każdy punkt danych, łatwo byłoby odzyskać komponent Gaussians. Z drugiej strony, gdybyśmy znali parametry każdego komponentu, moglibyśmy, przynajmniej w sensie probabilistycznym, przypisać każdy punkt danych do komponentu. Problem w tym, że nie znamy ani przypisania, ani parametrów. Podstawową ideą EM w tym kontekście jest udawanie, że znamy parametry modelu, a następnie wnioskowanie prawdopodobieństwa, że ​​każdy punkt danych należy do każdego składnika. Następnie ponownie dopasowujemy komponenty do danych, gdzie każdy komponent jest dopasowywany do całego zbioru danych, przy czym każdy punkt jest ważony prawdopodobieństwem, że należy do tego komponentu. Proces iteruje aż do zbieżności. Zasadniczo „uzupełniamy” dane, wnioskując rozkłady prawdopodobieństwa nad ukrytymi zmiennymi – do których komponentu należy każdy punkt danych -na podstawie bieżącego modelu. W przypadku mieszanki Gaussów arbitralnie inicjujemy parametry modelu mieszanego, a następnie wykonujemy następujące dwa kroki:

1. E-etap: Oblicz prawdopodobieństwa p_ij=P(C=i|x_j), prawdopodobieństwo, że punkt odniesienia x_j został wygenerowany przez składnik i. Zgodnie z regułą Bayesa mamy p_ij= αP(x_j|C=i)P(C=i). Wyrażenie P(x_j|C=i) jest po prostu prawdopodobieństwem przy x_ji-tego gaussowskiego, a termin P(C=i) jest tylko parametrem wagi dla i-tego gaussowskiego. Zdefiniuj n_i= Σ_jp_ij, efektywną liczbę punktów danych aktualnie przypisanych do komponentu i.

2. Krok M: Oblicz nową średnią, kowariancję i wagi składników, wykonując kolejno następujące kroki:

gdzie N jest całkowitą liczbą punktów danych. E-etap lub krok oczekiwania może być postrzegany jako obliczanie wartości oczekiwanych p_ij ukrytych zmiennych wskaźnikowych Z_ij, gdzie Z_ij wynosi 1, jeśli punkt odniesienia x_j został wygenerowany przez i-ty składnik, a 0 w przeciwnym razie. Krok M lub krok maksymalizacji znajduje nowe wartości parametrów, które maksymalizują prawdopodobieństwo dziennika danych, biorąc pod uwagę oczekiwane wartości ukrytych zmiennych wskaźnika. Ostateczny model, którego EM uczy się po zastosowaniu go do danych z rysunku (a), pokazano na rysunku (c); jest praktycznie nie do odróżnienia od oryginalnego modelu, z którego dane zostały wygenerowane (linia pozioma).

Rysunek (a) przedstawia logarytm prawdopodobieństwa danych zgodnie z bieżącym modelem w miarę postępu EM. Należy zwrócić uwagę na dwa punkty. Po pierwsze, logarytm prawdopodobieństwa końcowego wyuczonego modelu nieznacznie przekracza model oryginalny, z którego zostały wygenerowane dane. Może się to wydawać zaskakujące, ale po prostu odzwierciedla fakt, że dane zostały wygenerowane losowo i może nie zapewniać dokładnego odzwierciedlenia podstawowego modelu. Drugą kwestią jest to, że EM zwiększa J prawdopodobieństwo dziennika danych w każdej iteracji. Ten fakt można ogólnie udowodnić. Co więcej, pod pewnymi warunkami (które występują w większości przypadków), można udowodnić, że EM osiąga lokalne maksimum z prawdopodobieństwem. (W rzadkich przypadkach może osiągnąć punkt siodłowy lub nawet lokalne minimum.) W tym sensie EM przypomina algorytm pokonywania wzniesień oparty na gradientach, ale zauważ, że nie ma parametru „rozmiar kroku”. Sprawy nie zawsze idą tak dobrze, jak może sugerować Rysunek (a).

Może się na przykład zdarzyć, że jeden składnik Gaussa skurczy się tak, że obejmuje tylko jeden punkt danych. Wtedy jego wariancja spadnie do zera, a prawdopodobieństwo pójdzie do nieskończoności! Jeśli nie wiemy, ile składników jest w mieszaninie, musimy wypróbować różne wartości k i zobaczyć, który jest najlepszy; które może być źródłem błędu. Innym problemem jest to, że dwa komponenty mogą się „scalać”, uzyskując identyczne średnie i wariancje oraz dzieląc się swoimi punktami danych. Tego rodzaju zdegenerowane maksima lokalne stanowią poważny problem, zwłaszcza w dużych wymiarach. Jednym z rozwiązań jest umieszczenie priorytetów na parametrach modelu i zastosowanie wersji EM MAP. Innym jest ponowne uruchomienie komponentu z nowymi losowymi parametrami, jeśli stanie się zbyt mały lub zbyt blisko innego komponentu. Rozsądna inicjalizacja również pomaga.

https://aie24.pl/

Skupiono się na badaniach klinicznych rzeczywistości wirtualnej i rzeczywistości rozszerzonej. Podzielono na trzy główne części: opis zdrowia psychicznego, VR i AR , aktualny stan zdrowia psychicznego i praktyki dobrostanu , rzeczywistość wirtualna i kliniczna rzeczywistość rozszerzona badania naukowe oraz zapotrzebowanie na miary rzeczywistości wirtualnej i rozszerzonej, miary kognitywne i wiele środków, od śledzenia wzroku po korelacje mózgowe. W części poświęconej zdrowiu psychicznemu opisano obecne praktyki psychologiczne w zakresie psychiatrii i kliniki, a następnie podkreślono ograniczenia. Omówiono nowe ramy oceny i leczenia zaburzeń psychicznych zaproponowane przez NIMH. Proponowane nowe ramy podkreślają potrzebę przesunięcia punktu ciężkości z kategorii Podręcznika diagnostyczno-statystycznego zaburzeń psychicznych (DSM) na bardziej biologiczne, poznawcze i behawioralne konstrukty, które uważa się za elementy budulcowe zaburzeń psychicznych. W tej części omówiono biopsychospołeczne perspektywy zaburzeń psychicznych, a nie kategorie DSM. W rozdziale opisano konceptualizację rzeczywistości wirtualnej i rzeczywistości rozszerzonej oraz podkreślono kluczowe elementy, które są niezbędne, aby wrażenia użytkownika były jak najbardziej realne podczas interakcji z wirtualnymi obiektami umieszczonymi w całkowicie immersyjnym środowisku wirtualnym używanym w wysoce immersyjnym wyświetlaczu VR montowanym na głowie systemy, takie jak HTCVive lub Oculus Rift, lub wirtualne obiekty umieszczone w ich obecnym świecie rzeczywistym w ramach systemów rzeczywistości rozszerzonej, takich jak HoloLens lub Magic Leap. Wysoce wciągający interfejs VR oddziela użytkownika od świata rzeczywistego i wymaga uwagi użytkownika na środowisku wirtualnym. Rzeczywistość wirtualna tworzy inkluzywne, obszerne, żywe, 360 ° wyświetlacze i pozwala użytkownikom kontrolować obiekt i przewidywać jego przyszły kierunek działania, dopasowany do egocentrycznego/allocentrycznego punktu widzenia użytkownika w danym środowisku wirtualnym. Z drugiej strony, rzeczywistość rozszerzona tworzy rozległy i żywy obiekt wirtualny oraz wykorzystuje koncepcje dopasowania i interakcji podobne do urządzeń VR, aby umożliwić użytkownikowi doświadczenie jak najbardziej rzeczywistej interakcji, będąc obecnym w rzeczywistym świecie. W rozdziale wprowadzono dwa ważne kluczowe pojęcia, iluzję poczucia obecności/miejsca oraz iluzję wiarygodności, które określają wrażenia użytkownika podczas interakcji z wirtualnym obiektem umieszczonym w środowisku wirtualnym (VR) lub środowisku rzeczywistym (AR). Po uświadomieniu sobie fundamentalnej różnicy między tymi dwoma systemami zasugerowano, że oba systemy powinny wykorzystywać różne miary do oceny doświadczenia użytkownika. Działy badań klinicznych VR i AR omawiały trendy badawcze ostatnich 20 lat. Podkreślono główne zaburzenia psychiczne, które badano przy użyciu obu technologii. Badania kliniczne VR mogą zbadać ocenę, wyjaśnienie / rozwój teorii i aspekt leczenia zaburzeń psychicznych. Terapie stosowane w badaniach klinicznych VR to przede wszystkim ekspozycja, odwracanie uwagi i trening, podczas gdy AR ograniczało się tylko do terapii ekspozycyjnej. W tych sekcjach podkreślono również ograniczenia obserwacji poczynionych w tych badaniach. Omówiliśmy ograniczenia w realizacji przyszłych ścieżek takich badań, a jednocześnie rozpoznaliśmy odejście od tradycyjnych praktyk klinicznych do bardziej zaawansowanych badań i praktyk klinicznych w przyszłości. Ostatnim wkładem tego rozdziału było sformułowanie zaleceń dla przyszłych badań klinicznych VR i AR. W rozdziale zalecono zastosowanie wielu miar do badania bardziej olistycznych biopsychospołecznych perspektyw zaburzeń psychicznych. W rozdziale zasugerowano trzy miary: miary VR/AR, korelaty biologiczne i miary poznawcze, które powinny zostać włączone do przyszłych badań klinicznych VR/AR. Korelaty biologiczne mogą różnić się od monitorowania fizjologicznego do korelatów mózgowych, gdy są obecne w systemie VR lub AR, wykorzystując elektroencefalografię lub pomiary potencjału związanego ze zdarzeniami. W przyszłości badania VR i AR powinny, jeśli to możliwe, wykorzystywać techniki fMRI do badania korelacji mózgowych uczestników przed interwencjami i po nich. Zasugerowano, że takie badania mogą również ocenić obszary sieci trybów domyślnych (DMN) w niezdrowym mózgu w porównaniu ze zdrowym mózgiem i ocenić zdolności adaptacyjne i plastyczność indywidualnego mózgu. Omówiono również potrzebę mierzenia zaangażowania poznawczego i przetwarzania poznawczego, zwłaszcza w przypadku badania pacjentów ze zdrowiem psychicznym. W rozdziale opisano kilka badań, w tym badanie z mojego własnego laboratorium, które zademonstrowało zastosowanie środków śledzenia głowy VR w celu zrozumienia zaangażowania poznawczego podczas interakcji z wirtualnym środowiskiem

---

https://aie24.pl/

Poprzednia sekcja dotyczyła w pełni obserwowalnego przypadku. Wiele rzeczywistych problemów ma ukryte zmienne (czasami nazywane zmiennymi ukrytymi), których nie można zaobserwować w danych. Na przykład dokumentacja medyczna często zawiera zaobserwowane objawy, diagnozę lekarza, zastosowane leczenie i być może wynik leczenia, ale rzadko zawiera bezpośrednią obserwację samej choroby! (Zauważ, że diagnoza nie jest chorobą; jest to przyczynowa konsekwencja zaobserwowanych objawów, które z kolei są spowodowane chorobą.) Można by zapytać: „Jeśli nie obserwuje się choroby, czy możemy skonstruować model oparty wyłącznie na obserwowane zmienne?” Odpowiedź pojawia się na rysunku, która przedstawia mały, fikcyjny model diagnostyczny chorób serca. Istnieją trzy obserwowalne czynniki predysponujące i trzy obserwowalne objawy (które są zbyt przygnębiające, by je wymienić). Załóżmy, że każda zmienna ma trzy możliwe wartości (np. brak, umiarkowana i poważna). Usunięcie ukrytej zmiennej z sieci w (a) daje sieć w (b); całkowita liczba parametrów wzrasta z 78 do 708. Tak więc zmienne latentne mogą radykalnie zmniejszyć liczbę parametrów wymaganych do określenia sieci bayesowskiej. To z kolei może radykalnie zmniejszyć ilość potrzebnych danych aby nauczyć się parametrów. Ukryte zmienne są ważne, ale komplikują problem uczenia się. Na przykład na rysunku (a) nie jest oczywiste, jak nauczyć się rozkładu warunkowego HeartDisease, biorąc pod uwagę jego rodziców, ponieważ nie znamy wartości HeartDisease w każdym przypadku; ten sam problem pojawia się przy poznawaniu rozkładów objawów. Ta sekcja opisuje algorytm zwany oczekiwaniem – maksymalizacją lub EM, który rozwiązuje ten problem w bardzo ogólny sposób. Pokażemy trzy przykłady, a następnie przedstawimy ogólny opis. Algorytm na pierwszy rzut oka wydaje się magią, ale kiedy intuicja zostanie rozwinięta, można znaleźć zastosowanie EM w wielu różnych problemach związanych z uczeniem się.

https://aie24.pl/

AR, w przeciwieństwie do VR, nie potrzebuje w pełni immersyjnego, dynamicznego, bogatego otoczenia 360°, ale raczej wykorzystuje rzeczywiste fizyczne przestrzenie i wprowadza obiekt/zdarzenie do realnego świata z punktu widzenia użytkownika. Badania kliniczne nad AR skupiały się głównie na leczeniu, a dokładniej na terapiach fobii małych zwierząt, takich jak karaluchy i pająki, oraz fobii wysokości, tj. akrofobii . Badania kliniczne nad AR są bardzo zróżnicowane pod względem wielkości próby i podejścia. W przeważającej części badania kliniczne nad AR wykorzystywały karaluchy jako wirtualne bodźce wbudowane w rzeczywisty świat pacjentów . Literatura różni się od opisania studium przypadku pojedynczego pacjenta, przez mniej niż 10 pacjentów , do ponad 20 zdrowych osób dorosłych lub pacjentów .Jeśli chodzi o środki, badania kliniczne nad AR wydają się podążać śladami badań klinicznych VR. Podobnie jak w badaniach klinicznych VR, w badaniach tych wykorzystano kwestionariusze i poproszono ich uczestników o samodzielne zgłaszanie lęku , obecność , ocena rzeczywistości , zachowanie unikowe , skala nasilenia klinicznego  oraz ocena oczekiwań i satysfakcji . W badaniach tych nie odnotowano żadnych AR i powiązanych mierników, które mogłyby obiektywnie informować o wycofaniu poznawczym pacjentów (np. skupianie się na bodźcu, nieoddalanie się lub odwracanie głowy od bodźca, szczególnie gdy znajduje się on w ich obecnej przestrzeni fizycznej; przypominać sobie szczegóły takiej interakcji i bodźca) i fizyczne wycofanie (np. skurcze mięśni podczas zbliżania się do bodźca strachu lub częstotliwość, z jaką mięśnie zostały napięte lub opóźnienie w zbliżaniu się do bodźca). Miary AR mogą być również wykorzystywane do oceny strategii podejścia (np. zwiększona częstotliwość dotykania zwierzęcia, modulacja skurczów mięśni, bardziej trwałe skupienie się na bodźcu, lepsze przypominanie otoczenia niż stan lęku) podczas i po interwencji AR. W przyszłości pomiary te mogą również obejmować zapis fizjologiczny, taki jak częstość akcji serca lub przewodnictwo skórne, lub zmiany w ich DMN, jak wspomniano wcześniej w odniesieniu do klinicznych badań VR.

Podobnie jak w badaniach klinicznych w VR, wprowadzanie wirtualnego elementu do rzeczywistego świata było ściśle kontrolowane i odbywało się pod nadzorem klinicysty o stopniowanej złożoności o różnej wielkości, liczbie i otaczających szczegółach . Jednak AR wyróżnia się liczbą sesji, które były wymagane do zmniejszenia lęku w odpowiedzi na bodziec fobiczny. Kliniczne badania nad AR przebiegały zgodnie z wytycznymi dotyczącymi leczenia jednosesyjnego , które intensywnie eksponują na bodziec fobiczny trwający do trzech godzin. Pojedyncza sesja AR składała się z oglądania, dotykania i wreszcie zabicia jednego lub dwóch w związku z progresją bodźców. Jak wspomniano wcześniej, terapeuta wybiera ich liczbę, wielkość i dynamikę w miarę postępów interakcji pacjenta z AR. Pacjenci zgłaszają swój dyskomfort i niepokój przed i po terapii ekspozycji na AR, których porównania prowadzą do badań klinicznych nad AR w celu oceny ich poziomu lęku i dyskomfortu w korespondencji z bodźcem fobicznym . Jak wspomniano w sekcji pomiaru VR, AR musi również skalować techniki pomiarowe, aby umożliwić obiektywne perspektywy i psychospołeczne.

https://aie24.pl/

Możliwe jest poznanie modelu prawdopodobieństwa bez żadnych założeń dotyczących jego struktury i parametryzacji poprzez przyjęcie metod nieparametrycznych. Zadanie nieparametrycznego szacowania gęstości jest zwykle wykonywane w domenach ciągłych, takich jak pokazany na rysunku (a).

Rysunek przedstawia funkcję gęstości prawdopodobieństwa na przestrzeni określonej przez dwie zmienne ciągłe. Na rysunku (b) widzimy próbkę punktów danych z tej funkcji gęstości.

Pytanie brzmi, czy możemy odzyskać model z próbek? Najpierw rozważymy modele k-najbliższych sąsiadów. (Widzieliśmy modele najbliższego sąsiedztwa do klasyfikacji i regresji; tutaj widzimy je do estymacji gęstości). Mając próbkę punktów danych, aby oszacować nieznaną gęstość prawdopodobieństwa w punkcie zapytania x, możemy po prostu zmierzyć gęstość punktów danych w sąsiedztwie x. Rysunek (b) pokazuje dwa punkty zapytania (małe kwadraty). Dla każdego punktu zapytania narysowaliśmy najmniejszy okrąg obejmujący 10 sąsiadów — 10 najbliższych sąsiadów. Widzimy, że środkowy okrąg jest duży, co oznacza, że ​​jest tam małe zagęszczenie, a okrąg po prawej jest mały, co oznacza, że ​​jest tam duże zagęszczenie. Na rysunku pokazujemy trzy wykresy szacowania gęstości przy użyciu k-nearest-neighbors, dla różnych wartości k. Wydaje się jasne, że (b) ma mniej więcej rację, podczas gdy (a) jest zbyt kolczaste (k jest za małe), a (c) jest zbyt gładkie (k jest za duże). Inną możliwością jest użycie funkcji jądra, tak jak zrobiliśmy to w przypadku regresji ważonej lokalnie.

Aby zastosować model jądra do szacowania gęstości, załóżmy, że każdy punkt danych generuje własną funkcję małej gęstości. Na przykład możemy użyć sferycznych Gaussa z odchyleniem standardowym w wzdłuż każdej osi. Następnie szacowana gęstość w punkcie zapytania x jest średnią jąder danych:

gdzie d jest liczbą wymiarów w x, a D jest funkcją odległości euklidesowej. Nadal mamy problem z doborem odpowiedniej wartości szerokości jądra w; Rysunek pokazuje wartości, które są za małe, w sam raz i za duże. Dobrą wartość w można wybrać za pomocą walidacji krzyżowej.

https://aie24.pl/

Ta sekcja skupia się na drugiej powstającej technologii, rzeczywistości rozszerzonej, jako pomocy w badaniach nad zdrowiem psychicznym i praktykach klinicznych. Omówimy najnowocześniejsze badania augmentatywne i ich ograniczenia. Powstające urządzenia AR, takie jak HoloLens i Magic Leap, stają się kolejnym narzędziem do badania problemów ze zdrowiem psychicznym i samopoczuciem. Podobnie jak VR, rozszerzona rzeczywistość pozwala użytkownikom na interakcję z bodźcami, które z różnych powodów mogą nie być możliwe lub nie pasować do rzeczywistych scenariuszy. AR można uznać za podczęść technologii wirtualnych, w której wirtualne obiekty są umieszczane w rzeczywistym świecie w czasie rzeczywistym. W ustawieniach AR użytkownik wchodzi w interakcję z wirtualnym obiektem, jednocześnie doświadczając świata rzeczywistego. W przeciwieństwie do wirtualnej rzeczywistości, w której użytkownik zostaje całkowicie przeniesiony do wirtualnego sztucznego środowiska, rozszerzona rzeczywistość nie wypiera użytkownika z jego obecnej fizycznej przestrzeni i wyświetla wirtualne sztuczne obiekty w widoku rzeczywistego świata użytkownika. Ponieważ rzeczywistość rozszerzona buduje elementy wirtualne nałożone na dotychczasową percepcję świata rzeczywistego przez użytkownika, oferuje kilka zalet w porównaniu z rzeczywistością wirtualną. Celem rozszerzenia wirtualnych obiektów na rzeczywisty świat użytkownika jest zwiększenie doświadczenia i/lub wiedzy o jego obecnym świecie. Aby jakikolwiek system można było uznać za AR, system musi mieć następujące cechy :

• System powinien scalać obiekty rzeczywiste i wirtualne w świecie rzeczywistym lub środowisku rzeczywistym.
• System powinien działać interaktywnie i synchronizować się w czasie rzeczywistym.
• System powinien rejestrować (wyrównywać) ze sobą obiekty wirtualne i rzeczywiste.

Doświadczenie użytkownika rzeczywistości rozszerzonej zasadniczo różni się od rzeczywistości wirtualnej. W przeciwieństwie do VR, AR nie umniejsza poczucia obecności ze świata rzeczywistego i nie przenosi użytkowników do krainy czarów Alicji przez lornetkowe okulary VR. AR wymaga raczej utrzymania nienaruszonego poczucia obecności użytkownika w rzeczywistym świecie, a jednocześnie sprawia, że ​​użytkownik czuje, że wirtualny obiekt, z którym wchodzi w interakcję, jest częścią tego rzeczywistego świata. Oczekuje się, że wirtualny obiekt powinien odwzajemnić intencje i działania użytkownika w czasie rzeczywistym i sprawić, że użytkownik poczuje się tak, jakby wirtualny obiekt był częścią rzeczywistego świata. Iluzja, która sprawia, że ​​użytkownik sądzi, że przedstawiany scenariusz faktycznie występuje w środowisku, jest znana jako iluzja wiarygodności. Oznacza to, że AR może wymagać innych środków do oceny doświadczenia użytkownika niż doświadczenie użytkownika z VR. Biorąc pod uwagę, że to interakcja z wirtualnym obiektem, który jest prezentowany w przestrzeni świata rzeczywistego użytkownika, jest kluczową różnicą między rzeczywistością wirtualną a rzeczywistością rozszerzoną, rzeczywistość rozszerzona wymaga większej iluzji wiarygodności niż iluzji miejsca , aby umożliwić użytkownikowi naśladowanie rzeczywista reakcja, tak jak w czasie rzeczywistym. Złudzenie miejsca (PI) jest zdeterminowane przez sensomotoryczne zdarzenia generowane przez system rzeczywistości wirtualnej, podczas gdy, jak opisuje Slater, „złudzenie wiarygodności (PSI) jest zdeterminowane przez stopień, w jakim system może wytworzyć zdarzenia, które bezpośrednio odnoszą się do uczestnika i ogólną wiarygodność przedstawionego scenariusza w porównaniu z oczekiwaniami.” To ścisła koordynacja między rzeczywistymi i wirtualnymi obiektami oraz ich interakcja z użytkownikiem tworzy doświadczenie w AR. Jednak realizm (stopień zbieżności między oczekiwanym doświadczeniem a rzeczywistym doświadczeniem w środowisku wirtualnym) i rzeczywistość (zakres, w jakim użytkownik doświadcza środowiska hybrydowego, takiego jak rzeczywiste) może nadal mieć znaczenie dla rzeczywistości rozszerzonej.