https://aie24.pl/
Każdy węzeł w sieci nazywany jest jednostką. Tradycyjnie, zgodnie z projektem zaproponowanym przez McCullocha i Pittsa, jednostka oblicza ważoną sumę danych wejściowych z poprzednich węzłów, a następnie stosuje funkcję nieliniową w celu uzyskania swoich danych wyjściowych. Niech aj oznacza wyjście jednostki j i niech wi,j być masą przymocowaną do ogniwa od jednostki i do jednostki j; Następnie mamy
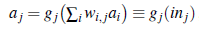
gdzie gj jest nieliniową funkcją aktywacji związaną z jednostką j, a inj jest ważoną sumą wejść do jednostki j. Podobnie określamy, że każda jednostka ma dodatkowe wejście z fikcyjnej jednostki 0, która jest ustalona na +1 i wagę w0,j dla tego wejścia. Dzięki temu całkowite ważone dane wejściowe wj do jednostki j mogą być niezerowe, nawet jeśli dane wyjściowe z poprzedniej warstwy są wszystkie zerowe. Przy tej konwencji możemy zapisać powyższe równanie w postaci wektorowej:
aj = gj(wTx)
gdzie gj jest nieliniową funkcją aktywacji związaną z jednostką j, a inj jest ważoną sumą wejść do jednostki j. Podobnie jak w rozdziale 19.6.3 (strona 697), określamy, że każda jednostka ma dodatkowe wejście z fikcyjnej jednostki 0, która jest ustalona na +1 i wagę w0,j dla tego wejścia. Dzięki temu całkowite ważone dane wejściowe wj do jednostki j mogą być niezerowe, nawet jeśli dane wyjściowe z poprzedniej warstwy są wszystkie zerowe. Przy tej konwencji możemy zapisać powyższe równanie w postaci wektorowej:
aj = gj(wTx) (22,1)
gdzie w jest wektorem wag prowadzących do jednostki j (w tym w0,j), a x jest wektorem wejść do jednostki j (w tym +1). Fakt, że funkcja aktywacji jest nieliniowa, jest ważny, ponieważ gdyby tak nie było, dowolna kompozycja jednostek nadal reprezentowałaby funkcję liniową. Nieliniowość jest tym, co pozwala wystarczająco dużym sieciom jednostek reprezentować dowolne funkcje. Uniwersalne twierdzenie o aproksymacji mówi, że sieć z zaledwie dwoma warstwami jednostek obliczeniowych, pierwszą nieliniową, a drugą liniową, może aproksymować dowolną funkcję ciągłą z dowolnym stopniem dokładności. Dowód pokazuje, że wykładniczo duża sieć może reprezentować wykładniczo wiele „wybrzuszeń” o różnych wysokościach w różnych miejscach w przestrzeni wejściowej, a tym samym przybliżać pożądaną funkcję. Innymi słowy, wystarczająco duże sieci mogą implementować tablicę przeglądową dla funkcji ciągłych, podobnie jak wystarczająco duże drzewa decyzyjne implementują tablicę przeglądową dla funkcji logicznych. Wykorzystywanych jest wiele różnych funkcji aktywacji. Najczęstsze to:
- Funkcja logistyczna lub sigmoidalna, która jest również używana w regresji logistycznej (patrz strona 703):
σ(x) = 1/(1+e-x) :
- Funkcja ReLU, której nazwa jest skrótem od wyprostowanej jednostki liniowej:
ReLU(x) = max(0,x) :
- Funkcja softplus, płynna wersja funkcji ReLU:
softplus(x) = log(1+ex) :
Pochodną funkcji softplus jest funkcja sigmoidalna.
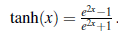
Zauważ, że zakres tanh to (-1;+1). Tanh jest przeskalowaną i przesuniętą wersją sigmoidy, ponieważ tanh(x)=2σ(2x)-1. Funkcje te pokazano na rysunku.
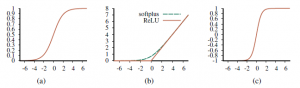
Zauważ, że wszystkie z nich są monotonicznie niemalejące, co oznacza, że ich pochodne g0 są nieujemne. Więcej o wyborze funkcji aktywacji powiemy w dalszej części. Połączenie wielu jednostek razem w sieć tworzy złożoną funkcję, która jest złożeniem wyrażeń algebraicznych reprezentowanych przez poszczególne jednostki. Na przykład sieć pokazana na rysunku (a)
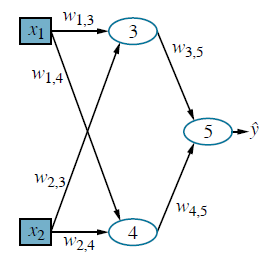
reprezentuje funkcję hw(x), sparametryzowaną wagami w, która odwzorowuje dwuelementowy wektor wejściowy x na skalarną wartość wyjściową 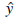 . Wewnętrzna struktura funkcji odzwierciedla strukturę sieci. Na przykład możemy napisać wyrażenie na wyjście
. Wewnętrzna struktura funkcji odzwierciedla strukturę sieci. Na przykład możemy napisać wyrażenie na wyjście 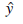 w następujący sposób:
w następujący sposób:
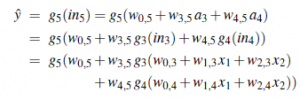
Zatem mamy wyjście 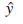
wyrażone jako funkcja hw(x) wejść i wag.
Rysunek (a) pokazuje tradycyjny sposób przedstawiania sieci w książce o sieciach neuronowych. Bardziej ogólnym sposobem myślenia o sieci jest graf obliczeniowy lub graf przepływu danych – zasadniczo obwód, w którym każdy węzeł reprezentuje podstawowe obliczenia. Rysunek (b) przedstawia wykres obliczeń odpowiadający sieci z rysunku (a);
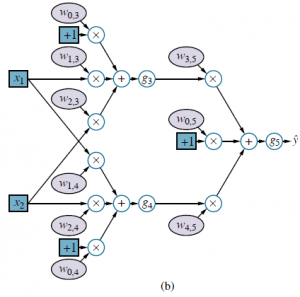
wykres uwydatnia każdy element całościowego obliczenia. Rozróżnia również dane wejściowe (na niebiesko) i wagi (jasnofioletowe): wagi można dostosować, aby dane wyjściowe 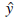 były bardziej zgodne z rzeczywistą wartością y w danych treningowych. Każda waga jest jak pokrętło regulacji głośności, które określa, ile następny węzeł na wykresie słyszy od tego konkretnego poprzednika na wykresie. Tak jak równanie opisuje działanie jednostki w postaci wektorowej, możemy zrobić coś podobnego dla sieci jako całości. Do oznaczenia macierzy wag będziemy na ogół używać W; dla tej sieci, W(1) oznacza wagi w pierwszej warstwie (w1,3, w1,4 itd.), a W(2) oznacza wagi w drugiej warstwie (w3,5 itd.). Wreszcie, niech g(1) i g(2) oznaczają funkcje aktywacji w pierwszej i drugiej warstwie. Wtedy całą sieć można zapisać w następujący sposób:
były bardziej zgodne z rzeczywistą wartością y w danych treningowych. Każda waga jest jak pokrętło regulacji głośności, które określa, ile następny węzeł na wykresie słyszy od tego konkretnego poprzednika na wykresie. Tak jak równanie opisuje działanie jednostki w postaci wektorowej, możemy zrobić coś podobnego dla sieci jako całości. Do oznaczenia macierzy wag będziemy na ogół używać W; dla tej sieci, W(1) oznacza wagi w pierwszej warstwie (w1,3, w1,4 itd.), a W(2) oznacza wagi w drugiej warstwie (w3,5 itd.). Wreszcie, niech g(1) i g(2) oznaczają funkcje aktywacji w pierwszej i drugiej warstwie. Wtedy całą sieć można zapisać w następujący sposób:
hw(x) = g(2)(W(2)g(1)(W(1)x))
Podobnie jak w równaniu wcześniej, wyrażenie to odpowiada wykresowi obliczeniowemu, chociaż jest znacznie prostsze niż wykres na rysunku (b): tutaj wykres jest po prostu łańcuchem z macierzami wag wprowadzanymi do każdej warstwy. Wykres na rysunku (b) jest również w pełni połączony, co oznacza, że każdy węzeł w każdej warstwie jest połączony z każdym węzłem w następnej warstwie. Jest to w pewnym sensie domyślne, ale zobaczymy, że wybór łączności sieciowej jest również ważny dla osiągnięcia efektywnego uczenia się.