Po stronie wyjściowej sieci problem kodowania nieprzetworzonych wartości danych do wartości rzeczywistych y dla węzłów wyjściowych grafu jest podobny do problemu kodowania danych wejściowych. Na przykład, jeśli sieć próbuje przewidzieć zmienną Weather , która ma wartości {słońce; deszcz; chmura; śnieg}, użylibyśmy kodowania one-hot z czterema bitami. Tyle o wartościach danych y. A co z przewidywaniem ![]()
dealnie, dokładnie odpowiadałoby to pożądanej wartości y, a strata byłaby zerowa i skończylibyśmy. W praktyce to rzadko się to zdarza – zwłaszcza zanim zaczęliśmy proces dostosowywania ciężarów! Dlatego musimy zastanowić się, co oznacza nieprawidłowa wartość wyjściowa i jak zmierzyć stratę. Wyprowadzając gradienty w równaniach, rozpoczęliśmy od funkcji straty błędu kwadratowego. Dzięki temu algebra jest prosta, ale nie jest to jedyna możliwość. W rzeczywistości w przypadku większości aplikacji głębokiego uczenia bardziej powszechne jest interpretowanie wartości wyjściowych „y jako” prawdopodobieństwa i użyć ujemnego logarytmu prawdopodobieństwa jako funkcji straty – dokładnie tak, jak zrobiliśmy to z uczeniem o maksymalnej wiarygodności . Uczenie o maksymalnej wiarygodności znajduje wartość w, która maksymalizuje prawdopodobieństwo obserwowanych danych. A ponieważ funkcja logarytmiczna jest monotoniczna, jest to równoważne maksymalizacji prawdopodobieństwa logarytmicznego danych, co z kolei jest równoważne minimalizacji funkcji straty zdefiniowanej jako logarytm prawdopodobieństwa ujemnego. (Przypomnij sobie , że rejestrowanie logów zamienia iloczyny prawdopodobieństw na sumy, które są bardziej podatne na obliczanie pochodnych). Innymi słowy, szukasz w, które minimalizuje sumę prawdopodobieństw logarytmu ujemnego N przykładów:
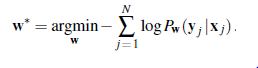
W literaturze dotyczącej głębokiego uczenia często mówi się o minimalizowaniu straty w entropii krzyżowej. Entropia krzyżowa, zapisana jako H(P;Q), jest rodzajem miary niepodobieństwa między dwoma rozkładami P i Q2 Ogólna definicja to
![]()
Z założenia funkcja softmax wyprowadza wektor liczb nieujemnych, które sumują się do 1. Jak zwykle, atrament wejściowy do każdego z węzłów wyjściowych będzie ważoną kombinacją liniową wyników z poprzedniej warstwy. Ze względu na wykładniki warstwa softmax akcentuje różnice w wejściach: na przykład, jeśli wektor wejść jest podany przez in=<5,2,0,-2>, to wyjścia mają postać <0.946,;0.047,0. 006,0.001>. Softmax jest jednak płynny i różniczkowalny , w przeciwieństwie do funkcji max. Łatwo wykazać , że esica jest softmaxem z d=2. Innymi słowy, tak jak jednostki sigmoidalne propagują informacje o klasach binarnych przez sieć, jednostki softmax propagują informacje wieloklasowe. W przypadku problemu regresji, w którym wartość docelowa y jest ciągła, często używa się liniowej warstwy wyjściowej – innymi słowy, ![]()
bez żadnej funkcji aktywacji g – i interpretuje to jako średnią prognozy Gaussa ze stałą zmienność. Jak zauważyliśmy na stronie 780, maksymalizacja wiarygodności (tj. minimalizacja prawdopodobieństwa ujemnego logarytmu) za pomocą gaussowskiego o stałej wariancji jest tym samym, co minimalizacja błędu kwadratowego. Tak więc zinterpretowana liniowa warstwa wyjściowa wykonuje klasyczną regresję liniową. Cechami wejściowymi tej regresji liniowej są dane wyjściowe z poprzedniej warstwy, które zazwyczaj wynikają z wielu nieliniowych przekształceń oryginalnych danych wejściowych do sieci. Dostępnych jest wiele innych warstw wyjściowych. Na przykład warstwa gęstości mieszaniny reprezentuje dane wyjściowe przy użyciu mieszaniny rozkładów Gaussa. (Patrz rozdział 21.3.1, aby uzyskać więcej szczegółów na temat mieszanin Gaussa). Takie warstwy przewidują względną częstotliwość każdego składnika mieszaniny, średnią każdego składnika i wariancję każdego składnika. Dopóki te wartości wyjściowe są odpowiednio interpretowane przez funkcję straty jako określającą prawdopodobieństwo dla prawdziwej wartości wyjściowej y, sieć po nauczeniu dopasuje model mieszaniny gaussowskiej w przestrzeni cech określonych przez poprzednie warstwy.