Wcześniej wprowadziliśmy podejście do nadzorowanego uczenia się oparte na gradiencie: oblicz gradient funkcji straty w odniesieniu do wag i dostosuj wagi wzdłuż kierunku gradientu, aby zmniejszyć stratę. (Jeśli nie przeczytałeś jeszcze sekcji 19.6, zdecydowanie zalecamy, abyś to zrobił przed kontynuowaniem). Możemy zastosować dokładnie to samo podejście do uczenia się wag na wykresach obliczeniowych. W przypadku wag prowadzących do jednostek w warstwie wyjściowej – tych, które dają wynik sieciowy, obliczanie gradientu jest zasadniczo identyczne z procesem opisanym w rozdziale 19.6. W przypadku wag prowadzących do jednostek w warstwach ukrytych, które nie są bezpośrednio połączone z wyjściami, proces jest tylko nieco bardziej skomplikowany. Na razie użyjemy kwadratowej funkcji straty L2 i obliczymy gradient sieci na rysunku wcześniejszym w odniesieniu do pojedynczego przykładu uczącego (x,y). (Dla wielu przykładów gradient jest po prostu sumą gradientów dla poszczególnych przykładów.) Sieć generuje przewidywanie 
a prawdziwą wartością jest y, więc mamy
Aby obliczyć gradient straty względem wag, potrzebujemy narzędzi rachunku różniczkowego, – głównie reguła łańcucha 
Zaczniemy od prostego przypadku: ciężarka takiego jak w3,5, który jest podłączony do jednostki wyjściowej. Działamy bezpośrednio na wyrażeniach definiujących sieć z równania
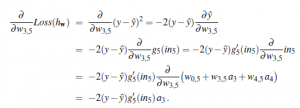
Uproszczenie w ostatnim wierszu jest następujące, ponieważ w0,5 i w4,5 a4 nie zależą od w3,5, podobnie jak współczynnik w3,5, a3. Nieco trudniejszy przypadek dotyczy ciężarka takiego jak w1,3, który nie jest bezpośrednio podłączony do jednostki wyjściowej. Tutaj musimy jeszcze raz zastosować zasadę łańcucha. Kilka pierwszych kroków są identyczne, więc pomijamy je:
Mamy więc dość proste wyrażenia na gradient straty względem wag w3,5 i w1,3. Jeśli zdefiniujemy 
jako rodzaj „postrzeganego błędu” w punkcie, w którym jednostka 5 otrzymuje swoje dane wejściowe, to gradient względem w3,5 jest po prostu Δ5a3. To ma sens: jeśli Δ5 jest dodatnie, oznacza to, że 
jest za duże (przypomnij sobie, że g0 jest zawsze nieujemne); jeśli a3 jest również dodatnie, to zwiększenie w3,5 tylko pogorszy sytuację, natomiast jeśli a3 jest ujemne, to zwiększenie w3,5 zmniejszy błąd. Znaczenie a3 również ma znaczenie: jeśli a3 jest małe w tym przykładzie treningu, to w3,5 nie odegrało większej roli w generowaniu błędu i nie trzeba go zbyt wiele zmieniać. Jeśli zdefiniujemy również 
to gradient dla w1,3 staje się po prostu Δ3x1. Tak więc postrzegany błąd na wejściu do jednostki 3 jest postrzeganym błędem na wejściu do jednostki 5, pomnożonym przez informacje na ścieżce od 5 z powrotem do 3. Zjawisko to jest całkowicie ogólne i daje początek terminowi backropagation dla sposób, w jaki błąd na wyjściu jest przekazywany z powrotem przez sieć. Inną ważną cechą tych wyrażeń gradientowych jest to, że mają one jako czynniki lokalne pochodne g’j(wj). Jak wspomniano wcześniej, te pochodne są zawsze nieujemne, ale mogą być bardzo bliskie zeru (w przypadku funkcji sigmoid, softplus i tanh) lub dokładnie zero (w przypadku ReLU), jeśli dane wejściowe z przykładu uczącego chodzi o umieszczenie jednostki j w płaskim obszarze roboczym. Jeśli pochodna g’j jest mała lub zerowa, oznacza to, że zmiana wag prowadzących do jednostki j będzie miała znikomy wpływ na jej wyjście. W rezultacie głębokie sieci z wieloma warstwami mogą ucierpieć z powodu zanikającego gradientu – sygnały błędów są całkowicie wygaszone, gdy są propagowane z powrotem przez sieć. Pokazaliśmy, że gradienty w naszej małej przykładowej sieci są prostymi wyrażeniami, które można obliczyć, przekazując przez sieć informacje z powrotem z jednostek wyjściowych. Okazuje się, że ta właściwość obowiązuje bardziej ogólnie. W rzeczywistości, , obliczenia gradientu dla dowolnego grafu obliczeń z wyprzedzeniem mają taką samą strukturę jak bazowy graf obliczeń. Własność ta wynika wprost z zasad różniczkowania. Pokazaliśmy krwawe szczegóły obliczenia gradientu, ale nie martw się: nie ma potrzeby ponownego wyprowadzania w równaniach dla każdej nowej struktury sieci! Wszystkie takie gradienty można obliczyć metodą automatycznego różniczkowania, która stosuje reguły rachunku różniczkowego w sposób systematyczny do obliczania gradientów dla dowolnego programu numerycznego. W rzeczywistości metoda wstecznej propagacji w uczeniu głębokim jest po prostu zastosowaniem zróżnicowanie trybów, które stosuje zasadę łańcucha „od zewnątrz do wewnątrz” i zyskuje korzyści wynikające z wydajności programowania dynamicznego, gdy dana sieć ma wiele wejść i stosunkowo mało wyjść. Wszystkie główne pakiety do uczenia głębokiego zapewniają automatyczne różnicowanie, dzięki czemu użytkownicy mogą swobodnie eksperymentować z różnymi strukturami sieci, funkcjami aktywacji, funkcjami utraty i formami kompozycji bez konieczności wykonywania wielu obliczeń w celu uzyskania nowego algorytmu uczenia się dla każdego eksperymentu. Zachęciło to do podejścia zwanego uczeniem od końca do końca, w którym złożony system obliczeniowy do zadania takiego jak tłumaczenie maszynowe może składać się z kilku możliwych do trenowania podsystemów; cały system jest następnie szkolony w sposób kompleksowy z par wejścia/wyjścia. Dzięki takiemu podejściu projektant musi mieć jedynie mgliste pojęcie o tym, jak powinien być zbudowany cały system; nie trzeba z góry wiedzieć, co dokładnie powinien zrobić każdy podsystem ani jak oznaczyć jego wejścia i wyjścia.