Nasze ostateczne zastosowanie EM obejmuje poznanie prawdopodobieństw przejścia w ukrytych modelach Markowa (HMM). Przypomnijmy , że ukryty model Markowa może być reprezentowany przez dynamiczną sieć Bayesa z pojedynczą dyskretną zmienną stanu, jak pokazano na rysunku
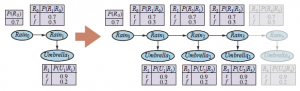
Każdy punkt danych składa się z sekwencji obserwacji o skończonej długości, więc problemem jest poznanie prawdopodobieństw przejścia ze zbioru sekwencji obserwacji (lub tylko jednej długiej sekwencji). Widzieliśmy już, jak uczyć się sieci Bayesa, ale jest to komplikacja: w sieciach Bayesa każdy parametr jest inny; z drugiej strony w ukrytym modelu Markowa poszczególne prawdopodobieństwa przejścia ze stanu i do stanu j w czasie t, θijt =P(Xt+1= j|Xt =i), są powtarzane w czasie, czyli θijt = θij dla wszystkich t. Aby oszacować prawdopodobieństwo przejścia ze stanu i do stanu j, po prostu obliczamy oczekiwany odsetek przypadków przejścia systemu do stanu j w stanie i:
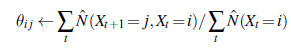
Oczekiwane liczby są obliczane przez algorytm anHMMinference. Algorytm naprzód-wstecz przedstawiony można bardzo łatwo zmodyfikować, aby obliczyć niezbędne prawdopodobieństwa. Ważną kwestią jest to, że wymagane prawdopodobieństwa uzyskuje się poprzez wygładzanie, a nie filtrowanie. Filtrowanie daje rozkład prawdopodobieństwa aktualnego stanu, biorąc pod uwagę przeszłość, ale wygładzanie daje rozkład podany wszelkimi dowodami, łącznie z tym, co dzieje się po wystąpieniu określonego przejścia. Dowody w sprawie o morderstwo są zwykle uzyskiwane po dokonaniu przestępstwa (tj. przejściu ze stanu i do stanu j).