Nienadzorowane grupowanie to problem rozróżniania wielu kategorii w kolekcji obiektów. Problem nie jest nadzorowany, ponieważ nie podano etykiet kategorii. Załóżmy na przykład, że rejestrujemy widma stu tysięcy gwiazd; czy istnieją różne typy gwiazd ujawniane przez widma, a jeśli tak, to ile typów i jakie są ich cechy charakterystyczne? Wszyscy znamy terminy takie jak „czerwony olbrzym” i „biały karzeł”, ale gwiazdy nie noszą tych etykiet na kapeluszach – astronomowie musieli wykonywać nienadzorowane grupowanie, aby zidentyfikować te kategorie. Inne przykłady obejmują identyfikację gatunków, rodzajów, rzędów, gromady itd. w taksonomii Linneusza oraz tworzenie naturalnych rodzajów dla zwykłych przedmiotów. Nienadzorowane klastrowanie zaczyna się od danych. Rysunek 21.12(b) przedstawia 500 punktów danych, z których każdy określa wartości dwóch ciągłych atrybutów. Punkty danych mogą odpowiadać gwiazdom, a atrybuty mogą odpowiadać intensywnościom widmowym przy dwóch określonych częstotliwościach. Następnie musimy zrozumieć, jaki rodzaj rozkładu prawdopodobieństwa mógł wygenerować dane. Grupowanie zakłada, że dane są generowane z rozkładu mieszaniny P. Taki rozkład ma k składników, z których każdy jest rozkładem sam w sobie. Punkt danych jest generowany przez wybranie najpierw składnika, a następnie wygenerowanie próbki z tego składnika. Niech zmienna losowa C oznacza składnik o wartościach 1,…,k; wtedy rozkład mieszaniny jest podany przez
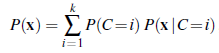
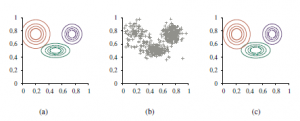
gdzie x odnosi się do wartości atrybutów dla punktu danych. W przypadku danych ciągłych naturalnym wyborem dla rozkładów składowych jest wielowymiarowy Gaussian, który daje tak zwaną mieszankę rozkładów z rodziny Gaussów. Parametry mieszaniny Gaussów to wi=P(C=i) (waga każdego składnika), μi (średnia każdego składnika) i Σi (kowariancja każdego składnika). Rysunek (a) przedstawia mieszaninę trzech Gaussów; ta mieszanina jest w rzeczywistości źródłem danych w (b), a także modelem pokazanym na rysunku (a). ) z surowych danych, takich jak na rysunku (b). Oczywiście, gdybyśmy wiedzieli, który komponent wygenerował każdy punkt danych, łatwo byłoby odzyskać komponent Gaussians. Z drugiej strony, gdybyśmy znali parametry każdego komponentu, moglibyśmy, przynajmniej w sensie probabilistycznym, przypisać każdy punkt danych do komponentu. Problem w tym, że nie znamy ani przypisania, ani parametrów. Podstawową ideą EM w tym kontekście jest udawanie, że znamy parametry modelu, a następnie wnioskowanie prawdopodobieństwa, że każdy punkt danych należy do każdego składnika. Następnie ponownie dopasowujemy komponenty do danych, gdzie każdy komponent jest dopasowywany do całego zbioru danych, przy czym każdy punkt jest ważony prawdopodobieństwem, że należy do tego komponentu. Proces iteruje aż do zbieżności. Zasadniczo „uzupełniamy” dane, wnioskując rozkłady prawdopodobieństwa nad ukrytymi zmiennymi – do których komponentu należy każdy punkt danych -na podstawie bieżącego modelu. W przypadku mieszanki Gaussów arbitralnie inicjujemy parametry modelu mieszanego, a następnie wykonujemy następujące dwa kroki:
- E-etap: Oblicz prawdopodobieństwa pij=P(C=i|xj), prawdopodobieństwo, że punkt odniesienia xj został wygenerowany przez składnik i. Zgodnie z regułą Bayesa mamy pij= αP(xj|C=i)P(C=i). Wyrażenie P(xj|C=i) jest po prostu prawdopodobieństwem przy xji-tego gaussowskiego, a termin P(C=i) jest tylko parametrem wagi dla i-tego gaussowskiego. Zdefiniuj ni= Σjpij, efektywną liczbę punktów danych aktualnie przypisanych do komponentu i.
2. Krok M: Oblicz nową średnią, kowariancję i wagi składników, wykonując kolejno następujące kroki:
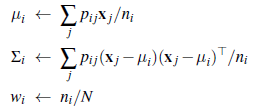
gdzie N jest całkowitą liczbą punktów danych. E-etap lub krok oczekiwania może być postrzegany jako obliczanie wartości oczekiwanych pij ukrytych zmiennych wskaźnikowych Zij, gdzie Zij wynosi 1, jeśli punkt odniesienia xj został wygenerowany przez i-ty składnik, a 0 w przeciwnym razie. Krok M lub krok maksymalizacji znajduje nowe wartości parametrów, które maksymalizują prawdopodobieństwo dziennika danych, biorąc pod uwagę oczekiwane wartości ukrytych zmiennych wskaźnika. Ostateczny model, którego EM uczy się po zastosowaniu go do danych z rysunku (a), pokazano na rysunku (c); jest praktycznie nie do odróżnienia od oryginalnego modelu, z którego dane zostały wygenerowane (linia pozioma).
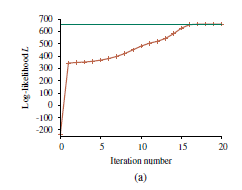
Rysunek (a) przedstawia logarytm prawdopodobieństwa danych zgodnie z bieżącym modelem w miarę postępu EM. Należy zwrócić uwagę na dwa punkty. Po pierwsze, logarytm prawdopodobieństwa końcowego wyuczonego modelu nieznacznie przekracza model oryginalny, z którego zostały wygenerowane dane. Może się to wydawać zaskakujące, ale po prostu odzwierciedla fakt, że dane zostały wygenerowane losowo i może nie zapewniać dokładnego odzwierciedlenia podstawowego modelu. Drugą kwestią jest to, że EM zwiększa J prawdopodobieństwo dziennika danych w każdej iteracji. Ten fakt można ogólnie udowodnić. Co więcej, pod pewnymi warunkami (które występują w większości przypadków), można udowodnić, że EM osiąga lokalne maksimum z prawdopodobieństwem. (W rzadkich przypadkach może osiągnąć punkt siodłowy lub nawet lokalne minimum.) W tym sensie EM przypomina algorytm pokonywania wzniesień oparty na gradientach, ale zauważ, że nie ma parametru „rozmiar kroku”. Sprawy nie zawsze idą tak dobrze, jak może sugerować Rysunek (a).
Może się na przykład zdarzyć, że jeden składnik Gaussa skurczy się tak, że obejmuje tylko jeden punkt danych. Wtedy jego wariancja spadnie do zera, a prawdopodobieństwo pójdzie do nieskończoności! Jeśli nie wiemy, ile składników jest w mieszaninie, musimy wypróbować różne wartości k i zobaczyć, który jest najlepszy; które może być źródłem błędu. Innym problemem jest to, że dwa komponenty mogą się „scalać”, uzyskując identyczne średnie i wariancje oraz dzieląc się swoimi punktami danych. Tego rodzaju zdegenerowane maksima lokalne stanowią poważny problem, zwłaszcza w dużych wymiarach. Jednym z rozwiązań jest umieszczenie priorytetów na parametrach modelu i zastosowanie wersji EM MAP. Innym jest ponowne uruchomienie komponentu z nowymi losowymi parametrami, jeśli stanie się zbyt mały lub zbyt blisko innego komponentu. Rozsądna inicjalizacja również pomaga.