Możliwe jest poznanie modelu prawdopodobieństwa bez żadnych założeń dotyczących jego struktury i parametryzacji poprzez przyjęcie metod nieparametrycznych. Zadanie nieparametrycznego szacowania gęstości jest zwykle wykonywane w domenach ciągłych, takich jak pokazany na rysunku (a).
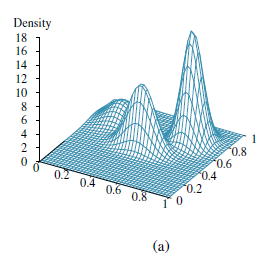
Rysunek przedstawia funkcję gęstości prawdopodobieństwa na przestrzeni określonej przez dwie zmienne ciągłe. Na rysunku (b) widzimy próbkę punktów danych z tej funkcji gęstości.
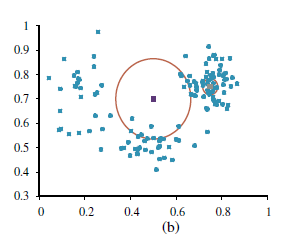
Pytanie brzmi, czy możemy odzyskać model z próbek? Najpierw rozważymy modele k-najbliższych sąsiadów. (Widzieliśmy modele najbliższego sąsiedztwa do klasyfikacji i regresji; tutaj widzimy je do estymacji gęstości). Mając próbkę punktów danych, aby oszacować nieznaną gęstość prawdopodobieństwa w punkcie zapytania x, możemy po prostu zmierzyć gęstość punktów danych w sąsiedztwie x. Rysunek (b) pokazuje dwa punkty zapytania (małe kwadraty). Dla każdego punktu zapytania narysowaliśmy najmniejszy okrąg obejmujący 10 sąsiadów — 10 najbliższych sąsiadów. Widzimy, że środkowy okrąg jest duży, co oznacza, że jest tam małe zagęszczenie, a okrąg po prawej jest mały, co oznacza, że jest tam duże zagęszczenie. Na rysunku pokazujemy trzy wykresy szacowania gęstości przy użyciu k-nearest-neighbors, dla różnych wartości k. Wydaje się jasne, że (b) ma mniej więcej rację, podczas gdy (a) jest zbyt kolczaste (k jest za małe), a (c) jest zbyt gładkie (k jest za duże). Inną możliwością jest użycie funkcji jądra, tak jak zrobiliśmy to w przypadku regresji ważonej lokalnie.

Aby zastosować model jądra do szacowania gęstości, załóżmy, że każdy punkt danych generuje własną funkcję małej gęstości. Na przykład możemy użyć sferycznych Gaussa z odchyleniem standardowym w wzdłuż każdej osi. Następnie szacowana gęstość w punkcie zapytania x jest średnią jąder danych:
![]()
gdzie d jest liczbą wymiarów w x, a D jest funkcją odległości euklidesowej. Nadal mamy problem z doborem odpowiedniej wartości szerokości jądra w; Rysunek pokazuje wartości, które są za małe, w sam raz i za duże. Dobrą wartość w można wybrać za pomocą walidacji krzyżowej.
