Załóżmy, że kupujemy torebkę cukierków z limonki i wiśni od nowego producenta, którego proporcje smakowe są zupełnie nieznane; ułamek wiśni może wynosić od 0 do 1. W takim przypadku mamy kontinuum hipotez. Parametrem w tym przypadku, który nazywamy Θ , jest proporcja cukierków wiśniowych, a hipotezą jest hΘ . (Proporcja cukierków z limonką wynosi tylko 1 – Θ.) Jeśli założymy, że wszystkie proporcje są a priori jednakowo prawdopodobne, wówczas podejście maksymalnego prawdopodobieństwa jest rozsądne. Jeśli modelujemy sytuację za pomocą sieci bayesowskiej, potrzebujemy tylko jednej zmiennej losowej, Flavour (smak losowo wybranego cukierka z torebki). Ma wartości wiśnia i limonka, gdzie prawdopodobieństwo pojawienia się wiśni wynosi Θ (patrz Rysunek 21.2(a)). Załóżmy teraz, że odpakujemy N cukierków, z których c to wiśnia, l`=N – c to limonka. Zgodnie z równaniem (21.3) prawdopodobieństwo tego konkretnego zbioru danych wynosi
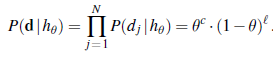
Hipoteza maksymalnego prawdopodobieństwa jest podana przez wartość Θ, która maksymalizuje to wyrażenie. Ponieważ funkcja logarytmiczna jest monotoniczna, tę samą wartość uzyskuje się poprzez maksymalizację prawdopodobieństwa logarytmicznego:
![]()
(Biorąc logarytmy, redukujemy iloczyn do sumy danych, co zwykle łatwiej jest zmaksymalizować.) Aby znaleźć wartość maksymalnego prawdopodobieństwa Θ , różnicujemy L względem Θ i ustawiamy wynikowe wyrażenie na zero:
![]()
Zatem w języku angielskim hipoteza maksymalnego prawdopodobieństwa hML zakłada, że rzeczywista proporcja cukierków wiśniowych w torebce jest równa obserwowanej proporcji w dotychczas nieopakowanych cukierkach! Wygląda na to, że wykonaliśmy dużo pracy, aby odkryć oczywistość. W rzeczywistości jednak opracowaliśmy jedną standardową metodę uczenia się parametrów maksymalnego prawdopodobieństwa, metodę o szerokim zastosowaniu:
- Napisz wyrażenie określające prawdopodobieństwo danych jako funkcję parametru(ów).
- Zapisz pochodną logarytmu wiarygodności dla każdego parametru.
- Znajdź wartości parametrów takie, że pochodne są zerowe.
Najtrudniejszym krokiem jest zwykle ostatni. W naszym przykładzie było to trywialne, ale zobaczymy, że w wielu przypadkach musimy uciec się do algorytmów rozwiązań iteracyjnych lub innych technik optymalizacji numerycznej, jak opisano w rozdziale 4.2. (Będziemy musieli zweryfikować, czy macierz Hessów jest ujemnie określona.) Przykład ilustruje również istotny problem z ogólnie uczeniem się z maksymalnym prawdopodobieństwem: gdy zbiór danych jest na tyle mały, że niektóre zdarzenia jeszcze nie zostały zaobserwowane – na przykład brak cukierki wiśniowe – hipoteza maksymalnego prawdopodobieństwa przypisuje tym zdarzeniom zerowe prawdopodobieństwo. Aby uniknąć tego problemu, stosuje się różne sztuczki, takie jak inicjowanie liczników dla każdego zdarzenia na 1 zamiast 0. Spójrzmy na inny przykład. Załóżmy, że ten nowy producent cukierków chce dać konsumentowi małą wskazówkę i używa opakowań do cukierków w kolorze czerwonym i zielonym. Opakowanie dla każdego cukierka jest wybierane probabilistycznie, zgodnie z pewnym nieznanym rozkładem warunkowym, w zależności od smaku. Odpowiedni model prawdopodobieństwa pokazano na rysunku 21.2(b). Zauważ, że ma trzy parametry: Θ, Θ1 i Θ2. Dzięki tym parametrom prawdopodobieństwo zobaczenia, powiedzmy, cukierka wiśniowego w zielonym opakowaniu można uzyskać ze standardowej semantyki dla sieci bayesowskich
![]()
Teraz odwijamy N cukierków, z których c to wiśnia, a l to limonka. Liczba opakowań jest następująca: rc cukierków wiśniowych ma czerwone opakowania, a gc zielone, natomiast rl cukierków limonkowych ma czerwone, a gl zielone. Prawdopodobieństwo danych jest podane przez
![]()
Wygląda to okropnie, ale logarytmowanie pomaga:
![]()
Korzyść z rejestrowania logów jest oczywista: prawdopodobieństwo logarytmu jest sumą trzech terminów, z których każdy zawiera jeden parametr. Kiedy weźmiemy pochodne względem każdego parametru i ustawimy je na zero, otrzymamy trzy niezależne równania, z których każde zawiera tylko jeden parametr:
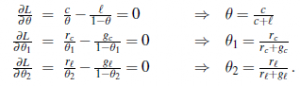
Rozwiązanie dla Θ jest takie samo jak poprzednio. Rozwiązaniem dla 1, prawdopodobieństwa, że cukierek wiśniowy ma czerwone opakowanie, jest obserwowana frakcja cukierków wiśniowych z czerwonym opakowaniem, podobnie dla 2. Wyniki te są bardzo pocieszające i łatwo zauważyć, że można je rozszerzyć na dowolną sieć bayesowską, której prawdopodobieństwa warunkowe są reprezentowane w postaci tabel. Najważniejszą kwestią jest to, że przy kompletnych danych problem uczenia się parametrów maksymalnego prawdopodobieństwa dla sieci bayesowskiej rozkłada się na oddzielne problemy uczenia się, po jednym dla każdego parametru. Drugą kwestią jest to, że wartości parametrów dla zmiennej, biorąc pod uwagę jej rodziców, są po prostu obserwowanymi częstotliwościami wartości zmiennych dla każdego ustawienia wartości rodzicielskich. Tak jak poprzednio, musimy uważać, aby uniknąć zer, gdy zestaw danych jest mały.