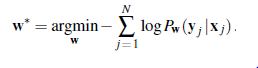W tych warunkach wzrasta prawdopodobieństwo wystąpienia fałszywego negatywu, ponieważ obszar pierwszego planu ma obszar o jednolitym kolorze, a zmiany wewnątrz obszaru pierwszego planu są spowodowane różnymi efektami świetlnymi oraz różnymi kierunkami i prędkościami ruchu.
Warstwa puli w sieci neuronowej podsumowuje zestaw sąsiednich jednostek z poprzedniej warstwy jedną wartością. Pooling działa jak warstwa konwolucji, z rozmiarem jądra l i krokiem s, ale zastosowana operacja jest ustalona, a nie wyuczona. Zazwyczaj żadna funkcja aktywacji nie jest powiązana z warstwą puli. Istnieją dwie popularne formy łączenia:
wynikiem będzie 9, co oznacza, że gdzieś w obrazie wejściowym znajduje się ciemniejsza kropka wykrywana przez jądro. Innymi słowy, łączenie maksymalne działa jak rodzaj logicznej alternatywy, mówiąc, że dana cecha istnieje gdzieś w polu receptywnym jednostki.
Jeśli celem jest zaklasyfikowanie obrazu do jednej z c kategorii, to ostatnią warstwą sieci będzie softmax z c jednostkami wyjściowymi. Wczesne warstwy CNN mają rozmiar obrazu, więc gdzieś pomiędzy musi być znaczne zmniejszenie rozmiaru warstwy. Warstwy konwolucji i warstwy puli z krokiem większym niż 1 służą do zmniejszenia rozmiaru warstwy. Możliwe jest również zmniejszenie rozmiaru warstwy po prostu przez posiadanie w pełni połączonej warstwy z mniejszą liczbą jednostek niż poprzednia warstwa. CNN często mają jedną lub dwie takie warstwy poprzedzające ostateczną warstwę softmax.
O różnych porach dnia efekty świetlne mogą się różnić ze względu na różnice w źródłach światła, odbicia od różnych źródeł światła i blokowanie światła przez inne obiekty. Wpływa to na wygląd obiektu, co może skutkować wykryciem fałszywie dodatnim lub fałszywie ujemnym. Z tych powodów konsekwencje oświetlenia są często trudne do zniesienia . Wielu autorów, próbowało różnych podejść w takich obszarach, aby zmniejszyć wyzwania związane z wariacjami oświetlenia.
Wspomnieliśmy , że obraz nie może być traktowany jako prosty wektor wejściowych wartości pikseli, głównie dlatego, że sąsiedztwo pikseli naprawdę ma znaczenie. Gdybyśmy mieli skonstruować sieć z całkowicie połączonymi warstwami i obrazem jako danymi wejściowymi, uzyskalibyśmy ten sam wynik, niezależnie od tego, czy trenowaliśmy z niezakłóconymi obrazami, czy z obrazami, których wszystkie piksele zostały losowo permutowane. Ponadto załóżmy, że w pierwszej warstwie ukrytej, do której piksele dostarczają dane wejściowe, znajduje się n pikseli i n jednostek. Jeśli wejście i pierwsza warstwa ukryta są w pełni połączone, oznacza to n2 wag; dla typowego megapikselowego obrazu RGB to 9 bilionów wag. Tak duża przestrzeń parametrów wymagałaby odpowiednio dużej liczby obrazów uczących i ogromnego budżetu obliczeniowego do uruchomienia algorytmu uczącego. Te rozważania sugerują, że powinniśmy skonstruować pierwszą ukrytą warstwę tak, aby każda ukryta jednostka J otrzymywała dane wejściowe tylko z małego, lokalnego obszaru obrazu. To zabija dwie pieczenie na jednym ogniu. Po pierwsze, szanuje sąsiedztwo, przynajmniej lokalnie. (I zobaczymy później, że jeśli kolejne warstwy mają tę samą właściwość lokalności, to sieć będzie respektować sąsiedztwo w sensie globalnym.) Po drugie, zmniejsza liczbę wag: jeśli każdy lokalny region ma l << n pikseli, to będzie w sumie l<<n2 wag. Na razie w porządku. Brakuje nam jednak innej ważnej właściwości obrazów: z grubsza mówiąc, wszystko, co można wykryć w jednym małym, lokalnym obszarze obrazu – na przykład oko lub źdźbło trawy – wyglądałoby tak samo, gdyby pojawiło się w innym małym, lokalnym obszarze Obraz. Innymi słowy, oczekujemy, że dane obrazu będą wykazywać przybliżoną niezmienność przestrzenną, przynajmniej w małej lub średniej skali. Niekoniecznie oczekujemy, że górne połowy zdjęć będą wyglądać jak dolne połowy, więc istnieje skala, poza którą niezmienność przestrzenna nie dłużej trzyma. Lokalną niezmienność przestrzenną można osiągnąć ograniczając wagi l łączące region lokalny z jednostką w warstwie ukrytej, tak aby były takie same dla każdej jednostki ukrytej. (Oznacza to, że dla jednostek ukrytych i oraz j wagi w1,i; … ,wl,i są takie same jak w1,j…,wl, j.) Dzięki temu jednostki ukryte stają się detektorami cech, które wykryj tę samą funkcję wszędzie tam, gdzie pojawia się na obrazie. Zazwyczaj chcemy, aby pierwsza warstwa ukryta wykrywała wiele rodzajów funkcji, a nie tylko jedną; więc dla każdego lokalnego regionu obrazu możemy mieć d ukrytych jednostek zd różnymi zestawami wag. Oznacza to, że we wszystkich występują wagi dl – liczba, która jest nie tylko znacznie mniejsza niż n2, ale w rzeczywistości jest niezależna od n, rozmiaru obrazu. W ten sposób, wstrzykując pewną wcześniejszą wiedzę — mianowicie wiedzę o sąsiedztwie i niezmienności przestrzennej — możemy opracować modele, które mają znacznie mniej parametrów i mogą się uczyć znacznie szybciej. Konwolucyjna sieć neuronowa (CNN) to taka, która zawiera przestrzennie lokalne połączenia, przynajmniej we wczesnych warstwach, i ma wzorce wag, które są replikowane w jednostkach w każdej warstwie. Wzorzec wag, który jest replikowany w wielu regionach lokalnych, nazywa się jądrem, a proces nakładania jądra na piksele obrazu (lub przestrzennie zorganizowane jednostki w kolejnej warstwie) nazywa się splotem. Jądra i sploty najłatwiej zilustrować w jednym wymiarze, a nie w dwóch lub więcej, więc przyjmiemy wektor wejściowy x o rozmiarze n, odpowiadający n pikselom na obrazie jednowymiarowym, oraz jądro wektora k o rozmiarze l. (Dla uproszczenia założymy, że l jest liczbą nieparzystą.) Wszystkie idee przenoszą się bezpośrednio do przypadków wyższych wymiarów. Operację splotu zapisujemy za pomocą symbolu * , na przykład: z = x* k. Operacja jest zdefiniowana w następujący sposób:
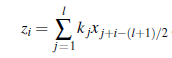
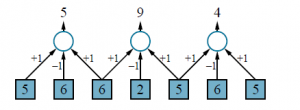
Innymi słowy, dla każdej pozycji wyjściowej i, bierzemy iloczyn skalarny między jądrem k a fragmentem x wyśrodkowanym na xi o szerokości l. Proces zilustrowano na rysunku 22.4 dla wektora jądra [+1;-1;+1], który wykrywa ciemniejszy punkt na obrazie 1D. (Wersja 2D może wykryć ciemniejszą linię.) Zauważ, że w tym przykładzie piksele, na których wyśrodkowane są jądra, są oddzielone odległością 2 pikseli; mówimy, że jądro jest stosowane z krokiem s=2. Zauważ, że warstwa wyjściowa ma mniej pikseli: z powodu kroku liczba pikseli zmniejsza się z n do mniej więcej n/s. (W dwóch wymiarach liczba pikseli wynosiłaby mniej więcej n/sxsy, gdzie sx i sy to kroki w kierunkach x i y na obrazie). Mówimy „w przybliżeniu” z powodu tego, co dzieje się na krawędzi obrazu: na rysunku splot zatrzymuje się na krawędziach obrazu, ale można również uzupełnić wejście dodatkowymi pikselami (zerami lub kopiami zewnętrznych pikseli), aby jądro mogło być zastosowane dokładnie [n/=s] razy.
W przypadku małych jąder zazwyczaj używamy s=1, więc dane wyjściowe mają takie same wymiary jak obraz . Operacja nakładania jądra na obraz może być zaimplementowana w oczywisty sposób przez program z odpowiednimi zagnieżdżonymi pętlami; ale może być również sformułowana jako pojedyncza operacja macierzowa, tak jak zastosowanie macierzy wag w równaniu . Na przykład splot przedstawiony na rysunku można postrzegać jako następujące mnożenie macierzy:
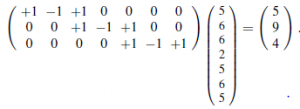
W tej macierzy wag jądro pojawia się w każdym wierszu, przesunięte zgodnie z krokiem względem poprzedniego wiersza. Niekoniecznie trzeba jawnie skonstruować macierz wag — w końcu są to głównie zera — ale fakt, że splot jest liniowy Operacja macierzowa służy jako przypomnienie, że gradient można łatwo i skutecznie zastosować do CNN, tak samo jak do zwykłych sieci neuronowych. Jak wspomniano wcześniej, będzie d jąder, a nie tylko jeden; więc przy kroku równym 1 wynik będzie d razy większy. Oznacza to, że dwuwymiarowa tablica wejściowa staje się trójwymiarową tablicą ukrytych jednostek, gdzie trzeci wymiar ma rozmiar d. Ważne jest zorganizowanie warstwy ukrytej w ten sposób, aby wszystkie dane wyjściowe jądra z określonej lokalizacji obrazu pozostały powiązane z tą lokalizacją. Jednak w przeciwieństwie do wymiarów przestrzennych obrazu ten dodatkowy „wymiar jądra” nie ma żadnych właściwości sąsiedztwa, więc nie ma sensu przeprowadzać wzdłuż niego splotów. CNN zostały pierwotnie zainspirowane modelami kory wzrokowej zakorzenionymi w neuronauce. W tych modelach pole receptywne neuronu jest częścią bodźców czuciowych, które mogą wpływać na aktywację tego neuronu. W CNN pole receptywne jednostki w pierwszej ukrytej warstwie jest małe — tylko rozmiar jądra, tj. l pikseli. W głębszych warstwach sieci może być znacznie większy. Rysunek ilustruje to dla jednostki w drugiej warstwie ukrytej, której pole receptywne zawiera pięć pikseli
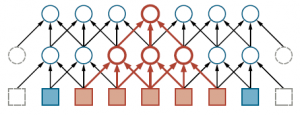
Gdy krok wynosi 1, jak na rysunku, węzeł w m-tej warstwie ukrytej będzie miał pole receptywne o rozmiarze (l -1)m+1; więc wzrost jest liniowy wm. (W obrazie 2D każdy wymiar pola receptywnego rośnie liniowo z m, więc obszar rośnie kwadratowo.) Gdy krok jest większy niż 1, każdy piksel w warstwie m reprezentuje s pikseli w warstwie m-1; dlatego pole receptywne rośnie jako O(lsm) – to znaczy wykładniczo wraz z głębokością. Ten sam efekt występuje w przypadku warstw puli, które omówimy dalej.
Kamuflaż to stan, w którym dwa obiekty tego samego koloru nakładają się na siebie w kadrze i utrudniają wykrycie rzeczywistego obiektu. Na przykład w rolnictwie wykrywanie owadów jest trudne, gdy zwierzęta są tego samego koloru co ich tło liściaste lub kwieciste. Wielu badaczy w tej dziedzinie pracowało nad zmniejszeniem tego, ucząc się reprezentacji poruszających się obiektów, ale nadal jest to duże wyzwanie w obszarze wykrywania i śledzenia obiektów
Podczas procesu uczenia sieć neuronowa pokazuje wiele wartości wejściowych x i wiele odpowiadających im wartości wyjściowych y. Podczas przetwarzania wektora wejściowego x sieć neuronowa wykonuje kilka obliczeń pośrednich przed wygenerowaniem wyniku y. Możemy myśleć o wartościach obliczonych na każdej warstwie sieci jako o innej reprezentacji wejściowego x. Każda warstwa przekształca reprezentację utworzoną przez poprzednią warstwę w celu utworzenia nowej reprezentacji. Zestawienie wszystkich tych przekształceń udaje się — jeśli wszystko pójdzie dobrze — przekształcenia danych wejściowych w pożądane dane wyjściowe. Rzeczywiście, jedną z hipotez wyjaśniających, dlaczego uczenie głębokie działa dobrze, jest to, że złożona, kompleksowa transformacja, która odwzorowuje od wejścia do wyjścia – powiedzmy od obrazu wejściowego do kategorii wyników „żyrafa” – jest rozkładana na wiele warstw w kompozycji. wielu stosunkowo prostych przekształceń, z których każda jest dość łatwa do nauczenia przez lokalny proces aktualizacji. W procesie tworzenia wszystkich tych wewnętrznych przekształceń głębokie sieci często odkrywają znaczące pośrednie reprezentacje danych. Na przykład sieć ucząca się rozpoznawania złożonych obiektów na obrazach może tworzyć wewnętrzne warstwy, które wykrywają przydatne podjednostki: krawędzie, narożniki, elipsy, oczy, twarze – koty. A może nie – głębokie sieci mogą tworzyć wewnętrzne
warstwy, których znaczenie jest dla ludzi niejasne, mimo że wynik jest nadal poprawny. Ukryte warstwy sieci neuronowych są zazwyczaj mniej zróżnicowane niż warstwy wyjściowe. Przez pierwsze 25 lat badań nad sieciami wielowarstwowymi (mniej więcej 1985–2010) węzły wewnętrzne wykorzystywały prawie wyłącznie funkcje aktywacji sigmoid i tanh. Od około 2010 r. ReLU i softplus stają się bardziej popularne, częściowo dlatego, że uważa się, że unikają problemu znikania gradientów. Eksperymenty z coraz głębszymi sieciami sugerowały, że w wielu przypadkach lepsze uczenie uzyskano z głębokimi i stosunkowo wąskimi sieciami, a nie płytkimi, szerokimi sieciami, przy ustalonej łącznej liczbie wag. Jest oczywiście wiele innych struktur, które należy wziąć pod uwagę przy grafach obliczeniowych, oprócz zabawy z szerokością i głębokością. Niewiele wiadomo, dlaczego niektóre struktury wydają się działać lepiej niż inne w przypadku konkretnego problemu. Dzięki doświadczeniu praktycy nabierają intuicji, jak projektować sieci i jak je naprawiać, gdy nie działają, podobnie jak szefowie kuchni zyskują intuicję, jak projektować przepisy i jak je naprawiać, gdy smakują nieprzyjemnie. Z tego powodu narzędzia ułatwiające szybką eksplorację i ocenę różnych struktur są niezbędne do odniesienia sukcesu w rzeczywistych problemach.
Dzięki zastosowaniu modelowania tła, jeśli nie ma dostępnej ramki jako tła, algorytmy mają trudności z wykryciem oryginalnego obiektu. Dlatego bardzo dużym wyzwaniem jest modelowanie tła w takich przypadkach
Po stronie wyjściowej sieci problem kodowania nieprzetworzonych wartości danych do wartości rzeczywistych y dla węzłów wyjściowych grafu jest podobny do problemu kodowania danych wejściowych. Na przykład, jeśli sieć próbuje przewidzieć zmienną Weather , która ma wartości {słońce; deszcz; chmura; śnieg}, użylibyśmy kodowania one-hot z czterema bitami. Tyle o wartościach danych y. A co z przewidywaniem 
dealnie, dokładnie odpowiadałoby to pożądanej wartości y, a strata byłaby zerowa i skończylibyśmy. W praktyce to rzadko się to zdarza – zwłaszcza zanim zaczęliśmy proces dostosowywania ciężarów! Dlatego musimy zastanowić się, co oznacza nieprawidłowa wartość wyjściowa i jak zmierzyć stratę. Wyprowadzając gradienty w równaniach, rozpoczęliśmy od funkcji straty błędu kwadratowego. Dzięki temu algebra jest prosta, ale nie jest to jedyna możliwość. W rzeczywistości w przypadku większości aplikacji głębokiego uczenia bardziej powszechne jest interpretowanie wartości wyjściowych „y jako” prawdopodobieństwa i użyć ujemnego logarytmu prawdopodobieństwa jako funkcji straty – dokładnie tak, jak zrobiliśmy to z uczeniem o maksymalnej wiarygodności . Uczenie o maksymalnej wiarygodności znajduje wartość w, która maksymalizuje prawdopodobieństwo obserwowanych danych. A ponieważ funkcja logarytmiczna jest monotoniczna, jest to równoważne maksymalizacji prawdopodobieństwa logarytmicznego danych, co z kolei jest równoważne minimalizacji funkcji straty zdefiniowanej jako logarytm prawdopodobieństwa ujemnego. (Przypomnij sobie , że rejestrowanie logów zamienia iloczyny prawdopodobieństw na sumy, które są bardziej podatne na obliczanie pochodnych). Innymi słowy, szukasz w, które minimalizuje sumę prawdopodobieństw logarytmu ujemnego N przykładów:
W literaturze dotyczącej głębokiego uczenia często mówi się o minimalizowaniu straty w entropii krzyżowej. Entropia krzyżowa, zapisana jako H(P;Q), jest rodzajem miary niepodobieństwa między dwoma rozkładami P i Q2 Ogólna definicja to
Z założenia funkcja softmax wyprowadza wektor liczb nieujemnych, które sumują się do 1. Jak zwykle, atrament wejściowy do każdego z węzłów wyjściowych będzie ważoną kombinacją liniową wyników z poprzedniej warstwy. Ze względu na wykładniki warstwa softmax akcentuje różnice w wejściach: na przykład, jeśli wektor wejść jest podany przez in=<5,2,0,-2>, to wyjścia mają postać <0.946,;0.047,0. 006,0.001>. Softmax jest jednak płynny i różniczkowalny , w przeciwieństwie do funkcji max. Łatwo wykazać , że esica jest softmaxem z d=2. Innymi słowy, tak jak jednostki sigmoidalne propagują informacje o klasach binarnych przez sieć, jednostki softmax propagują informacje wieloklasowe. W przypadku problemu regresji, w którym wartość docelowa y jest ciągła, często używa się liniowej warstwy wyjściowej – innymi słowy, 
bez żadnej funkcji aktywacji g – i interpretuje to jako średnią prognozy Gaussa ze stałą zmienność. Jak zauważyliśmy na stronie 780, maksymalizacja wiarygodności (tj. minimalizacja prawdopodobieństwa ujemnego logarytmu) za pomocą gaussowskiego o stałej wariancji jest tym samym, co minimalizacja błędu kwadratowego. Tak więc zinterpretowana liniowa warstwa wyjściowa wykonuje klasyczną regresję liniową. Cechami wejściowymi tej regresji liniowej są dane wyjściowe z poprzedniej warstwy, które zazwyczaj wynikają z wielu nieliniowych przekształceń oryginalnych danych wejściowych do sieci. Dostępnych jest wiele innych warstw wyjściowych. Na przykład warstwa gęstości mieszaniny reprezentuje dane wyjściowe przy użyciu mieszaniny rozkładów Gaussa. (Patrz rozdział 21.3.1, aby uzyskać więcej szczegółów na temat mieszanin Gaussa). Takie warstwy przewidują względną częstotliwość każdego składnika mieszaniny, średnią każdego składnika i wariancję każdego składnika. Dopóki te wartości wyjściowe są odpowiednio interpretowane przez funkcję straty jako określającą prawdopodobieństwo dla prawdziwej wartości wyjściowej y, sieć po nauczeniu dopasuje model mieszaniny gaussowskiej w przestrzeni cech określonych przez poprzednie warstwy.
Nadzór wideo jest aktywnym obszarem badań, ale istnieje wiele trudności w uchwyceniu twarzy, niezależnie od tego, czy tło jest statyczne, czy ruchome. Wyzwania mogą dotyczyć m.in. złych warunków pogodowych, efektów świetlnych oraz złej jakości sprzętu. Wyzwania związane z wykrywaniem obiektów mogą pojawić się w dowolnej sekwencji obrazów lub wideo.
Węzły wejściowe i wyjściowe grafu obliczeniowego to te, które łączą się bezpośrednio z danymi wejściowymi x i danymi wyjściowymi y. Kodowanie danych wejściowych jest zwykle proste, przynajmniej w przypadku danych rozkładanych na czynniki, gdzie każdy przykład uczący zawiera wartości dla n atrybutów wejściowych. Jeśli atrybuty są logiczne, mamy n węzłów wejściowych; zwykle fałsz jest mapowany na wejście 0, a prawda jest mapowana na 1, chociaż czasami używane są -1 i +1. Atrybuty numeryczne, zarówno całkowite, jak i rzeczywiste, są zwykle używane bez zmian, chociaż mogą być skalowane tak, aby mieściły się w ustalonym zakresie; jeśli wielkości dla różnych przykładów różnią się ogromnie, wartości można odwzorować na skalę logarytmiczną. Obrazy nie do końca pasują do kategorii danych faktoryzowanych; chociaż obraz RGB o rozmiarze X x Y pikseli można traktować jako atrybuty o wartościach całkowitych 3XY (zazwyczaj z wartościami w zakresie {0,…,255}), to zignoruje to fakt, że tryplety RGB należą do tego samego piksela na obrazie i fakt, że sąsiedztwo pikseli naprawdę ma znaczenie. Oczywiście możemy mapować sąsiednie piksele na sąsiednie węzły wejściowe w sieci, ale znaczenie sąsiedztwa zostaje całkowicie utracone, jeśli wewnętrzne warstwy sieci są w pełni połączone. W praktyce sieci używane z danymi obrazu mają wewnętrzne struktury przypominające tablice, które mają na celu odzwierciedlenie semantyki sąsiedztwa. Zobaczymy Atrybuty kategorialne z więcej niż dwiema wartościami – na przykład atrybut Type w problemie z restauracją , który ma wartości francuskie, włoskie, tajskie lub burgerowe) – są zwykle kodowane przy użyciu tak zwanego kodowania one-hot. Atrybut o d możliwych wartościach jest reprezentowany przez d oddzielnych bitów wejściowych. Dla dowolnej danej wartości odpowiedni bit wejściowy jest ustawiany na 1, a wszystkie pozostałe na 0. Zwykle działa to lepiej niż mapowanie wartości na liczby całkowite. Gdybyśmy użyli liczb całkowitych dla atrybutu Type, Thai miałby wartość 3, a burger byłby 4. Ponieważ sieć jest złożeniem funkcji ciągłych, nie miałaby innego wyjścia, jak zwrócić uwagę na sąsiedztwo liczbowe, ale w tym przypadku na sąsiedztwo liczbowe między Tajska i burgerowa jest semantycznie bez znaczenia.