Miesiąc: sierpień 2022

Rola AI w zapewnianiu efektywności i zwiększaniu korzyści dla dowolnej organizacji lub grupy społecznej jest ogromna. Wraz z nadejściem sztucznej inteligencji świat osiągnął bardziej inteligentne miejsce, którego różne aspekty są badane, testowane i wdrażane w celu zaspokojenia ludzkiego pragnienia poprawy jakości życia. Aby przyspieszyć rozwój sztucznej inteligencji w tych domenach, wymagane są silne, solidne i wydajne języki programowania. Pomogą one w tworzeniu i wdrażaniu aplikacji obsługujących sztuczną inteligencję. Istnieje wiele wyspecjalizowanych języków opracowanych do programowania aplikacji AI. Wyzwanie polega na znalezieniu języka, który zapewni wymagane specyfikacje dla rozwoju sztucznej inteligencji. W tym rozdziale omówiono popularne języki wraz z ich zaletami i wadami, aby badacze w tej dziedzinie mieli gotowe odniesienie. Stwierdzono, że Python, Prolog, Lisp, Java i C++ należą do głównych języków programowania, które można wykorzystać do spełnienia wymagań projektowania i tworzenia różnych aplikacji i oprogramowania AI. W kolejnych podrozdziałach przedstawiono omówienie tych języków programowania, aby programiści i programiści mogli określić, który język będzie odpowiedni dla ich procesu tworzenia oprogramowania.

Argumentowaliśmy wcześniej, że semantyka bazy danych jest odpowiednia w sytuacjach, w których dokładnie znamy zbiór odpowiednich obiektów, które istnieją i możemy je jednoznacznie zidentyfikować. (W szczególności wszystkie obserwacje dotyczące obiektu są poprawnie powiązane ze stałym symbolem, który go nazywa.) Jednak w wielu rzeczywistych warunkach takie założenia są po prostu nie do utrzymania. Na przykład sprzedawca książek może użyć numeru ISBN (International Standard Book Number) jako stałego symbolu nazwy każdej książki, nawet jeśli dana „logiczna” książka (np. „Przeminęło z wiatrem”) może mieć kilka numerów ISBN odpowiadających twardej oprawie , miękka, dużym drukiem, wznowienia i tak dalej. Rozsądne byłoby zbieranie rekomendacji dla wielu numerów ISBN, ale sprzedawca może nie wiedzieć na pewno, które numery ISBN są naprawdę tą samą książką. (Zauważ, że nie potwierdzamy poszczególnych egzemplarzy książki, które mogą być niezbędne do sprzedaży używanych książek, sprzedaży samochodów itd.) Co gorsza, każdy klient jest identyfikowany za pomocą identyfikatora logowania, ale klient nieuczciwy może mieć tysiące identyfikatorów! W dziedzinie bezpieczeństwa komputerowego te liczne identyfikatory nazywane są sybils, a ich użycie do zmylenia systemu reputacji nazywa się atakiem sybil. Tak więc nawet prosta aplikacja w stosunkowo dobrze zdefiniowanej domenie online wiąże się zarówno z niepewnością istnienia (jakie są prawdziwe księgi i klienci leżący u podstaw obserwowanych danych), jak i niepewnością tożsamości (które terminy logiczne rzeczywiście odnoszą się do tego samego obiektu). Zjawiska istnienia i niepewności tożsamości wykraczają daleko poza księgarnie internetowe. W rzeczywistości są wszechobecne:

• System wizyjny nie wie, co istnieje, jeśli w ogóle, za następnym rogiem i może nie wiedzieć, czy obiekt, który widzi teraz, jest tym samym, który widział kilka minut temu.
• System rozumienia tekstu nie zna z góry jednostek, które zostaną przedstawione w tekście i musi uzasadnić, czy wyrażenia takie jak „Mary”, „Dr. Smith, „ona”, „jego kardiolog”, „jego matka” itd. odnoszą się do tego samego obiektu.
• Analityk wywiadu polujący na szpiegów nigdy nie wie, ilu naprawdę jest szpiegów, i może tylko zgadywać, czy różne pseudonimy, numery telefonów i obserwacje należą do tej samej osoby.

Rzeczywiście, znaczna część ludzkiego poznania wydaje się wymagać poznania, jakie obiekty istnieją i umiejętności łączenia obserwacji — które prawie nigdy nie mają dołączonych unikalnych identyfikatorów — z hipotetycznymi obiektami na świecie. Dlatego musimy być w stanie zdefiniować model prawdopodobieństwa otwartego wszechświata (OUPM) oparty na standardowej semantyce logiki pierwszego rzędu. Język jednostek OUPM umożliwia łatwe pisanie takich modeli, gwarantując jednocześnie unikalny, spójny rozkład prawdopodobieństwa w nieskończonej przestrzeni możliwych światów.

W dzisiejszym społeczeństwie sztuczna inteligencja jest wykorzystywana w wielu różnych aplikacjach wykorzystywanych w domach, przemyśle, instytucjach edukacyjnych, transporcie, grach itp. Możliwości sztucznej inteligencji są wykorzystywane przez wiele różnych dziedzin, takich jak instytucje prawne, urzędy patentowe, bankowość, handel detaliczny itp. Sztuczna inteligencja popycha nas w kierunku inteligentnego świata, który poprawia jakość życia. Sztuczna inteligencja opracowana do wykonywania określonych zadań nazywana jest słabą sztuczną inteligencją lub wąską sztuczną inteligencją. Jest używany do wielu rzeczy, takich jak teledetekcja, zautomatyzowane sterowanie, diagnostyka medyczna itp. W tej sekcji omówiono niektóre z tych zastosowań.

AI w rolnictwie

AI może być wykorzystywana w rolnictwie do monitorowania upraw, predykcyjnej analizy pogody, wykrywania chorób w uprawach, zwalczania szkodników, itp. AI pomaga w analizie w czasie rzeczywistym różnych czynników, takich jak klimat, woda i warunki glebowe, aby pomóc rolnikom w podejmowaniu decyzji dotyczących techniki uprawy, wyboru paszy i/lub nawozu itp. Prowadzi to do zwiększenia zbiorów. Wykorzystanie sztucznej inteligencji do poprawy plonów nazywa się rolnictwem precyzyjnym. Inną rolą sztucznej inteligencji jest wykorzystywanie botów do wykonywania tak niebezpiecznych zadań, jak usuwanie chwastów.

AI w bezpieczeństwie

Wraz z dostępnością Internetu i urządzeń korzystających z Internetu nastąpił wzrost cyberprzestępczości. Sztuczna inteligencja odniosła sukces w zapewnianiu bezpieczeństwa danych i zasobów. Dane twarzy mogą być przechwytywane w celu rozpoznawania biometrycznego i analiz w celu uwierzytelnienia. Sztuczna inteligencja jest wykorzystywana w monitoringu wideo do wykrywania ludzi, samochodów i innych obiektów.

AI w edukacji

Instytucje edukacyjne mogą wykorzystywać sztuczną inteligencję na wiele sposobów, takich jak automatyczne ocenianie i wykonywanie rutynowej pracy administratora. Pozwoli to nauczycielom poświęcić więcej czasu na nauczanie i badania. Chatboty AI mogą również odpowiadać na różne pytania studentów. AI może umożliwić każdemu uczniowi pracę indywidualnie, we własnym tempie i zgodnie z własnymi zainteresowaniami.

AI w opiece zdrowotnej

Sztuczna inteligencja ma duży wpływ na opiekę zdrowotną. Umożliwia sprawniejsze i szybsze diagnozowanie chorób. AI może być wykorzystana do opracowania zautomatyzowanej analizy obrazu medycznego. Może analizować duże ilości danych pacjentów w celu identyfikacji pacjentów zagrożonych. Chatboty mogą być rozwijane w celu zapewnienia podstawowej opieki pacjentom na obszarach wiejskich i odległych obszarach .

AI w przemyśle

W produkcji sztuczna inteligencja może być wykorzystywana do wykonywania niektórych powtarzalnych zadań, oszczędzając ludzki czas i wysiłek. Może służyć do analizy preferencji klientów w celu przewidywania trendów w sektorze detalicznym. Może być używany do tworzenia chatbotów, aby pomóc klientom w lepszych i bardziej spersonalizowanych zakupach. Może służyć do przewidywania ryzyka i oszustw w instytucjach finansowych i firmach ubezpieczeniowych. Rola sztucznej inteligencji została wprowadzona w różnych dziedzinach, takich jak opieka zdrowotna, edukacja, samochody autonomiczne, biznes, bezpieczeństwo, rozrywka, gry i symulacje. Wprowadził nas w świat inteligentnych miast Aby uwolnić potencjał i obietnice sztucznej inteligencji w ich prawdziwym znaczeniu, należy opracować wdrożenia na rzecz poprawy społeczeństwa i zastosowań związanych ze stylem życia. Tworzenie aplikacji obsługujących sztuczną inteligencję wymaga odpowiednich języków programowania.

Najprostszym podejściem do wnioskowania w RPM jest po prostu skonstruowanie równoważnej sieci bayesowskiej, biorąc pod uwagę znane symbole stałe należące do każdego typu. W przypadku książek B i klientów C, podstawowy model podany wcześniej mógł być skonstruowany za pomocą prostych pętli:

Ta technika nazywa się uziemieniem lub rozwijaniem; jest to dokładny analog propozycjonalizacji dla logiki pierwszego rzędu. Oczywistą wadą jest to, że uzyskana siatka Bayesa może być bardzo duża. Co więcej, jeśli istnieje wiele obiektów kandydujących do nieznanej relacji lub funkcji — na przykład nieznany autor B₂ – to niektóre zmienne w sieci mogą mieć wielu rodziców. Na szczęście często można uniknąć generowania całej niejawnej sieci Bayesa. Jak widzieliśmy w dyskusji na temat algorytmu eliminacji zmiennych na stronie 451, każda zmienna, która nie jest przodkiem zmiennej zapytania lub zmiennej dowodowej, jest nieistotna dla zapytania. Co więcej, jeśli zapytanie jest warunkowo niezależne od jakiejś zmiennej w danych dowodach, to ta zmienna jest również nieistotna. Tak więc, łącząc model, zaczynając od zapytania i dowodu, możemy zidentyfikować tylko zestaw zmiennych, które są istotne dla zapytania. Są to jedyne, które należy utworzyć, aby utworzyć potencjalnie mały fragment niejawnej sieci Bayesa. Wnioskowanie w tym fragmencie daje taką samą odpowiedź jak wnioskowanie w całej niejawnej sieci Bayesa. Inną drogą poprawy efektywności wnioskowania jest obecność powtarzającej się podstruktury w rozwiniętej sieci Bayesa. Oznacza to, że wiele czynników konstruowanych podczas eliminacji zmiennych (i podobnych rodzajów tabel tworzonych przez algorytmy grupujące) będzie identycznych; efektywne schematy buforowania przyniosły przyspieszenie o trzy rzędy wielkości w dużych sieciach. Po trzecie, algorytmy wnioskowania MCMC mają pewne interesujące właściwości w przypadku zastosowania do RPM z niepewnością relacyjną. MCMC działa poprzez próbkowanie pełnych możliwych światów, więc w każdym stanie struktura relacyjna jest całkowicie znana. W podanym wcześniej przykładzie każdy stan MCMC określiłby wartość Author(B2), a więc inni potencjalni autorzy nie są już rodzicami węzłów rekomendacji dla B2. Dla MCMC zatem niepewność relacyjna nie powoduje wzrostu złożoności sieci; zamiast tego proces MCMC obejmuje przejścia, które zmieniają strukturę relacyjną, a tym samym strukturę zależności, sieci rozwijanej. Wreszcie, w niektórych przypadkach może być możliwe całkowite uniknięcie uziemienia modelu. Dowódcy twierdzeń o rozdzielczości i systemy programowania logicznego unikają tworzenia zdań poprzez tworzenie instancji zmiennych logicznych tylko wtedy, gdy jest to konieczne do przeprowadzenia wnioskowania; to znaczy, podnoszą proces wnioskowania ponad poziom podstawowych zdań zdaniowych i sprawiają, że każdy podniesiony krok wykonuje pracę wielu podstawowych kroków. Ta sama idea może być zastosowana we wnioskowaniu probabilistycznym. Na przykład w algorytmie eliminacji zmiennej zniesiony czynnik może reprezentować cały zestaw czynników podstawowych, które przypisują prawdopodobieństwa zmiennym losowym w obrotach na minutę, gdzie te zmienne losowe różnią się tylko symbolami stałych użytymi do ich skonstruowania.

Sztuczna inteligencja to multidyscyplinarne podejście polegające na włączaniu naturalnej inteligencji do maszyn, aby mogły wykonywać zadania, stosując logikę i rozumowanie. Sztuczna inteligencja ma na celu powielenie ludzkiej inteligencji w urządzeniach komputerowych. Russel i Norvig definiują sztuczną inteligencję jako „badanie agentów, którzy odbierają percepcję z otoczenia i wykonują działania”. W związku z tym istnieją cztery różne sposoby definiowania sztucznej inteligencji, a mianowicie myślenie po ludzku, myślenie racjonalne, postępowanie po ludzku i postępowanie racjonalne. Pierwsze dwa terminy dotyczą wnioskowania i przetwarzania, podczas gdy pozostałe dwa dotyczą aspektów behawioralnych. Techniki sztucznej inteligencji opierają się na regułach, uczeniu maszynowym, uczeniu głębokim itp. W 1943 r. McCullogh i Pitts zaproponowali model budowy sieci neuronowej. Rok 1950 był bardzo ważny dla rozwoju AI. W tym roku Turing zaproponował test Turinga, aby określić, czy maszyna jest inteligentna, czy nie. SNARC (Stochastic Neural Analog Reinforcement Calculator), pierwszy komputer sieci neuronowej, został opracowany i opublikowano w tym roku prawa robotyki. W 1952 Samuel opracował program do samodzielnej nauki gry w szachy. W 1972 opracowano Prolog, język programowania dla AI. W nadchodzących latach opracowano wiele innych technik. W 1955 McCarthy ukuł termin „AI”. W 1974 komputery stały się szybsze i tańsze, co doprowadziło do rozwoju przetwarzania języka naturalnego (NLP). W 1966 roku wprowadzono Elizę, pierwszego chatbota. Pierwszy Expert został opracowany w 1980 roku. W 1997 roku IBM Deep Blue pokonał mistrza świata w szachach. W 2002 roku opracowano odkurzacz o nazwie Roomta. Do 2006 r. organizacje takie jak Facebook, Netflix i inne zaczęły wykorzystywać sztuczną inteligencję w swoich działaniach. Dzięki sztucznej inteligencji urządzenia z oprogramowaniem mogą skutecznie i dokładnie rozwiązywać rzeczywiste problemy . Osobiści wirtualni asystenci, tacy jak Siri, Google Assistant, Cortana i tym podobne, zostali stworzeni za pomocą sztucznej inteligencji. Urządzenia obsługujące sztuczną inteligencję mogą być również wykorzystywane w pracach uznawanych za niebezpieczne dla ludzi, takich jak górnictwo. Sztuczna inteligencja ma kilka zalet, takich jak wysoka dokładność, szybsza prędkość, zoptymalizowana niezawodność itp. Istnieją jednak również pewne problemy związane ze sztuczną inteligencją, takie jak wysoki koszt, brak emocji, tworzenie zależności od maszyny itp. Sztuczna inteligencja jest multidyscyplinarną dziedziną nauki obejmującą nie tylko informatyka, ale także matematyka, biologia, socjologia, statystyka itp.

AI jest bardzo wszechstronna i nie ogranicza się do branży komputerowej. Odgrywa ważną rolę w opiece zdrowotnej, bankowości, nadzorze bezpieczeństwa, przemyśle samochodowym, żeby wymienić tylko kilka. Sztuczna inteligencja prawdopodobnie zastąpi ludzi w wielu zawodach. To są niektóre pozytywne aspekty tego rozwoju, w szczególności eliminacja zagrożenia życia i zdrowia związanego z niektórymi szczególnie niebezpiecznymi zawodami. Jednocześnie jednak rozwój ten prawdopodobnie zwiększy bezrobocie i napięcia społeczno-gospodarcze. Dlatego integracji AI w tych branżach i stanowiskach musi towarzyszyć przekwalifikowanie personelu ludzkiego, aby zainicjować płynne przejścia na rynku pracy. Może ci sami pracownicy mogą nawet zostać przeszkoleni w zakresie obsługi i obsługi technologii opartej na sztucznej inteligencji. Sztuczna inteligencja może być również wykorzystywana do generowania i analizowania ogromnych ilości danych, co prowadzi do lepszych systemów eksperckich i bardziej świadomego kształtowania polityki. Potencjał poprawy ludzkiego życia poprzez sztuczną inteligencję obejmuje również takie rzeczy, jak zarządzanie katastrofami, opieka zdrowotna, rolnictwo, inicjatywy środowiskowe, zapobieganie przestępczości, zarządzanie zasobami itp. Sztuczna inteligencja dodana do urządzeń osobistych, takich jak telefony, obiecuje stworzyć płynniejszy styl życia dzięki korzystanie z asystenta wizualnego, chatbotów itp. Dlatego można zrozumieć, że sztuczna inteligencja odgrywa znaczącą rolę we wszystkich aspektach ludzkiego życia. Tworzone są różne aplikacje w różnych dziedzinach, aby pomóc w podniesieniu ludzkiego życia i przynieść korzyści społeczeństwu. W kolejnej części omówiono rolę AI w różnych dziedzinach, takich jak m.in. rolnictwo, edukacja czy ochrona zdrowia.

Wiele konkurencyjnych gier ma liczbową miarę poziomu umiejętności graczy, czasami nazywaną oceną. Być może najbardziej znanym jest ranking Elo dla szachistów, który typowego początkującego ocenia na około 800, a mistrza świata zwykle gdzieś powyżej 2800. Chociaż rankingi Elo mają podstawę statystyczną, zawierają pewne elementy ad hoc. Możemy opracować schemat oceny Bayesa w następujący sposób: każdy gracz i ma podstawowy poziom umiejętności Umiejętność(i); w każdej grze g rzeczywista wydajność i to Wydajność (i;g), która może różnić się od podstawowego poziomu umiejętności; a zwycięzcą g jest gracz, którego gra w g jest lepsza. Jako RPM model wygląda tak:

gdzie β² to wariancja rzeczywistej wydajności gracza w dowolnej konkretnej grze w stosunku do podstawowego poziomu umiejętności gracza. Mając zestaw graczy i gier, a także wyniki niektórych gier, silnik wnioskowania RPM może obliczyć rozkład a posteriori umiejętności każdego gracza i prawdopodobny wynik każdej dodatkowej gry, w którą można zagrać.

W przypadku gier zespołowych przyjmiemy jako pierwsze przybliżenie, że ogólna wydajność zespołu t w grze g jest sumą indywidualnych występów zawodników na t:

Mimo że poszczególne występy nie są widoczne dla silnika ocen, poziomy umiejętności zawodników można oszacować na podstawie wyników kilku meczów, o ile składy drużyn różnią się w zależności od gry. Silnik oceny TrueSkill firmy Microsoft wykorzystuje ten model wraz z wydajnym algorytmem wnioskowania przybliżonego, aby codziennie obsługiwać setki milionów użytkowników. Model ten można rozwijać na wiele sposobów. Na przykład możemy założyć, że słabsi gracze mają większą rozbieżność w swoich wynikach; możemy uwzględnić rolę gracza w zespole; możemy też rozważyć określone rodzaje wydajności i umiejętności – np. obronę i atak – w celu poprawy składu zespołu i dokładności predykcyjnej.

Sztuczna inteligencja to dziedzina nauki, w której maszynie można nadać zdolność wykonywania zadań za pomocą ludzkiej inteligencji lub rozumowania. Obecnie sztuczna inteligencja jest w stanie grać w gry, pomagać marketerom reklamować się zainteresowanym klientom, odtwarzać muzykę, malować, żeby wymienić tylko kilka zadań. Sztuczna inteligencja realizuje niektóre zadania wymagające dużej wiedzy, stosując ludzką logikę i zdolności rozumowania w połączeniu z silną pracowitością i prawdziwością maszyny. Sztuczna inteligencja oferuje mniejsze prawdopodobieństwo błędu, lepsze standardy wydajności i bardziej efektywne wykorzystanie surowców. Jednak pewnymi wadami sztucznej inteligencji są jej obecne wysokie koszty, zależność od zautomatyzowanych procesów, niemożność wykorzystania emocji w jej działaniu itp. Jeśli sztuczna inteligencja jest wykorzystywana w złośliwy sposób, może powodować spustoszenie na świecie. Obietnice korzyści płynących z używania aplikacji i urządzeń AI nakładają się na koncepcję niewłaściwego wykorzystania AI. Tu przedstawiono przegląd sztucznej inteligencji wraz z jej rolą w różnych obszarach. Jednym z przykładów popularnych aplikacji AI jest Smart Assistant, taki jak Alexa i Siri. Omówiono również różne języki programowania używane w AI, wraz z ich zaletami i wadami

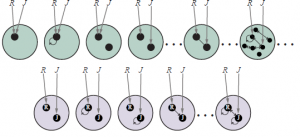
Zacznijmy od prostego przykładu: załóżmy, że sprzedawca książek online chciałby przedstawić ogólną ocenę produktów na podstawie rekomendacji otrzymanych od swoich klientów. Ocena przybierze formę późniejszego rozkładu jakości książki, biorąc pod uwagę dostępne dowody. Najprostszym rozwiązaniem jest oparcie oceny na średniej rekomendacji, być może z wariancją determinowaną liczbą rekomendacji, ale nie uwzględnia to faktu, że niektórzy klienci są życzliwsi od innych, a niektórzy mniej uczciwi niż inni. Uprzejmi klienci zwykle dają wysokie rekomendacje nawet dość przeciętnym książkom, podczas gdy nieuczciwi klienci dają bardzo wysokie lub bardzo niskie rekomendacje z powodów innych niż jakość — mogą być opłacani za promowanie niektórych książek wydawców. Dla pojedynczego klienta C₁ polecającego pojedynczą książkę B₁, sieć Bayesa może wyglądać jak ta pokazana na rysunku (a).

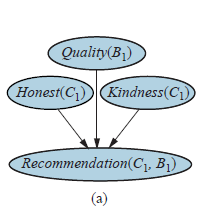
(Wyrażenia z nawiasami, takie jak Honest(C₁), są po prostu fantazyjnymi symbolami – w tym przypadku fantazyjnymi nazwami zmiennych losowych.) Z dwoma klientami i dwiema książkami, sieć Bayesa wygląda jak ta na rysunku 18.2( b). W przypadku większej liczby książek i klientów ręczne określanie sieci Bayesa jest dość niepraktyczne. Na szczęście sieć ma dużo powtarzalnej struktury. Każda zmienna Rekomendacja(c;b) ma rodzicami zmienne Honest(c), Kindness(c) i Quality(b). Co więcej, tabele prawdopodobieństwa warunkowego (CPT) dla wszystkich zmiennych Rekomendacja(c;b) są identyczne, podobnie jak te dla wszystkich zmiennych Honest(c) i tak dalej. Sytuacja wydaje się być dostosowana do języka pierwszego rzędu. Chcielibyśmy powiedzieć coś w stylu

Rekomendacja(c;b) ~ RecCPT(Uczciwy(c);Uprzejmość(c);Jakość(b))

co oznacza, że ​​rekomendacja książki przez klienta zależy prawdopodobnie od uczciwości i życzliwości klienta oraz jakości książki według ustalonego CPT. Podobnie jak logika pierwszego rzędu, RPM mają symbole stałych, funkcji i predykatów. Przyjmiemy również sygnaturę typu dla każdej funkcji — to znaczy specyfikację typu każdego argumentu i wartości funkcji. (Jeżeli znany jest typ każdego obiektu, wiele fałszywych możliwych światów jest eliminowanych przez ten mechanizm; na przykład nie musimy się martwić o życzliwość każdej książki, książki polecające klientów itd.) W przypadku domeny rekomendacji książek, typy to Klient i Książka, a sygnatury typów dla funkcji i predykatów  są następujące:

Uczciwy : Klient -> {true; false}

Życzliwość: Klient-> {1,2,3,4,5}

Jakość : Książka -> {1,2,3,4,5}

Rekomendacja: Księga x Klienta -> {1;2;3;4;5}

Symbolami stałymi będą wszystkie nazwy klientów i książek, które pojawiają się w zestawie danych sprzedawcy. W przykładzie przedstawionym na rysunku (b) były to C₁, C₂ i B₁, B₂.

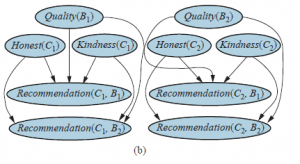
Biorąc pod uwagę stałe i ich typy, wraz z funkcjami i ich sygnaturami typów, podstawowe zmienne losowe RPM uzyskuje się poprzez utworzenie instancji każdej funkcji z każdą możliwą kombinacją obiektów. W przypadku modelu rekomendacji książek podstawowe zmienne losowe obejmują Uczciwość(C₁), Jakość(B₂), Rekomendację(C₁,B₂) i tak dalej. Są to dokładnie te zmienne, które pojawiają się na rysunku (b). Ponieważ każdy typ ma tylko skończenie wiele instancji (dzięki założeniu domknięcia domeny), liczba podstawowych zmiennych losowych również jest skończona. Aby ukończyć RPM, musimy napisać zależności, które rządzą tymi zmiennymi losowymi. Dla każdej funkcji istnieje jedna instrukcja zależności, gdzie każdy argument funkcji jest zmienną logiczną (tj. zmienną, która obejmuje obiekty, jak w logice pierwszego rzędu). Na przykład poniższa zależność stwierdza, że ​​dla każdego klienta c prawdopodobieństwo a priori uczciwości wynosi 0,99 prawdziwe, a 0,01 fałszywe:

Uczciwy(c) ~ <0:99;0:01>

Podobnie możemy określić wcześniejsze prawdopodobieństwa wartości życzliwości każdego klienta i jakości każdej książki, każde w skali 1-5:

Życzliwość(c) ~ <0:1;0:1;0:2;0:3;0:3>

Jakość(b) ~ <0:05;0:2;0:4;0:2;0:15>

Na koniec potrzebujemy zależności dla rekomendacji: dla każdego klienta c i książki b wynik zależy od uczciwości i życzliwości klienta oraz jakości książki: Rekomendacja(c;b) RecCPT(Honest(c); Kindness (c); Jakość(b)) gdzie RecCPT jest oddzielnie zdefiniowaną tabelą prawdopodobieństwa warunkowego z 2  x 5 x 5=50 wierszami, każdy z 5 wpisami. Dla ilustracji przyjmiemy, że uczciwa rekomendacja książki o jakości q od osoby życzliwej k jest równomiernie rozłożona w zakresie

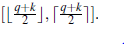
Semantykę RPM można uzyskać przez utworzenie instancji tych zależności dla wszystkich znanych stałych, dając sieć bayesowską (jak na rysunku (b)), która definiuje łączny rozkład zmiennych losowych RPM. Zbiór światów możliwych jest iloczynem kartezjańskim zakresów wszystkich podstawowych zmiennych losowych i, podobnie jak w przypadku sieci bayesowskich, prawdopodobieństwo dla każdego świata możliwego jest iloczynem odpowiednich prawdopodobieństw warunkowych z modelu. W przypadku klientów C i książek B istnieją zmienne C Honest, C Kindness, zmienne jakości B i zmienne rekomendacji BC, prowadzące do możliwych światów 2^C5^C+B+BC. Z dziesięcioma milionami książek i miliardem klientów to około 10^7×1015 światów. Dzięki wyrazistej sile RPM, kompletny model prawdopodobieństwa nadal ma tylko mniej niż 300 parametrów – większość z nich znajduje się w tabeli RecCPT. Możemy udoskonalić model poprzez zapewnienie niezależności zależnej od kontekstu ( aby odzwierciedlić fakt, że nieuczciwi klienci ignorują jakość podczas wydawania rekomendacji; ponadto życzliwość nie odgrywa żadnej roli w ich decyzjach. Zatem Rekomendacja(c;b) jest niezależna od Uprzejmości(c) i Jakości(b), gdy Uczciwy(c)=false:

Rekomendacja(c;b) ~ jeśli Uczciwy(c) to

UczciwyRecCPT (życzliwość (c); jakość (b))

w przeciwnym razie <0.4,0.1,0.0,0.1,0.4> :

Ten rodzaj zależności może wyglądać jak zwykła instrukcja if-then-else w języku programowania, ale istnieje kluczowa różnica: silnik wnioskowania niekoniecznie zna wartość testu warunkowego, ponieważ Honest(c) jest zmienną losową . Możemy rozwijać ten model na nieskończone sposoby, aby był bardziej realistyczny. Załóżmy na przykład, że uczciwy klient, który jest fanem autora książki, zawsze daje książce 5, niezależnie od jakości:

Rekomendacja(c;b) ~ jeśli Uczciwy(c) to

jeśli Fan(c;Autor(b)) to Dokładnie(5)

w przeciwnym razie HonestRecCPT (życzliwość (c); jakość (b))

w przeciwnym razie <0.4,0.1,0.0,0.1,0.4>

Ponownie, test warunkowy Fan(c;Autor(b)) jest nieznany, ale jeśli klient daje tylko 5s książkom konkretnego autora i nie jest poza tym szczególnie uprzejmy, wtedy prawdopodobieństwo późniejszego, że klient jest fanem tego autora będzie być na haju. Ponadto dystrybucja a posteriori będzie miała tendencję do dyskontowania 5 klientów w ocenie jakości książek tego autora. W tym przykładzie domyślnie założyliśmy, że wartość Autor(b) jest znana dla każdego b, ale może tak nie być. Jak system może uzasadnić, czy, powiedzmy, C₁ jest fanem Autora(B₂), gdy Autor(B₂) jest nieznany? Odpowiedź brzmi, że system może być zmuszony do uzasadnienia wszystkich możliwych autorów. Załóżmy (dla uproszczenia), że jest tylko dwóch autorów, A₁ i A₂. Wtedy Autor(B₂) jest zmienną losową z dwiema możliwymi wartościami, A₁ i A₂ i jest rodzicem Rekomendacji(C₁,B₂). Zmienne Fan(C₁,A₁) i Fan(C₁,A₂) są też rodzicami. Rozkład warunkowy dla Rekomendacji(C₁,B₂) jest zatem zasadniczo multiplekserem, w którym rodzic Author(B₂) działa jako selektor, aby wybrać, który z Fan(C₁ ,A₁) i Fan(C₁,A₂) faktycznie ma wpływ na rekomendację . Niepewność wartości Author(B₂), która wpływa na strukturę zależności sieci, jest przykładem niepewności relacyjnej. Jeśli zastanawiasz się, w jaki sposób system może ustalić, kto jest Author(B₂), rozważ możliwość, że trzech innych klientów jest fanami A₁ (i nie ma innych wspólnych ulubionych autorów) i wszyscy trzej przyznali B₂ ocenę 5, mimo że większość innych klientów uważa to za dość ponure. W takim przypadku jest bardzo prawdopodobne, że autorem B₂ jest A₁. Pojawienie się tak wyrafinowanego rozumowania z zaledwie kilku linijek modelu RPM jest intrygującym przykładem tego, jak probabilistyczne wpływy rozprzestrzeniają się poprzez sieć powiązań między obiektami w modelu. W miarę dodawania większej liczby zależności i większej liczby obiektów obraz przekazywany przez rozkład a posteriori często staje się coraz wyraźniejszy.

Jeśli chodzi o maszyny, wszystkie rzeczy wykonywane przez ludzi określa się mianem reprezentacji wiedzy i rozumowania (KRR). Jest to segment sztucznej inteligencji, który zajmuje się myśleniem o agentach AI i tym, jak przyczynia się do inteligentnego zachowania agenta. Ten rozdział zawiera podstawowy przegląd reprezentacji wiedzy (KR) i tego, w jaki sposób jest ona pomocna w demonstrowaniu inteligentnego zachowania w różnych rodzajach wiedzy agenta AI, a także relacji między inteligencją a wiedzą. W tym rozdziale przedstawiono szczegółowy przegląd cyklu życia wiedzy w AI, podstawowe wymagania dotyczące systemu reprezentacji wiedzy (KR) oraz różne techniki i trudne zagadnienia KR.

Przypomnijmy, że model prawdopodobieństwa definiuje zbiór W możliwych światów o prawdopodobieństwie P(ω) dla każdego świata ω. W przypadku sieci bayesowskich możliwe światy to przypisania wartości do zmiennych; w szczególności w przypadku Boole’a możliwe są światy: identyczne z logiką zdań. W przypadku modelu prawdopodobieństwa pierwszego rzędu wydaje się zatem, że potrzebujemy możliwych światów logiki pierwszego rzędu, to znaczy zbioru obiektów z relacjami między nimi i interpretacji, która odwzorowuje stałe symbole na obiekty, predykaty symboli do relacje i symbole funkcyjne do funkcji na tych obiektach. Model musi również zdefiniować prawdopodobieństwo dla każdego takiego możliwego świata, tak jak sieć bayesowska definiuje prawdopodobieństwo dla każdego przypisania wartości do zmiennych. Załóżmy na chwilę, że wymyśliliśmy, jak to zrobić. Następnie, jak zwykle, możemy otrzymać prawdopodobieństwo dowolnego zdania logicznego pierwszego rzędu φ (phi) jako sumę dla możliwych światów, w których jest prawdziwe:

Prawdopodobieństwa warunkowe P(φ|e) można otrzymać w podobny sposób, więc możemy w zasadzie zadać dowolne pytanie dotyczące naszego modelu – i uzyskać odpowiedź. Na razie w porządku. Jest jednak pewien problem: zbiór modeli pierwszego rzędu jest nieskończony. Widzimy to wyraźnie na rysunku (u góry). Oznacza to, że (1) sumowanie w równaniu (18.1) może być niewykonalne, oraz (2) określenie pełnego, spójnego rozkładu na nieskończony zbiór światów może być bardzo trudne.

W tej sekcji unikamy tego problemu, biorąc pod uwagę semantykę bazy danych zdefiniowaną wcześniej. Semantyka bazy danych zakłada założenie unikalnych nazw – tutaj przyjmujemy ją dla stałych symboli. Zakłada również zamknięcie domeny – nie ma więcej obiektów poza tymi, które są nazwane. Możemy wtedy zagwarantować skończony zbiór możliwych światów, czyniąc zbiór obiektów w każdym świecie dokładnie zbiorem stałych symboli, które są używane; jak pokazano na rysunku (na dole), nie ma niepewności co do mapowania symboli na obiekty lub co do istniejących obiektów. Modele zdefiniowane w ten sposób nazwiemy relacyjnymi modelami prawdopodobieństwa, czyli RPM.1 Najważniejszą różnicą między semantyką RPM a semantyką baz danych jest to, że RPM nie dokonują założenia o zamkniętym świecie – w probabilistycznym rozumowania nie możemy po prostu założyć, że każdy nieznany fakt jest fałszywy.