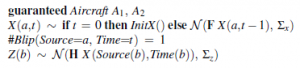W tej sekcji przedstawiono studium przypadku dotyczące klasyfikacji danych ROSIS-3 przy użyciu podejścia opartego na ML.
Architektura podejścia opartego na ML składa się z następujących elementów:
Ilustrujemy to podejście do modelowania i wnioskowania probabilistycznego poprzez problem napisania programu, który odczytuje zdegradowany tekst. Tego rodzaju modele mogą być zbudowane do czytania tekstu, który został rozmazany lub rozmazany z powodu zalania wodą lub zaplamiony z powodu starzenia się papieru, na którym jest drukowany. Można je również zbudować do łamania niektórych rodzajów CAPTCHA. Poniżej przedstawiamy program generatywny zawierający dwa komponenty: (i) sposób generowania ciągu liter; oraz (ii) sposób generowania hałaśliwego, rozmytego renderowania tych liter przy użyciu gotowej biblioteki graficznej.
ysunek pokazuje przykładowe obrazy wygenerowane przez dziewięciokrotne wywołanie funkcji GENERATE-IMAGE.
Cyfrowe przetwarzanie obrazu polega na wykorzystaniu informacji numerycznych na obrazach, aby były one bardziej odpowiednie do interpretacji wizualnej i przetwarzania cyfrowego. Techniki i podejścia do przetwarzania obrazu są dobrze ugruntowane ze względu na łatwy dostęp i dostępność potężnych systemów komputerowych, urządzeń pamięci masowej, oprogramowania itp. Jednak pomimo licznych postępów w technologii obrazowania obrazy optyczne rejestrowane przez bardzo czułe czujniki często wymagają zaawansowanego przetwarzania techniki do zbadania . Cyfrowe przetwarzanie obrazów satelitarnych jest jedną z podstawowych czynności w obszarach zastosowań RS, takich jak rolnictwo, leśnictwo, ekologia, zarządzanie katastrofami i tak dalej. Niemniej jednak przetwarzanie obrazu staje się skomplikowane ze względu na ogromne rozmiary obrazów RS. Pomimo złożoności aplikacji, niektóre podstawowe techniki są powszechne w aplikacjach wykrywających RS . Klasyfikacja danych RS stała się podstawowym i uniwersalnym narzędziem monitorowania zasobów środowiska i zasobów naturalnych w ciągu ostatnich kilkudziesięciu lat. Typowy system klasyfikacji tworzony jest w oparciu o rozdzielczość spektralno-przestrzenną danych RS, wybór algorytmów przetwarzania obrazu i klasyfikacji, kryteria klasyfikacji użytkownika oraz ograniczenia czasowe. Wystarczająca liczba próbek prawdy podstawowej w odniesieniu do każdej z interesujących nas klas ma krytyczne znaczenie dla klasyfikacji RS . Próbki uczące są w większości generowane na podstawie piksela, aby zmniejszyć nadmiarowość i autokorelację między docelowymi klasami . Jednak trudno jest zbierać próbki uczące, gdy scena jest bardzo złożona i niejednorodna, dlatego wybór próbek prawdy podstawowej musi uwzględniać rozdzielczość przestrzenną i spektralną wykorzystywanych danych RS, łatwość użycia danych referencyjnych naziemnych oraz złożoność. terenu i krajobrazów na badanym obszarze . Analizę danych RS przeprowadza się przy użyciu różnych technik przetwarzania obrazu. Większość z tych procesów obejmuje identyfikację i odtwarzanie wadliwych linii, korekcję geometryczną lub georeferencję, korekcję radiometrii obrazu oraz korekcję błędów wywołanych przez parametry atmosferyczne i topograficzne. Korekta atmosferyczna nie jest wymagana, gdy korzystamy z jednodatowych danych RS , ale jest obowiązkowa, jeśli badanie wymaga danych wieloczasowych lub wieloczujnikowych. Doniesiono o ogromnej liczbie metod wstępnego przetwarzania obrazów do korekcji i normalizacji błędów radiometrycznych i atmosferycznych. Rektyfikacja topograficzna to kolejna ważna kwestia, jeśli badany obszar znajduje się na terenie pagórkowatym. Konwencjonalne popularne klasyfikatory „twarde” często wiążą się z problemem spowodowanym mieszaniem pikseli . Mają one znaczną złożoność w radzeniu sobie z obrazami wielowymiarowymi o większej wariancji treści; okazują się niespójne pod względem zdolności przewidywania i nie identyfikują obiektu zainteresowania. Zgłoszono poważną słabość tradycyjnych klasyfikatorów. Klasyfikatory nieparametryczne oparte na ML są traktowane jako najbardziej odpowiednie podejścia w RS do klasyfikacji danych wieloźródłowych. Istnieje wiele problemów i wyzwań związanych z przetwarzaniem hiperspektralnego obrazu RS w porównaniu z wielospektralnym obrazem RS, ponieważ obrazy hiperspektralne mają ogromną liczbę pasm widmowych zawierających ogromne ilości informacji. Wymaga bardziej wyrafinowanych technik, aby uniknąć zjawiska Hughesa, a także zminimalizować złożoność obliczeniową wywołaną wyższym wymiarem widmowym obrazów hiperspektralnych. Identyfikacja nadmiarowych i zaszumionych pasm jest bardzo istotna, a wybór odpowiednich i nieskorelowanych pasm widmowych jest jednym z głównych zadań podczas fazy przetwarzania wstępnego. Wybór odpowiedniego zestawu cech lub atrybutów był istotny dla uzyskania wyższej dokładności klasyfikacji. Jak donosi obszernie w literaturze, eliminacja niepotrzebnych lub zaszumionych pasm jest kluczem do uzyskania ulepszonego podejścia do klasyfikacji; jednak proces ten może pogorszyć wynik klasyfikacji. Wiele źródeł sugeruje zaawansowane techniki w celu radzenia sobie ze zjawiskami Hughesa, ale nadal jest to ważna kwestia, której nie można przeoczyć podczas klasyfikacji. Wybór odpowiednich pasm do kilku zastosowań wymaga szczególnego rozważenia; jest to jednak zasadnicza kwestia w przetwarzaniu obrazów hiperspektralnych. Zwykle obszar zainteresowania zawiera jedną lub więcej podobnych spektralnie cech, które są trudne do zdefiniowania za pomocą pojedynczej funkcji gęstości Gaussa, stąd większość udanych klasyfikatorów wielospektralnych nie osiąga dobrej dokładności. Przetwarzanie ogromnej liczby pasm hiperspektralnych wpływa również na wydajność obliczeniową systemu klasyfikacji, co może prowadzić do niespójności wyników w wielu zastosowaniach
Wiele probabilistycznych języków programowania zostało zbudowanych na spostrzeżeniu, że modele prawdopodobieństwa można zdefiniować za pomocą kodu wykonywalnego w dowolnym języku programowania, który zawiera źródło losowości. W przypadku takich modeli możliwe światy są śladami wykonania, a prawdopodobieństwo takiego śladu jest prawdopodobieństwem losowych wyborów wymaganych do zaistnienia tego śladu. Stworzone w ten sposób PPL dziedziczą całą moc ekspresji języka bazowego, w tym złożone struktury danych, rekurencję i, w niektórych przypadkach, funkcje wyższego rzędu. Wiele PPL jest w rzeczywistości uniwersalnych obliczeniowo: mogą reprezentować dowolny rozkład prawdopodobieństwa, z którego może pobrać próbkę probabilistyczna maszyna Turinga, która się zatrzymuje.
Tradycyjnie przetwarzanie obrazu to proces ulepszania obrazu lub wydobywania znaczących informacji. Koncentruje się bardziej na rozwoju technik ekstrakcji cech stosowanych do statystycznej klasyfikacji obrazów wizualnych. Wraz z szybkim rozwojem technologii informatycznych rośnie stopniowo zapotrzebowanie na technologię przetwarzania obrazu, co daje podstawę do obsługi różnych aplikacji przetwarzania obrazu. Większość technik przetwarzania obrazu opiera się na teorii matematycznej i statystycznej. Przetwarzanie obrazu można traktować jako proces obliczeniowy charakteryzujący się zestawem algorytmów wykorzystywanych do przetwarzania surowych obrazów otrzymywanych z czujników kosmicznych lub powietrznych, a nawet zdjęć wykonanych za pomocą smartfonów. Przetwarzanie obrazu ma szeroki zakres zastosowań w dziedzinie elektroniki i telekomunikacji, nauk medycznych, teledetekcji (RS), biotechnologii, robotyki itp. Naukowcy próbowali opracować techniki analizy obrazu tak skuteczne, jak dla wielu ludzi system wizyjny. dekady. Do tej pory opracowano i opracowano wiele algorytmów i technik, które obejmują różne etapy technik przetwarzania i rozpoznawania obrazów. W szczególności technologia RS okazała się bardzo ważnym i szeroko rozpowszechnionym instrumentem w agencjach rządowych i branżach służącym do zarządzania zasobami naturalnymi i działań monitorujących. Obszar ten wzbudził duże zainteresowanie badaczy postępem technik przetwarzania obrazu. Postęp w technologii czujników i konstelacji satelitów obserwujących Ziemię na całym świecie dał ogromne możliwości w modelowaniu powierzchni Ziemi w celu skutecznego wykrywania zmian i monitorowania. Dostępność obrazów RS o wysokiej rozdzielczości przyniosła nowe wyzwania i możliwości w zakresie rozwoju zaawansowanych technik przetwarzania obrazów do monitorowania i wykrywania zmian. Pozwala władzom na monitorowanie i wykrywanie zmian w dynamice krajobrazu, w tym na obszarach ogólnie niedostępnych lub niebezpiecznych. W terminologii ML klasyfikację można zdefiniować jako problem identyfikacji nowej obserwacji do zbioru predefiniowanych obserwacji na podstawie zbioru uczących zbiorów danych. Aktualna literatura ujawniła niezwykły potencjał technik opartych na sztucznej inteligencji w obszarze przetwarzania obrazów RS. Wcześniej powszechnie uznane konwencjonalne techniki i modele zostały zdominowane przez lepsze metody obróbki wstępnej i klasyfikacji. Rosnący profil technik uczenia maszynowego i głębokiego uczenia (DL) zwrócił dużą uwagę na rozwiązywanie szerokiego zakresu zadań pojawiających się w przetwarzaniu i klasyfikacji obrazów, wykrywaniu obiektów i segmentacji obrazów. Techniki klasyfikacji oparte na ML, głównie losowy las (RF), sztuczna sieć neuronowa (ANN), maszyna wektorów nośnych (SVM) i oparte na rozmytym uczeniu adaptacyjnym, zdominowały inne konwencjonalne klasyfikatory w klasyfikacji teledetekcyjnej. Mają ogromny potencjał w klasyfikowaniu danych VHR, ponieważ biorą pod uwagę zarówno spektralne, jak i przestrzenne cechy morfologiczne obrazu do predykcji. Obecnie podejścia do klasyfikacji zespołowej okazały się bardzo skuteczne w zastosowaniach do wykrywania wzorców i obiektów, ponieważ metoda zespołowa wykorzystuje zestaw klasyfikatorów bazowych, aby osiągnąć wyższą zdolność predykcyjną niż konwencjonalny klasyfikator. W niniejszym rozdziale przedstawiono zagadnienia i wyzwania technik przetwarzania obrazu w odniesieniu do klasyfikacji zbiorów danych VHR RS. Przedstawiono studium przypadku dotyczące klasyfikacji obrazów z czujnika hiperspektralnego Airborne ROSIS-3 przy użyciu podejścia opartego na ML. Przedstawiono uwagi końcowe w kierunku klasyfikacji danych VHR RS przy użyciu technik DL.
Rysunek przedstawia dwa obrazy z szeroko oddzielonych kamer na autostradzie w Kalifornii.
W tej aplikacji interesują nas dwa cele: oszacowanie czasu potrzebnego, przy aktualnych warunkach ruchu, na przejście z jednego miejsca do drugiego w systemie autostrad; oraz mierzenie popytu — to znaczy, ile pojazdów porusza się między dowolnymi dwoma punktami w systemie o określonych porach dnia iw określonych dniach tygodnia. Oba cele wymagają rozwiązania problemu powiązania danych na dużym obszarze z wieloma kamerami i dziesiątkami tysięcy pojazdów na godzinę. W przypadku nadzoru wizualnego fałszywe alarmy są powodowane przez poruszające się cienie, pojazdy przegubowe, odbicia w kałużach itp.; niepowodzenia wykrywania są spowodowane okluzją, mgłą, ciemnością i brakiem kontrastu wizualnego; a pojazdy stale wjeżdżają i wyjeżdżają z systemu autostrad w punktach, które mogą nie być monitorowane. Co więcej, wygląd dowolnego pojazdu może się radykalnie zmieniać między kamerami w zależności od warunków oświetleniowych i pozycji pojazdu na obrazie, a model przejścia zmienia się wraz z pojawianiem się i znikaniem korków. Wreszcie, w gęstym ruchu z szeroko oddzielonymi kamerami, błąd przewidywania w modelu przejściowym dla samochodu jadącego z jednej lokalizacji kamery do drugiej jest znacznie większy niż typowy odstęp między pojazdami. Pomimo tych problemów, nowoczesne algorytmy asocjacji danych odniosły sukces w szacowaniu parametrów ruchu w warunkach rzeczywistych. Asocjacja danych jest niezbędnym fundamentem śledzenia złożonego świata, ponieważ bez niego nie ma możliwości połączenia wielu obserwacji dowolnego obiektu. Kiedy obiekty na świecie wchodzą ze sobą w interakcje w złożonych działaniach, zrozumienie świata wymaga połączenia powiązania danych z relacyjnymi modelami prawdopodobieństwa otwartego wszechświata. Jest to obecnie aktywny obszar badań.
Pojawienie się sztucznej inteligencji obiecuje zmiany, które przenikną do podstaw ludzkiego stylu życia, wprowadzając zmiany w różnych dziedzinach, takich jak media, opieka zdrowotna, produkcja, handel detaliczny, usługi komunalne, motoryzacja itp. Dlatego bardzo zrozumiałe jest poznanie innego języka programowania używane w AI. Istnieje kilka języków programowania używanych w AI, co daje naukowcom i programistom możliwość wyboru najbardziej odpowiedniego, zgodnie z ich wymaganiami. Wszystkie te języki programowania zapewniają pewne wsparcie, takie jak intensywne biblioteki do obsługi sztucznej inteligencji. Różne języki programowania mają swoje zalety i wady. Java i Python są bardzo popularne, ale są powolne w wykonaniu i mogą nie być odpowiednie do tworzenia aplikacji współdziałających w krytycznym scenariuszu czasu rzeczywistego. C++ jest bardzo szybki, ale problem polega na tym, że nie nadaje się do wielozadaniowości. Tak więc C++ jest preferowany do napisania rdzenia aplikacji. R i Prolog to bardzo obiecujące języki, ale programistom, zwłaszcza początkującym, trudno się w nich rozwijać ze względu na inną składnię. Język może być odpowiedni dla jednego konkretnego typu projektu, ale nie dla innych.
Problem asocjacji danych był pierwotnie badany w kontekście śledzenia radarowego wielu celów, gdzie odbite impulsy są wykrywane w stałych odstępach czasu przez obracającą się antenę radaru. W każdym kroku czasowym na ekranie może pojawić się wiele impulsów, ale nie ma bezpośredniej obserwacji, które impulsy w czasie t odpowiadają którym impulsom w czasie t -1. Rysunek 18.8(a) pokazuje prosty przykład z dwoma skokami na krok czasowy dla pięciu kroków. Każdy impuls jest oznaczony swoim krokiem czasowym, ale nie zawiera żadnych informacji identyfikujących. Załóżmy na razie, że wiemy, że dokładnie dwa samoloty, A1 i A2, generują impulsy. W terminologii OUPM, A1 i A2 są gwarantowanymi obiektami, co oznacza, że gwarantuje się ich istnienie i odrębność; ponadto w tym przypadku nie ma innych obiektów. (Innymi słowy, jeśli chodzi o samoloty, ten scenariusz jest zgodny z semantyką bazy danych założoną w obrotach na minutę.) Niech ich prawdziwe pozycje to X(A1, t) i X(A2, t), gdzie t jest nieujemną liczbą całkowitą indeksuje czasy aktualizacji czujnika. Zakładamy, że pierwsza obserwacja dociera do t=1, a w czasie 0 wcześniejszy rozkład dla lokalizacji każdego samolotu to InitX(). Aby uprościć sprawę, założymy również, że każdy samolot porusza się niezależnie, zgodnie ze znanym modelem przejściowym – np. liniowym – modelem gaussowskim używanym w filtrze Kalmana. Ostatnim elementem jest model czujnika: ponownie zakładamy model liniowo – gaussowski, w którym samolot w pozycji x wytwarza blip b, którego obserwowana pozycja blipu Z(b) jest liniową funkcją x z dodanym szumem gaussowskim. Każdy samolot generuje dokładnie jeden impuls w każdym kroku czasowym, więc impuls ma za początek samolot i krok czasowy. Tak więc, pomijając na razie poprzedni, model wygląda tak:
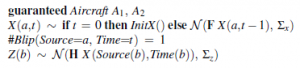
gdzie F i Σx są macierzami opisującymi model przejścia liniowego i kowariancją szumu przejścia, a H i Σz są odpowiednimi macierzami dla modelu czujnika. Kluczową różnicą między tym modelem a standardowym filtrem Kalmana jest to, że istnieją dwa obiekty generujące odczyty czujnika (blips). Oznacza to, że w danym kroku czasowym istnieje niepewność co do tego, który obiekt wytworzył dany odczyt czujnika. Każdy możliwy świat w tym modelu zawiera asocjację – zdefiniowaną przez wartości wszystkich zmiennych Source(b) dla wszystkich kroków czasowych – między samolotem a impulsami. Dwie możliwe hipotezy asocjacyjne przedstawiono na rysunku (b–c).
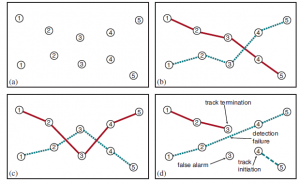
Ogólnie rzecz biorąc, dla n obiektów i T przedziałów czasowych istnieje (n!)T sposobów przypisywania impulsów do samolotów – strasznie duża liczba. Opisany dotychczas scenariusz obejmował n znanych obiektów generujących n obserwacji w każdym kroku czasowym. Rzeczywiste zastosowania asocjacji danych są zazwyczaj znacznie bardziej skomplikowane. Często zgłaszane obserwacje zawierają fałszywe alarmy (znane również jako bałagan), które nie są spowodowane przez rzeczywiste obiekty. Mogą wystąpić błędy wykrywania, co oznacza, że nie zostanie zgłoszona żadna obserwacja Bałagan dla rzeczywistego obiektu. W końcu pojawiają się nowe obiekty, a stare znikają. Zjawiska te, które tworzą jeszcze więcej możliwych światów, o które można się martwić, zostały zilustrowane na rysunku (d). Odpowiednia jednostka OUPM jest pokazana na rysunku
Ze względu na jego praktyczne znaczenie zarówno dla zastosowań cywilnych, jak i wojskowych, napisano dziesiątki tysięcy artykułów na temat problemu śledzenia wielu celów i kojarzenia danych. Wielu z nich po prostu próbuje opracować złożone matematyczne szczegóły obliczeń prawdopodobieństwa dla modelu z rysunku 18.9 lub dla jego prostszych wersji. W pewnym sensie jest to niepotrzebne, gdy model jest wyrażony w probabilistycznym języku programowania, ponieważ silnik wnioskowania ogólnego przeznaczenia wykonuje wszystkie obliczenia matematyczne poprawnie dla dowolnego modelu – w tym tego. Co więcej, opracowanie scenariusza (latanie formacji, obiekty zmierzające do nieznanych miejsc docelowych, obiekty startujące lub lądujące itp.) mogą być obsługiwane przez niewielkie zmiany w modelu bez uciekania się do nowych wyprowadzeń matematycznych i skomplikowanego programowania. Z praktycznego punktu widzenia wyzwaniem z tego rodzaju modelem jest złożoność wnioskowania. Podobnie jak w przypadku wszystkich modeli prawdopodobieństwa, wnioskowanie oznacza sumowanie zmiennych innych niż zapytanie i dowody. Do filtrowania w HMM i DBN byliśmy w stanie zsumować zmienne stanu od 1 do t-1 za pomocą prostej sztuczki programowania dynamicznego; w przypadku filtrów Kalmana wykorzystaliśmy również specjalne właściwości Gaussa. Jeśli chodzi o powiązanie danych, mamy mniej szczęścia. Nie ma (znanego) wydajnego dokładnego algorytmu, z tego samego powodu, dla którego nie ma żadnego dla przełączania filtru Kalmana: rozkład filtrowania, który opisuje łączny rozkład liczby i lokalizacji samolotów na każdym kroku czasowym, kończy się jako mieszanina wykładniczo wiele rozkładów, po jednym dla każdego sposobu wybierania sekwencji obserwacji do przypisania do każdego statku powietrznego. W odpowiedzi na złożoność wnioskowania dokładnego zastosowano kilka metod przybliżonych. Najprostszym podejściem jest wybranie jednego „najlepszego” przypisania w każdym kroku czasowym, biorąc pod uwagę przewidywane pozycje obiektów w bieżącym czasie. To przypisanie wiąże obserwacje z obiektami i umożliwia aktualizację śladu każdego obiektu oraz wykonanie prognozy dla następnego kroku czasowego. Do wyboru „najlepszego” przypisania często stosuje się tak zwany filtr najbliższego sąsiada, który wielokrotnie wybiera najbliższą parę przewidywanej pozycji lter i obserwacji i dodaje tę parę do przypisania. Filtr najbliższego sąsiedztwa działa dobrze, gdy obiekty są dobrze rozdzielone w przestrzeni stanów, a niepewność predykcji i błąd obserwacji są małe – innymi słowy, gdy nie ma możliwości pomyłki. Gdy istnieje większa niepewność co do prawidłowego przypisania, lepszym podejściem jest wybór przypisania, które maksymalizuje łączne prawdopodobieństwo bieżących obserwacji, biorąc pod uwagę przewidywane pozycje. Można to zrobić wydajnie za pomocą algorytmu węgierskiego (Kuhn, 1955), mimo że jest n! zadania do wyboru, gdy nadejdzie każdy nowy przedział czasowy. Każda metoda, która zobowiązuje do jednego najlepszego przypisania w każdym kroku czasowym, sromotnie zawodzi w trudniejszych warunkach. W szczególności, jeśli algorytm dokona nieprawidłowego przypisania, przewidywanie w następnym kroku czasowym może być znacząco błędne, prowadząc do większej liczby nieprawidłowych przypisań i tak dalej. Podejścia do próbkowania mogą być znacznie bardziej efektywne. Algorytm filtrowania cząstek do powiązania danych działa poprzez utrzymywanie dużego zbioru możliwych bieżących przypisań. Algorytm MCMC bada przestrzeń historii przypisania — na przykład rysunek (b–c) może być stanami w przestrzeni stanów MCMC — i może zmienić zdanie na temat poprzednich decyzji przypisania. Jednym z oczywistych sposobów na przyspieszenie wnioskowania opartego na próbkowaniu dla śledzenia wielocelowego jest użycie sztuczki Rao-Blackwellization z rozdziału 14 (strona 514): biorąc pod uwagę konkretną hipotezę asocjacji dla wszystkich obiektów, obliczenia filtrowania dla każdego obiektu można zazwyczaj wykonać dokładnie i wydajnie, zamiast próbkowania wielu możliwych sekwencji stanów dla obiektów. Na przykład w modelu z rysunku 18.9 obliczenia filtrowania oznaczają po prostu uruchomienie filtru Kalmana dla sekwencji obserwacji przypisanych do danego hipotetycznego obiektu. Co więcej, przy przejściu z jednej hipotezy asocjacyjnej na inną, obliczenia muszą być powtórzone tylko dla obiektów, których skojarzone obserwacje uległy zmianie. Obecne metody asocjacji danych MCMC mogą obsługiwać wiele setek obiektów w czasie rzeczywistym, dając jednocześnie dobre przybliżenie prawdziwych rozkładów a posteriori.
R został opracowany w 1995 roku przez Rossa Ihakę i Roberta Gentlemana w celu ułatwienia statystyki i analizy danych. R jest preferowany do programowania AI, ponieważ jest bardzo wydajny w radzeniu sobie z dużymi wartościami liczbowymi. Również R obsługuje różne właściwości programowania, takie jak obliczenia wektorowe i programowanie obiektowe. R zapewnia szeroką gamę pakietów i funkcji wspierających programowanie AI. Zapewnia dobre możliwości współpracy z innymi głównymi językami programowania, takimi jak C, C++ i Fortan. Posiada możliwość tworzenia wykresów dobrej jakości. Popularne pakiety w R to:
Ponadto R ma bardzo aktywne i silne wsparcie społeczności. Wszystko to sprawia, że R nadaje się do tworzenia aplikacji AI. Główną wadą R jest to, że używa więcej pamięci w porównaniu do innych języków programowania, takich jak Python. Brakuje mu podstawowych zabezpieczeń, przez co nie nadaje się do aplikacji internetowych. Osoby bez znajomości języka programowania mają trudności z nauką R. Trudno jest wdrożyć algorytmy przez początkujących. Nie nadaje się do grafiki i jest znacznie wolniejszy w wykonaniu.
Wcześniej rozważaliśmy problem śledzenia stanu świata, ale obejmowliśmy tylko przypadek reprezentacji atomowych (HMM) i reprezentacji czynnikowych (DBN i filtry Kalmana). Ma to sens w przypadku światów z jednym obiektem – być może pojedynczym pacjentem na oddziale intensywnej terapii lub pojedynczym ptakiem przelatującym przez las. W tej sekcji zobaczymy, co się dzieje, gdy dwa lub więcej obiektów generuje obserwacje. Tym, co odróżnia ten przypadek od zwykłej starej oceny stanu, jest to, że istnieje teraz możliwość niepewności co do tego, który obiekt wygenerował jaką obserwację. Jest to problem niepewności tożsamości, o którym mowa w rozdziale 18.2 (strona 648), obecnie rozpatrywany w kontekście czasowym. W literaturze dotyczącej teorii sterowania jest to problem asocjacji danych — to znaczy problem asocjacji danych obserwacyjnych z obiektami, które je wygenerowały. Chociaż moglibyśmy postrzegać to jako kolejny przykład modelowania probabilistycznego otwartego wszechświata, w praktyce jest ono na tyle ważne, że zasługuje na osobną sekcję.