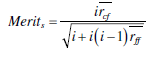Miesiąc: sierpień 2022

Badania przeprowadzono na stacji roboczej Intel (R) Xeon 2X10 Cores E5-2480v2@3,20 GHz/48 GB RAM z kartą graficzną NVIDIA P400 8 GB. Do oceny wyników klasyfikacji wykorzystano czas modelu uczącego (t_trg), precyzję (P), statystykę Kappa (K ), ogólną dokładność (OA) i charakterystykę operacyjną odbiornika (ROC). Te same zestawy parametrów wykorzystano również do optymalizacji parametrów modelu RF.

Zbadaliśmy ekspresyjne reprezentacje modeli prawdopodobieństwa opartych zarówno na logice, jak i programach.

• Modele prawdopodobieństwa relacyjnego (RPM) definiują modele prawdopodobieństwa na światach wyprowadzone z semantyki baz danych dla języków pierwszego rzędu; są właściwe, gdy wszystkie przedmioty i ich tożsamości są znane z całą pewnością.
• Biorąc pod uwagę RPM, obiekty w każdym możliwym świecie odpowiadają stałym symbolom w RPM, a podstawowe zmienne losowe są wszystkimi możliwymi wystąpieniami symboli predykatów z obiektami zastępującymi każdy argument. Zatem zbiór światów możliwych jest skończony.
• RPM dostarczają bardzo zwięzłe modele dla światów z dużą liczbą obiektów i mogą poradzić sobie z relacyjną niepewnością.
• Modele prawdopodobieństwa otwartego wszechświata (OUPM) opierają się na pełnej semantyce logiki pierwszego rzędu, pozwalając na nowe rodzaje niepewności, takie jak niepewność tożsamości i istnienia.
• Programy generatywne to reprezentacje modeli prawdopodobieństwa – w tym OUPM – jako programy wykonywalne w probabilistycznym języku programowania lub PPL. Program generatywny reprezentuje rozkład śladów wykonania programu. PPL zazwyczaj zapewniają uniwersalną moc ekspresji dla modeli prawdopodobieństwa.

W tym eksperymencie klasyfikator RF jest optymalizowany za pomocą dwóch parametrów: (i) liczby losowych drzew do zbudowania RF oraz (ii) liczby optymalnych zestawów danych funkcji do RF. RF charakteryzuje się zasadami pakowania i losowego wyboru najlepszej cechy. Jest to jeden z najbardziej dominujących klasyfikatorów zespołowych do klasyfikacji obrazów RS. RF jest zbudowany ze zbioru klasyfikatorów o strukturze drzewa {h(x, Θr), r = 1…R}, gdzie Θ_r  są identycznie rozłożonymi niezależnymi klasyfikatorami drzewa losowego, a każdy klasyfikator drzewa oddaje głos jednostkowy za ostateczną klasyfikację danych wejściowych x. Tutaj rozmiar jądra RF, który reprezentuje liczbę Θr, jest reprezentowany przez R. Algorytm klasyfikacji RF można zilustrować w następujący sposób:

ALGORYTM DLA RF

1. Dla r = 1 do R;
2. a) Narysuj próbkę treningową przez bootstrap Z* o rozmiarze N z T_S
3. b) Rozwijaj h(x, Θ_r) do próbek bootstrapowych, powtarzając kolejne kroki dla każdego węzła Θ_r aż do osiągnięcia minimalnego rozmiaru węzła
4. Wybierz losowo m funkcji z funkcji S (m ≪ S)
5. Wybierz najlepszą cechę spośród m

iii. Podziel węzeł

2. Wyprowadź zespół drzew

3. Dokonać prognozy klasyfikacyjnej w nowym punkcie x; jeśli jest predykcją klasy r-tego drzewa  = głosowanie większością 

Po skonstruowaniu zespołu h(x, Θ_r) o rozmiarze R, głosowanie większościowe dla przewidywania klasy

r_thRF może być wykonane poprzez agregację końcowej klasy każdego drzewa i odpowiadających jej głosów ważonych. Każde drzewo jest uprawiane w jak największym stopniu bez żadnego przycinania. W każdym zestawie treningowym bootstrap około jednej trzeciej instancji szkoleniowych pozostaje do oszacowania błędu RF. Nazywa się to danymi out-of-bag i nie jest używane do budowy r-tego drzewa losowego. Nazywa się to również błędem worka w zestawie danych uczących, który przewiduje błąd testu podczas budowy RF bez użycia mechanizmu walidacji krzyżowej. Służy również do sprawdzania trafności funkcji w losowo wybranej funkcji. Następnie RF jest kalibrowany z odpowiednim rozmiarem zespołu (R) i liczbą cech (m) w celu optymalizacji modelu w celu uzyskania wyższej wydajności pod względem dokładności klasyfikacji i złożoności obliczeniowej. Kalibrację parametrów modelu RF przeprowadza się w sposób przedstawiony poniżej:

1. RF został zainicjowany z R = 5 z przyrostem co 5, maksymalnie do 200 lub do osiągnięcia najwyższej wydajności.
2. Wartość R została określona jako otrzymana z największą dokładnością wcześniejszej oceny.

iii. Podobnie jak we wcześniejszym teście, RF jest inicjowany z m = 1 i wykonywany z przyrostem od 1 do m = 147 dla T_F i m = 9 dla T_S.

1. W każdym wykonaniu model RF może wybrać najlepsze cechy predykcyjne poprzez losowy wybór cech podczas każdego podziału węzła
2. Wartość m jest ustawiana na te wartości, od których otrzymana dokładność była najwyższa.
3. Ostatecznie R i 𝑚 są kalibrowane zoptymalizowanymi wartościami otrzymanymi z poprzednich eksperymentów, dla których uzyskano najwyższą dokładność klasyfikacji.

Podobnie jak w przypadku OUPM, dokładne wnioskowanie w programach generatywnych jest zwykle zbyt drogie lub niemożliwe. Z drugiej strony łatwo jest zobaczyć, jak wykonać próbkowanie odrzuceń: uruchom program, zachowaj tylko ślady zgodne z dowodami i policz różne odpowiedzi na zapytania znalezione w tych śladach. Ważenie prawdopodobieństwa jest również proste: dla każdego wygenerowanego śladu śledź wagę śladu, mnożąc wszystkie prawdopodobieństwa wartości obserwowanych po drodze. Ważenie prawdopodobieństwa działa dobrze tylko wtedy, gdy dane są dość prawdopodobne zgodnie z modelem. W trudniejszych przypadkach MCMC jest zwykle metodą z wyboru. MCMC stosowane do programów probabilistycznych polega na próbkowaniu i modyfikowaniu śladów wykonania. Wiele rozważań wynikających z OUPM ma również zastosowanie w tym przypadku; ponadto algorytm musi uważać na modyfikacje śladu wykonania, takie jak zmiana wyniku instrukcji if, która może unieważnić pozostałą część śladu. Dalsze ulepszenia wnioskowania pochodzą z kilku linii pracy. Niektóre ulepszenia mogą spowodować fundamentalne zmiany w klasie problemów, które można rozwiązać za pomocą danego PPL, nawet co do zasady; wnioskowanie zniesione, opisane wcześniej dla RPM, może mieć taki efekt. W wielu przypadkach ogólne MCMC jest zbyt wolne i potrzebne są propozycje specjalnego przeznaczenia, aby umożliwić szybkie mieszanie procesu wnioskowania. Ważnym celem ostatnich prac nad PPL było ułatwienie użytkownikom definiowania i używania takich propozycji, tak aby wydajność wnioskowania PPL była zgodna z niestandardowymi algorytmami wnioskowania opracowanymi dla określonych modeli. Wiele obiecujących podejść ma na celu zmniejszenie kosztów wnioskowania probabilistycznego. Pomysł kompilacji opisany dla sieci Bayesa w sekcji 13.4.3 można zastosować do wnioskowania w jednostkach OUPM i PPL i zazwyczaj daje przyśpieszenia od dwóch do trzech rzędów wielkości. Pojawiły się również propozycje sprzętu specjalnego przeznaczenia dla algorytmów, takich jak przekazywanie wiadomości i MCMC. Na przykład sprzęt Monte Carlo wykorzystuje małoprecyzyjne reprezentacje prawdopodobieństwa i masową, drobnoziarnistą równoległość, aby zapewnić 100–10 000 razy większą szybkość i wydajność energetyczną. Metody oparte na uczeniu się mogą również dać znaczną poprawę szybkości. Na przykład adaptacyjne dystrybucje propozycji mogą stopniowo uczyć się, jak generować propozycje MCMC, które z rozsądnym prawdopodobieństwem zostaną zaakceptowane i będą wystarczająco skuteczne w badaniu krajobrazu prawdopodobieństwa modelu, aby zapewnić szybkie mieszanie. Możliwe jest również trenowanie modeli uczenia głębokiego w celu reprezentowania rozkładów propozycji dla próbkowania ważności przy użyciu danych syntetycznych, które zostały wygenerowane na podstawie modelu bazowego. Ogólnie rzecz biorąc, oczekuje się, że jakikolwiek formalizm zbudowany na bazie ogólnych języków programowania napotka barierę obliczalności, i tak jest w przypadku PPL. Jeśli jednak założymy, że program bazowy zatrzymuje się dla wszystkich danych wejściowych i wszystkich losowych wyborów, czy dodatkowy wymóg wnioskowania probabilistycznego nadal sprawia, że ​​problem jest nierozstrzygnięty? Okazuje się, że odpowiedź brzmi tak, ale tylko dla modelu obliczeniowego z ciągłymi zmiennymi losowymi o nieskończonej precyzji. W takim przypadku staje się możliwe napisanie obliczalnego modelu prawdopodobieństwa, w którym wnioskowanie koduje problem zatrzymania. Z drugiej strony, w przypadku liczb o skończonej precyzji i gładkich rozkładów prawdopodobieństwa zwykle używanych w rzeczywistych aplikacjach, wnioskowanie pozostaje rozstrzygalne.

Próbki pokrycia terenu oparte na faktach gruntowych charakteryzują się zestawem atrybutów lub cech, za pomocą których można zidentyfikować i oddzielić wzór klas pokrycia terenu. Dobór cech do jednoznacznej identyfikacji klas pokrycia terenu w przestrzeni cech jest kluczowy nie tylko dla poprawy dokładności klasyfikacji; wybór odpowiedniej cechy może zminimalizować złożoność obliczeniową. Cechy w danych RS są głównie związane z właściwościami przestrzenno-spektralnymi. Opakowania i filtry są szeroko stosowane jako techniki wyboru funkcji w większości aplikacji ML. Częściej stosowane są techniki wyboru cech oparte na filtrach, ponieważ są wydajne obliczeniowo i mogą obsługiwać duże zbiory danych cech. Do badania przyjęliśmy technikę selekcji cech opartą na korelacji (CFS), która została skutecznie wykorzystana w aplikacjach RS w celu zwiększenia wydajności technik ML. CFS generuje podzbiory cech, niezależnie od modelu klasyfikacji i charakteryzuje się wydajną złożonością obliczeniową. Zasadą CFS jest filtr, w którym istotność optymalnego zestawu cech jest identyfikowana poprzez obserwację odpowiedniej miary korelacji. Niech F będzie zbiorem cech oryginalnych danych treningowych przed zastosowaniem CFS. Cecha f_r ∈ F jest traktowana jako istotna, jeśli istnieje jakaś cecha f_i ∈ F do orzekania klasy będącej przedmiotem zainteresowania c, dla której p(f_r = f_i) > 0 takie, że

gdzie c jest współczynnikiem korelacji Pearsona dla każdego obliczenia wzajemnej korelacji cecha-cecha i cecha-klasa (C). Podzbiór cech, który zawiera cechy z cechami nieskorelowanymi z cechami cech, ale jest silnie skorelowany z cechą do zdolności predykcyjnych klasy, nazywany jest optymalnym podzbiorem cech. Jeżeli zdefiniowana jest średnia korelacja między cechami a klasą  i podana jest średnia interkorelacja między każdą parą cech  to Merit_s” podzbioru S ∈ F z cechami i można obliczyć jako :

Istotność cechy lub podzbioru cech będzie oparta na stopniu, w jakim identyfikuje klasy w przestrzeni instancji cech, które nie zostały jeszcze zidentyfikowane przez inne cechy; to jest reprezentowane przez Merit_s Algorytm CFS oblicza i dla każdego S ∈ F i wyszukuje następny podzbiór funkcji w kierunku do przodu przy użyciu najlepszego pierwszego algorytmu wyszukiwania, wprowadzając lokalne zmiany w bieżącej funkcji. Wyszukiwanie do przodu zatrzymuje się po pięciu kolejnych w pełni rozwiniętych węzłach, które nie wykazują wzrostu Merits. Podzbiór cech o najwyższej Meritum traktowany jest jako optymalny podzbiór cech i służy do definiowania każdej z klas pokrycia terenu. Następnie uczący zestaw danych zdefiniowany przez optymalny zestaw cech jest oceniany przy użyciu algorytmu klasyfikacji C4.5 przed uczeniem proponowanego klasyfikatora opartego na ML. Uczący zbiór danych z oryginalnym zestawem cech i uczący zbiór danych z optymalnym podzbiorem cech są reprezentowane odpowiednio jako TF i TS. Dla zbioru danych ROSIS-3, wszystkie cechy F=147 zostały ocenione w celu uzyskania optymalnego podzbioru zbioru cech zdefiniowanego przez S=9. Szczegółowa obserwacja eksperymentalna dotycząca wyboru cech jest zilustrowana w sekcji „Wyniki i dyskusja”. Klasyfikator RF zostanie przeszkolony z użyciem zestawów danych TF i TS, aby ocenić, czy klasyfikator RF wytrenowany z optymalnym podzbiorem funkcji poprawił ogólną wydajność klasyfikatora RF.

Probabilistyczne języki programowania są modułowe w sposób ułatwiający eksplorowanie ulepszeń modelu bazowego. Rysunek 18.15 przedstawia program generatywny dla ulepszonego modelu, który generuje litery sekwencyjnie, a nie niezależnie.

Ten program generatywny wykorzystuje model Markowa, który rysuje każdą literę podaną w poprzedniej literze, z prawdopodobieństwem przejścia oszacowanym na podstawie listy referencyjnej słów angielskich. Rysunek przedstawia dwanaście próbkowanych obrazów wytworzonych przez ten generatywny program. Zauważ, że sekwencje liter są znacznie bardziej podobne do angielskiego niż te wygenerowane z programu na rysunku. Panel po prawej stronie na rysunku pokazuje wyniki wnioskowania z tego modelu Markowa zastosowanego do obrazu o wysokim poziomie szumów. Interpretacje bardziej pasują do generowania śladu, choć nadal istnieje pewna niepewność.

Usunięcie zbędnych pasm lub redukcja wymiarów pasm widmowych jest najważniejszą wadą teledetekcji hiperspektralnej, gdy wykorzystywane są konwencjonalne techniki przetwarzania obrazu. Minimalny udział szumów (MNF) i analiza składowych niezależnych (ICA) należą do tej samej rodziny analizy składowych (PCA). Zarówno MNF, jak i ICA są dominującymi technikami redukcji wymiarów stosowanymi w hiperspektralnych zastosowaniach RS. Stwierdzono, że MNF jest bardzo skuteczny w redukcji hiperspektralnego pasma widmowego. Wymaga wcześniejszych ocen macierzy kowariancji sygnału i szumu oraz wymaga większych zasobów obliczeniowych niż PCA. Ma jednak przewagę nad PCA, ponieważ uwzględnia informacje o szumie w domenie przestrzennej. Z drugiej strony ICA jest kosztowna obliczeniowo, co ogranicza jej zastosowanie. W obecnym badaniu MNF został wykorzystany do redukcji wymiarowości zbioru danych ROSIS-3. Transformacja MNF została wykonana poprzez dwie kolejne transformacje PCA. Pierwszy PCA wykorzystuje komputery PC macierzy kowariancji szumu do dekorelacji i przeskalowania pikseli (zaszumionych) w obrazie. Wewnętrzna wymiarowość obrazu jest wybierana na podstawie końcowych wartości własnych i powiązanych obrazów uzyskanych przy użyciu komputerów PC. Wybierane są pasma o wyższych wartościach własnych, ponieważ obrazy o wartościach własnych bliższych 1 to głównie szum. Widmowy wymiar oryginalnego obrazu z 103 pasmami pozostaje tylko z 27 pasmami po procesie redukcji wymiarów.

Zastosujmy ten model do interpretacji obrazów liter, które zostały zdegradowane za pomocą szumu addytywnego. Rysunek przedstawia obraz zdegradowany wraz z wynikami z trzech niezależnych przebiegów MCMC.

Dla każdego przebiegu pokazujemy renderowanie liter zawartych w śladzie po zatrzymaniu łańcucha Markowa. We wszystkich trzech przypadkach wynikiem jest niepewność sekwencji liter, co sugeruje, że rozkład a posteriori jest silnie skoncentrowany na prawidłowej interpretacji.

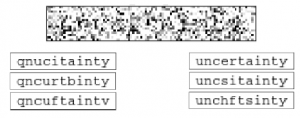
Teraz zdegradujmy tekst jeszcze bardziej, zamazując go na tyle, że trudno go przeczytać. Rysunek przedstawia wyniki wnioskowania na tym trudniejszym wejściu.

Tym razem, chociaż wydaje się, że wnioskowanie MCMC zbiegło się na (jak wiemy) prawidłowej liczbie liter, pierwsza litera jest błędnie identyfikowana jako q i nie ma pewności co do pięciu z dziesięciu kolejnych liter. W tym momencie istnieje wiele możliwych sposobów interpretacji wyników. Możliwe, że wnioskowanie MCMC dobrze się wymieszało, a wyniki są dobrym odzwierciedleniem prawdziwego a posteriori, biorąc pod uwagę model i obraz; w takim przypadku niepewność niektórych liter i błąd w pierwszej literze są nieuniknione. Aby uzyskać lepsze wyniki, może być konieczne ulepszenie modelu tekstowego lub zmniejszenie poziomu szumu. Możliwe też, że wnioskowanie MCMC nie zostało prawidłowo wymieszane: jeśli uruchomimy 300 łańcuchów dla 25 tysięcy lub 25 milionów iteracji, możemy znaleźć całkiem inny rozkład wyników, być może wskazujący, że pierwszą literą jest prawdopodobnie u, a nie q. Prowadzenie większej liczby wniosków może być kosztowne pod względem pieniędzy i czasu oczekiwania. Co więcej, nie ma niezawodnego testu na zbieżność metod wnioskowania Monte Carlo. Moglibyśmy spróbować ulepszyć algorytm wnioskowania, być może projektując lepszy rozkład propozycji dla MCMC lub używając wskazówek oddolnych z obrazu, aby sugerować lepsze początkowe hipotezy. Te ulepszenia wymagają dodatkowego przemyślenia, implementacji i debugowania. Trzecią alternatywą jest ulepszenie modelu. Na przykład moglibyśmy włączyć wiedzę o angielskich słowach, taką jak prawdopodobieństwa par liter. Rozważamy teraz tę opcję.

W badaniach wykorzystano 103 skorygowane atmosferycznie kanały spektralne ROSIS-3 o zakresie spektralnym 0,43–0,86 μm z rozdzielczością przestrzenną 1,3 m. Informacje o próbach treningowo-testowych klas dla zbioru danych Uniwersytetu w Pawii w północnych Włoszech przedstawiono w Tabeli

Zestaw danych Pavia został uprzejmie dostarczony przez prof. Paolo Gamba. Obraz kompozytowy w fałszywych kolorach (FCC) badanego obszaru i rozkład próbek treningowych przedstawiono na rysunku

Program generatywny to program wykonywalny, w którym każdy losowy wybór definiuje zmienną losową w powiązanym modelu prawdopodobieństwa. Wyobraźmy sobie, że krok po kroku rozwijamy wykonanie programu dokonującego losowych wyborów. Niech X_i będzie zmienną losową odpowiadającą i-temu losowemu wyborowi dokonanemu przez program; jak zwykle x_i oznacza możliwą wartość X_i. Wywołajmy ω = {x_i} ślad wykonania programu generatywnego – czyli sekwencja możliwych wartości dla losowych wyborów. Jednokrotne uruchomienie programu generuje jeden taki ślad, stąd określenie „program generatywny”. Przestrzeń wszystkich możliwych śladów wykonania Ω można postrzegać jako przestrzeń próbki modelu prawdopodobieństwa zdefiniowanego przez program generatywny. Rozkład prawdopodobieństwa po śladach można zdefiniować jako iloczyn prawdopodobieństw każdego indywidualnego losowego wyboru: P(ω) = Π_iP(x_i|x₁,…,x_i-1). Jest to analogiczne do dystrybucji na światy w OUPM. Koncepcyjnie proste jest przekształcenie dowolnego OUPM w odpowiedni program generatywny. Ten program generatywny dokonuje losowych wyborów dla każdego wyrażenia liczbowego i dla wartości każdej podstawowej zmiennej losowej, której istnienie jest implikowane przez wyrażenia liczbowe. Główną dodatkową pracą, jaką musi wykonać program generatywny, jest utworzenie struktur danych, które reprezentują obiekty, funkcje i relacje możliwych światów w OUPM. Te struktury danych są tworzone automatycznie przez silnik wnioskowania OUPM, ponieważ OUPM zakłada, że ​​każdy możliwy świat jest strukturą modelu pierwszego rzędu, podczas gdy typowy PPL nie przyjmuje takiego założenia. Obrazy na rysunku można wykorzystać do intuicyjnego zrozumienia rozkładu prawdopodobieństwa P(Ω): widzimy różne poziomy szumu, a na mniej zaszumionych obrazach widzimy również sekwencje liter o różnej długości.

Niech ω₁ będzie śladem odpowiadającym obrazowi w prawym górnym rogu tej figury, zawierającym litery ocflwe. Gdybyśmy rozwinęli ten ślad ω₁ do sieci bayesowskiej, miałby 4104 węzłów: 1 węzeł dla zmiennej n; 6 węzłów dla zmiennych letters[i]; 1 węzeł dla wariancji szumu; i 4096 węzłów dla pikseli w zaszumionym obrazie. Widzimy zatem, że ten program generatywny definiuje model prawdopodobieństwa otwartego wszechświata: liczba dokonywanych przez niego losowych wyborów nie jest ograniczona a priori, lecz zależy od wartości zmiennej losowej n.