Przypomnijmy, że model prawdopodobieństwa definiuje zbiór W możliwych światów o prawdopodobieństwie P(ω) dla każdego świata ω. W przypadku sieci bayesowskich możliwe światy to przypisania wartości do zmiennych; w szczególności w przypadku Boole’a możliwe są światy: identyczne z logiką zdań. W przypadku modelu prawdopodobieństwa pierwszego rzędu wydaje się zatem, że potrzebujemy możliwych światów logiki pierwszego rzędu, to znaczy zbioru obiektów z relacjami między nimi i interpretacji, która odwzorowuje stałe symbole na obiekty, predykaty symboli do relacje i symbole funkcyjne do funkcji na tych obiektach. Model musi również zdefiniować prawdopodobieństwo dla każdego takiego możliwego świata, tak jak sieć bayesowska definiuje prawdopodobieństwo dla każdego przypisania wartości do zmiennych. Załóżmy na chwilę, że wymyśliliśmy, jak to zrobić. Następnie, jak zwykle, możemy otrzymać prawdopodobieństwo dowolnego zdania logicznego pierwszego rzędu φ (phi) jako sumę dla możliwych światów, w których jest prawdziwe:
![]()
Prawdopodobieństwa warunkowe P(φ|e) można otrzymać w podobny sposób, więc możemy w zasadzie zadać dowolne pytanie dotyczące naszego modelu – i uzyskać odpowiedź. Na razie w porządku. Jest jednak pewien problem: zbiór modeli pierwszego rzędu jest nieskończony. Widzimy to wyraźnie na rysunku (u góry). Oznacza to, że (1) sumowanie w równaniu (18.1) może być niewykonalne, oraz (2) określenie pełnego, spójnego rozkładu na nieskończony zbiór światów może być bardzo trudne.
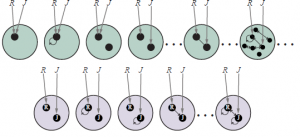
W tej sekcji unikamy tego problemu, biorąc pod uwagę semantykę bazy danych zdefiniowaną wcześniej. Semantyka bazy danych zakłada założenie unikalnych nazw – tutaj przyjmujemy ją dla stałych symboli. Zakłada również zamknięcie domeny – nie ma więcej obiektów poza tymi, które są nazwane. Możemy wtedy zagwarantować skończony zbiór możliwych światów, czyniąc zbiór obiektów w każdym świecie dokładnie zbiorem stałych symboli, które są używane; jak pokazano na rysunku (na dole), nie ma niepewności co do mapowania symboli na obiekty lub co do istniejących obiektów. Modele zdefiniowane w ten sposób nazwiemy relacyjnymi modelami prawdopodobieństwa, czyli RPM.1 Najważniejszą różnicą między semantyką RPM a semantyką baz danych jest to, że RPM nie dokonują założenia o zamkniętym świecie – w probabilistycznym rozumowania nie możemy po prostu założyć, że każdy nieznany fakt jest fałszywy.