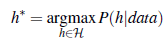Przetwarzanie obrazu to zbiór metod stosowanych do wykonywania niektórych technik na obrazie w celu uzyskania przydatnych informacji z obrazu lub wzmocnienia wizualnych wskazówek na obrazie w zakresie kolorów, kontrastów itp. Przetwarzanie obrazu to kategoria przetwarzania sygnału, w której obrazy są dane wejściowe i obrazy lub niektóre z powiązanych z nimi atrybutów są danymi wyjściowymi. Stanowi również ważny obszar badawczy w dziedzinie informatyki i dziedzin multidyscyplinarnych.
Drzewo decyzyjne to reprezentacja funkcji, która odwzorowuje wektor wartości atrybutów na pojedynczą wartość wyjściową — „decyzję”. Drzewo decyzyjne podejmuje decyzję, wykonując sekwencję testów, zaczynając od korzenia i podążając za odpowiednią gałęzią, aż do osiągnięcia liścia. Każdy węzeł wewnętrzny w drzewie odpowiada testowi wartości jednego z atrybutów wejściowych, gałęzie z węzła są oznaczone możliwymi wartościami atrybutu, a węzły liści określają, jaka wartość ma zostać zwrócona przez funkcję. Ogólnie rzecz biorąc, wartości wejściowe i wyjściowe mogą być dyskretne lub ciągłe, ale na razie rozważymy tylko dane wejściowe składające się z wartości dyskretnych i wartości wyjściowych, które są albo prawdziwe (przykład pozytywny), albo fałszywe (przykład negatywny). Nazywamy to klasyfikacją Boole’a. Użyjemy j do indeksowania przykładów (xj jest wektorem wejściowym dla j-tego przykładu, a yj jest wyjściem), a xj,i dla i-tego atrybutu j-tego przykładu. Drzewo reprezentujące funkcję decyzyjną używaną przez SR do problemu restauracji pokazano na rysunku.
Podążając za gałęziami widzimy, że przykład z Patrons=Full i WaitEstimate=0–10 zostanie sklasyfikowany jako pozytywny (tzn. tak, poczekamy na stolik)
W ciągu ostatnich lat sztuczna inteligencja (AI) doprowadziła do wielu innowacji i przełomu technologicznego w różnych obszarach automatyzacji. Sztuczna inteligencja ma na celu zautomatyzowanie systemów w celu uzyskania optymalnej wydajności i bardziej wydajnych wyników. Znajduje zastosowanie w wielu różnorodnych obszarach, takich jak diagnostyka dolegliwości u roślin lub zwierząt, wirtualne chatboty, zarządzanie żywym inwentarzem, samochody autonomiczne, analiza obrazu medycznego, łańcuch dostaw magazynowych, analiza aktywności sportowej, bezpieczeństwa, nadzoru itp. Pojemność komputerów, roboty lub każda maszyna do inteligentnej pracy nazywana jest sztuczną inteligencją. Tutaj maszyny lub komputery są wyposażone w cechy człowieka, np. rozumowanie i logikę, uogólnianie, uczenie się na podstawie doświadczenia itp. Celem AI można określić jako wykorzystanie pełnych możliwości pamięci i przetwarzania komputera w celu dopasowania do ludzkiego myślenia władzę w szerokim zakresie domen. Z biegiem lat opracowano techniki sztucznej inteligencji, aby ułatwić diagnostykę medyczną, wyszukiwarkę, nadzór wideo, bezpieczeństwo, rozpoznawanie obiektów itp. Różne takie techniki zostały wprowadzone w dziedzinie przetwarzania obrazu również w celu promowania, ułatwiania i optymalizacji różnych zastosowań w tej dziedzinie. Sposoby manipulowania obrazem w celu ulepszenia jego zawartości lub pobierania z niego informacji nazywa się przetwarzaniem obrazu. Znajduje zastosowanie w różnych aplikacjach, takich jak biometria, gry, egzekwowanie prawa i porządku, wizualizacja stanu zdrowia itp. Stosując sztuczną inteligencję do przetwarzania obrazu można wykonać wiele rodzajów rozwoju i czynności, takich jak wykrywanie obiektów, rozpoznawanie twarzy , przewidywanie chorób na podstawie obrazów, znajdowanie wzorców na obrazach lub wideo itp. Umożliwia to również nadzór wideo. Ten rozdział ma na celu zbadanie koncepcji sztucznej inteligencji w różnych dziedzinach przetwarzania obrazu. Druga część tego rozdziału wprowadza pojęcie przetwarzania obrazu; sztuczna inteligencja jest omówiona w trzeciej części; a następnie omówiono rolę AI w przetwarzaniu obrazu. Na koniec w tym wymieniono wyniki, dyskusję i wnioski w kolejnych sekcjach.
Szczegółowo opiszemy przykładowy problem uczenia nadzorowanego: problem z podjęciem decyzji, czy czekać na stolik w restauracji. Ten problem będzie używany w całym rozdziale, aby zademonstrować różne klasy modeli. W przypadku tego problemu wyjście, y, jest zmienną logiczną, którą nazwiemy WillWait; dotyczy to przykładów, w których czekamy na stolik. Wejście x jest wektorem dziesięciu wartości atrybutów, z których każda ma wartości dyskretne:
Zestaw 12 przykładów, zaczerpniętych z doświadczenia jednego z nas (SR), pokazano na rysunku
Zwróć uwagę, jak skąpe są te dane: jest 26 x 32 x 42 = 9,216 możliwych kombinacji wartości atrybutów wejściowych, ale otrzymujemy poprawne dane wyjściowe tylko dla 12 z nich; każde z pozostałych 9204 może być prawdziwe lub fałszywe; nie wiemy. To jest istota indukcji: musimy jak najlepiej zgadnąć te brakujące 9204 wartości wyjściowe, biorąc pod uwagę tylko dowody z 12 przykładów.
Postęp technologiczny w zakresie przetwarzania obrazu spowodował wzrost wymagań w wielu dziedzinach aplikacji. Znaczące ulepszenia nastąpiły w rozwoju nowych algorytmów i platform przetwarzania obrazu. Niedawny rozwój technologii czujników zrewolucjonizował dziedzinę zastosowań, która pośrednio wymaga opracowania bardziej wyrafinowanych technik przetwarzania obrazu. Ponadto dostępność czujników satelitarnych i konstelacja satelitów obserwujących Ziemię na całym świecie dała ogromne możliwości modelowania powierzchni Ziemi w celu efektywnego zarządzania zasobami naturalnymi i działań monitorujących. Technologia RS stała się niezbędnym i uniwersalnym narzędziem w konfiguracji rządowej, w tym w przemyśle. Dziedzina ta przyciągnęła w ciągu ostatnich dwóch dekad wiele uwagi badawczej w zakresie innowacji technik przetwarzania obrazu. Rosnąca dostępność obrazów bezzałogowych statków powietrznych (UAV) szeregów czasowych znacznie zwiększyła częstotliwość monitorowania i zarządzania aktywnością zasobów. UAV są bardzo skutecznie wykorzystywane do monitorowania terenu w czasie rzeczywistym, częstych przeglądów; mogą szybko rejestrować obrazy w podwyższonej jakości [55]. W ciągu ostatniej dekady rynek dronów kwitł z wykładniczym wzrostem we wszystkich zakresach zastosowań, szczególnie w branży budowlanej. Najważniejszym aspektem w radzeniu sobie z analizą wielomodelową, śledzeniem obiektów w bałaganie itp. stają się nowe techniki przetwarzania danych lub modernizacja konwencjonalnych technik teledetekcyjnych [56]. Wiele obszarów zastosowań kładzie nacisk na automatyzację i minimalną interakcję między ludźmi; Techniki oparte na sztucznej inteligencji/ML stają się coraz bardziej istotne w obecnym scenariuszu. Sztuczna inteligencja i ML są kluczowymi komponentami i głównymi czynnikami napędzającymi hiperautomatyzację wraz z innymi technologiami, takimi jak narzędzia do automatyzacji procesów robotycznych. Wykorzystanie AI/ML jest stopniowo coraz bardziej powiązane z Internetem rzeczy (IoT) dla różnych zastosowań. AI, ML i DL są już wykorzystywane do tworzenia urządzeń i usług IoT w inteligentniejszy i bezpieczniejszy sposób. W ostatnim czasie podejścia oparte na DL stają się coraz bardziej odpowiednie do analizowania obrazów VHR, ponieważ wydajność zasobów obliczeniowych uległa znacznemu zwiększeniu dzięki dodaniu jednostki przetwarzania graficznego (GPU). Wprowadzono inny wariant modeli DL do obsługi danych o charakterze big data w obszarach RS. Możliwości obrazowania wysokowymiarowego przyniosły nowe możliwości i wyzwania w rozwoju klasyfikacji RS, szczególnie w przypadku bardzo podobnych spektralnie klas pokrycia terenu RYSUNEK 4.2 Klasyfikacja obszaru uniwersytetu w Pawii (ze zbiorem danych szkoleniowych TS czujnika ROSIS-3) za pomocą zoptymalizowanego RF metoda klasyfikacji klasyfikatorów. charakteryzują się zbędnymi i nieistotnymi cechami. Studium przypadku przedstawione w rozdziale kładzie nacisk na klasyfikację obrazów hiperspektralnych VHR przy użyciu podejścia zespołowego opartego na ML. Obejmuje szereg etapów przetwarzania obrazu, w których redukcja wymiarów w przestrzeni spektralnej i cech odegrała kluczową rolę w poprawie dokładności klasyfikacji. Raportuje zoptymalizowany klasyfikator RF na podstawie losowego wyboru próbek treningowych i zestawu funkcji. Proces ten zwiększył różnorodność klasyfikatorów bazowych, co skutkuje znaczną poprawą ogólnej klasyfikacji zbioru danych hiperspektralnych ROSIS-3 w porównaniu z innymi badanymi tutaj zaawansowanymi klasyfikatorami.
Bardziej formalnie, zadaniem nadzorowanego uczenia się jest:
Mając zestaw uczący N przykładowych par wejście-wyjście
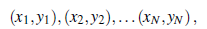
gdzie każda para została wygenerowana przez nieznaną funkcję y = f (x), odkrywa funkcję h, która przybliża prawdziwą funkcję f . Funkcja h nazywana jest hipotezą o świecie. Jest ona wyprowadzona z przestrzeni hipotez H możliwych funkcji. Na przykład przestrzeń hipotez może być zbiorem wielomianów stopnia 3; lub zestaw funkcji JavaScript; lub zestaw formuł logicznych 3-SAT Boolean. Za pomocą alternatywnego słownictwa możemy powiedzieć, że h jest modelem danych, narysowanym z klasy modelu H, lub możemy powiedzieć, że funkcją narysowaną z klasy funkcji. Wynik yi nazywamy podstawową prawdą – prawdziwą odpowiedzią, o którą prosimy nasz model. Jak wybieramy przestrzeń hipotezy? Możemy mieć wcześniejszą wiedzę na temat procesu, który wygenerował dane. Jeśli nie, możemy przeprowadzić eksploracyjną analizę danych: badanie danych za pomocą testów statystycznych i wizualizacji – histogramów, wykresów punktowych, wykresów skrzynkowych – aby poznać dane i uzyskać wgląd w to, jaka przestrzeń hipotez może być odpowiednia. Lub możemy po prostu wypróbować wiele przestrzeni hipotez i ocenić, która z nich działa najlepiej. Jak wybrać dobrą hipotezę z przestrzeni hipotez? Moglibyśmy mieć nadzieję na spójną hipotezę: h takie, że każdy xi w zbiorze uczącym ma h(xi) = yi. W przypadku wyjść o wartości ciągłej nie możemy oczekiwać dokładnego dopasowania do prawdy podstawowej; zamiast tego szukamy najlepiej dopasowanej funkcji, dla której każde h(xi) jest bliskie yi
Prawdziwą miarą hipotezy nie jest to, jak radzi sobie w zestawie uczącym, ale raczej to, jak dobrze radzi sobie z danymi wejściowymi, których jeszcze nie widziała. Możemy to ocenić za pomocą drugiej próbki par (xi,yi) zwanej zbiorem testowym. Mówimy, że h dobrze uogólnia, jeśli dokładnie przewiduje wyniki zbioru testowego.
Rysunek pokazuje, że funkcja h, którą odkrywa algorytm uczący się, zależy od przestrzeni hipotez H, którą bierze pod uwagę oraz od podanego zbioru uczącego.
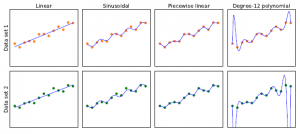
Każdy z czterech wykresów w górnym rzędzie ma ten sam zestaw uczący 13 punktów danych na płaszczyźnie (x,y). Cztery wykresy w dolnym rzędzie mają drugi zestaw 13 punktów danych; oba zbiory są reprezentatywne dla tej samej nieznanej funkcji f(x). Każda kolumna przedstawia najlepiej dopasowaną hipotezę h z innej przestrzeni hipotez:
Kolumna 1: Linie proste; funkcje postaci h(x) = w1x+w0. Nie ma linii, która byłaby spójną hipotezą dla punktów danych.
Kolumna 2: Funkcje sinusoidalne postaci h(x) = w1x+sin(w0x). Ten wybór nie jest do końca spójny, ale bardzo dobrze pasuje do obu zestawów danych.
Kolumna 3: Funkcje odcinkowo-liniowe, w których każdy segment linii łączy kropki z jednego punktu danych do następnego. Te funkcje są zawsze spójne.
Kolumna 4: Wielomiany 12 stopnia,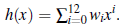 
Są one spójne: zawsze możemy uzyskać wielomian stopnia 12, aby idealnie dopasować 13 różnych punktów. Ale tylko dlatego, że hipoteza jest spójna, nie oznacza, że jest to dobre przypuszczenie. Jednym ze sposobów analizowania przestrzeni hipotez jest narzucane przez nie obciążenie (niezależnie od zestawu danych uczących) i wariancja, którą wytwarzają (z jednego zestawu uczącego do drugiego). Przez stronniczość rozumiemy (luźno) tendencję hipotezy predykcyjnej do odchylania się od wartości oczekiwanej po uśrednieniu dla różnych zestawów uczących. Bias często wynika z ograniczeń narzuconych przez przestrzeń hipotez.
Na przykład przestrzeń hipotez funkcji liniowych wywołuje silne obciążenie: dopuszcza jedynie funkcje składające się z linii prostych. Jeśli w danych występują jakiekolwiek wzorce inne niż ogólne nachylenie linii, funkcja liniowa nie będzie w stanie przedstawić tych wzorców. Mówimy, że hipoteza jest niedostateczna, gdy nie znajduje prawidłowości w danych. Z drugiej strony, odcinkowo funkcja liniowa ma niski błąd systematyczny; kształt funkcji zależy od danych. Przez wariancję rozumiemy wielkość zmiany hipotezy z powodu fluktuacji danych uczących. Dwa wiersze na rysunku 19.1 reprezentują zestawy danych, z których każdy był próbkowany z tej samej funkcji f(x). Zestawy danych okazały się nieco inne. W przypadku pierwszych trzech kolumn niewielka różnica w zestawie danych przekłada się na niewielką różnicę w hipotezie. Nazywamy to niską wariancją. Ale wielomiany stopnia 12 w czwartej kolumnie mają dużą wariancję: spójrz, jak różne są te dwie funkcje na obu końcach osi x. Oczywiście, co najmniej jeden z tych wielomianów musi być słabym przybliżeniem do prawdziwego f(x). Mówimy, że funkcja nadmiernie dopasowuje dane, gdy zwraca zbyt dużą uwagę na konkretny zestaw danych, na którym jest trenowana, co powoduje, że działa słabo na niewidocznych danych. Często występuje kompromis między obciążeniem a wariancją: wybór między bardziej złożonymi hipotezami o niskim odchyleniu, które dobrze pasują do danych uczących, a prostszymi hipotezami o niskiej wariancji, które mogą lepiej uogólniać. Albert Einstein powiedział w 1933 r.: „Nadrzędnym celem całej teorii jest uczynienie nieredukowalnych podstawowych elementów tak prostymi i jak najmniejszymi, bez konieczności rezygnacji z adekwatnej reprezentacji pojedynczej podstawy doświadczenia”. Innymi słowy, Einstein zaleca wybór najprostszej hipotezy, która pasuje do danych. Zasadę tę można prześledzić dalej od XIV-wiecznego angielskiego filozofa Williama z Ockham2. Jego zasada, że „wielości [bytów] nie należy zakładać bez konieczności” nazywa się brzytwą Ockhama, ponieważ służy do „ogolenia” wątpliwych wyjaśnień. . Zdefiniowanie prostoty nie jest łatwe. Wydaje się jasne, że wielomian z tylko dwoma parametrami jest prostszy niż jeden z trzynastoma parametrami. Która hipoteza jest najlepsza na rysunku? Nie możemy być pewni. Gdybyśmy wiedzieli, że dane reprezentują, powiedzmy, liczbę wejść na stronę internetową, która rośnie z dnia na dzień, ale także cykli w zależności od pory dnia, moglibyśmy faworyzować funkcję sinusoidalną. Gdybyśmy wiedzieli, że dane na pewno nie są cykliczne, ale mają wysoki poziom szumu, faworyzuje to funkcję liniową. W niektórych przypadkach analityk jest skłonny powiedzieć nie tylko, że hipoteza jest możliwa lub niemożliwa, ale raczej, jak bardzo jest prawdopodobna. Uczenie nadzorowane można przeprowadzić wybierając hipotezę h*, która jest najbardziej prawdopodobna, biorąc pod uwagę dane:
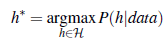
Zgodnie z regułą Bayesa jest to równoznaczne z
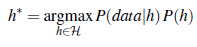
Następnie możemy powiedzieć, że prawdopodobieństwo a priori P(h) jest wysokie dla gładkiego wielomianu stopnia 1 lub -2 i niższe dla wielomianu stopnia 12 z dużymi, ostrymi skokami. Zezwalamy na nietypowo wyglądające funkcje, gdy dane mówią, że naprawdę ich potrzebujemy, ale odradzamy je, dając im niskie prawdopodobieństwo a priori. Dlaczego nie pozwolić, aby H było klasą wszystkich programów komputerowych lub wszystkich maszyn Turinga? Problem I polega na tym, że istnieje kompromis między ekspresywnością przestrzeni hipotez a złożonością obliczeniową znalezienia dobrej hipotezy w tej przestrzeni. Na przykład dopasowanie linii prostej do danych jest łatwym obliczeniem; dopasowanie wielomianów wysokiego stopnia jest nieco trudniejsze; a montaż maszyn Turinga jest nierozstrzygnięty. Drugim powodem preferowania prostych przestrzeni hipotez jest to, że prawdopodobnie będziemy chcieli użyć h po tym, jak się go nauczymy, a obliczanie h(x), gdy h jest funkcją liniową, jest gwarantowane, aby było szybkie, podczas gdy obliczanie dowolnego programu maszyny Turinga nie jest nawet gwarantowane zakończenie. Z tych powodów większość prac nad uczeniem się skupiała na prostych reprezentacjach. W ostatnich latach pojawiło się duże zainteresowanie głębokim uczeniem, gdzie reprezentacje nie są proste, ale gdzie obliczenie h(x) nadal wymaga tylko ograniczonej liczby kroków, aby wykonać obliczenia na odpowiednim sprzęcie. Zobaczymy, że kompromis między ekspresywnością a złożonością nie jest prosty: często jest tak, jak widzieliśmy z logiką pierwszego rzędu w rozdziale 8, że język ekspresyjny umożliwia dopasowanie prostej hipotezy do danych, przy jednoczesnym ograniczeniu wyrazistość języka oznacza, że każda spójna hipoteza musi być złożona.
Postęp technologiczny w zakresie przetwarzania obrazu spowodował wzrost wymagań w wielu dziedzinach aplikacji. Znaczące ulepszenia nastąpiły w rozwoju nowych algorytmów i platform przetwarzania obrazu. Niedawny rozwój technologii czujników zrewolucjonizował dziedzinę zastosowań, która pośrednio wymaga opracowania bardziej wyrafinowanych technik przetwarzania obrazu. Ponadto dostępność czujników satelitarnych i konstelacja satelitów obserwujących Ziemię na całym świecie dała ogromne możliwości modelowania powierzchni Ziemi w celu efektywnego zarządzania zasobami naturalnymi i działań monitorujących. Technologia RS stała się niezbędnym i uniwersalnym narzędziem w konfiguracji rządowej, w tym w przemyśle. Dziedzina ta przyciągnęła w ciągu ostatnich dwóch dekad wiele uwagi badawczej w zakresie innowacji technik przetwarzania obrazu. Rosnąca dostępność obrazów bezzałogowych statków powietrznych (UAV) szeregów czasowych znacznie zwiększyła częstotliwość monitorowania i zarządzania aktywnością zasobów. UAV są bardzo skutecznie wykorzystywane do monitorowania terenu w czasie rzeczywistym, częstych przeglądów; mogą szybko rejestrować obrazy w podwyższonej jakości [55]. W ciągu ostatniej dekady rynek dronów kwitł z wykładniczym wzrostem we wszystkich zakresach zastosowań, szczególnie w branży budowlanej. Najważniejszym aspektem w radzeniu sobie z analizą wielomodelową, śledzeniem obiektów w bałaganie itp. stają się nowe techniki przetwarzania danych lub modernizacja konwencjonalnych technik teledetekcyjnych [56]. Wiele obszarów zastosowań kładzie nacisk na automatyzację i minimalną interakcję między ludźmi; Techniki oparte na sztucznej inteligencji/ML stają się coraz bardziej istotne w obecnym scenariuszu. Sztuczna inteligencja i ML są kluczowymi komponentami i głównymi czynnikami napędzającymi hiperautomatyzację wraz z innymi technologiami, takimi jak narzędzia do automatyzacji procesów robotycznych. Wykorzystanie AI/ML jest stopniowo coraz bardziej powiązane z Internetem rzeczy (IoT) dla różnych zastosowań. AI, ML i DL są już wykorzystywane do tworzenia urządzeń i usług IoT w inteligentniejszy i bezpieczniejszy sposób. W ostatnim czasie podejścia oparte na DL stają się coraz bardziej odpowiednie do analizowania obrazów VHR, ponieważ wydajność zasobów obliczeniowych uległa znacznemu zwiększeniu dzięki dodaniu jednostki przetwarzania graficznego (GPU). Wprowadzono inny wariant modeli DL do obsługi danych o charakterze big data w obszarach RS. Możliwości obrazowania wysokowymiarowego przyniosły nowe możliwości i wyzwania w rozwoju klasyfikacji RS, szczególnie w przypadku bardzo podobnych spektralnie klas pokrycia terenu RYSUNEK 4.2 Klasyfikacja obszaru uniwersytetu w Pawii (ze zbiorem danych szkoleniowych TS czujnika ROSIS-3) za pomocą zoptymalizowanego RF metoda klasyfikacji klasyfikatorów. charakteryzują się zbędnymi i nieistotnymi cechami. Studium przypadku przedstawione w rozdziale kładzie nacisk na klasyfikację obrazów hiperspektralnych VHR przy użyciu podejścia zespołowego opartego na ML. Obejmuje szereg etapów przetwarzania obrazu, w których redukcja wymiarów w przestrzeni spektralnej i cech odegrała kluczową rolę w poprawie dokładności klasyfikacji. Raportuje zoptymalizowany klasyfikator RF na podstawie losowego wyboru próbek treningowych i zestawu funkcji. Proces ten zwiększył różnorodność klasyfikatorów bazowych, co skutkuje znaczną poprawą ogólnej klasyfikacji zbioru danych hiperspektralnych ROSIS-3 w porównaniu z innymi badanymi tutaj zaawansowanymi klasyfikatorami.
Dowolny składnik programu agenta można ulepszyć dzięki uczeniu maszynowemu. Ulepszenia i techniki użyte do ich wykonania zależą od tych czynników:
. Składniki tych środków obejmują:
Każdego z tych elementów można się nauczyć. Rozważmy autonomicznego agenta samochodowego, który uczy się, obserwując kierowcę. Za każdym razem, gdy kierowca hamuje, agent może poznać warunek – regułę działania określającą, kiedy należy hamować (element 1). Widząc wiele obrazów z kamer, o których mówi się, że zawierają autobusy, może nauczyć się je rozpoznawać (komponent 2). Próbując akcji i obserwując rezultaty – na przykład gwałtowne hamowanie na mokrej drodze – może poznać efekty swoich działań (komponent 3). Następnie, gdy otrzyma skargi od pasażerów, którzy zostali dogłębnie wstrząśnięci podczas podróży, może poznać użyteczny składnik swojej ogólnej funkcji użyteczności (składnik 4). Technologia uczenia maszynowego stała się standardową częścią inżynierii oprogramowania. Za każdym razem, gdy budujesz system oprogramowania, nawet jeśli nie myślisz o nim jako o agencie AI, komponenty systemu można potencjalnie ulepszyć dzięki uczeniu maszynowemu. Na przykład oprogramowanie do analizy obrazów galaktyk poddanych soczewkowaniu grawitacyjnemu zostało przyspieszone 10 milionów razy dzięki modelowi maszynowemu i zużyciu energii na chłodzenie centra danych zostały zredukowane o 40% w przypadku innego modelu uczenia maszynowego (Gao, 2014). Zdobywca nagrody Turing Award David Patterson i szef Google AI Jeff Dean ogłosili początek „złotego wieku” architektury komputerowej dzięki uczeniu maszynowemu.
Widzieliśmy kilka przykładów modeli komponentów agenta: modele atomowe, czynnikowe i relacyjne oparte na logice lub prawdopodobieństwie i tak dalej. Dla wszystkich z nich opracowano algorytmy uczenia się. Ten rozdział zakłada niewielką wcześniejszą wiedzę ze strony agenta: zaczyna od zera i uczy się na podstawie danych. Rozważamy transfer uczenia się, w którym wiedza z jednej domeny jest przenoszona do nowej domeny, dzięki czemu nauka może przebiegać szybciej przy mniejszej ilości danych. Zakładamy jednak, że projektant systemu wybiera modelowy framework, który może prowadzić do efektywnej nauki. Przejście od określonego zestawu obserwacji do ogólnej zasady nazywa się indukcją; z obserwacji, że słońce wzeszło codziennie w przeszłości, indukujemy, że słońce wzejdzie jutro. Różni się to od dedukcji, którą analizowaliśmy w rozdziale 7, ponieważ wnioski indukcyjne mogą być nieprawidłowe, podczas gdy wnioski dedukcyjne mają gwarancję poprawności, jeśli przesłanki są prawidłowe. Ten rozdział koncentruje się na problemach, w których dane wejściowe są reprezentacją podzieloną na czynniki — wektorem wartości atrybutów. Możliwe jest również, że dane wejściowe mogą być dowolnym rodzajem struktury danych, w tym atomowej i relacyjnej. Gdy wynik jest jednym ze skończonego zestawu wartości (takich jak słonecznie/pochmurno/deszcz lub prawda/fałsz), problem uczenia się nazywa się klasyfikacją. Gdy jest to liczba (na przykład temperatura jutrzejsza, mierzona jako liczba całkowita lub liczba rzeczywista), problem uczenia się ma (co prawda niejasną) nazwę regresja. Istnieją trzy rodzaje informacji zwrotnych, które mogą towarzyszyć danym wejściowym i które określają trzy główne typy uczenia się:
Zoptymalizowany klasyfikator RF został przeanalizowany zarówno przy użyciu oryginalnego zestawu danych testu treningowego (TF), jak i testu treningowego o zmniejszonej wymiarowości zbioru danych (TS). W każdym wykonaniu model RF może wybrać najlepsze cechy predykcyjne poprzez losowy wybór cech podczas każdego podziału węzła. Model RF został skalibrowany z optymalnym podzbiorem cech o wielkości m, dla którego jest on najwyższy w stosunku do najniższej wartości błędu worka przy minimalnym R w danym teście. Zaobserwowano, że wydajność zoptymalizowanego klasyfikatora RF znacznie się poprawiła w zestawie danych TS w porównaniu z oryginalnym zestawem danych TF , mimo że model został skalibrowany z obydwoma zestawami danych. Osiągnął ogólną dokładność OA = 9,45% przy P = 0,96, 
i ROC = 0,98, gdy model został przeszkolony przy użyciu zestawu danych TS. Wydajność obliczeniowa klasyfikatora RF została również zwiększona dzięki optymalnemu podzbiorowi cech m = 8 niż oryginalna pierwotna liczba cech m = 147. Zbudowanie modelu uczącego zajęło tylko 6,09 s. Dla zbioru danych TF model został skalibrowany z m = 11, co również poprawia wydajność klasyfikatora RF z oryginalnymi danymi z pełnym zestawem funkcji. Wydajność zoptymalizowanego klasyfikatora RF jest porównywana z trzema innymi potężnymi klasyfikatorami; perceptron wielowarstwowy (MLP), maszyna wektorów pomocniczych (SVM) i las rotacji.. Zaobserwowano, że ogólna wydajność wszystkich klasyfikatorów jest zwiększona, gdy zostały one przeszkolone za pomocą zestawu danych TS. Zoptymalizowany klasyfikator RF przewyższał wszystkie inne klasyfikatory zarówno dla zestawów danych TF, jak i TS. Dla porównania zarówno klasyfikatory lasu rotacji, jak i klasyfikatory SVM również wykazały zadowalający wynik niż MLP. Mocną stroną zoptymalizowanego klasyfikatora RF jest to, że obniża on koszty obliczeniowe, ponieważ wyszukuje losowo najlepszą cechę z już wybranego optymalnego podzbioru cech, a nie z całego zestawu cech. Umożliwia to również osiągnięcie wyższej wydajności w przypadkach, w których zestawy danych są powiązane z szumem lub dodatkowymi funkcjami. Wybór odpowiedniego rozmiaru klasyfikatora RF jest ważny, ponieważ decyduje o wydajności zarówno dokładności, jak i kosztów obliczeniowych. Studium przypadku zademonstrowane na hiperspektralnym zestawie danych ROSIS-3 przy użyciu zoptymalizowanego klasyfikatora RF zostało uznane za charakterystycznie lepsze i skuteczne pod względem dokładności predykcyjnej i czasu wykonania
Agent uczy się, czy poprawia swoją wydajność po dokonaniu obserwacji świata. Nauka może wahać się od trywialnych, takich jak spisanie listy zakupów, do głębokich, jak wtedy, gdy Albert Einstein wywnioskował nową teorię wszechświata. Kiedy agentem jest komputer, nazywamy to uczeniem maszynowym: komputer obserwuje pewne dane, buduje model na podstawie danych i używa modelu zarówno jako hipotezy o świecie, jak i oprogramowania, które może rozwiązać problemy. Dlaczego mielibyśmy chcieć, aby maszyna się uczyła? Dlaczego nie po prostu zaprogramować go we właściwy sposób na początek? Są dwa główne powody. Po pierwsze, projektant nie może przewidzieć wszystkich możliwych przyszłych sytuacji. Na przykład robot zaprojektowany do poruszania się po labiryntach musi nauczyć się układu każdego nowego labiryntu, jaki napotka; program do przewidywania cen na giełdzie musi nauczyć się dostosowywać, gdy warunki zmieniają się od boomu do spadku. Po drugie, czasami projektanci nie mają pomysłu na samodzielne zaprogramowanie rozwiązania. Większość ludzi jest dobra w rozpoznawaniu twarzy członków rodziny, ale robią to podświadomie, więc nawet najlepsi programiści nie wiedzą, jak zaprogramować komputer, aby wykonać to zadanie, z wyjątkiem użycia algorytmów uczenia maszynowego.