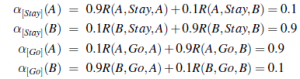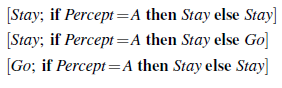Miesiąc: lipiec 2022

Podstawowy projekt agenta POMDP online jest prosty: zaczyna się od pewnego wcześniejszego stanu wiary; wybiera działanie oparte na pewnym procesie deliberacji skoncentrowanym na jego obecnym stanie przekonań; po wykonaniu działania otrzymuje obserwację i aktualizuje swój stan przekonania za pomocą algorytmu filtrującego; i proces się powtarza. Jednym z oczywistych wyborów do procesu rozważań jest algorytm expectimax , z wyjątkiem stanów przekonań, a nie stanów fizycznych jako węzłów decyzyjnych w drzewie. Węzły losowe w drzewie POMDP mają gałęzie oznaczone możliwymi obserwacjami i prowadzące do następnego stanu przekonania, z prawdopodobieństwem przejścia podanym przez równanie. Fragment drzewa oczekiwania-stanu przekonania dla POMDP 4 x 3 pokazano na rysunku.

Złożoność czasowa wyczerpującego poszukiwania do głębokości d wynosi O (|A|^d · |E|^d), gdzie |A| to liczba dostępnych akcji, a |E| to liczba możliwych perceptów. (Zauważ, że jest to znacznie mniej niż liczba możliwych planów warunkowych głębokości d generowanych przez iterację wartości). Podobnie jak w przypadku obserwowalnym, próbkowanie w węzłach losowych jest dobrym sposobem na zmniejszenie współczynnika rozgałęzienia bez utraty zbyt dużej dokładności w ostateczna decyzja. Zatem złożoność przybliżonego podejmowania decyzji online w POMDP może nie być drastycznie gorsza niż w przypadku MDP. W przypadku bardzo dużych przestrzeni stanów dokładne filtrowanie jest niewykonalne, więc agent będzie musiał uruchomić przybliżony algorytm filtrowania, taki jak filtrowanie cząstek (patrz strona 510). Wtedy przekonania w drzewie oczekiwanym stają się zbiorami cząstek, a nie dokładnymi rozkładami prawdopodobieństwa. W przypadku problemów z długimi horyzontami konieczne może być również uruchomienie rozgrywania dalekiego zasięgu stosowanego w algorytmie UCT. Połączenie filtrowania cząstek i UCT zastosowane w POMDP nosi nazwę częściowo obserwowalnego planowania Monte Carlo lub POMCP. Z reprezentacją DDN dla modelu, algorytm POMCP ma, przynajmniej w zasadzie, zastosowanie do bardzo dużych i realistycznych POMDP. POMCP jest w stanie generować właściwe zachowanie w 4 x 3 POMDP. Krótki (i nieco szczęśliwy) przykład pokazano na rysunku

Agenci POMDP oparte na dynamicznych sieciach decyzyjnych i podejmowaniu decyzji online mają szereg zalet w porównaniu z innymi, prostszymi projektami agentów przedstawionymi we wcześniejszych rozdziałach. W szczególności zajmują się częściowo obserwowalnymi, stochastycznymi środowiskami i mogą łatwo zrewidować swoje „plany”, aby poradzić sobie z nieoczekiwanymi dowodami. Dzięki odpowiednim modelom czujników mogą poradzić sobie z awarią czujnika i planować zbieranie informacji. Wykazują „wdzięczną degradację” pod presją czasu i w złożonych środowiskach, przy użyciu różnych technik aproksymacyjnych. Więc czego brakuje? Główną przeszkodą we wdrażaniu takich agentów w świecie rzeczywistym jest niemożność generowania udanego zachowania w długich skalach czasowych. Losowe lub prawie losowe zagrania nie mają nadziei na uzyskanie jakiejkolwiek pozytywnej nagrody za, powiedzmy, zadanie nakrycia stołu do kolacji, co może wymagać dziesiątek milionów działań związanych z kontrolą motoryczną. Wydaje się konieczne zapożyczenie niektórych pomysłów dotyczących planowania hierarchicznego.

Z biegiem lat naukowcy odkryli, że ludzie coraz bardziej przywiązują się do urządzeń technologicznych w swoim życiu. Cofnij się… pamiętasz ostatni raz, kiedy spędziłeś cały dzień bez smartfona? Jak byś się czuł, gdybyś musiał zrezygnować z telefonu od jutra? Thomas Friedman, autor bestsellerów i trzykrotny zdobywca nagrody Pulitzera, ma wyjątkowy talent do analizowania rozwoju technologicznego i jego wpływu na społeczeństwo. W swojej książce “Dziękujemy za spóźnienie” przypomina nam, że niezwykle ważne jest połączenie rozwoju technologicznego, w tym rozwoju sztucznej inteligencji i innych technologii wykładniczych, “ze wszystkimi rzeczami, których nie można pobrać – dobrymi wartościami, dobrym nauczaniem, dobrym edukowanie, rzeczy, które wymagają czasu i są powolne “i że jeśli tego nie zrobimy, będziemy mieli kłopoty jako społeczeństwo. Nasze smartfony dają nam natychmiastowy dostęp do ogromnej ilości informacji, pomagają nam skuteczniej komunikować się i rozwiązywać trudne problemy, ale ciągłe używanie z czasem wiąże się również z pewną ceną. Niedawny raport wskazuje, że chirurgowie kręgosłupa zaobserwowali wzrost liczby pacjentów z bólem szyi i pleców, co może być spowodowane problemami z postawą, które często wynikają z częstego używania smartfonów. Większość ludzi uważa, że nie są w stanie odłączyć się od telefonu. To tylko jeden z przykładów długoterminowych wyzwań związanych z wykorzystaniem nowych technologii. Podobna sytuacja staje się widoczna wraz z rozwojem mediów społecznościowych. Chociaż platformy mediów społecznościowych mogą zapewniać nam sieci, za pośrednictwem których możemy komunikować się i udostępniać informacje, mogą mieć również wady społecznościowe. Według psychologów w Wielkiej Brytanii na przykład nadmierne korzystanie z mediów społecznościowych jest bezpośrednio związane ze zwiększonym poczuciem samotności. W rzeczywistości niektóre osoby spędzają już więcej czasu na interakcjach ze swoimi komputerami lub ekranami smartfonów niż z innymi ludźmi. Dla innych obserwowanie, ile “polubień” dostaje ich zdjęcie na Instagramie, stało się ważniejsze niż interakcje społeczne w prawdziwym życiu. To tylko niektóre przykłady sposobów, w jakie technologia może powodować problemy, gdy nie jest używana z umiarem. Jeśli nie będziemy przestrzegać zaleceń dotyczących umiarkowanego użytkowania, bardzo prawdopodobne jest, że podobne problemy wystąpią w przypadku technologii sztucznej inteligencji. Na przykład w przyszłości inteligentni asystenci osobiści, tacy jak Siri i Google Assistant, będą znacznie bardziej wydajni, wykonując niemal każde zadanie, nawet komunikując się z naszymi przyjaciółmi. Jeśli polegamy na narzędziach sztucznej inteligencji, aby zrobić wszystko dla nas, ta nadmierna zależność może zagrozić niektórym z tych cech, które czynią nas ludźmi, na przykład zdolność do tworzenia więzi społecznych, co z kolei może mieć negatywne konsekwencje dla nas jako jednostki i społeczeństwa . Chociaż sztuczna inteligencja oferuje ogromny potencjał dla zmieniających życie aplikacji, powinna być nadal stosowana z umiarem. Przede wszystkim AI należy wykorzystywać do tworzenia rozwiązań, dzięki którym ludzie mogą wykorzystać to, co czyni ich wyjątkowo ludzkimi.

Opisaliśmy algorytm iteracji wartości, który oblicza jedną wartość użyteczności dla każdego stanu. Przy nieskończenie wielu stanach wiary musimy być bardziej kreatywni. Rozważ optymalną politykę π* i jej zastosowanie w określonym stanie przekonań b: polityka generuje działanie, następnie dla każdego kolejnego spostrzeżenia stan przekonania jest aktualizowany i generowane jest nowe działanie, i tak dalej. W przypadku tego konkretnego b polityka jest zatem dokładnie równoważna z planem warunkowym, dla niedeterministycznych i częściowo obserwowalnych problemów. Zamiast myśleć o zasadach, pomyślmy o planach warunkowych i o tym, jak oczekiwana użyteczność wykonania ustalonego planu warunkowego zmienia się wraz z początkowym stanem przekonań. Dokonujemy dwóch obserwacji:

1. Niech użyteczność wykonania ustalonego planu warunkowego p rozpoczynającego się w stanie fizycznym s będzie α_p(s). Wtedy oczekiwana użyteczność wykonania p w stanie przekonania b jest po prostu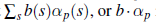   

jeśli pomyślimy o nich obu jako o wektorach. Zatem oczekiwana użyteczność ustalonego planu warunkowego zmienia się liniowo z b; to znaczy, odpowiada hiperpłaszczyźnie w przestrzeni przekonań.

2. W dowolnym stanie b przekonań optymalna polityka wybierze wykonanie planu warunkowego z najwyższą oczekiwaną użytecznością; a oczekiwana użyteczność b przy optymalnej polityce jest po prostu użytecznością tego planu warunkowego: U(b) = U^π*(b) = max_pb·α_p. Jeśli optymalna polityka π* zdecyduje się na wykonanie p zaczynając od b, wówczas rozsądne jest oczekiwanie, że może wybrać wykonanie p w stanach przekonań, które są bardzo bliskie b; w rzeczywistości, jeśli ograniczymy głębokość planów warunkowych, to takich planów jest tylko skończenie wiele, a ciągła przestrzeń stanów przekonań będzie generalnie podzielona na regiony, z których każdy odpowiada określonemu planowi warunkowemu, który jest optymalny w tym regionie.

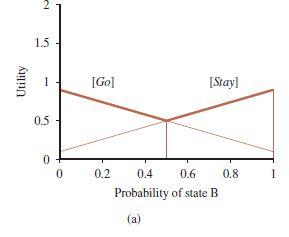
Z tych dwóch obserwacji widzimy, że funkcja użyteczności U(b) w stanach przekonań, będąca maksimum zbioru hiperpłaszczyzn, będzie odcinkowo liniowa i wypukła. Aby to zilustrować, posłużymy się prostym światem dwustanowym. Stany są oznaczone jako A i B i są dwie akcje: Stay pozostaje w miejscu z prawdopodobieństwem 0,9, a Go przełącza się do drugiego stanu z prawdopodobieństwem 0,9. Nagrodami są R (·,·, A) = 0 i R (·,·, B) = 1; oznacza to, że każde przejście kończące się na A ma nagrodę zero, a każde przejście kończące się na B ma nagrodę 1. Na razie przyjmiemy współczynnik dyskontowy γ = 1. Czujnik zgłasza prawidłowy stan z prawdopodobieństwem 0,6. Oczywiście agent powinien zostać, gdy jest w stanie B, i iść, gdy jest w stanie A. Problem w tym, że nie wie, gdzie jest! Zaletą świata dwustanowego jest to, że przestrzeń przekonań może być wizualizowana w jednym wymiarze, ponieważ dwa prawdopodobieństwa b (A) i b (B) sumują się do 1. Na rysunku (a) oś x reprezentuje stan przekonania, zdefiniowany przez b (B), prawdopodobieństwo bycia w stanie B.

Rozważmy teraz jednoetapowe plany [Stay] i [Go], z których każdy otrzymuje nagrodę za jedno przejście w następujący sposób:

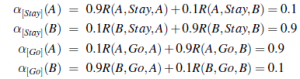
Hiperpłaszczyzny (linie, w tym przypadku) dla b·α_[Stay] i b·α_[Go] są pokazane na rysunku (a), a ich maksimum jest pogrubione. Pogrubiona linia reprezentuje zatem funkcję użyteczności dla problemu skończonego horyzontu, która umożliwia tylko jedno działanie, a w każdym „kawałku” odcinkowo liniowej funkcji użyteczności działaniem optymalnym jest pierwsze działanie odpowiadającego planu warunkowego. W tym przypadku optymalna jednoetapowa polityka to Pozostań, gdy b(B)> 0.5 i Idź w przeciwnym razie. Kiedy już mamy użyteczność p (s) dla wszystkich planów warunkowych p głębokości 1 w każdym stanie fizycznym s, możemy obliczyć użyteczności dla planów warunkowych o głębokości 2, biorąc pod uwagę każdą możliwą pierwszą akcję, każdą możliwą następną percepcję, a następnie każdy sposób wyboru planu głębokości-1 do wykonania dla każdej percepcji:

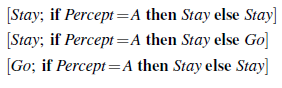
W sumie istnieje osiem odrębnych planów głębokości 2, a ich użyteczność pokazano na rysunku (b).

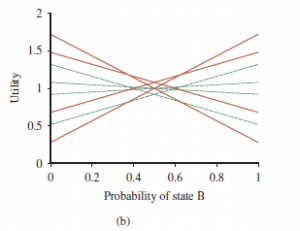
Zauważ, że cztery plany, pokazane jako linie przerywane, są nieoptymalne w całej przestrzeni przekonań – mówimy, że te plany są zdominowane i nie trzeba ich dalej rozważać. Istnieją cztery niezdominowane plany, z których każdy jest optymalny w określonym regionie, jak pokazano na rysunku (c).

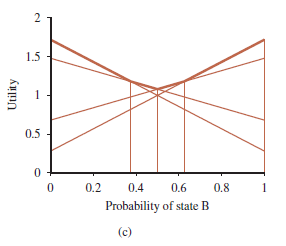
Regiony dzielą przestrzeń stanów przekonań. Powtarzamy proces dla głębokości 3 i tak dalej. Ogólnie rzecz biorąc, niech p będzie planem warunkowym o głębokości d, którego działaniem początkowym jest a i którego podplanem głębokości (d-1) dla percepcji e jest p.e; następnie

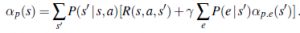
Ta rekurencja w naturalny sposób daje nam algorytm iteracji wartości, który pokazano na rysunku. Struktura algorytmu i jego analiza błędów są podobne do algorytmu iteracji wartości podstawowej na Rysunku 16.6 na stronie 563; główna różnica polega na tym, że zamiast obliczać jeden numer użyteczności dla każdego stanu, POMDP-VALUE-ITERATION utrzymuje zbiór niezdominowanych planów z ich hiperpłaszczyznami użyteczności. Złożoność algorytmu zależy przede wszystkim od tego, ile planów zostanie wygenerowanych. Biorąc pod uwagę działania |A| i możliwe obserwacje |E|, istnieją odrębne plany głębokościowe |A|^O(|E|d-1). Nawet dla skromnego, dwupaństwowego świata z d = 8, to jest 2²⁵⁵ planów. Eliminacja planów zdominowanych jest niezbędna dla zmniejszenia tego podwójnie wykładniczego wzrostu: liczba planów niezdominowanych z d = 8 wynosi zaledwie 144. Funkcja użyteczności dla tych 144 planów jest pokazana na rysunku (d).

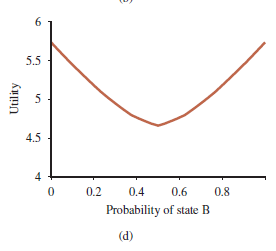
Zauważ, że pośrednie stany przekonań mają niższą wartość niż stan A i stan B, ponieważ w stanach pośrednich agentowi brakuje informacji potrzebnych do wyboru dobrego działania. Dlatego informacja ma wartość ,a optymalne polityki w POMDP często obejmują działania mające na celu gromadzenie informacji.

Mając taką funkcję użyteczności, można wyodrębnić wykonywalną politykę, sprawdzając, która hiperpłaszczyzna jest optymalna w dowolnym stanie przekonania b i wykonując pierwsze działanie odpowiadającego planu. Na rysunku (d) odpowiednia optymalna polityka jest nadal taka sama jak dla planów głębokości 1: Zostań, gdy b(B)> 0,5 i idź w przeciwnym razie. W praktyce algorytm iteracji wartości na rysunku jest beznadziejnie nieefektywny w przypadku większych problemów – nawet POMDP 4×3 jest zbyt trudny.

Głównym powodem jest to, że mając n niezdominowanych planów warunkowych na poziomie d, algorytm konstruuje plany warunkowe |A|· n^|E| na poziomie d+1 przed wyeliminowaniem planów zdominowanych. Przy czujniku czterobitowym |E| wynosi 16, a n może być w setkach, więc jest to beznadziejne. Od czasu opracowania tego algorytmu w latach 70. nastąpiło kilka postępów, w tym bardziej wydajne formy iteracji wartości i różne rodzaje algorytmów iteracji polityki. Niektóre z nich omówiono w uwagach na końcu rozdziału. Jednak w przypadku ogólnych POMDP znalezienie optymalnej polityki jest bardzo trudne (w rzeczywistości trudna do PSPACE — to znaczy bardzo trudna). W następnej sekcji opisano inną, przybliżoną metodę rozwiązywania POMDP, opartą na wyszukiwaniu z wyprzedzeniem.