Na razie będziemy traktować ustawienia multiefektorowe, wieloobiektowe i wieloagentowe w ten sam sposób, oznaczając je ogólnie jako ustawienia wieloaktorowe, używając ogólnego terminu aktor na określenie efektorów, ciał i agentów. Celem tej sekcji jest wypracowanie sposobu definiowania modeli przejścia, poprawnych planów i wydajnych algorytmów planowania dla ustawienia wieloaktorowego. Prawidłowy plan to taki, który, wykonany przez aktorów, osiąga cel. (W prawdziwym środowisku wieloagentowym agenci mogą oczywiście nie zgodzić się na wykonanie konkretnego planu, ale przynajmniej będą wiedzieć, jakie plany zadziałałyby, gdyby zgodzili się na ich wykonanie). satysfakcjonującym modelem działania wieloagentowego jest to, że musimy jakoś poradzić sobie z drażliwą kwestią współbieżności, przez co rozumiemy po prostu, że plany każdego agenta mogą być realizowane jednocześnie. Jeśli mamy myśleć o realizacji planów wielopodmiotowych, to najpierw potrzebujemy modelu planów wielopodmiotowych, który zawiera zadowalający model współbieżnego działania. Ponadto działanie wielopodmiotowe wiąże się z całym zestawem problemów, które nie są przedmiotem planowania z jednym agentem. W szczególności agenci muszą brać pod uwagę sposób, w jaki ich własne działania J oddziałują z działaniami innych agentów. Na przykład agent będzie musiał rozważyć, czy działania wykonywane przez innych agentów mogą zakłócić warunki wstępne jego własnych działań, czy zasoby, z których korzysta podczas wykonywania jego zasad, mogą być współdzielone, czy też mogą zostać wyczerpane przez innych agentów; czy działania wzajemnie się wykluczają; a pomocniczo nastawiony agent może zastanowić się, w jaki sposób jego działania mogą ułatwić działania innych. Aby odpowiedzieć na te pytania, potrzebujemy modelu współbieżnego działania, w ramach którego możemy je właściwie sformułować. Modele współbieżnego działania były głównym przedmiotem badań w głównym nurcie społeczności informatycznej od dziesięcioleci, ale żaden ostateczny, powszechnie akceptowany model nie przetrwał. Niemniej jednak następujące trzy podejścia stały się szeroko rozpowszechnione.
Pierwsze podejście polega na rozważeniu wykonania działań z przeplotem w odpowiednich. Pierwsze podejście polega na rozważeniu wykonania działań z przeplotem w odpowiednich planach. Załóżmy na przykład, że mamy dwóch agentów, A i B, z następującymi planami:
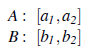
Kluczową ideą modelu realizacji z przeplotem jest to, że jedyną rzeczą, której możemy być pewni w realizacji planów dwóch agentów, jest zachowanie kolejności działań w poszczególnych planach. Jeśli dalej założymy, że akcje są niepodzielne, to istnieje sześć różnych sposobów, w jakie dwa powyższe plany mogą być wykonywane jednocześnie:
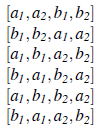
Aby plan był poprawny w modelu wykonania z przeplotem, musi być poprawny w odniesieniu do wszystkich możliwych przeplatań planów. Model wykonywania z przeplotem został powszechnie przyjęty w społeczności zajmującej się współbieżnością, ponieważ jest to rozsądny model sposobu, w jaki wiele wątków na zmianę działa na jednym procesorze. Nie modeluje jednak przypadku, w którym dwie czynności mają miejsce w tym samym czasie. Co więcej, liczba sekwencji z przeplotem będzie rosła wykładniczo wraz z liczbą agentów i akcji: w konsekwencji sprawdzenie poprawności planu, co jest proste obliczeniowo w ustawieniach z jednym agentem, jest trudne obliczeniowo w modelu wykonania z przeplotem.
Drugie podejście to prawdziwa współbieżność, w której nie próbujemy tworzyć pełnej zserializowanej kolejności akcji, ale pozostawiamy je częściowo uporządkowane: wiemy, że a1 wystąpi przed a2, ale w odniesieniu do kolejności a1 i b1, ponieważ na przykład nie możemy nic powiedzieć; jedno może wystąpić przed drugim lub może wystąpić jednocześnie. Zawsze możemy „spłaszczyć” model częściowego rzędu współbieżnych planów do modelu z przeplotem, ale w ten sposób tracimy informacje o częściowym porządku. Chociaż modele częściowego rzędu są prawdopodobnie bardziej satysfakcjonujące niż modele z przeplotem jako teoretyczne ujęcie współbieżnego działania, nie zostały one tak powszechnie przyjęte w praktyce.
Trzecie podejście polega na założeniu idealnej synchronizacji: istnieje zegar globalny, do którego każdy agent ma dostęp, każde działanie zajmuje tyle samo czasu, a działania w każdym punkcie wspólnego planu są równoczesne. W ten sposób akcje każdego agenta są wykonywane synchronicznie, we wzajemnej blokadzie (może być tak, że niektórzy agenci wykonują akcję no-op, gdy czekają na zakończenie innych akcji). Wykonywanie synchroniczne nie jest bardzo kompletnym modelem współbieżności w świecie rzeczywistym, ale ma prostą semantykę i z tego powodu jest to model, z którym będziemy tutaj pracować.
Zaczynamy od modelu przejścia; dla przypadku deterministycznego jednoagentowego jest to funkcja RESULT(i, a), która podaje stan wynikający z wykonania akcji a, gdy środowisko znajduje się w stanie s. W ustawieniu z jednym agentem mogą istnieć b różne opcje działania; b może być dość duży, szczególnie w przypadku reprezentacji pierwszego rzędu z wieloma obiektami, na których można działać, ale schematy działań zapewniają jednak zwięzłą reprezentację. W układzie wielopodmiotowym z n aktorami pojedyncze działanie a zostaje zastąpione wspólnym działaniem <a1,…, an>, gdzie ai jest akcją podjętą przez i-tego aktora. Od razu widzimy dwa problemy: po pierwsze, musimy opisać model przejścia dla bn różnych wspólnych działań; po drugie, mamy wspólny problem z planowaniem o współczynniku rozgałęzienia bn. Po umieszczeniu aktorów w systemie wielopodmiotowym z ogromnym czynnikiem rozgałęzienia, głównym celem badań nad planowaniem wielopodmiotowym było oddzielenie aktorów w możliwie największym stopniu, tak aby (idealnie) złożoność problemu rosła liniowo wraz z n, a nie wykładniczo z bn. Jeśli aktorzy nie wchodzą ze sobą w interakcje – na przykład n aktorów gra w pasjansa – wtedy możemy po prostu rozwiązać n oddzielnych problemów. Jeśli aktorzy są luźno powiązani, czy możemy osiągnąć coś zbliżonego do tej wykładniczej poprawy? Jest to oczywiście centralne pytanie w wielu obszarach sztucznej inteligencji. Widzieliśmy skuteczne metody rozwiązywania luźno sprzężonych systemów w kontekście CSP, gdzie „drzewopodobne” grafy ograniczeń dawały wydajne metody rozwiązywania, a także w kontekście rozłącznych baz danych wzorców i heurystyk addytywnych do planowania. Standardowym podejściem do luźno powiązanych problemów jest udawanie, że problemy są całkowicie oddzielone, a następnie naprawienie interakcji. Dla modelu przejścia oznacza to pisanie schematów działania tak, jakby aktorzy działali niezależnie. Zobaczmy, jak to działa w przypadku gry w tenisa podwójnego. Tutaj mamy dwóch ludzkich tenisistów, którzy tworzą drużynę deblową, której wspólnym celem jest wygranie meczu z przeciwną drużyną. Załóżmy, że w pewnym momencie gry drużyna ma na celu oddanie do niej trafionej piłki i upewnienie się, że przynajmniej jeden z nich kryje siatkę. Rysunek przedstawia warunki początkowe, cele i schematy działania dla tego problemu.

Łatwo zauważyć, że możemy przejść od warunków początkowych do celu dzięki dwuetapowemu wspólnemu planowi, który określa, co każdy gracz ma zrobić: A powinien przesunąć się na prawą linię bazową i uderzyć piłkę, podczas gdy B powinien po prostu zostać umieścić w sieci:
![]()
Problemy pojawiają się jednak, gdy plan nakazuje, aby obaj agenci uderzali piłkę w tym samym czasie. W prawdziwym świecie to nie zadziała, ale schemat działania Hit mówi, że piłka zostanie pomyślnie zwrócona. Trudność polega na tym, że warunki wstępne ograniczają stan, w którym działanie samo w sobie może być pomyślnie wykonane, ale nie ograniczają innych współbieżnych działań, które mogą je zepsuć. Rozwiązujemy ten problem, rozszerzając schematy akcji o jedną nową cechę: ograniczenie współbieżnej akcji, określające, które akcje muszą lub nie mogą być wykonywane jednocześnie. Na przykład akcję Hit można opisać w następujący sposób:

Innymi słowy, akcja trafienia ma określony efekt tylko wtedy, gdy żadna inna akcja trafienia innego agenta nie występuje w tym samym czasie. (W podejściu SATPLAN byłoby to obsługiwane przez aksjomat wykluczenia działania częściowego). W przypadku niektórych działań pożądany efekt jest osiągany tylko wtedy, gdy inne działanie występuje jednocześnie. Np. dwóch agentów jest potrzebnych do wniesienia lodówki z napojami na kort tenisowy:
![]()
W przypadku tego rodzaju schematów działania każdy z algorytmów planowania można zaadaptować z niewielkimi modyfikacjami w celu wygenerowania planów wielopodmiotowych. W zakresie, w jakim sprzężenie między planami podrzędnymi jest luźne – co oznacza, że ograniczenia współbieżności wchodzą w grę tylko rzadko podczas wyszukiwania planów – można by oczekiwać, że różne heurystyki opracowane dla planowania z jednym agentem będą również skuteczne w kontekście wielopodmiotowym.