Miesiąc: lipiec 2022

Zwróciliśmy uwagę na znaczenie projektowania systemów sztucznej inteligencji, które mogą działać w warunkach niepewności co do prawdziwego celu człowieka. Wprowadziliśmy prosty model niepewności co do własnych preferencji na przykładzie lodów o smaku duriana. Dzięki prostemu urządzeniu dodawania do modelu nowej zmiennej utajonej reprezentującej nieznane preferencje, wraz z odpowiednim modelem czujnika (np. obserwacja smaku małej próbki lodów), niepewne preferencje mogą być obsługiwane w naturalny sposób . Zbadano również problem wyłącznika: pokazaliśmy, że robot z niepewnością co do ludzkich preferencji będzie ulegał człowiekowi i pozwoli się wyłączyć. W tym problemie Robbie robot nie jest pewien preferencji Harriet człowieka, ale modelujemy decyzję Harriet (czy wyłączyć Robbiego, czy nie) jako prostą, deterministyczną konsekwencję jej własnych preferencji dotyczących działania, które proponuje Robbie. Tutaj uogólniamy ten pomysł na pełną grę dla dwóch osób, zwaną grą asystującą, w której zarówno Harriet, jak i Robbie są graczami. Zakładamy, że Harriet obserwuje własne preferencje θ i postępuje zgodnie z nimi, podczas gdy Robbie ma prawdopodobieństwo a priori P( θ ) przed preferencjami Harriet. Wypłata jest zdefiniowana przez θ i jest identyczna dla obu graczy: zarówno Harriet, jak i Robbie maksymalizują wypłatę Harriet. W ten sposób gra pomocowa dostarcza formalnego modelu idei dającej się udowodnić korzystnej sztucznej inteligencji, wprowadzonej w Rozdziale 1. Oprócz deferencyjnego zachowania wykazywanego przez Robbiego w problemie wyłączania – strategie wyłaniania się jako równowagi w ogólnych grach pomocowych obejmują działania na Część Harriet, którą opisalibyśmy jako nauczanie, nagradzanie, dowodzenie, poprawianie, demonstrowanie lub wyjaśnianie, a także działania ze strony Robbiego, które określilibyśmy jako proszenie o pozwolenie, uczenie się na pokazach, wywoływanie preferencji i tak dalej. Kluczową kwestią jest to, że te zachowania nie muszą być oskryptowane: rozwiązując grę, Harriet i Robbie opracowują sami, jak przekazać informacje o preferencjach od Harriet do Robbiego, aby Robbie mógł być bardziej użyteczny dla Harriet. Nie musimy z góry ustalać, że Harriet ma „dawać nagrody” lub że Robbie ma „postępować zgodnie z instrukcjami”, chociaż mogą to być rozsądne interpretacje tego, jak ostatecznie się zachowują. Aby zilustrować gry asystujące, użyjemy gry ze spinaczami. To bardzo prosta gra, w której człowiek Harriet ma motywację do „zasygnalizowania” robotowi Robbiemu informacji o swoich preferencjach. Robbie jest w stanie zinterpretować ten sygnał, ponieważ potrafi rozwiązać grę i dlatego może zrozumieć, co musiałoby być prawdą w preferencjach Harriet, aby mogła sygnalizować w ten sposób. Etapy gry są przedstawione na rysunku.

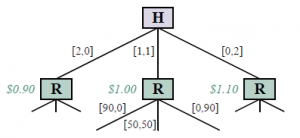
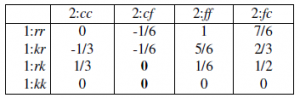
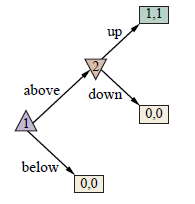
Polega na robieniu spinaczy i zszywek. Preferencje Harriet są wyrażane przez funkcję wypłaty, która zależy od liczby spinaczy do papieru i liczby wyprodukowanych zszywek, z pewnym „kursem wymiany” między nimi. Parametr preferencji θ Harriet oznacza względną wartość (w dolarach) spinacza; na przykład spinacze mogą wyceniać  θ =0:45 dolara, co oznacza, że ​​zszywki są warte 1 – θ  =0:55 dolara. Tak więc, jeśli wyprodukowanych zostanie p spinaczy i zszywek s, zysk Harriet wyniesie w sumie pθ + s(1-θ ) dolarów. A priori Robbiego to P(θ ) = Uniform( θ;0,1). W samej grze Harriet jest pierwsza i może zrobić dwa spinacze do papieru, dwie zszywki lub po jednym z każdego. Następnie Robbie może zrobić 90 spinaczy, 90 zszywek lub 50 sztuk każdego. Zauważ, że gdyby robiła to sama, Harriet zrobiłaby tylko dwie zszywki o wartości 1,10 dolara. (Patrz adnotacje na pierwszym poziomie drzewa na rysunku 17.6) Ale Robbie patrzy i uczy się z jej wyboru. Czego dokładnie się uczy? Cóż, to zależy od tego, jak Harriet dokona wyboru. Jak Harriet dokonuje wyboru? To zależy od tego, jak Robbie to zinterpretuje. Możemy rozwiązać tę cykliczność, znajdując równowagę Nasha. W tym przypadku jest wyjątkowy i można go znaleźć, stosując najlepszą odpowiedź krótkowzroczną: wybierz dowolną strategię dla Harriet; wybierz najlepszą strategię dla Robbiego, biorąc pod uwagę strategię Harriet; wybrać najlepszą strategię dla Harriet, biorąc pod uwagę strategię Robbiego; i tak dalej. Proces przebiega następująco:

1. Zacznij od zachłannej strategii dla Harriet: zrób dwa spinacze, jeśli woli spinacze; zrób po jednym z każdej, jeśli jest obojętna; zrób dwie zszywki, jeśli woli zszywki.
2. Istnieją trzy możliwości, które Robbie musi rozważyć, biorąc pod uwagę tę strategię dla Harriet:

(a) Jeśli Robbie widzi, jak Harriet robi dwa spinacze, wnioskuje, że woli spinacze, więc teraz uważa, że ​​wartość spinacza jest równomiernie rozłożona między 0,5 a 1,0, ze średnią 0,75. W takim przypadku jego najlepszym planem jest zrobienie 90 spinaczy o oczekiwanej wartości 67,50 dolarów dla Harriet.

(b) Jeśli Robbie widzi, że Harriet robi po jednym z nich, wywnioskuje, że spinacze i zszywki ceni sobie na 0,50, więc najlepszym wyborem jest zrobienie po 50 sztuk.

(c) Jeśli Robbie widzi, że Harriet robi dwie zszywki, to według tego samego argumentu, co w (a), powinien zrobić 90 zszywek.

3. Biorąc pod uwagę tę strategię dla Robbiego, najlepsza strategia Harriet różni się teraz nieco od strategii zachłannej z kroku 1. Jeśli Robbie ma zamiar zareagować na zrobienie przez nią jednego z nich, robiąc po 50 sztuk każdego nie tylko, jeśli jest dokładnie obojętna, ale jeśli jest prawie obojętna. W rzeczywistości optymalna polityka polega teraz na zrobieniu jednego z nich, jeśli ceni sobie spinacze do papieru gdzieś między około 0,446 a 0,554.
4. Biorąc pod uwagę tę nową strategię dla Harriet, strategia Robbiego pozostaje niezmieniona. Na przykład, jeśli wybierze jeden z nich, wywnioskuje, że wartość spinacza jest równomiernie rozłożona między 0,446 a 0,554, ze średnią 0,50, więc najlepszym wyborem jest zrobienie 50 sztuk każdego. Ponieważ strategia Robbiego jest taka sama jak w kroku 2, najlepsza odpowiedź Harriet będzie taka sama jak w kroku 3 i znaleźliśmy równowagę.

Dzięki swojej strategii Harriet w efekcie uczy Robbiego swoich preferencji, używając prostego kodu – języka, jeśli chcesz – wyłaniającego się z analizy równowagi. Zauważ też, że Robbie nigdy nie poznaje dokładnie preferencji Harriet, ale uczy się wystarczająco, by działać optymalnie w jej imieniu – tj. zachowuje się tak, jak gdyby dokładnie znał jej preferencje. Jest on ewidentnie korzystny dla Harriet zgodnie z podanymi założeniami i przy założeniu, że Harriet gra poprawnie. Najlepsza odpowiedź krótkowzroczna działa w tym przykładzie i innych, ale nie w bardziej złożonych przypadkach. Można wykazać, że przy braku powiązań powodujących problemy z koordynacją znalezienie optymalnego profilu strategii gry pomocowej sprowadza się do rozwiązania POMDP, którego przestrzeń stanów jest podstawową przestrzenią stanów gry plus parametry preferencji człowieka θ. Ogólnie rzecz biorąc, POMDP są bardzo trudne do rozwiązania (sekcja 16.5), ale POMDP reprezentujące gry asystujące mają dodatkową strukturę, która umożliwia bardziej wydajne algorytmy. Gry asystujące można uogólnić, aby umożliwić wielu ludzkim uczestnikom, wielu robotom, niedoskonale racjonalnym ludziom, ludziom, którzy nie znają własnych preferencji i tak dalej. Zapewniając podzieloną na czynniki lub ustrukturyzowaną przestrzeń działania, w przeciwieństwie do prostych akcji atomowych w grze w spinacze, możliwości komunikacji można znacznie zwiększyć. Niewiele z tych odmian zostało dotychczas zbadanych, ale spodziewamy się, że kluczowa właściwość gier asystujących pozostanie prawdziwa: im inteligentniejszy robot, tym lepszy wynik dla człowieka.

Niestety odpowiedź na to pytanie brzmi “tak”. Rozważ niektóre narzędzia używane w całej historii. W wielu przypadkach zostały one najpierw stworzone, aby pomóc ludziom w wykonywaniu zadań lepiej lub szybciej, ale później zostały również dostosowane do celów wojennych. W miarę rozwoju sztucznej inteligencji i robotyki organizacje wojskowe najprawdopodobniej dowiedzą się, w jaki sposób można je wykorzystać dla ich korzyści. W sierpniu 2017 r. Elon Musk wraz ze 116 dyrektorami generalnymi i badaczami AI z kolekcji 26 krajów zebrali się, aby podpisać list otwarty z prośbą do ONZ o zakaz używania broni AI. Możesz zobaczyć zawartość tego listu, a także nazwiska osób, które go podpisały, pod adresem: https://futureoflife.org/autonomous-weapons-openletter-2017

Jedna ważna linijka tego listu otwartego mówi, że:

“Po opracowaniu [śmiercionośnej broni autonomicznej] pozwoli to konflikt zbrojny, który ma być toczony na skalę większą niż kiedykolwiek, i w czasach szybszych niż ludzie są w stanie pojąć. Po otwarciu tej skrzynki Pandory trudno będzie ją zamknąć. Dlatego prosimy Wysokie Umawiające się Strony, aby znalazły sposób na ochronę nas wszystkich przed tymi zagrożeniami.”

Mamy nadzieję, że wsparcie zdobyte przez liderów w dziedzinie robotyki i sztucznej inteligencji zachęci innych przedstawicieli branży do pójścia w ich ślady. Podobny list otwarty, opublikowany przez Toby&′ego Walsha, ostrzega kraje przed rozpoczęciem wojskowego wyścigu zbrojeń AI. Ten list został podpisany przez 3 105 badaczy z branży AI i robotyki, a także 17 701 innych. Możesz zobaczyć list i podpisać go na: https://futureoflife.org/open-letter-autonomous-weapons .Max Tegmark, założyciel Future of Life Institute, ostrzega, że musimy odpowiednio przygotować się na przyszłość poprzez postęp Sztuczna inteligencja za pierwszym razem. Według Tegmarka, przy innych wynalazkach i odkryciach, takich jak ogień, ludzie mieli okazję popełniać błędy i uczyć się na ich podstawie, ale nie mamy tego luksusu dzięki zaawansowanej super AI. W dziedzinie zaawansowanych super AI nawet małe błędy w planowaniu mogą prowadzić do dużych problemów w przyszłości. Aby temu zapobiec, Tegmark zachęca wszystkich zaangażowanych do “bezpieczeństwa Inżynierii.” Kluczowymi tego przykładami byłyby zakaz używania śmiercionośnej autonomicznej broni i zapewnienie, że korzyści generowane przez AI są sprawiedliwie rozłożone w całym społeczeństwie. Ponadto, jeśli chcesz śledzić i dowiedzieć się więcej na temat tego rodzaju problemów, zachęcam do zaangażowania się w Future of Life Institute, który można znaleźć na stronie: https://futureoflife.org/getinvolved/

Kluczową cechą rozbudowanej formy, która odróżnia ją od drzew gry,  jest to, że może uchwycić częściową obserwowalność. Teoretycy gier używają terminu niedoskonałe informacje do opisania sytuacji, w których gracze nie są pewni rzeczywistego stanu gry. Niestety, indukcja wsteczna nie działa w grach z niedoskonałą informacją i ogólnie są one znacznie bardziej złożone do rozwiązania niż gry z doskonałą informacją. W podrozdziale 6.6 widzieliśmy, że gracz w częściowo obserwowalnej grze, takiej jak Kriegspiel, może stworzyć drzewo gry w przestrzeni stanów przekonań. Na tym drzewku widzieliśmy, że w niektórych przypadkach gracz może znaleźć sekwencję ruchów (strategię), która prowadzi do wymuszonego mata, niezależnie od tego, w jakim stanie zaczęliśmy i bez względu na to, jakiej strategii używa przeciwnik. Jednak techniki opisane w rozdziale 6 nie mogą powiedzieć graczowi, co ma zrobić, gdy nie ma zagwarantowanego mata. Jeśli najlepsza strategia gracza zależy od strategii przeciwnika i odwrotnie, to minimax (lub alfa-beta) sam w sobie nie może znaleźć rozwiązania. Rozbudowana forma pozwala nam znaleźć rozwiązania, ponieważ reprezentuje stany przekonań (teoretycy gier nazywają je zbiorami informacji) wszystkich graczy jednocześnie. Z tej reprezentacji możemy znaleźć rozwiązania równowagi, tak jak to zrobiliśmy w grach o postaci normalnej. Jako prosty przykład gry sekwencyjnej, umieść dwóch agentów w świecie 4×3 z rysunku wcześniejszym i pozwól im poruszać się jednocześnie, aż jeden agent dotrze do pola wyjściowego i otrzyma zapłatę za to pole. Jeśli określimy, że żaden ruch nie występuje, gdy dwaj agenci próbują jednocześnie wjechać na ten sam plac (powszechny problem na wielu skrzyżowaniach), wtedy pewne czyste strategie mogą utknąć na zawsze. Dlatego agenci potrzebują mieszanej strategii, aby dobrze radzić sobie w tej grze: losowo wybieraj między pójściem do przodu a pozostaniem w miejscu. Właśnie to robi się, aby rozwiązać kolizje pakietów w sieciach Ethernet. Następnie rozważymy bardzo prosty wariant pokera. Talia ma tylko cztery karty, dwa asy i dwa króle. Każdy gracz otrzymuje jedną kartę. Pierwszy gracz ma wtedy możliwość podniesienia stawki gry z 1 punktu do 2 lub przeczekania. Jeśli gracz 1 sprawdzi, gra się kończy. Jeśli gracz 1 przebije, wówczas gracz 2 może sprawdzić, akceptując, że gra jest warta 2 punkty, lub spasować, tracąc 1 punkt. Jeśli gra nie kończy się spasowaniem, wypłata zależy od kart: wynosi zero dla obu graczy, jeśli mają tę samą kartę; w przeciwnym razie gracz z królem płaci stawki graczowi z asem. Drzewo postaci ekstensywnej dla tej gry pokazano na rysunku. Gracz 0 to szansa; Gracze 1 i 2 są oznaczeni trójkątami. Każda akcja jest przedstawiona jako strzałka z etykietą, odpowiadającą podbiciu, zaczekaniu, sprawdzeniu lub spasowaniu, lub, w przypadku przypadku, czterem możliwym rozdaniom („AK” oznacza, że ​​gracz 1 otrzymuje asa, a gracz 2 króla). Stany końcowe to prostokąty oznaczone według ich wypłat dla gracza 1 i gracza 2. Zestawy informacji są pokazane jako oznaczone kreskowanymi polami; na przykład I1;1 to zestaw informacji, w którym jest tura gracza 1, a on wie, że ma asa (ale nie wie, co ma gracz 2). W zestawie informacji I2;1 jest tura gracza nr 2, który wie, że ma asa i że gracz nr 1 przebił, ale nie wie, jaką kartę ma gracz nr 1. (Ze względu na ograniczenia dwuwymiarowego papieru, ten zestaw informacji jest pokazany jako dwa pola, a nie jedno). Jednym ze sposobów rozwiązania rozbudowanej gry jest przekształcenie jej w grę w normalnej formie. Przypomnijmy, że forma normalna to macierz, której każdy wiersz jest oznaczony czystą strategią dla gracza 1, a każda kolumna czystą strategią dla gracza 2. W rozbudowanej grze czysta strategia dla gracza i odpowiada akcji dla każdego zestaw informacji dotyczących tego gracza. Tak więc na rysunku  jedną czystą strategią dla gracza 1 jest „podbicie, gdy mam I1;1 (to znaczy, kiedy mam asa) i czekanie, gdy mam I1;2 (kiedy mam króla)”. W poniższej macierzy wypłat strategia ta nazywa się rk. Podobnie strategia cf dla gracza 2 oznacza „sprawdzenie, gdy mam asa i spasowanie, gdy mam króla”. Ponieważ jest to gra o sumie zerowej, poniższa macierz daje tylko wypłatę dla gracza 1; gracz 2 zawsze ma odwrotną wypłatę:

Ta gra jest tak prosta, że ​​ma dwie czysto-strategiczne równowagi, zaznaczone pogrubioną czcionką: cf dla gracza 2 i rk lub kk dla gracza 1. Ogólnie jednak możemy rozwiązywać rozbudowane gry, konwertując do postaci normalnej, a następnie znajdując rozwiązanie (zazwyczaj strategia mieszana) przy użyciu standardowych metod programowania liniowego. To działa w teorii. Ale jeśli gracz ma zestawy informacji i akcje na zestaw, to będzie miał czyste strategie. Innymi słowy, rozmiar macierzy o postaci normalnej jest wykładniczy w liczbie zbiorów informacji, więc w praktyce podejście działa tylko w przypadku małych drzew gry – około tuzina stanów. Gra taka jak poker Texas hold’em dla dwóch graczy ma około 10¹⁸ stanów, co sprawia, że ​​takie podejście jest całkowicie niewykonalne. Jakie są alternatywy? W rozdziale 6 zobaczyliśmy, jak wyszukiwanie alfa-beta może obsługiwać gry z doskonałą informacją z ogromnymi drzewami łownymi poprzez przyrostowe generowanie drzewa, przycinanie niektórych gałęzi i heurystyczną ocenę węzłów nieterminalnych. Ale to podejście nie sprawdza się dobrze w grach z niedoskonałymi informacjami z dwóch powodów: po pierwsze, trudniej jest przycinać, ponieważ musimy rozważyć strategie mieszane, które łączą wiele gałęzi, a nie czystą strategię, która zawsze wybiera najlepszą gałąź. Po drugie, trudniej jest ocenić heurystycznie węzeł nieterminal, ponieważ mamy do czynienia ze zbiorami informacji, a nie z poszczególnymi stanami. Koller przyszedł na ratunek z alternatywną reprezentacją rozległych gier, zwaną formą sekwencji, która jest tylko liniowa w rozmiarze drzewa, a nie wykładnicza. Zamiast przedstawiać strategie, reprezentuje ścieżki przez drzewo; liczba ścieżek jest równa liczbie węzłów końcowych. W tej reprezentacji można ponownie zastosować standardowe metody programowania liniowego. Powstały system może rozwiązać warianty pokera z 25 000 stanami w minutę lub dwie. Jest to wykładnicze przyspieszenie w stosunku do podejścia z normalną formą, ale nadal jest dalekie od obsługi, powiedzmy, dwuosobowego Texas Hold’em z 10¹⁸ stanami. Jeśli nie możemy obsłużyć 10¹⁸ stanów, być może możemy uprościć problem, zmieniając grę na prostszą formę. Na przykład, jeśli mam asa i rozważam możliwość, że następna karta da mi parę asów, nie obchodzi mnie kolor następnej karty; zgodnie z zasadami pokera każdy kolor sprawdzi się równie dobrze. Sugeruje to tworzenie abstrakcji gry, w której kolory są ignorowane. Powstałe drzewo gry będzie mniejsze 4!=24. Załóżmy, że potrafię rozwiązać tę mniejszą grę; jak rozwiązanie tej gry będzie miało związek z oryginalną grą? Jeśli żaden gracz nie myśli o kolorze (jedynym rozdaniu, w którym liczą się kolory), to rozwiązanie abstrakcji będzie również rozwiązaniem dla oryginalnej gry. Jeśli jednak jakiś gracz rozważa kolor, to abstrakcja będzie tylko przybliżonym rozwiązaniem (ale możliwe jest obliczenie granic błędu). Istnieje wiele możliwości abstrakcji. Na przykład w momencie gry, w której każdy gracz ma dwie karty, jeśli mam parę dam, to ręce innych graczy mogą zostać podzielone na trzy klasy: lepiej (tylko para króli lub para asów) , to samo (para królowych) lub gorzej (wszystko inne). Jednak ta abstrakcja może być zbyt prostacka. Lepsza abstrakcja podzieliłaby gorzej na, powiedzmy, średnią parę (od dziewiątek do waletów), niską parę i brak pary. Te przykłady są abstrakcjami stanów; możliwe jest również abstrahowanie działań. Na przykład, zamiast mieć akcję zakładu dla każdej liczby całkowitej od 1 do 1000, możemy ograniczyć zakłady do 10⁰, 10¹, 10² i 10³. Albo możemy całkowicie wyciąć jedną z rund licytacji. Możemy również abstrahować od węzłów przypadkowych, biorąc pod uwagę tylko podzbiór możliwych transakcji. Jest to równoważne technice rollout używanej w programach Go. Łącząc wszystkie te abstrakcje, możemy zredukować 10¹⁸ stanów pokera do 10⁷ stanów, co jest wielkością, którą można rozwiązać za pomocą obecnych technik. W rozdziale 6 widzieliśmy, jak programy pokerowe, takie jak Libratus i DeepStack, były w stanie pokonać zwycięskich ludzkich graczy w heads-upie (dwóch graczy) w pokera Texas hold’em. Niedawno program Pluribus był w stanie pokonać ludzkich mistrzów w sześcioosobowym pokerze w dwóch formatach: pięć kopii programu przy stole z jednym człowiekiem i jedna kopia programu z pięcioma ludźmi. Mamy tu do czynienia z ogromnym skokiem złożoności. Z jednym przeciwnikiem jest możliwości ukrytych kart przeciwnika. Ale z pięcioma przeciwnikami jest 50wybrów10 ≈ 10 miliardów możliwości. Pluribus opracowuje podstawową strategię całkowicie na podstawie własnej gry, a następnie modyfikuje strategię podczas rzeczywistej gry, aby reagować na konkretną sytuację. Pluribus wykorzystuje kombinację technik, w tym wyszukiwanie drzewa Monte Carlo, wyszukiwanie z ograniczoną głębokością i abstrakcję. Forma rozbudowana jest wszechstronną reprezentacją: może obsługiwać częściowo obserwowalne, wieloagentowe, stochastyczne, sekwencyjne środowiska czasu rzeczywistego — większość trudnych przypadków z listy właściwości środowiska na stronie 61. Istnieją jednak dwa ograniczenia formy rozszerzonej w szczególności i ogólnie teorii gier. Po pierwsze, nie radzi sobie dobrze ze stanami i działaniami ciągłymi (chociaż istnieją pewne rozszerzenia przypadku ciągłego; na przykład teoria konkurencji Cournota wykorzystuje teorię gier do rozwiązywania problemów, w których dwie firmy wybierają ceny za swoje produkty z przestrzeni ciągłej ). Po drugie, teoria gier zakłada, że ​​gra jest znana. Niektóre części gry mogą być określone jako nieobserwowalne dla niektórych graczy, ale trzeba wiedzieć, które części są nieobserwowalne. W przypadkach, w których gracze poznają z czasem nieznaną strukturę gry, model zaczyna się załamywać. Zbadajmy każde źródło niepewności i czy każde z nich może być reprezentowane w teorii gier.

Akcje: Nie ma łatwego sposobu na przedstawienie gry, w której gracze muszą odkryć, jakie akcje są dostępne. Rozważ grę między twórcami wirusów komputerowych a ekspertami ds. bezpieczeństwa. Częścią problemu jest przewidywanie, jakie działania spróbują następnie podjąć twórcy wirusów.

Strategie: Teoria gier bardzo dobrze przedstawia ideę, że strategie innych graczy są początkowo nieznane – o ile zakładamy, że wszyscy agenci są racjonalni. Teoria nie mówi, co robić, gdy inni gracze nie są w pełni racjonalni. Pojęcie równowagi Bayesa-Nasha częściowo odnosi się do tego punktu: jest to równowaga w odniesieniu do wcześniejszego rozkładu prawdopodobieństwa gracza względem strategii innych graczy – innymi słowy, wyraża przekonania gracza na temat prawdopodobnych strategii innych graczy.

Szansa: Jeśli gra zależy od rzutu kostką, dość łatwo jest wymodelować węzeł losowy z równomiernym rozkładem wyników. Ale co, jeśli jest możliwe, że kostka jest niesprawiedliwa? Możemy przedstawić to z innym węzłem losowym, wyżej w drzewie, z dwiema gałęziami dla „kostka jest sprawiedliwa” i „kostka jest niesprawiedliwa”, tak że odpowiadające węzły w każdej gałęzi znajdują się w tym samym zbiorze informacji (czyli gracze nie wiedzą, czy kość jest sprawiedliwa, czy nie). A jeśli podejrzewamy, że przeciwnik wie? Następnie dodajemy kolejny węzeł szansy, z jedną gałęzią reprezentującą przypadek, w którym przeciwnik wie, i jedną, w której przeciwnik nie.

Narzędzia: Co jeśli nie znamy narzędzi przeciwnika? Ponownie, można to zamodelować za pomocą węzła losowego, tak aby drugi agent znał swoje własne narzędzia w każdej gałęzi, ale my nie. Ale co, jeśli nie znamy własnych narzędzi? Na przykład, skąd mam wiedzieć, czy rozsądnie jest zamówić sałatkę szefa kuchni, jeśli nie wiem, jak bardzo mi się spodoba? Możemy to wymodelować za pomocą kolejnego węzła losowego określającego nieobserwowalną „wewnętrzną jakość” sałatki. Widzimy zatem, że teoria gier jest dobra w przedstawianiu większości źródeł niepewności – ale kosztem podwojenia wielkości drzewa za każdym razem, gdy dodajemy kolejny węzeł; zwyczaj, który szybko prowadzi do nieprzyjemnie dużych drzew. Z powodu tych i innych problemów teoria gier była wykorzystywana głównie do analizy środowisk, które są w równowadze, a nie do kontrolowania agentów w środowisku.

Jednym z największych wyzwań, przed którymi stoi nasze społeczeństwo ze względu na rozwój technologii sztucznej inteligencji, jest zastąpienie ludzkich pracowników automatyzacją i narzędziami zrobotyzowanymi. Ponieważ jednak omawiane są problemy związane z AI, jednym z rzadko poruszanych tematów jest potencjał wprowadzenia przez te technologie nierównowagi między krajami. Rozwój technologii AI odbywa się w oszałamiającym tempie. Większość tego rozwoju na dużą skalę koncentruje się jednak w Stanach Zjednoczonych i Chinach, gdzie osiem największych firm AI (Google, Amazon, Facebook, Microsoft, IBM, Baidu, Tencent i Alibaba) ma swoje biura domowe. Dr Kai-Fu Lee, prezes Instytucji Sztucznej Inteligencji i prezes Sinovation Ventures, omawia to wyzwanie w artykule w “New York Times” pod tytułem “Prawdziwe zagrożenie sztuczną inteligencją”. Dr Lee twierdzi, że ponieważ każdy naród będzie potrzebował narzędzi sztucznej inteligencji, aby pozostać konkurencyjnym politycznie i gospodarczo, mniejsze lub biedniejsze kraje mogą być zmuszone do negocjowania umów z USA i Chinami w celu uzyskania potrzebnego im oprogramowania. Wskazuje również, że rządy wielu krajów mogą potrzebować pewnej formy powszechnego dochodu podstawowego lub dotacji, aby pomóc tym, którzy stracili pracę, automatyzacji, a także radzić sobie z utratą funduszy na podatek dochodowy od tych samych osób. Obserwacje dr Lee są wnikliwe i powinny służyć jako zachęta dla firm technologicznych i rządów do współpracy, ponieważ duże firmy technologiczne nie zawsze zdają sobie sprawę z wpływu, jaki ich narzędzia przyniosą na skalę społeczną lub globalną. Jednym potencjalnym rozwiązaniem globalnych dysproporcji w dostępności narzędzi sztucznej inteligencji byłoby oferowanie większej liczby programów, badań i danych AI “open source”, co oznacza, że byłyby dostępne dla każdego na całym świecie, co zachęcałoby do bardziej zrównoważonego i sprawiedliwego rozwoju.

Aby przedstawić gry stochastyczne, takie jak tryktrak, w rozbudowanej formie, dodajemy gracza o nazwie Szansa, którego wybory są określane przez rozkład prawdopodobieństwa. Reprezentując jednoczesne ruchy, jak w przypadku dylematu więźnia lub dwupalcowej Morry, narzucamy graczom dowolny rozkaz, ale mamy możliwość stwierdzenia, że działania wcześniejszego gracza nie są obserwowalne dla kolejnych graczy: np. Ali musi wybrać najpierw odmówić lub zeznać, potem Bo wybiera, ale Bo nie wie, jakiego wyboru dokonał Ali w tym czasie (możemy również przedstawić fakt, że ruch zostanie ujawniony później). Zakładamy jednak, że gracze zawsze pamiętają wszystkie swoje poprzednie działania; to założenie nazywa się doskonałym przypomnieniem.

W przeszłości rozpowszechnianie informacji przed ważnymi wyborami odbywało się głównie za pośrednictwem ulotek i plakatów. Dzisiaj tego rodzaju informacje są rozpowszechniane głównie w formie cyfrowej, przy użyciu zaawansowanych technologii, aby wpływać na opinie wyborców na bardziej osobistym poziomie. Dzięki ogromnej ilości danych dostępnych w serwisach takich jak Facebook, można zidentyfikować płeć, wiek i pochodzenie etniczne pochodzenie poszczególnych wyborców, a także ich hobby, a nawet niektóre z ich emocjonalnych doświadczeń. Tego rodzaju informacje mogą być wykorzystywane przez kandydatów politycznych jako podstawa do tworzenia spersonalizowanych komunikatów kampanii. Jedna brytyjska firma o nazwie Cambridge Analytica została oskarżona o wykorzystywanie technologii AI do niesprawiedliwego wpływu na wyniki wyborów prezydenckich w USA w 2016 r. Na swojej stronie internetowej firma stwierdza, że “wykorzystuje dane do zmiany zachowań odbiorców. Firma twierdzi również, że ma ponad 5000 punktów danych na temat ponad 230 milionów amerykańskich wyborców. Według strony scout.ai, Cambridge Analytica “wykorzystuje zautomatyzowaną manipulację emocjonalną wraz z rojami botów, ciemnymi postami na Facebooku, testami A / B i fałszywymi sieciami informacyjnymi, które stanowią prawie nieprzeniknioną maszynę do manipulacji wyborcami”. Usługi Cambridge Analytica były podobno również wykorzystywane w kampanii pro Brexit w Wielkiej Brytanii. Według Wikipedii firma jest obecnie przedmiotem dochodzeń kryminalnych zarówno w Stanach Zjednoczonych, jak i Wielkiej Brytanii. Rzekome przewinienie tej firmy jest tylko jednym przykładem tego, jak duże ilości danych, analizy danych i sztuczna inteligencja są wykorzystywane do wpływania na wybory polityczne. Często trudno jest wykryć wykorzystanie tego rodzaju programów i usług na arenie politycznej. Najwyraźniej jednak praktyki te budzą obawy natury etycznej, moralnej i prawnej. Dlatego w związku z dalszym rozwojem technologii należy wprowadzić zasady i przepisy dotyczące tych kwestii.

W ogólnym przypadku gra składa się z sekwencji tur, które nie muszą być takie same. Takie gry najlepiej reprezentuje drzewo gier, które teoretycy gier nazywają formą ekstensywną. Drzewo zawiera wszystkie te same informacje, które widzieliśmy w sekcji 6.1: stan początkowy S0, funkcję GRACZ(y), która mówi, który gracz ma ruch, funkcję AKCJE wyliczającą możliwe akcje, funkcję WYNIK(i;a) ), która definiuje przejście do nowego stanu, oraz funkcję częściową UTILITY(s; p), która jest zdefiniowana tylko w stanach terminalowych, aby dać wypłatę każdemu graczowi. Gry stochastyczne można uchwycić, wprowadzając wybitnego gracza, Chance, który może podejmować losowe akcje. „Strategia” Chance’a jest częścią definicji gry, określonej jako rozkład prawdopodobieństwa na działania (inni gracze mogą wybrać własną strategię). Aby reprezentować gry z niedeterministycznymi akcjami, takie jak bilard, dzielimy akcję na dwie części: sama akcja gracza ma deterministyczny skutek, a następnie Chance ma kolej, by zareagować na akcję na swój własny, kapryśny sposób. Na razie poczynimy jedno uproszczone założenie: zakładamy, że gracze mają doskonałe informacje. Z grubsza, doskonała informacja oznacza, że ​​kiedy gra wzywa ich do podjęcia decyzji, wiedzą dokładnie, gdzie się znajdują w drzewie gry: nie mają pewności co do tego, co wydarzyło się wcześniej w grze. Tak jest oczywiście w grach takich jak szachy czy Go, ale nie w grach takich jak poker czy Kriegspiel. W dalszej części pokażemy, jak rozbudowaną formę można wykorzystać do przechwytywania niedoskonałych informacji w grach, ale na razie założymy doskonałe informacje. Strategia w rozbudowanej grze zawierającej doskonałe informacje jest funkcją dla gracza, która dla każdego z jego stanów decyzyjnych określa, które działanie w AKCJACH gracz powinien wykonać. Gdy każdy gracz wybierze strategię, wynikowy profil strategii będzie śledzić ścieżkę w drzewie gry od stanu początkowego S0 do stanu terminala, a funkcja UTILITY definiuje narzędzia, które następnie otrzyma każdy gracz. Biorąc pod uwagę tę konfigurację, możemy bezpośrednio zastosować aparat równowagi Nasha, który wprowadziliśmy powyżej, do analizy gier w formie ekstensywnej. Aby obliczyć równowagi Nasha, możemy użyć prostego uogólnienia techniki wyszukiwania minimaksowego, którą widzieliśmy w rozdziale 6. W literaturze na temat gier w formie ekstensywnej technika ta nazywana jest indukcją wsteczną – widzieliśmy już indukcję wsteczną nieformalnie używaną do analizy skończonych powtarzający się dylemat więźnia. Indukcja wsteczna wykorzystuje programowanie dynamiczne, pracując wstecz od stanów terminalowych z powrotem do stanu początkowego, progresywnie oznaczając każdy stan profilem wypłat (przypisanie wypłat graczom), który zostałby uzyskany, gdyby gra była rozgrywana optymalnie od tego momentu. Bardziej szczegółowo, dla każdego nieterminalnego stanu s, jeśli wszystkie dzieci s zostały oznaczone profilem wypłat, to oznacza to profil wypłat ze stanu potomnego, który maksymalizuje wypłatę gracza podejmującego decyzję w stanie s. (Jeśli jest remis, wybierz arbitralnie; jeśli mamy węzły losowe, oblicz oczekiwaną użyteczność.) Algorytm indukcji wstecznej gwarantuje zakończenie działania, a ponadto działa w czasie wielomianu w rozmiarze drzewa gry. Gdy algorytm wykonuje swoją pracę, śledzi strategie dla każdego gracza. Jak się okazuje, strategie te są strategiami równowagi Nasha, a profil wypłat oznaczający stan początkowy jest profilem wypłaty, który można by uzyskać grając w strategie równowagi Nasha. Tak więc strategie równowagi Nasha dla gier o postaci ekstensywnej mogą być obliczane w czasie wielomianowym przy użyciu indukcji wstecznej; a ponieważ algorytm gwarantuje oznaczenie stanu początkowego profilem wypłaty, wynika z tego, że każda gra w formie ekstensywnej ma co najmniej jedną równowagę Nasha w czystych strategiach. Są to atrakcyjne wyniki, ale jest kilka zastrzeżeń. Drzewa gry bardzo szybko stają się bardzo duże, więc wielomianowy czas działania należy rozumieć w tym kontekście. Ale co bardziej problematyczne, sama równowaga Nasha ma pewne ograniczenia, gdy jest stosowana do gier w formie ekstensywnej. Rozważ grę z rysunku

Gracz 1 ma do dyspozycji dwa ruchy: powyżej lub poniżej. Jeśli porusza się poniżej, obaj gracze otrzymują wypłatę 0 (niezależnie od ruchu wybranego przez gracza 2). Jeśli porusza się w górę, gracz 2 ma do wyboru ruch w górę lub w dół: jeśli porusza się w dół, obaj gracze otrzymują wypłatę 0, a jeśli porusza się w górę, obaj otrzymują 1. Indukcja do tyłu natychmiast nam mówi. to (powyżej; w górę) jest równowagą Nasha, co powoduje, że obaj gracze otrzymują wypłatę w wysokości 1. Jednak (poniżej; w dół) jest również równowagą Nasha, w której obaj gracze otrzymują wypłatę 0.  Gracz 2 grozi graczowi 1, wskazując, że jeśli zostanie wezwany do podjęcia decyzji, wybierze przegraną, co skutkuje wypłatą 0 dla gracza 1; w tym przypadku gracz 1 nie ma lepszej alternatywy niż wybór poniżej. Problem polega na tym, że groźba gracza nr 2 (ogranie) nie jest wiarygodną groźbą, ponieważ jeśli gracz nr 2 jest rzeczywiście wezwany do dokonania wyboru, to dokona wyboru. Problem ten rozwiązuje udoskonalona równowaga Nasha, zwana idealną równowagą Nasha podgry. Aby to zdefiniować, potrzebujemy idei podgry. Każdy stan decyzyjny w podgrze drzewa gry (włącznie ze stanem początkowym) definiuje podgrę — gra na rysunku 17.4 zawiera zatem dwie podgry, jedną opartą na stanie decyzyjnym gracza 1, a drugą o stanie decyzyjnym gracza 2. Profil strategii tworzy następnie idealną równowagę Nasha dla podgry w grze G, jeśli jest to równowaga J-Nasha w każdej podgrze G. Stosując tę ​​definicję do gry z rysunku, stwierdzamy, że (powyżej) jest idealną podgry, ale (poniżej; w dół) nie jest, ponieważ wybieranie down nie jest równowagą Nasha podgry zakorzenioną w stanie decyzji gracza 2. Chociaż potrzebowaliśmy nowej terminologii, aby zdefiniować idealną równowagę Nasha w podgry, nie potrzebujemy żadnych nowych algorytmów. Strategie obliczone przez indukcję wsteczną będą idealną równowagą Nasha dla podgry, a wynika z tego, że każda gra o doskonałej formie w formie ekstensywnej ma idealną równowagę Nasha dla podgry, którą można obliczyć w wielomianu czasu w rozmiarze drzewa gry.

Oprócz Stanów Zjednoczonych i Chin, które są światowym liderem w dziedzinie rozwoju i wdrażania sztucznej inteligencji, istnieje wiele innych krajów, które zaczęły intensywnie inwestować w narzędzia AI. Kanada wprowadziła kilka innowacyjnych inicjatyw, które pozwolą na bardziej efektywne wykorzystanie AI w tym kraju. Z zadowoleniem przyjęła również napływ talentów w dziedzinie uczenia maszynowego i sztucznej inteligencji. Jednym z powodów migracji liderów technologii do Kanady jest Vector Institute, organizacja, która stara się zagłębić w aplikacje AI i zapewnić absolwentom głębszej edukacji więcej niż jakakolwiek inna instytucja na świecie. DeepMind firmy Alphabet, poprzednio prowadzony przez Google, otworzył swoje pierwsze międzynarodowe laboratorium badawcze w Edmonton w Kanadzie, gdzie dziedzinę głębokiego uczenia się stworzyli kanadyjscy naukowcy Geoffrey Hinton i Yoshua Bengio. Facebook ogłosił również, że otworzy laboratorium AI w Montrealu w Kanadzie, które początkowo zatrudni 10 badaczy sztucznej inteligencji. Krótko mówiąc, Kanada ma wszystkie elementy niezbędne do stania się supermocarstwem AI. W dziedzinie edukacji i zaawansowanych technologii Finlandia staje się również liderem w dziedzinie sztucznej inteligencji. Premier Juha Sipilä mówił już o swoim pragnieniu, aby kraj ten przewodził światu w tych technologiach. Jako niewielki, zdigitalizowany i innowacyjny kraj z tętniącym życiem środowiskiem dla startupów, Finlandia ma ogromny potencjał do globalnego przywództwa AI. Finlandia została wybrana przez IBM, światowego lidera w dziedzinie sztucznej inteligencji, do korzystania ze słynnego narzędzia sztucznej inteligencji firmy Watson w celu opracowania spersonalizowanej opieki zdrowotnej i pobudzenia wzrostu gospodarczego. Wiele innych krajów naśladuje przykłady tych wiodących krajów w świecie sztucznej inteligencji . W miarę jak rządy i organizacje będą coraz bardziej zainteresowane zastosowaniem AI, inne kraje prawdopodobnie pójdą w ich ślady.

Do tej pory przyglądaliśmy się tylko grom, które trwają jeden ruch. Najprostszym rodzajem gry z wieloma ruchami jest gra powtarzana (zwana również grą iterowaną), w której gracze wielokrotnie rozgrywają rundy gry z jednym ruchem, zwanej grą etapową. Strategia w powtarzanej grze określa wybór akcji dla każdego gracza w każdym kroku czasowym dla każdej możliwej historii poprzednich wyborów graczy. Najpierw spójrzmy na przypadek, w którym gra etapowa powtarza się o ustalonej, skończonej i wzajemnie znanej liczbie rund – wszystkie te warunki są wymagane, aby poniższa analiza zadziałała. Załóżmy, że Ali i Bo grają w powtórzoną wersję dylematu więźnia i oboje wiedzą, że muszą rozegrać dokładnie 100 rund gry. W każdej rundzie zostaną zapytani, czy mają zeznawać, czy odmówić, i otrzymają zapłatę za tę rundę zgodnie z zasadami dylematu więźnia, który widzieliśmy powyżej. Na koniec 100 rund obliczamy ogólną wypłatę dla każdego gracza, sumując wypłaty tego gracza w 100 rundach. Jakie strategie powinni wybrać Ali i Bo, aby zagrać w tę grę? Rozważ następujący argument. Oboje wiedzą, że setna runda nie będzie grą powtórzoną – to znaczy, że jej wynik nie może mieć wpływu na kolejne rundy. Tak więc w 100. rundzie grają w grę z dylematem jednego więźnia.

Jak widzieliśmy powyżej, wynik 100. rundy będzie (zeznaj; zeznaj) dominującą strategią równowagi dla obu graczy. Ale po ustaleniu setnej rundy, 99. runda może nie mieć wpływu na kolejne rundy, więc ona też ustąpi (zeznawać; zeznawać). Dzięki temu indukcyjnemu argumentowi obaj gracze wybiorą zeznania w każdej rundzie, za co otrzymają łącznie 500 lat więzienia. Ten rodzaj rozumowania jest znany jako indukcja wsteczna i odgrywa fundamentalną rolę w teorii gier. Jeśli jednak odrzucimy jeden z trzech warunków – ustalony, skończony lub wzajemnie znany – wtedy argument indukcyjny nie będzie słuszny. Załóżmy, że gra powtarza się nieskończoną liczbę razy. Matematycznie strategia dla gracza w nieskończenie powtarzanej grze to funkcja, która odwzorowuje każdą możliwą skończoną historię gry na wybór w grze etapowej dla tego gracza w odpowiedniej rundzie. W ten sposób strategia analizuje to, co wydarzyło się wcześniej w grze, i decyduje, jakiego wyboru dokonać w bieżącej rundzie. Ale nie możemy przechowywać nieskończonej tabeli w skończonym komputerze. Potrzebujemy skończonego modelu strategii dla gier, które będą rozgrywane w nieskończonej liczbie rund. Z tego powodu standardem jest przedstawianie strategii dla nieskończenie powtarzanych gier jako automatów skończonych (FSM) z wyjściem. Rysunek ilustruje szereg strategii FSM dla iterowanego dylematu więźnia.

Rozważ strategię Tit-za-Tat. Każdy owal jest stanem maszyny, a wewnątrz owalu znajduje się wybór, którego dokonałaby strategia, gdyby maszyna była w tym stanie. Z każdego stanu mamy jedną krawędź wychodzącą dla każdego możliwego wyboru agenta odpowiednika: podążamy za krawędzią wychodzącą odpowiadającą wyborowi dokonanemu przez drugą, aby znaleźć następny stan maszyny. Na koniec jeden stan jest oznaczony strzałką przychodzącą, wskazując, że jest to stan początkowy. Tak więc w przypadku TIT-FOR-TAT maszyna uruchamia się w stanie odpadu; jeśli przeciwnik zagra odmowę, pozostaje w stanie odmowy, natomiast jeśli przeciwnik zagra zeznaje, przechodzi do stanu zeznania. Pozostanie w stanie zeznań tak długo, jak jego odpowiednik będzie zeznawał, ale jeśli kiedykolwiek jego odpowiednik zagra odmowę, powróci do stanu odmowy. Podsumowując, TIT-FOR-TAT rozpocznie się od wybrania odmowy, a następnie po prostu skopiuje to, co jego odpowiednik zrobił w poprzedniej rundzie. Strategie HAWK i DOVE są prostsze: HAWK po prostu gra zeznania w każdej rundzie, podczas gdy DOVE po prostu gra odmowę w każdej rundzie. Strategia GRIM jest nieco podobna do TIT-FOR-TAT, ale z jedną ważną różnicą: jeśli kiedykolwiek jej odpowiednik zeznaje, to zasadniczo zamienia się w HAWK: gra zeznawanie w nieskończoność. Podczas gdy TIT-FOR-TAT jest wyrozumiały, w tym sensie, że zareaguje na późniejszą odmowę, odwzajemniając to samo, z GRIM nie ma odwrotu. Samo zagranie zeznaj raz spowoduje karę (zagranie zeznania), która trwa wiecznie. (Czy widzisz, co robi TAT-FOR-TIT?) Następnym problemem związanym z nieskończenie powtarzanymi grami jest to, jak zmierzyć użyteczność nieskończonej sekwencji wypłat. Tutaj skupimy się na podejściu do granicy średnich — zasadniczo oznacza to branie średniej z otrzymanych użyteczności w ciągu nieskończonego ciągu. Przy takim podejściu, mając nieskończoną sekwencję wypłat (U₀,U₁,U₂,…), definiujemy użyteczność sekwencji dla odpowiedniego gracza jako:

Nie można zagwarantować, że ta wartość będzie zbieżna dla dowolnych sekwencji użyteczności, ale jest to gwarantowane dla sekwencji użyteczności, które są generowane, jeśli używamy strategii FSM. Aby to zobaczyć, zauważ, że jeśli strategie FSM grają przeciwko sobie, to w końcu FSM ponownie wejdą w konfigurację, w której byli poprzednio, w którym to momencie zaczną się powtarzać. Dokładniej, każda sekwencja użyteczności wygenerowana przez strategie FSM będzie składać się ze skończonej (prawdopodobnie pustej) niepowtarzającej się sekwencji, po której następuje niepusta skończona sekwencja, która powtarza się nieskończenie często. Aby obliczyć średnią użyteczność otrzymaną przez gracza na tej nieskończonej sekwencji, musimy po prostu obliczyć średnią na skończonej powtarzającej się sekwencji. W dalszej części założymy, że gracze w nieskończenie powtarzanej grze po prostu wybierają maszynę skończonych stanów, aby zagrać w grę w ich imieniu. Nie nakładamy żadnych ograniczeń na te maszyny: mogą być tak duże i rozbudowane, jak chcą gracze. Gdy wszyscy gracze wybiorą maszynę skończonych stanów, aby grać w ich imieniu, możemy obliczyć wypłaty dla każdego gracza, korzystając z podejścia limitu środków, jak opisano powyżej. W ten sposób nieskończenie powtarzana gra sprowadza się do normalnej gry, aczkolwiek z nieskończenie wieloma możliwymi strategiami dla każdego gracza. Zobaczmy, co się stanie, gdy rozegramy nieskończenie powtarzający się dylemat więźnia, stosując strategie z rysunku. Po pierwsze, załóżmy, że Ali i Bo wybierają DOVE.

Nietrudno zauważyć, że ta para strategii nie tworzy równowagi Nasha: każdy z graczy zrobiłby lepiej, gdyby zmienił swój wybór na HAWK. Załóżmy więc, że Ali przełącza się na HAWK:

To najgorszy możliwy wynik dla Bo; i ta para strategii znowu nie jest równowagą Nasha. Bo zrobiłby lepiej, wybierając również HAWK:

Ta para strategii tworzy równowagę Nasha, ale niezbyt interesującą – zabiera nas mniej więcej do punktu, w którym zaczęliśmy w wersji gry z jednym strzałem, w której obaj gracze zeznają przeciwko sobie. Ilustruje kluczową właściwość nieskończenie powtarzanych gier: równowaga Nasha w grze scenicznej będzie utrzymywana jako równowaga w nieskończenie powtarzanej wersji gry. Jednak nasza historia jeszcze się nie skończyła. Załóżmy, że Bo przeszedł na GRIM:

Tutaj Bo nie robi gorzej niż gra w HAWK: w pierwszej rundzie Ali zeznaje, podczas gdy Bo gra odmawia, ale to skłania Bo do zeznawania na zawsze: utrata użyteczności w pierwszej rundzie znika w limicie. Ogólnie rzecz biorąc, obaj gracze otrzymują taką samą użyteczność, jak gdyby obaj grali w HAWK. Ale o to chodzi: te strategie nie tworzą równowagi Nasha, ponieważ tym razem Ali ma korzystne odchylenie – do GRIM. Jeśli obaj gracze wybiorą GRIM, dzieje się tak:

Wyniki i wypłaty są takie same, jak gdyby obaj gracze wybrali DOVE, ale w przeciwieństwie do tego, GRIM grający przeciwko GRIM tworzy równowagę Nasha, a Ali i Bo są w stanie racjonalnie osiągnąć wynik, który jest niemożliwy w jednorazowej wersji gra. Aby zobaczyć, że te strategie tworzą równowagę Nasha, załóżmy, ze względu na sprzeczność, że tak nie jest. Wtedy jeden gracz – załóżmy bez utraty ogólności, że to Ali – ma korzystne odchylenie, w postaci strategii FSM, która przyniosłaby wyższą wypłatę niż GRIM. Teraz w pewnym momencie ta strategia musiałaby zrobić coś innego niż GRIM – w przeciwnym razie uzyskałaby taką samą użyteczność. Więc w pewnym momencie musi grać zeznawać. Ale wtedy strategia GRIM Bo przeszłaby w tryb kary, stale zeznając w odpowiedzi. W tym momencie Ali byłaby skazana na wypłatę nie wyższą niż -5: gorszą niż -1, którą otrzymałaby wybierając GRIM. W ten sposób obaj gracze wybierający GRIM tworzą równowagę Nasha w nieskończenie powtarzającym się dylemacie więźnia, dając racjonalnie trwały wynik, który jest niemożliwy w jednorazowej wersji gry. Jest to przykład ogólnej klasy wyników zwanych ludowymi twierdzeniami Nasha, które charakteryzują wyniki, które mogą być podtrzymane przez równowagę Nasha w nieskończenie powtarzanych grach. Powiedzmy, że wartość bezpieczeństwa gracza jest najlepszą wypłatą, jaką gracz może zagwarantować. Zatem ogólna forma ludowych twierdzeń Nasha jest z grubsza taka, że ​​każdy wynik J, w którym każdy gracz otrzymuje przynajmniej swoją wartość bezpieczeństwa, może zostać utrzymany jako równowaga Nasha w nieskończenie powtarzanej grze. Strategie GRIM są kluczem do ludowych twierdzeń: wzajemna groźba kary, jeśli jakikolwiek agent nie odegra swojej roli w pożądanym wyniku, utrzymuje graczy w ryzach. Działa to jednak jako środek odstraszający tylko wtedy, gdy drugi gracz uważa, że ​​przyjąłeś tę strategię – a przynajmniej, że mogłeś ją przyjąć. Możemy również uzyskać różne rozwiązania, zmieniając agentów, a nie zmieniając zasady zaangażowania. Załóżmy, że agenci są skończonymi maszynami stanowymi o n stanach i grają w grę z m > n całkowitymi krokami. Agenci nie są zatem w stanie przedstawić liczby pozostałych kroków i muszą traktować ją jako nieznaną. Dlatego nie mogą dokonać indukcji wstecznej i mogą swobodnie dojść do korzystniejszej równowagi (odrzuć, odrzuć) w powtórzonym Dylemacie Więźnia. W tym przypadku ignorancja jest błogością – a raczej błogością jest przekonanie przeciwnika, że ​​jesteś ignorantem. Twój sukces w tych powtarzających się grach w dużej mierze zależy w znacznym stopniu od tego, czy inny gracz postrzega cię jako łobuza lub prostaka, a nie od twoich rzeczywistych cech.

Obecnie krajami o największej liczbie startupów AI i najbardziej zaawansowanymi badaniami AI są Stany Zjednoczone i Chiny. Od dawna Stany Zjednoczone przodują w dziedzinie sztucznej inteligencji, oferując niektóre z najczęściej używanych narzędzi sztucznej inteligencji, ponieważ są domem dla firm takich jak Google, Facebook, Amazon i innych gigantów technologicznych, którzy tworzą, rozwijają i stosują sztuczną inteligencję zasoby. Jednak Chiny obecnie dokładają wielkich starań, aby zająć pozycję Ameryki jako światowy lider w dziedzinie technologii sztucznej inteligencji i już zaczęły odnosić sukcesy w komercjalizacji narzędzi do rozpoznawania twarzy i innych zasobów sztucznej inteligencji. Według chińskiego rządu do roku 2025 przemysł AI powinien generować ponad 59 miliardów dolarów produkcji rocznie. Ponadto kraj aspiruje do bycia liderem technologii AI do 2030 r. Biorąc pod uwagę wysiłek włożony w rozwój sztucznej inteligencji zarówno przez sektor publiczny, jak i prywatny, jest wysoce prawdopodobne, że Chiny będą światowym liderem AI w 2030 r., A nawet wcześniej Co więcej, podczas gdy Chiny przeznaczają coraz więcej swoich zasobów na sztuczną inteligencję, Stany Zjednoczone ograniczają finansowanie nauki, dając Chinom jeszcze lepszą okazję do osiągnięcia swoich celów. Jeden raport, sporządzony przez Accenture PLC i Frontier Economics, ocenia, że Narzędzia AI mogą zwiększyć roczną stopę wzrostu w Chinach o 1,6 punktu procentowego do roku 2035 pod względem wartości dodanej brutto. Malcolm Frank, współautor książki “Co robić, gdy maszyny robią wszystko”, twierdzi, że Indie to kolejny kraj, który przyjmie wiodącą rolę w rewolucji sztucznej inteligencji, ponieważ jest gospodarzem wielu dużych firm technologicznych i oferuje dynamiczne środowisko dla startupów.