Inaczej patrzymy na gry kooperacyjne, jeśli założymy, że agenci mają wspólny cel. Na przykład, jeśli myślimy o agentach jako o pracownikach firmy, wówczas strategiczne względy związane z tworzeniem koalicji, którymi zajmuje się na przykład rdzeń, nie mają znaczenia. Zamiast tego możemy chcieć zorganizować siłę roboczą (agentów) w zespoły, aby zmaksymalizować ich ogólną produktywność. Mówiąc bardziej ogólnie, zadaniem jest znalezienie koalicji, która maksymalizuje dobrobyt społeczny systemu, definiowany jako suma wartości poszczególnych koalicji. Dobrobyt społeczny struktury koalicyjnej CS piszemy jako sw(CS), z następującą definicją:
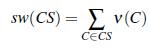
Wtedy optymalna społecznie struktura koalicyjna CS względem G maksymalizuje tę wielkość. Znalezienie społecznie optymalnej struktury koalicji jest bardzo naturalnym problemem obliczeniowym, który był badany poza społecznością systemów wieloagentowych: jest czasami nazywany problemem zbioru partycjonowania. Niestety problem jest NP-trudny, ponieważ liczba możliwych struktur koalicyjnych rośnie wykładniczo w liczbie graczy. Znalezienie optymalnej struktury koalicji poprzez naiwne, wyczerpujące poszukiwania jest zatem generalnie niewykonalne. Wpływowe podejście do optymalnego kształtowania struktury koalicji opiera się na idei poszukiwania podprzestrzeni grafu struktury koalicji. Pomysł najlepiej wyjaśnić na przykładzie. Załóżmy, że mamy grę z czterema agentami, N = {1,2,3,4}. Istnieje piętnaście możliwych struktur koalicyjnych dla tego zestawu agentów. Możemy zorganizować je w wykres struktury koalicji, jak pokazano na rysunku, gdzie węzły na poziomie ` wykresu odpowiadają wszystkim strukturom koalicji z dokładnie l koalicjami.
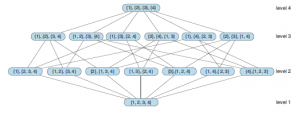
Górna krawędź na wykresie reprezentuje podział koalicji w dolnym węźle na dwie oddzielne koalicje w górnym węźle.
Na przykład istnieje przewaga od {{1},{2,3,4}} do {{1},{2},{3,4}}, ponieważ ta ostatnia struktura koalicji jest uzyskiwana z pierwszej poprzez podział koalicji {2,3,4} na koalicje {2} i {3,4} . Optymalna struktura koalicji CS leży gdzieś w grafie struktury koalicji, więc aby ją znaleźć, wydaje się, że musielibyśmy ocenić każdy węzeł na wykresie. Rozważmy jednak dwa dolne rzędy wykresu – poziomy 1 i 2. Każda możliwa koalicja (oprócz koalicji pustej) pojawia się na tych dwóch poziomach. (Oczywiście nie każda możliwa struktura koalicji pojawia się na tych dwóch poziomach.) Załóżmy teraz, że ograniczamy nasze poszukiwania możliwej struktury koalicji tylko do tych dwóch poziomów – nie idziemy wyżej na wykresie. Niech CS* będzie najlepszą strukturą koalicyjną, jaką znajdziemy na tych dwóch poziomach, a CS będzie najlepszą strukturą koalicyjną w ogóle. Niech C* będzie koalicją o największej wartości spośród wszystkich możliwych koalicji:
![]()
Wartość najlepszej struktury koalicji, którą znajdujemy na pierwszych dwóch poziomach wykresu struktury koalicji, musi być co najmniej równa wartości najlepszej możliwej koalicji: sw(CSl) ≥ v(C*). Dzieje się tak dlatego, że każda możliwa koalicja pojawia się w co najmniej jednej strukturze koalicyjnej na pierwszych dwóch poziomach wykresu. Załóżmy więc najgorszy przypadek, czyli sw(CS’) = v(C*). Porównaj wartość sw(CS’) z sw(CS*). Ponieważ sw(CS’) jest najwyższą możliwą wartością dowolnej struktury koalicyjnej, a istnieje n agentów (n = 4 w przypadku rysunku powyżej), to najwyższa możliwa wartość sw(CS*) będzie wynosić nv(C*) = n · sw(CS’). Innymi słowy, w najgorszym możliwym przypadku wartość najlepszej struktury koalicyjnej, jaką znajdziemy na pierwszych dwóch poziomach wykresu, wynosiłaby 1/n wartości najlepszej, gdzie n to liczba agentów. Tak więc, chociaż przeszukiwanie pierwszych dwóch poziomów wykresu nie gwarantuje uzyskania optymalnej struktury koalicji, gwarantuje uzyskanie takiej, która nie jest gorsza niż 1/n optymalnej. W praktyce często będzie znacznie lepiej.