Opiszemy teraz jeden schemat reprezentacji, zwany sieciami wkładu marginalnego (MC-nets). Posłużymy się nieco uproszczoną wersją, aby ułatwić prezentację, a uproszczenie sprawia, że jest niekompletna – pełna wersja MC-netów jest pełną reprezentacją. Ideą sieci wkładów krańcowych jest przedstawienie funkcji charakterystycznej gry (N,v) jako zbioru reguł koalicji wartości w postaci: (Ci,xi), gdzie Ci ⊆ N jest koalicją, a xi jest liczbą. Aby obliczyć wartość koalicji C, po prostu sumujemy wartości wszystkich reguł (Ci,xi) takich, że Ci ⊆ C. Zatem, mając dany zbiór reguł R = {(C1,x1),…,(Ck,xk}, odpowiadającą funkcją charakterystyczną jest:
![]()
Załóżmy, że mamy zestaw reguł R zawierający następujące trzy reguły:
{({1,2}.5), ({2},2) , ({3},3)}:
Wtedy na przykład mamy:
- v({1}) = 0 (ponieważ nie obowiązują żadne reguły),
- v({3}) = 4 (trzecia zasada),
- v({1.3}) = 4 (trzecia zasada),
- v({2.3}) = 6 (druga i trzecia zasada), oraz
- v({1,2,3}) = 11 (pierwsza, druga i trzecia zasada).
Dzięki tej reprezentacji możemy obliczyć wartość Shapleya w czasie wielomianowym. Kluczowym spostrzeżeniem jest to, że każdą regułę można rozumieć jako samodzielną definicję gry, w której gracze są symetryczni. Odwołując się do aksjomatów addytywności i symetrii Shapleya, wartość Shapleya φi(R) gracza i w grze związanej ze zbiorem reguł R jest zatem po prostu:
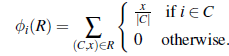
Przedstawiona przez nas wersja sieci wkładów krańcowych nie jest pełnym schematem reprezentacji: istnieją gry, których funkcji charakterystycznej nie można przedstawić za pomocą zestawów reguł o opisanej powyżej formie. Bogatszy typ sieci wkładów krańcowych dopuszcza reguły postaci (φ,x), gdzie φ jest formułą logiki zdań nad graczami N: koalicja C spełnia warunek φ, jeśli odpowiada satysfakcjonującemu przypisaniu dla φ . Ten schemat jest pełną reprezentacją – w najgorszym przypadku potrzebujemy reguły dla każdej możliwej koalicji. Co więcej, wartość Shapleya można obliczyć w czasie wielomianowym za pomocą tego schematu; szczegóły są bardziej skomplikowane niż w przypadku prostych zasad opisanych powyżej, chociaż podstawowa zasada jest taka sama.